Численное и экспериментальное моделирование течения в отсасывающей трубе гидротурбины

В настоящее время на гидроэнергетику приходится 87 % энергии, производимой из возобновляемых источников, на основе которых, в свою очередь, производят одну пятую всей энергии, потребляемой в мире [1]. Повышение устойчивости работы, увеличение КПД гидроэлектростанций невозможны без изучения физических механизмов гидродинамических процессов, имеющих место в проточных частях гидротурбин [2]. Существенную роль среди таких процессов играют нестационарные явления, связанные с образованием крупномасштабных вихревых структур. Одним из механизмов генерации пульсаций потока служит прецессия вихревого жгута [3], образующегося за рабочим колесом гидротурбины в режимах недогрузки или перегрузки работы гидротурбины, когда поток после прохождения через гидротурбину имеет достаточно большую остаточную закрутку. Для прогнозирования резонансных явлений, поис-

ка методов подавления неустойчивости необходима детальная информация о характеристиках и структуре потока.

Проведение детальных исследований на натурных ГЭС представляет большую сложность. Выходом может быть применение методов математического (численного) и экспериментально -го моделирования с использованием лабораторных установок. В контексте сказанного выше целью данной работы стало численное и экспериментальное исследование структуры течения в модельной отсасывающей трубе гидротурбины. Основной упор сделан на выявление особенностей течения, прежде всего, наличия интенсивных пульсаций и неравномерности потока. Экспериментальные исследования проводили с использованием замкнутого гидродинамического контура с максимальным расходом до 100-150 м3/ч. На данном этапе исследования вихревого течения, возникающего в отсасывающей трубе гидротурбины, проводили с использованием рабочего участка, моделирующего геометрию “TURBINE-99”. Эта геометрия, которую применяют для тестирования численных моделей течения в отсасывающих трубах гидротурбин [4], также хорошо адаптирована к оптическим методам исследования потока. В ходе опытов с использованием цифровой камеры и ЛДА были получены данные по визуализации потока и полям скоростей в различных сечениях отсасывающей трубы. Экспериментальные данные использованы для тестирования результатов численного моделирования. Было продемонстрировано хорошее соответствие измерений и расчетов.

Экспериментальная техника

Стенд представляет собой замкнутый гидравлический контур (рис. 1), состоящий из центробежного химического насоса Х100-80-160Т153 номинальной производительностью 100 м3/ч и напором 3,2 атм. с двигателем 22 кВт, баком емкостью 500 л и собственно рабочего участка (модели отсасывающей трубы). Для снижения потерь давления контур выполнен так, что в нем установлено всего два поворотных колена. Соединения частей контура (трубы, отводы, повороты, краны) выполнены с применением стандартной трубопроводной арматуры из полиэтиле-

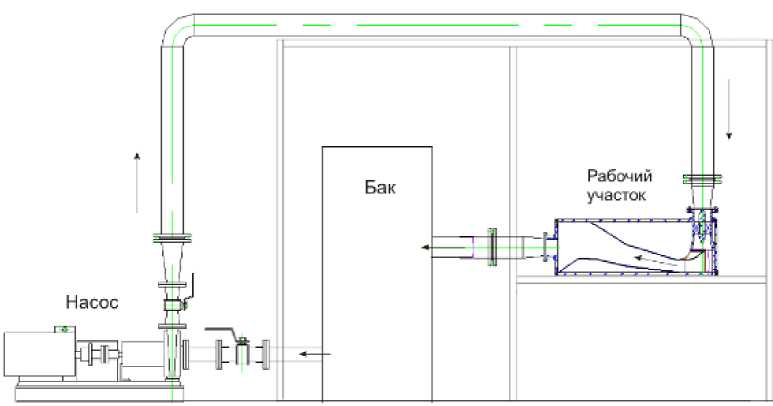
Рис.1. Схема экспериментального участка на (ПЭ80, ПЭ100). Регулирование расхода осуществляется регулированием частоты вращения вала с помощью частотного преобразователя (ЧП) ВЕСПЕР E2-8300-030H 22 кВт 380В. Для измерения расхода воды используется ультразвуковой расходомер с электронным блоком US – 800 – 11. Паспортная погрешность измерения расхода в рабочем диапазоне для данного стенда составляет не более 1 %.

В качестве модельной геометрии отсасывающей трубы выбрана конфигурация, использованная в проекте TURBINE-99 [4]. Модельный рабочий участок был выполнен целиком из органического стекла, что дает возможность полного оптического доступа ко всему полю течения во всех частях канала и, соответственно, широкого применения оптических бесконтактных методов для изучения характеристик течения. Конструкция рабочего участка, состоящего из сменных частей, позволяет также оперативно изменять внутреннюю геометрию канала. На входе в рабочий участок находится стационарный лопаточный завихритель с конструктивным параметром крутки S=0.4. Параметр крутки определен по геометрическим параметрам завихрителя [5]:

5 =

2 ( 1 - ( d 1/ d ₂ ) ³ )

3 [ ( 1 - ( d , / d ₂ ) ² ) )

tan ( ^ ) , где d i и d₂ - меньший и больший диаметры кольцевого канала

завихрителя (рис. 2), φ – угол наклона лопаток. Значение параметра крутки в нашей модели, равное, как и в прототипе TURBINE-99, 0,4, соответствует условиям работы натурных турбин. Приведенные в данной статье результаты были получены при достаточно большом числе Рейнольдса Re^HO5.

Визуализация потока в модели отсасывающей трубы осуществляется с помощью подсветки мелких пузырьков воздуха, подаваемого на вход центробежного насоса. Размеры и концентрация воздушных пузырьков могут регулироваться изменением подачи воздуха, а также варьированием оборотов двигателя насоса и расходом жидкости через байпасную линию. За счет границы межфазного раздела пузыри воздуха хорошо отражают свет и поэтому дают яркий, хорошо видимый трек. В качестве источника света используется 3Вт непрерывный твердо-

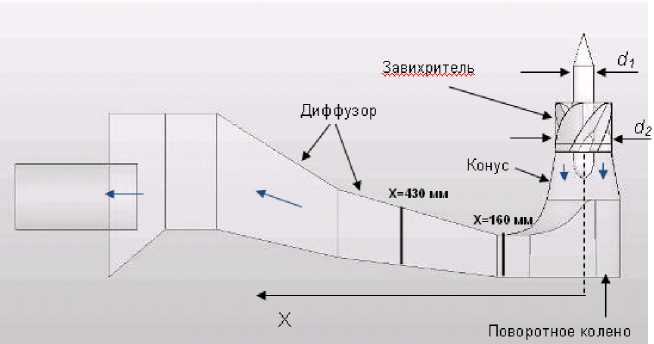
Рис. 2. Геометрия модельной трубы TURBINE-99. Закрутка потока в завихрителе производится по часовой стрелке, если смотреть сверху

тельный лазер с диодной накачкой KLM-532/h-3000. Луч лазера преобразовывается с помощью цилиндрической линзы в тонкий световой нож для визуализации течения в выбранном сечении. Регистрация картины течения производилась с помощью цифровой камеры CANON EOS 20D. Для съемки нестационарных процессов использовали скоростные камеры Видео Спринт и PCO 1200hs.

Измеряли локальные скорости с помощью автоматизированной системы ЛДА ЛАД-05 производства ИТ СО РАН. Оптическая система установлена на программно-управляемое 3-координатное перемещающее устройство, позволяющее позиционировать измерительный объем ЛДА по трем координатам с точностью до 12 мкм. Погрешность измерения средней скорости составляет не более 0,5 %.

Расчетная методика

Для сопоставления экспериментальных данных, полученных на стенде ИТ СО РАН, проведена серия расчетов с целью тестирования и адаптации расчетной модели.

Согласно современным представлениям трехмерные нестационарные течения вязкой жидкости описываются системой уравнений Навье-Стокса, состоящей из уравнения сохранения массы или уравнения неразрывности:

+v ( р v ) = о,                                                                   (1)

5t и уравнений движения или закона сохранения импульса:

г о v

+ V ( p v ■ v ) = -V p + V ( t ) + F ,                                               (2)

t где v – вектор скорости жидкости, τ – тензор вязких напряжений, F – вектор объемных сил, р – статическое давление, ρ – плотность.

Составляющие тензора вязких напряжений τ _ij определяются как

т

τ _ij

= И

d u i о u j 2 о u k

1 X^ ⁺ a X " ~3   d x

V Ji             k J где μ – динамическая (молекулярная) вязкость, ui – компоненты вектора скорости, δij – символ Кронекера.

Считается, что при помощи уравнения Навье-Стокса можно описать как ламинарное, так и турбулентное течение, однако на сегодня возможности существующей вычислительной техники таковы, что практически все реальные достижения в расчетах турбулентных течений связаны с использованием полуэмпирических моделей турбулентности, использующих подход Рейнольдса. Суть этого подхода заключается в решении осредненных уравнений Навье-Стокса [6,7]:

Р- + v( р v ■ v ) = -Vp + V(t - pv' ■ v') + F, где v - усредненное по времени поле скоростей, -рv' ■ v' - тензор рейнольдсовых напряжений.

При построении двухпараметрических моделей турбулентности для определения компонент тензора рейнольдсовых напряжений используют гипотезу Буссинеска о изотропной турбулентной вязкости:

- p v- v = ^t

dXj   dXj

V j 1 )

-

2 ( , — pk

³ V

du | ,

+        154

8xi)

где μ t – турбулентная вязкость, k – кинетическая энергия турбулентных пульсаций.

Использование концепции Буссинеска позволяет построить целый ряд двухпараметрических полуэмпирических моделей. В данной работе для замыкания системы RANS уравнений применялась двухзонная двухпараметрическая модель Ментера SST.

Модель Ментера записывается путем суперпозиции моделей k- ε и k- ω , основанной на том, что модели типа k- s лучше описывают свойства свободных сдвиговых течений, а модели k- to имеют преимущество при моделировании пристеночных течений. Плавный переход от k- to модели в пристеночной области к k- s модели вдали от твердых стенок обеспечивается введением весовой эмпирической функции F 1 . Вторая важная деталь модели состоит в изменении стандартной связи между k, ω и турбулентной вязкостью. Модификация этой связи состоит во введении перехода к формуле Бредшоу в пристеночной области. Согласно предположению Бредшоу напряжение сдвига в пограничном слое пропорционально энергии турбулентных пульсаций.

Ниже приведены основные уравнения M-SST модели [7]:

дрк     (      )     () P *

∂ρω                            P1

----+ V ( р v • to ) = V((p + CT_mp_t ) -Vro ) + YP--вР® 2 + (1 - F1) • (2 P^CT_m 2 — V k - Vro)'

∂t                                  µt

В члене генерации турбулентной энергии введен ограничитель:

P = T_y^du- P = min( P ,20 • вP®k ) • ∂x_j

Весовая функция и ее аргумент:

F ₁= tanh(arg₁)

arg1 = min(max(

k ^1,2 500 ^ . 4 P<7_m 2 k ’

*,        2);            2)

βωy ρωy CDkωy где положительная часть перекрестных диффузионных членов в уравнении переноса to:

CD k _m = max(2 Р^_т 2 -V k -V ^ ; 10 "' ) . ^ω

ρak

Выражения для вихревой вязкости с учетом гипотезы Бредшоу: ^t =------"-----, max(a1ω; F2Ω)

где величина завихренности - О = 2^ i ^il. .

Функция переключения F 2 определяется подобно F 1 :

F 2 = tanh(arg₂²)

k1,2   500^ • arg2 = max(2——,----r)

в toy pay

Константы в уравнениях переноса записывают путем суперпозиции констант для модели k-ω модели (Wilcox) и констант стандартной k-ε модели:

ф = Ф1F + Ф2(1 -F) ф Г. ,ае,у, в}.

Набор констант для пристеночного слоя SST модели: а_к 1 = 0.85 у_{ш 1} = 0.5 р 1 = 0.075 в _=К .

' в в!

Набор констант для свободных сдвиговых слоев: ст_{к 2} = 1.0 ст_{т 2} = 0.856 р ₂ = 0.0828 вх ^.^К /     ^*

в  м^

Другие константы, использующиеся в модели: в* = 0.09 ^К = 0.41 а 1 = 0.31.

При моделировании течений в гидротурбинах интерес представляет поведение не только осредненных характеристик течения, но и пульсационных (интенсивность пульсаций и частота). Получившее широкое распространение в инженерных расчетах URANS модели турбулентности занижают турбулентные пульсации в закрученном потоке. Чтобы улучшить моделирование нестационарных турбулентных закрученных течений, используют вихреразрешающие методы, как, например, метод моделирования крупных вихрей (Large Eddy Simulation – LES). Однако его применение требует очень детальной сетки, особенно вблизи стенок. В то же время RANS модели достаточно экономичны и хорошо описывают пограничные слои. Чтобы соединить достоинства этих подходов в работе [8], был предложен метод моделирования отсоединенных вихрей (DES). Первая версия DES базировалась на модели Спаларта-Алмароса. В дальнейшем метод DES стал использоваться с другими моделями турбулентности, появились различные его модификации.

Метод DES сочетает подходы RANS и LES. В областях потока, где размер вычислительной сетки А достаточен для разрешения энергонесущих вихрей, т.е. при А < L t , применяется метод LES, а в остальной области – RANS. Первая версия DES базировалась на модели Спаларта-Алмароса SA, в которой в качестве характерного линейного масштаба турбулентности используется расстояние до стенки d . При моделировании отсоединенных вихрей этот масштаб заменяется функцией:

d = mind, cdes A), где Cdes - эмпирическая константа, а А определяется как максимальный из трех размеров контрольного объема Δx, Δy, Δz. Таким образом, в пограничных слоях работают RANS модели, а в остальной области – LES.

Таким образом, для моделирования нестационарного турбулентного течения в данной работе использовали метод DES, основанный на на к -и SST модели Ментера и ограничении турбулентной вязкости: цt = ^JF^ , F des = max ( Lt^ C des ^a ) ,1 ) , L_t = k³'²I^е, c des = ^0,61.

Метод DES позволяет рассмотреть крупномасштабные турбулентные пульсации во всем проточном тракте гидротурбины и оценить их амплитудно-частотные характеристики.

Для аппроксимации конвективных членов уравнений гидродинамики взята схема QUICK – второго порядка точности. Аппроксимация нестационарного члена при URANS и DES моделирования проводилась неявной схемой второго порядка. Величина временного шага при этом удовлетворяла условию CFL < 2.

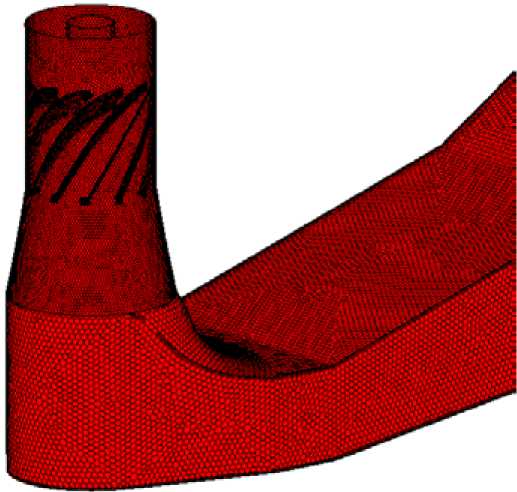
Рис. 3. Фрагмент расчетной сетки

Геометрия расчетной области показана на рис. 2. В качестве граничных условий на входе задавали фиксированный расход воды, равный 13 кг/с. Уровень турбулентных пульсаций на входе равнялся 1 %, характерный масштаб турбулентности 0,1 м. На выходе задавались условия фиксированного давления. Закрутка потока в эксперименте обеспечивалась завихрителем, состоящим из 12 лопастей, наклоненных под углом 30 градусов к оси обтекателя.

Для расчета использовалась неструктурированная сетка, состоящая из 420000 полигран-ных ячеек (рис. 3). Данный вид ячейки сочетает в себе высокую точность и быстродействие структурированных шестигранных ячеек и, подобно четырехгранным ячейкам, легко описывает любую сложную геометрию.

Результаты исследований

Качественные особенности течения в модели отсасывающей трубы были исследованы с помощью техники визуализации. На рисунке 2 показаны положения поперечных плоскостей визуализации. На рисунке 4 приведена визуализация потока в продольном центральном сечении в эксперименте и расчете. Как видно из рисунков, особенностью течения является формирование в поворотной части канала крупномасштабного вихря с горизонтальной осью. Можно увидеть также наличие в конической части выраженной приосевой и пристенных струй, направленных вниз. Особенностью течения выступает также неравномерность течения в диффузоре отсасывающей трубы (за поворотной частью), как видно из визуализации потока в продольных сечениях (рис. 5). Вдоль левой стенки наблюдается выраженный интенсивный проток жидкости в сторону выхода (рис. 5б), в то время как вдоль правой стенки видно хаотичное турбулизированное движение со слабым средним потоком в направлении выхода (рис. 5а). На основе анализа данных скоростной видеосъемки в поперечных сечениях можно также гово- – 495 –

а)

б)

Рис. 4. Визуализация течения в продольном центральном сечении трубы: а) экспериментальное; б) расчетное поле скорости рить об отсутствии в конической части отсасывающей трубы выраженного прецессирующего вихревого ядра. Отсутствие выраженной несимметрии мгновенного поля течения в поперечном сечении, характерной для закрученных потоков с прецессирующим вихревым ядром [6], можно видеть на рис. 6.

Количественные данные о поле течения были получены с помощью ЛДА системы. Радиальные профили двух компонент скоростей, измеренные и рассчитанные в поперечном сечении за обтекателем завихрителя, приведены на рис. 7-8. Профиль осевой скорости (рис. 8),

а)

б)

Рис. 5. (а) – визуализация течения в продольном сечении вдоль правой стенки (вид со стороны правой стенки); (б) – визуализация течения в продольном сечении вдоль левой стенки (вид со стороны левой стенки).

направленной вниз, демонстрирует наличие центральной и пристенной кольцевых струй на входе. Разделение потока на две кольцевые струи отражается также в форме профиля окружной компоненты скорости (рис. 8). Профиль радиальной скорости показывает, что центральная кольцевая струя за телом обтекания имеет тенденцию сужения. Внешняя кольцевая струя при этом расширяется, следуя вдоль стенки расширяющегося конуса. Спектральный анализ сигнала ЛДА при измерениях в области конической части канала не выявил определенной – 497 –

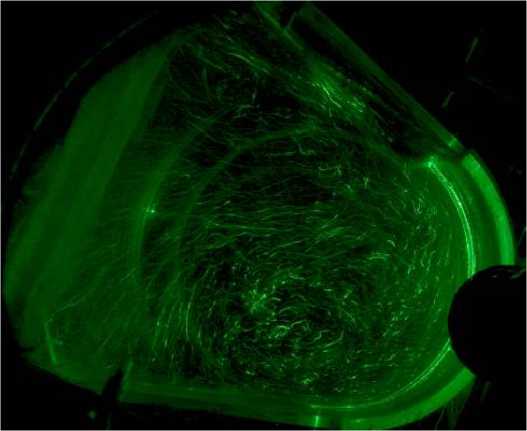
а)

б

Рис. 6. Визуализация течения в поперечном сечении под обтекателем: а) экспериментальное; б) расчетное поле скорости дискретной частоты, которая обычно выделяется в потоке с прецессирующим вихрем [9]. Этот факт подтверждает результат, полученный на основе визуальных наблюдений, об отсутствии прецессии вихревого жгута в нашей установке.

Как видно из графиков на рис.7-8, расчетная и экспериментальная формы обоих профилей скорости в данном сечении качественно и количественно хорошо согласуются. Вместе с тем есть и некоторые расхождения, вызванные сложностью экспериментальных измерений в диф- – 498 –

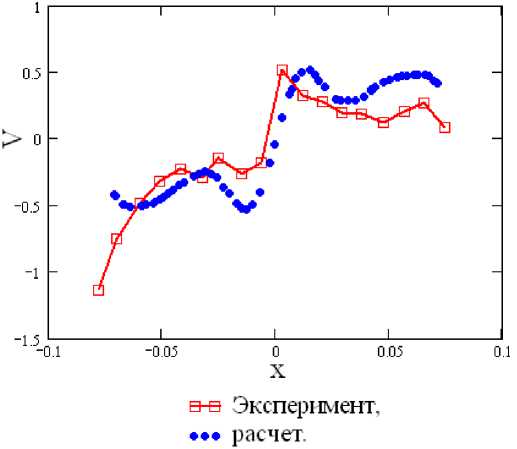
Рис. 7. Профиль тангенциальной скорости под телом обтекания

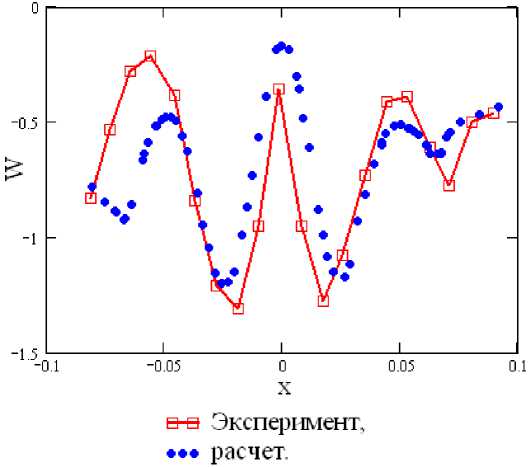
Рис. 8. Профиль осевой скорости под телом обтекания фузоре отсасывающей трубы и проявляющиеся в небольшой асимметрии экспериментальных профилей скорости. Тем не менее, для такой сложной задачи степень совпадения расчета и эксперимента можно считать достаточно хорошей.

Положение измерительного сечения для поля течения в диффузорной части показаны на рис. 2, а на рис. 9 приведены изолинии продольной скорости, обезразмеренной посредством среднерасходной скорости в сечении канала X=430 мм, полученные в эксперименте, и расчет.

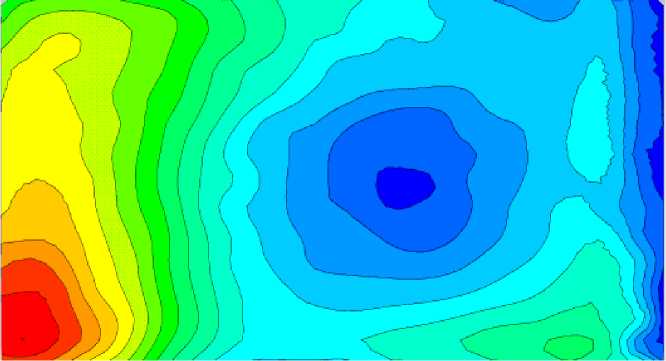
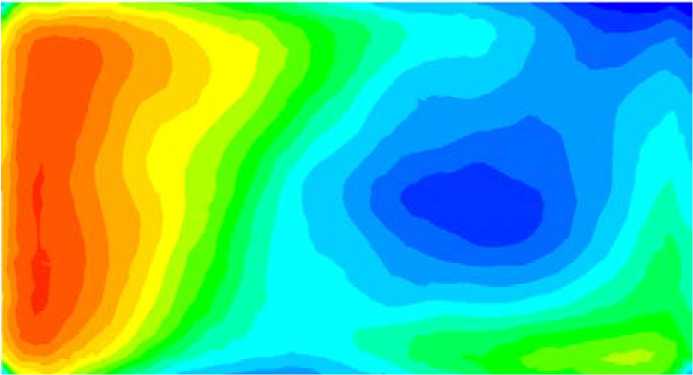
б)

Рис. 9. Изолинии безразмерной продольной компоненты скорости в сечении X=430 мм, обезразмеривание произведено через среднерасходную скорость для сечения X=430 мм 0.4 м/с: а) экспериментальные изолинии; б) расчетные изолинии

Измерения производили с шагом 10 мм при расходе 13 л/c, соответствующем числу Рейнольдса порядка 105. Как показывает анализ результатов, особенностью течения является выраженная неравномерность потока в горловине выхода из поворотного колена. Имеется интенсивный проток в левом нижнем углу (если смотреть в сторону выхода), а большая часть сечения занята медленным потоком. Положение области минимума примерно совпадает с центром крупномасштабного вихря, видного на картине течения, полученной на основе визуализации. Далее к выходу неравномерность сглаживается, но, тем не менее, остается заметной. Выявленная силь-– 500 – ная неравномерность течения в диффузоре, очевидно, приводит к дополнительным потерям энергии, снижающим эффективность работы отсасывающей трубы.

В расчете наблюдается аналогичная структура течения. В этом можно убедиться из сопоставления экспериментальной и расчетной картин течения в различных сечениях, приведенных на рис. 4, 6, 9. Как видно, структура течения в расчете качественно хорошо согласуется с экспериментом. Также наблюдается ярко выраженная неравномерность потока в поворотном колене. Имеется интенсивный проток в левом нижнем углу трубы. Примерно совпадают положения центров крупномасштабного вихря.

Заключение

Таким образом, в данной работе было проведено экспериментальное и численное исследование структуры течения в модельной геометрии отсасывающей трубы гидротурбины (TURBINE-99). Полученные результаты позволяют сделать ряд выводов об особенностях течения в модели данной конфигурации.

Наиболее интересным результатом является то, что в наших исследованиях при данных входных параметрах с завихрителем S=0.4 и при данном расходном режиме, соответствующем турбулентному режиму течения, не образуется выраженное прецессирующее вихревое ядро и не наблюдаются связанные с ним сильные пульсации потока. Этот факт был подтвержден на основе визуальных исследований с использованием скоростной камеры, а также на основе спектрального анализа ЛДА сигнала. Нужно отметить, что в предыдущих исследованиях для аналогичной конфигурации TURBINE-99 и той же степени закрутки потока прецессия вихревого жгута была зафиксирована в расчетах и эксперименте [4, 6]. Отсутствие прецессии вихревого ядра в нашей работе можно объяснить конструкцией использованного завихрителя, формирующего специфичный профиль осевой скорости на входе в конус отсасывающей трубы. Прецессия вихря всегда сопровождается зоной возвратного осевого течения под телом обтекания, однако наши входные условия формируют центральную приосевую струю, препятствующую образованию центральной рециркуляционной зоны. В работе [10] показано, что струя воды, испускаемая из отверстия на центральном теле обтекания, может полностью подавить прецессию вихревого ядра. Особенностью нашей работы является то, что устойчивый режим течения без образования прецессии вихря в отсасывающей трубе был получен без использования отдельного канала для подачи воды. Предполагается, что этот результат даст возможность для разработки рекомендаций по конструкции гидротурбины, не генерирующей мощные пульсации потока в отсасывающей трубе.

Еще одной особенностью течения было наличие крупномасштабных вихрей в области выхода из конуса и на выходе из поворотного колена, что может способствовать дополнительной диссипации энергии.

Другой важный результат – обнаруженная сильная неравномерность потока за поворотным коленом. В результате того, что закрутка потока осуществляется по часовой стрелке, а у канала есть выделенное направление, интенсивный поток прижимается к левой стенке. У противоположной стенки, где направление закрутки противоположно направлению течения, поток тормозится, образуя обширную застойную область. Таким образом, проходное сечение в диффузоре отсасывающей трубы используется лишь менее чем на 1/3, что сильно снижает ее – 501 – пропускную способность. Этот эффект, очевидно, также будет приводить к дополнительным потерям энергии и требует специального внимания при разработке конструкций практических гидротурбин.

Полученные результаты совместного экспериментального и численного моделирования будут использоваться для оптимизации геометрии отсасывающей трубы для снижения потерь энергии потока и расширения диапазона устойчивой работы гидротурбин.

Работа выполнена при поддержке Министерства образования и науки Российской Федерации в рамках реализации Федеральной целевой программы «Научные и научнопедагогические кадры инновационной России» на 2009 – 2013 годы.