Численное исследование динамического поведения вращающихся конструкций
Автор: Шевелев Николай Алексеевич, Домбровский Игорь Викторович
Статья в выпуске: 1, 2009 года.
Бесплатный доступ
Предлагается алгоритм численного решения задачи о свободных и вынужденных колебаниях вращающихся динамически симметричных тел, основанный на методе конечных элементов. Кроме задачи о собственных частотах и формах колебаний вращающихся упругих тел для получения полной информации о «динамическом паспорте системы» необходимо рассмотреть задачу неконсервативной упругой устойчивости. В зависимости от характера найденных собственных значений можно сделать заключение об устойчивости, например, в рамках теорем Ляпунова об устойчивости по первому приближению или показать, что эти собственные значения соответствуют собственным частотам колебаний. Собственные формы неконсервативной задачи предлагается искать в виде разложения по собственным формам консервативной задачи, что снижает размерность матриц и позволяет решать комплексную проблему собственных значений с использованием уже разработанных и апробированных схем. Построены амплитудно-частотные характеристики неконсервативной системы для различных значений параметра угловой скорости. Значения последнего соответствуют устойчивому и неустойчивому режиму.
Амплитудно-частотные характеристики, колебания, конечные элементы, формы колебаний, устойчивость, вращающееся упругое тело, численная модель
Короткий адрес: https://sciup.org/146211310
IDR: 146211310 | УДК: 539.3:
Текст научной статьи Численное исследование динамического поведения вращающихся конструкций
Предлагается алгоритм численного решения задачи о свободных и вынужденных колебаниях вращающихся динамически симметричных тел, основанный на методе конечных элементов.
Кроме задачи о собственных частотах и формах колебаний вращающихся упругих тел для получения полной информации о «динамическом паспорте системы» необходимо рассмотреть задачу неконсервативной упругой устойчивости. В зависимости от характера найденных собственных значений можно сделать заключение об устойчивости, например, в рамках теорем Ляпунова об устойчивости по первому приближению или показать, что эти собственные значения соответствуют собственным частотам колебаний.
Собственные формы неконсервативной задачи предлагается искать в виде разложения по собственным формам консервативной задачи, что снижает размерность матриц и позволяет решать комплексную проблему собственных значений с использованием уже разработанных и апробированных схем.
Построены амплитудно-частотные характеристики неконсервативной системы для различных значений параметра угловой скорости. Значения последнего соответствуют устойчивому и неустойчивому режиму.
Постановка задачи о свободных колебаниях
В трехмерном евклидовом пространстве упругое тело занимает объем V , ограниченный поверхностью L . На части поверхности L u заданы граничные условия в перемещениях, на остальной части La - граничные условия в напряжениях. Вращение происходит с угловой скоростью to , постоянной по величине, вокруг оси, совпадающей с осью симметрии тела. Учитываются относительные, кориолисовы и центростремительные ускорения, связанные с упругими деформациями тела. Влияние стационарных внутренних усилий, вызванных действием центробежных сил, не рассматривается. Подлежат определению динамические характеристики системы, собственные значения и собственные формы движения, возникающие около стационарного положения. Другими словами, необходимо определить функциональную зависимость возмущений от времени.
Математическая постановка задачи включает в себя уравнения движения [1], [4]:
( X + ^ )grad ( div ( u ) ) + цА и = p [ u + 2щ х u + щ х (щ х u ) ] , (1)
где u – вектор перемещений во вращающейся цилиндрической системе координат r,z, фе V, ось z которой направлена по вектору щ; р - плотность материала тела; X , ц - параметры Ламе.
Работа выполнена при финансовой поддержке РФФИ проект № 09-08-99121-р_урал_офи.
Граничные условия в перемещениях на части поверхности L u и в напряжениях на части поверхности Lo (L = Lu + LO)
u ( r , z , ф , t ) = 0, r , z , фЁ L u , н -о ( u ) = 0 , r , z , фЁ Lo , (2)
где о - тензор напряжений в цилиндрической системе координат; н - вектор внешней нормали к поверхности L .
Компоненты тензоров напряжений и деформаций в случае изотропного линейного материала связаны физическими соотношениями:
о = 10 E + 2це .(3)
Здесь 0 - первый инвариант тензора деформаций, Е - единичный тензор второго ранга. Для компонент тензора деформаций и вектора смещений имеют место соотношения Коши:
е = 2 [(vu)T + Vu] .(4)
Искомый вектор перемещений для рассматриваемой задачи представляется в виде
u(r, z, Ф, t) = U(r, z, Ф)ep,(5)
где р – комплексное собственное значение, имеющее смысл собственной частоты колебаний или параметра устойчивости.
После подстановки выражения (5) в уравнения (1) и граничные условия (2) получим формулу для отыскания вектора U , который представляет собой форму колебаний, если р – мнимое число, или форму потери устойчивости, если действительная часть комплексного р или действительное р больше нуля, краевую задачу
( 1 + ^ )grad ( div ( u ) ) + ^A u = p [ p 2 U + 2 p щ х U + щ х (щ х U ) J , r , z , фЁ V ,
U ( r , z , ф ) = 0, U ( r , z , ф ) = 0, r , z , фЁ L u , (6)
н - { 10 E + Ц ( V U ) T + ( V U ) } = 0, r , z , фЁLо .
При использовании численных методов отыскания вектора перемещений удобней использовать вариационную формулировку:
8 A o + 8 A i + 8 A c + 8 Ak = 0, (7)
8 A o = - j о - 8e dV , 8 A i = -p p 2 j U - 8 U dV ,
8 A c = - j p [ щ х ( щ х U ) J 8 U dV , 8 A k = - 2 p p j ( щ х U ) 8 U dV .
Здесь 8 A c - работа внутренних напряжений, определяемая возможными перемещениями, 8 A i - работа сил инерции, 8 A c - работа центробежных сил, связанных с полем перемещений U , 8 A k - слагаемое, определенное силами Кориолиса. Интегрирование ведется по объему V .
Искомый вектор перемещений U и его вариация 8 U должны удовлетворять граничным условиям в перемещениях, а условия в напряжениях выполняются автоматически.
Численная реализация
Геометрическая симметрия рассматриваемых тел относительно оси вращения позволяет записать искомый вектор U ( r , z , ф ) в виде разложения по окружной координате ф :
u
Г NL
X
U = < w > = <
v
i =1
N X l =1
N
X
us s ( r , z ) cos( l ф ) + u la ( r , z ) sin( l ф )
w s ( r , z ) cos( l ф ) + w la ( r , z ) Sin( l ф ) > , v ( r , z ) cos( l ф ) + v la ( r , z ) sin( l ф )
1 1 =1
где u , w , v - компоненты вектора U по координатам r , z , ф соответственно, индекс s соответствует симметричным и а – антисимметричным составляющим вектора относительно радиуса ф = 0, суммирование ведется от l = 1 до l = N .
В символической форме вектор перемещений запишется в виде
U = U s + U a .
Если в вариационном уравнении не учитываются слагаемые 8 A c и 8 Ak , связанные с вращением ( w= 0), то задача определения U распадается на две самостоятельные для U s и U a , а соответствующие собственным векторам собственные значения p s и р а совпадают. В случае неконсервативной системы формы U s и U a связаны и определяются из общего уравнения (7), а вектор U – их суперпозиция. Для вариации 8 U примем разложение, аналогичное (8). Вычисление интегралов, входящих в (7), при учете представления U и 8 U в виде (8) и свойств ортогональности тригонометрических функций приводит к вариационной задаче для отдельной гармоники l в разложении (8).
На этапе численного построения векторов U s и U a применяется процедура метода конечных элементов.
Конечно-элементный аналог вариационного уравнения (7) запишем в виде
(K + рp 2M + р w 2Fc + 2wpp Fk )8 = 0,
K = JBTDBdV, M = J NTNdV , Fc = J NTfcdV , F, = J NTfkdV, где K,M,Fc,Fk – матрицы жесткости, масс, центробежных сил и сил Кориолиса. Матрица fc определяется через функции формы элемента и является симметричной, а матрица fk – антисимметричной. Если сделать замену переменной:
4 = t Q-1, Q ,(11)
d t02
и положить Q = to , то можно уравнение (10) переписать в виде
(K0 + poM0 + p 0F )8 = 0,(12)
где матрицы с нулевым индексом отличаются от соответствующих матриц из (10) множителями, a p = p 0 Q . Такая замена переменной t и выбор Q приводит к нормировке численного значения элементов матриц K , M , F c , F k и их равноценному вкладу в результирующие коэффициенты системы (12). Комплексные собственные значения p 0 , входящие в систему линейных алгебраических уравнений как неизвестные параметры, определяем методом парабол в комплексной форме. Такую схему решения поставленной задачи будем называть прямым методом отыскания собственных значений. К ее недостаткам надо отнести высокий порядок системы уравнений (12) и низкую эффективность метода парабол в комплексной форме для матриц высокой размерности.
Для снижения размерности системы воспользуемся методом разложения по собственным формам соответствующей задачи для консервативной системы. Последняя задача, будучи действительной, существенно проще комплексной задачи (12).
Разложение включает линейные комбинации конечного числа первых собственных форм колебаний соответствующей упругой задачи без учета вращения [3]:
m
8 = Е q , ч к , (13)
к =1
( ч k – собственные формы колебаний). Для их определения решается алгебраическая задача
( K -рЛ 2 M ) ч к = 0, (14)
где Л к - собственная частота колебаний консервативной системы, ч к - собственная форма колебаний, соответствующая Л к . При учете (13) система (12) преобразуется в систему
( K + p 2 m '+ p „ f ; ) q = 0. (15)
Матрицы в (15) имеют размер 2т х 2т , их элементы определяются соотношениями:
K j = ч K 0 ч у , M l3 = ч Т M 0 ч у , F ^ ) у .= ч F ; 0 ч у , г , j = 1,2,... m (16)
Размер матриц в два раза больше числа удержанных членов разложения, что связано с необходимостью учета симметричных и антисимметричных компонент в векторах ч k .
Метод разложения по собственным формам удобно использовать при варьировании свойств материала конструкции и параметра угловой скорости, когда полученные заранее формы колебаний многократно могут быть использованы при исследовании устойчивости. Однако трудно определить заранее необходимое число собственных форм в разложении (13).
Проведенные расчеты показывают, что этот недостаток компенсируется существенным повышением эффективности метода отыскания собственных значений, а проведение численного эксперимента с различным количеством удержанных в разложении форм гарантирует правильность полученных результатов.
Примеры расчета
Численные расчеты были выполнены для упругого тела, имеющего форму диска следующих геометрических размеров: внутренний радиус 0,02 м, наружный – 0,125 м, толщина 0,01 м, жестко закрепленного по внутреннему контуру, коэффициента Пуассона 0,26. По внешнему контуру диск свободен от нагрузок. Для оценки работоспособности предлагаемых алгоритмов задача решалась прямым методом и методом разложения по собственным формам консервативной системы. Кроме того, результаты, полученные при построении собственных форм колебаний консервативной задачи, дают возможность определить необходимое количество членов в разложении (13).
Все результаты, приведенные в работе, относятся к первой гармонике в разложении по угловой координате. Первым пяти собственным частотам соответствуют изгибные формы колебаний, шестая частота имеет форму колебаний в плоскости r , ф , седьмая вновь изгибная и т.д. (чередование изгибных и плоских форм колебаний). Для различных геометрических размеров дисков и граничных условий порядок их следования может изменяться.
На рисунке приведены графики изменения первого и шестого собственных значений в зависимости от параметра угловой скорости. Сплошными линиями дано изменение мнимой части комплексного собственного значения, штрихами – действительная часть соответственно.
Влияние дополнительных сил инерции, вызванных вращением, по-разному сказывается на изменении собственных значений как в количественном отношении, так и качественно. Те собственные значения, которым соответствуют изгибные формы колебаний, с увеличением угловой скорости могут убывать, оставаясь чисто мнимыми (см. рисунок), p1 , до тех пор, пока хотя бы одно из них не обратится в нуль. При дальнейшем увеличении ω величина p1 , например, становится действительной и положительной, причем изменение таких собственных значений происходит довольно медленно. Согласно известным исследованиям [2], [3] такой тип неустойчивости называется статической неустойчивостью. Шестое собственное значение, соответственно плоская форма колебаний, на изменение угловой скорости реагирует совершенно иначе, чем упомянутые выше изгибные частоты.
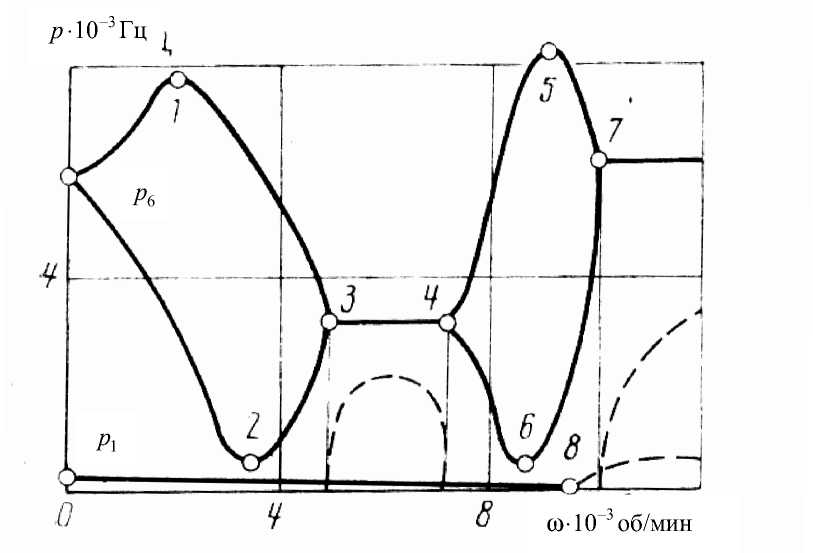
Рис. Изменение собственных значений в зависимости от параметра угловой скорости
Напомним, что в случае ω = 0 имеем кратные собственные частоты, соответствующие симметричным и антисимметричным формам движений. При появлении угловой скорости они начинают изменяться количественно, оставаясь чисто мнимыми (см. рисунок), по весьма сложному закону. Начиная с некоторого значения параметра ω они сближаются, образуя пару комплексных собственных значений с положительной действительной частью. Такой эффект описан [2] как колебательная неустойчивость.
При получении этих результатов был использован прямой метод и метод разложения по собственным формам. Сравнение показало практическое совпадение собственных значений, полученных обоими методами, при удержании в разложении 16 собственных форм колебаний.
Вынужденные колебания с учетом вращения и диссипации
Остановимся на определении динамической реакции системы на внешнее кинематическое возбуждение. Решение построим прямым методом. Основная цель этого исследования заключается в построении амплитудно-частотных характеристик неконсервативной системы для различных значений параметра угловой скорости ω . Значения последнего должны соответствовать устойчивому и неустойчивому режиму.
Кроме того, полученные здесь результаты будут являться дополнительной проверкой правильности решения задачи о свободном движении для неконсервативной системы.
Решение поставленной задачи о вынужденных колебаниях вращающегося осесимметричного тела будем искать в виде
U ( r , z , ф , t ) = ( U 0 + U - ) cos ( Q k t ) + ( U 0 + U 5 ) sin ( Q k t ) , (17)
где U 0 ( r , z , ф ) и U 0 ( r , z , ф ) - амплитуды заданного кинематического возмущения; Q k - частота кинематического возмущения.
Согласно полуаналитическому методу конечных элементов раскладываем искомые перемещения в ряд по угловой координате:
(U + U0
и =) V + V
W + W0
тс
У [( U -- + U 0 c ) cos( l ф ) + (U -- + U 0е ) sin( l Ф )] cos( Q k t ) l =1
тс
У [( V " + v ;- ) cos( l ф ) + ( V -c + V ac )sin( l ф )] cos( Q k t ) l =1
тс
+
У [( W -- + W0 ce ) sin( l ф ) + ( W -- + W 0 -c ) cos( l ф )]cos( Q k t )
. l =1
У [( U -5 + U 0 ’ )cos( l ф ) + (U - + U - )sin( l ф )]sin( й k t )
l =1
тс
+ У [(Vе5 + V) cos( l ф) + (V- + V-) sin( l ф)] sin(Q kt) [ l=1
тс
У [( W -5 + W 0 -5 ) sin( l ф ) + ( W -5 + W 0 -5 ) cos( l ф )] sin( Q kt )
l =1
где U 0, W 0, V0 - компоненты заданного кинематического возмущения.
Будем разыскивать неизвестные симметричные U--, W--, Vе-, U-5, W-5, Vе5 и антисимметричные U--, W--, V--, U-5, W-5, V-5 перемещения методом конечных элементов. Используя конечно-элементную модель, запишем для произвольного элемента соотношения (18) в виде тс и = У Nl (дl)'" cos(nkt) + Nl (дl)“” sin(Qkt), (19)
l =1
где (дl )cos = (дl)- + (д0)-, (дl )sin = (дl)5 + (д10)5; (дl)-, (дl)5 - неизвестные узловые перемещения;
( д. 1 ) - . ( д 0 ) 5
- заданные узловые перемещения.
В отличие от упругого тела в этом случае матица D имеет вид
D = D * - G *+ D 0 ■ K .
С учетом равенства (20) вариационное уравнение в конечно-элементной форме примет для произвольного элемента вид
|
K * G |
( cos( Q k t ) — j R ( t — т )cos( Q k т ) d т ( д i ) + K G ( sin( Q k t ) — ( —^ J |
t
j R ( t - т ) sin( Q k т ) d т ( д i ! + K ■ K 0 cos( Q kt ) ( д i ) cos + K ■ K 0 sin( Q kt ) ( д i ) sm
-
—^
—QkpMcos(Qkt)(дi )cos — QkpMsin(Qkt)(дi ! mpF cos(Qkt)(Дi Г — w'pF sm(Qkt) (дi )sin — 2wQkpFk sm(Qkt) (дi )sin +
+ 2 ®Q k P F k cos( Q k t ) ( д i ) cos = K * G ( cos( Q kt )(1 — Г с ) — Г s sin( Q kt ) )( д i Г + + K * G ( sin( Q k t )(1 — Г с ) — Г s cos( Q k t ) )( д i Г +
+ K ■ K 0 cos( Q kt ) ( д i ) cos + K ■ K 0 sin( Q kt ) ( д i Г — Q k p M cos( Q kt ) ( д i Г —
—Q k p M sin( Q k t ) ( д i ) sin — ® 2 p F cos( Q k t ) ( д i ) cos — ® 2 p F sin( Q k t ) ( д i ) sin —
—2®QkpFk sin(Qkt) (дi )sin + 2®QkpFk cos(Qkt) (дi Г = 0, где
R ( t — т ) = A
e -e( t —т )
(t — т)1—a
7e—pe
Гс = A [e r- cos Q,9 d 9 , с J fil—a k
0 9
7e—pe
Г = A\— - sin Q,9 d 9 , s j g1 — « k ,
k* = j (в e) T d*b edve,
Ve
K = j ( B e ) T D 0 B e dV e .
Ve
Система уравнений (21) распадается на две подсистемы:
( G ■ K * (1 — Г с ) + K ■ K 0 — Q k p M ^ ' P F ) ( д i ) cos +
+ ( G ■ K * (1 — Г с ) + 2 ®pQ k F k ) ( д i ) sin = 0,
(G ■ K*(1 — Гс) + K ■ K0 — QkpM — ®2pFc) (д i )sin —
-
— ( G ■ K * (1 — Г с ) + 2 ®pQ k F k ) ( д i ) cos = 0,
из которых можно найти неизвестные узловые перемещения при заданных значениях Ω k и ω .
Предложенный алгоритм исследования установившихся вынужденных колебаний реализован для случая кинематического возбуждения. Получены качественно новые результаты, относящиеся к динамической реакции неконсервативной системы на гармоническое возбуждение. Особенности динамической реакции неконсервативной системы (с учетом вращения) на внешнее кинематическое возбуждение заключается в появлении широких зон повышенной амплитуды, а не отдельных резонансных пиков, как это было в случае консервативной системы. Ширина этих участков зависит от величины угловой скорости.


