Численное исследование динамики кельтского камня на плоскости с вязким трением

Кельтский камень - это выпуклое твердое тело, одна из главных центральных осей которого перпендикулярна, к поверхности тела, а. направления главных кривизн поверхности в точке пересечения с этой осью не параллельны двум другим главным осям. Хорошо известно, что устойчивость вращений такого тела, вокруг вертикальной оси может зависеть от направления вращения. В большинстве работ, посвященных этому свойству, рассматривается неголономная постановка, задачи, т.е. считается, что скорость точки контакта, тела, с плоскостью равна, нулю (см., например, [1], [2]). Однако, например, в работе [3] указывается на. недостаток такой постановки, т.к. она. не подтверждается физическими соображениями. В той же работе рассматривается движение кельтского камня на. плоскости с поликомпо-нентным трением и подтверждается согласованность такой постановки задачи с натурными экспериментами.

В настоящей работе продолжается исследование [1], в котором предполагается, что со стороны плоскости на камень действует сила вязкого трения. Эта модель трения позволяет провести не только численные, но и аналитические исследования в рассмариваемой задаче. Кроме того, при стремлении коэффициента, вязкого трения к бесконечности сила, вязкого трения реализует неголономную связь [4].

• 2.    Постановка задачи

Пусть v - скорость центра масс выпуклого тела, уравнение поверхности которого имеет вид /(г) = 0, ш его скорость тела, ад- единичный вектор восходящей вертикали. Тогда радиус-вектор точки контакта тела с плоскостью определяется равенством д = —grad f(г)/| grad f(г)|, а скорость этой точки имеет вид u = v + [ш, г].

На тело действуют сила тяжести —тдд, нормальная компонента реакции опорной плоскости N = Nд и сила вязкого трения F = — mku. Уравнения движения тела, записанные в его главных центральных осях, имеют вид mv + [w,mv] = (N — тд)д + F,(1)

7ш ■ ш, Jш] = [г, Nд + F],(2)

д + [ш, д ]=0,(3)

(v + [ш, г], д) = 0.(4)

Здесь J = diag(A1, A2, A3) - главный центральный тензор инерции тела. Уравнение (1) выражает теорему о движении центра масс тела, (2) - теорему об изменении кинетического момента относительно центра масс, (3) - условие постоянства вектора восходящей вертикали, а (4) - условие контакта тела с плоскостью. Найдем из полученной системы нормальную реакцию опорной плоскости

N = т (д + ([г, ш] + [Г, ш], д)) + ([ш,т], [ш, д]))                       (5)

и далее будем рассматривать систему (1)-(3), учитывая (5). Заметим, что если в течении движения величина N обратится в ноль, то произойдет отрыв тела от опорной плоскости. В этом случае в качестве уравнений движения следует рассматривать (1)-(3), положив в них N = 0 и F = 0 и добавив к ним уравнение 2 = (v + [ш, г], д) (в момент отрыва и при возвращении на контакт 2 = 0).

Рассматриваемая система уравнений имеет решения вида щ = ^2 = V3 = 0,  Д1 = Д2 = 0,  Дз = 1,  Ш1 = Ш2 = 0, Шз = ш (ш Е R).(6)

Им соответствуют равномерные вращения тела вокруг перпендикулярной его поверхности главной оси инерции, совпадающей с вертикалью. Уравнение поверхности тела при дз = 1 можно представить в виде

.               (жі cos 5+ж2 sin 5)2    (жі sin 5—ж2 cos 5)2,

J (г) = жз + аз — ---------------- — --------------- + Оз(жх,Ж2),

2а12а где аі, а2 - главные радиусы кривизны поверхности тела в точке контакта, аз -высота центра масс, 5 — угол между векторами главных кривизн и главными осями. Рассматриваемое тело является кельтским камнем, если выполнены соотношения А1 = А2, а1 = а2, 5 = 0 (mod тг/2).

• 3.    Условия устойчивости

Линеаризованные уравнения возмущенного движения системы в окрестности решений Eq. (6) и соответствующее характеристическое уравнение находятся в [1]. В случае неголо-номной постановки задачи (k ^ +то) условия устойчивости имеют вид [1], [2]:

Аі < А2 < Аз, аі > а2 > аз, 0 < 5 < ^,(7)

J = (Аі+А2 — Аз) (- + - — 2^ — таз f4—3 (- + -) +2--) > 0,(8)

\аз аз /        У     у аз аз/ аз аз/

22 тд z ш < 0, ш > ш* = ——(а1 — аз)(а2 — аз).(9)

Jаз

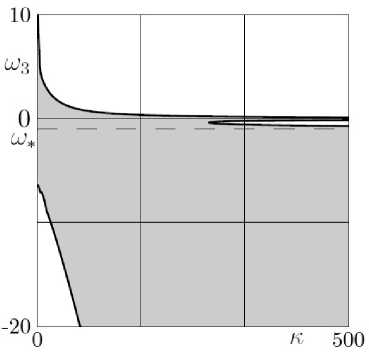
Рис. 1. А 1 = 3, А 2 = 4, A 3 = 5, а 1 = 5, а₂ = 4, йз = 3 т = 1, 5 = 0.75; J = 7, ш* = -0.97

Условие (7) означает, что вращение происходит вокруг оси наибольшего момента инерции, и соответствующее равновесие (ш = 0) устойчиво. Условие (8) накладывает ограничения на геометрические и динамические параметры тела. Неравенство (9) означает, что устойчивы только вращения в отрицательном направлении и с достаточно большой угловой скоростью.

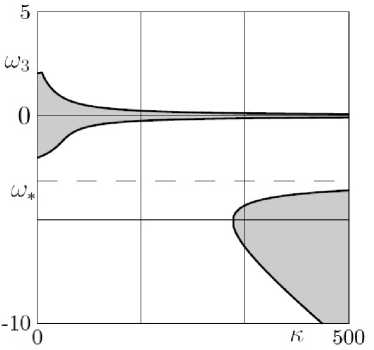
Рис. 2. А 1 = 3, А 2 = 4, Аз = 5, а 1 =5, а ₂ =4, йз =2, т = 1, 5 = 0.75; J = 3, ш* = -3.13

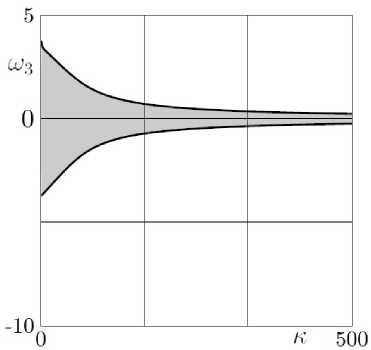
Рис. 3. А 1 = 3, А 2 = 4, Аз = 5, а 1 = 5, а ₂ = 4, йз =2, т = 3, 5 = 0.75,   J = —1 < 0

В случае произвольного коэффициента вязкого трения линеаризованные уравнения возмущенного движения системы в окрестности решений (6) довольно громоздки [1] и аналитический анализ условий устойчивости затруднителен. Но при заданных параметрах задачи области устойчивости могут быть построены численно (рис. 1, рис. 2, рис. 3). В случае, приведенном на рис. 1, при достаточно больших коэффициентах трения кроме соответствующей неголономной постановки задачи области (ниже пунктирной прямой) существует еще узкая область в окрестности нуля. При уменьшении к эти области сливаются в одну, содержащую в себе почти все отрицательные значения ш и малую область положительных значений ш. А при совсем малых к область устойчивости приобретает некоторую симметрию относительно горизонтали.

В случае, приведенном на рис. 2 (который отличается от предыдущего только высотой центра масс), область устойчивости разделяется на две части: соответствующую неголо-номному случаю область и область в окрестности равновесия. А в случае, приведенном на рис. 3 (увеличивается масса тела), остается только область устойчивости в окрестности равновесия.

Реальной модели кельтского камня, демонстрирующей в натурных экспериментах зависимость устойчивости вращений от их направления, соответствуют параметры

А1 = 0.058 • 10-3, А2 = 0.44 • 10-3, A3 = 0.49 • 10-3, оі = 0.661, 02 = 0.073, оз = 0.0098, т = 0.1, 5 = 0.1, J = -0.007 < 0.

Область устойчивости перманентных вращений для указанной модели представлена на рис. 4. Соответствующей неголономной постановки задачи области устойчивости в этом случае не существует, и при любом коэффициенте трения существуют устойчивые вращения как в положительном, так и в отрицательном направлениях.

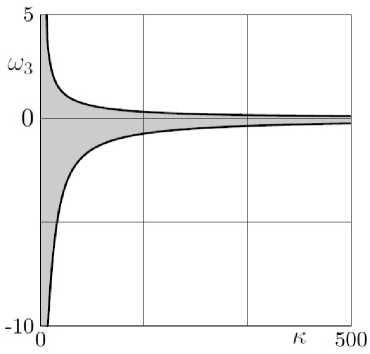
Рис. 4

4.    Численные эксперименты

Численные эксперименты проводились на плоскости с коэффициентом трения к = 30 с 1. Начальные условия имели вид

7 2 (0) = 0,   ш і (0) = Ш 2 (0) = 0, u(0) = 0.

На рис. 5 слева представлены результаты экспериментов с различными начальными угловыми скоростями вращений при очень малом начальном отклонении от вертикали (7з(0) = 0.9999). по центру - при чуть> большем отклонении (73(0) = 0.999). а справа, -при еще большем (73(0) = 0.99). Серым цветом выделена область устойчивости вращений при выбранном коэффициенте вязкого трения. Как мы видим, большинство устойчивых вращений имеют очень малую область притяжения. В частности, при положительных начальных угловых скоростях вращения имеет место смена направления вращения с последующим выходом на устойчивые равномерные вращения в отрицательном направлении.

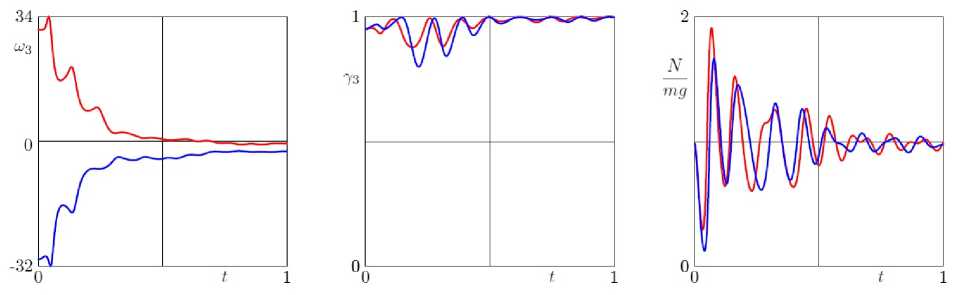
Рис. 5

Заметим, что в представленных на рис. 5 случаях отклонения главной оси тела от вертикали достаточно малы, а величина нормальной реакции опорной плоскости почти равна весу тела. При больших угловых скоростях вращения (рис. 6) наблюдается такое свойство камня, как переход вращательных движений в колебательные и обратно. При этом величина нормальной реакции опорной плоскости меняется существенно, что означает возможность отрыва тела от плоскости.

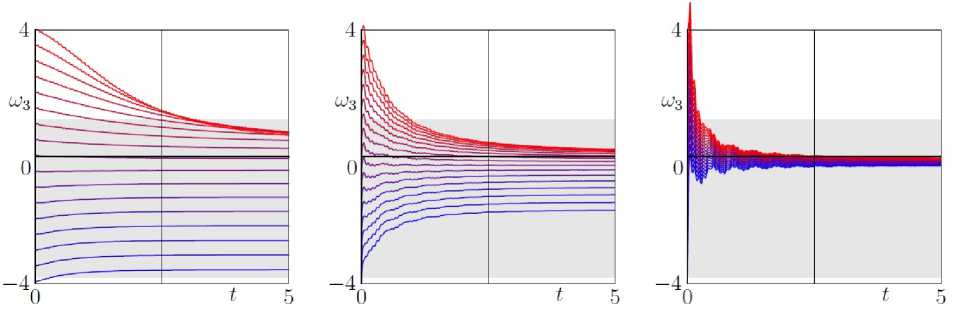
Рис. 6

5.    Заключение

Таким образом, результаты моделирования взаимодействия кельтского камня с опорной плоскостью силой вязкого трения согласуются с известными свойствами его динамики и имеет смысл дальнейшее исследование рассмотренной задачи. Кроме того, достаточная простота выбранной модели полагает возможным аналитическое исследование этих свойств.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (19-01-00140, 18-01-00335) и Программы фундаментальных научных исследований по приоритетным направлениям, определяемым Президиумом Российской академии наук, № 7 «Новые разработки в перспективных направлениях энергетики, механики и робототехни ки».