Численное исследование характеристик тепловых труб в составе радиоэлектронного оборудования космических аппаратов
Автор: Кулагин В.А., Соколов Н.Ю.
Журнал: Журнал Сибирского федерального университета. Серия: Техника и технологии @technologies-sfu
Статья в выпуске: 6 т.8, 2015 года.
Бесплатный доступ
Т-образная плоская тепловая труба (ТТ) предназначена для использования в конструкциях космических аппаратов (КА). В статье изложена разработанная математическая модель для расчета теплового режима работы изделий с использованием плоских тепловых труб, основанная на решении двумерных стационарных уравнений сохранения массы, дополненных уравнениями Дарси для жидкости и пара. Для заданного расположения источников и стоков тепла на поверхности плоской тепловой трубы рассчитаны распределения давлений и потоков массы для обеих фаз теплоносителя. Анализ работоспособности тепловой трубы для заданных условий основан на проверке выполнения капиллярного ограничения.
Плоская тепловая труба, космические аппараты, математическая модель, теплоноситель
Короткий адрес: https://sciup.org/146115004
IDR: 146115004 | DOI: 10.17516/1999-494X-2015-8-6-769-773
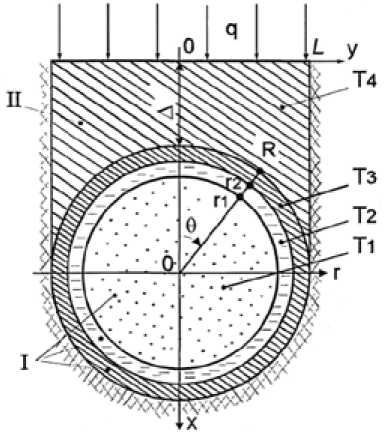
Список литературы Численное исследование характеристик тепловых труб в составе радиоэлектронного оборудования космических аппаратов
- Деревянко В.А., Нестеров Д.А., Косенко В.Е. и др.//Вестник СибГАУ. 2013. № 6(52). С. 111-116.
- Колоусова А.А. Математическоемоделированиетеплопереносавсистеме«источниктепловыделения -соединительный элемент -тепловаятруба». Томск, 2004.
- Рид Р., Праусниц Дж., Шервуд Т. Свойствагазови жидкостей. Л.: Химия, 1982.
- Пасконов В.М., Полежаев В.И., Чудов Л.А. Численное моделирование процессов тепло-и массопереноса. М.: Наука, 1984. 288 с.
