Геофильтрационная задача о движении углеводородного загрязнителя и воздуха с учетом гравитационного влияния в трехмерной постановке описывается системой уравнений:

m9s_+ 8(риД ! 5(риД ! 5(риД = 8t дх ду 8z m8fL-sf+ 5(риД ! 9(puf) S(pMj

8t Эх 8y 8z

_M ^AM(v_A-_P1g ),     (2, a)

lf = -k^^-(Vp₂-p₂g ).        (2,6)

ti-2

Начальные условия:

• -при/=0: s_x=s₂ ,s = sfx,y),p = p₀ наГ_р

s = 0,p=p наГ..              (3)

• - начальное давление p_x = p, g H распределено no

  законам гидростатики. Изменением давления р₂ можно пренебречь и принять его величину близкой к атмосферному давлению, так как плотность загрязнителя р, значительно больше плотности воздуха р₂.

  Граничные условия:

  - на верхней границе рассматриваемой области граничное условие для s(x, у, z, t) и р(х, у, z, f) при t е (0; 7] имеет вид

  s = »₀(х, у, I), р = р₀ (х, у, f) на Г_р (4)

  
  

  ницаемость к^ обращается в нуль. Учитывая (7) и (8), получим

  
  

  8s к^/     -

  _т =div к --- V_A-_P1g St           Pj ^v

  
  

  (И)

  
  

  Р=Р

  
  
  
  

  ^-0.

  8п

  
  
  
  

  Основным способом решения таких задач являются численные методы [1-6]. Среди них чаще всего применяют разностные методы благодаря их универсальности и наличию хорошо разработанной теории. В результате дискретизации дифференциальных уравнений с помощью метода конечных разностей непрерывное распре

  
  

  где и - вектор нормали к границе Г₂.

  На нижней границе рассматриваемой области граничное условие для s(x,y, z, t) и р(х,у, z,f)t е (0; 7] имеет вид

  
  

  ^^М₍у_А -_Plg )=о

  
  
  

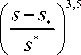
  S,

  
  
  
  

  0,    0 < s < s,,

  
  

  ^₂С0 = <

  
  
  

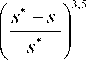
  (1 + 35), 0< S< S*,

  0,

  
  

  деление параметров заменяется дискретным.

  Метод конечных разностей включает следующие основные этапы:

  • -    построение сетки, охватывающей рассматриваемую область;

  • -    построение на полученной сетке конечно-разностной аппроксимации, эквивалентной исходному дифференциальному уравнению и дополнительным условиям;

  - формирование на основе конечно-разностной аппроксимации системы алгебраических уравнений и ее решение.

  Чтобы построить разностную схему для исходной задачи, выберем равномерную сетку с шагом h по переменной z, с шагом h_x по переменной х, с шагом h по переменной у и шагом т по времени t. Получим сеточную область:

  
  

  5* < 5 < 1.

  
  

  w, = (z = i.h (0 < z. <  п ), х_ =

  ^v zl 1 z ^v          1       z⁷’ z2

  
  

  Математическая модель (1)...(8), основанная на двухфазной фильтрации в физических переменных с учетом

  
  

  ^{= i}K^ - 4 ^п)Д_в⁼

  
  

  гравитационного влияния, позволяет определить:

  - распределение скоростей фильтрации в грунте в любой момент времени;

  - распределение давления в каждой из фаз р_р

  
  

  - насыщенность s

  Подставим уравнения (2) в уравнения неразрывности

  
  

  (1). В результате получим:

  
  

  8s 8 ,k.(s)( др.

  т— = —к —- —^L

  8t 8z Ц; ( 8z

  
  

  Pig +

  
  

  ^{= 1}ДД < i₃< n), t=i№

  где и = LJh,n = LJh,n = LJh ,n=T!i. z 1 z’ x 2 x' у 3 у’ t

  Заменим производные во внутренних узлах w_{h т} конечно-разностными отношениями с учетом представления переменного коэффициента и получим явную разностную схему [7]:

  
  

  ⁹pA ^{9 5a}

  8x Pj Эх) 8y Pj 8y

  
  
  
  
  

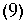
  S(l-s) 8 (^k₂(s) dp₂

  8t           p₂ 8z

  
  

  hz

  
  
  
  
  
  
  
  
  

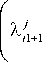
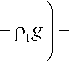
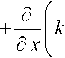
  k^ 8p₂ p₂ 8x

  
  

  8 Ck₂(s)dp₂

  14 ⁹y

  
  

  P_c^=p₂-p_v

  Уравнения (9) после преобразований примут вид (в безразмерной форме)

  
  

  div

  
  

  I 14     14

  
  

  Vfl-p^-- )                  14 .

  
  
  
  

  + div

  
  

  к---- (л(⁵)-Р2§)

  14 ^х             ’

  
  

  Рассмотрим важное обстоятельство, когда предельное значение насыщенности s* = 1, при котором фазовая про

  
  
  
  
  
  
  
  
  
  
  

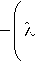
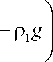
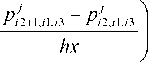
  '12+1/2,11,13

  
  
  
  
  
  

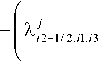
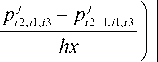
  Л j Рв+1,п,п Pii,il,i2 Л'/З+Г 2,11,12            ;

  hy

  
  
  
  
  

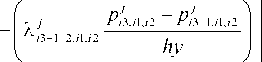
Xx^ = k^l, Хфх^кЬР!,

Hi ' Н2

⁸м ,■ = °- j = °- Ч ^{= 0}» -ML ~Ь

1₂ =о......,»,-!; /3 =0, ...л_¥ -1;

4_А =L Ч =°- ⁰⁵&Д =3;

% =°- Ч =°- 33 <и„-1;

Роу, =№ Ч =°; 0₂,/₃ =3;

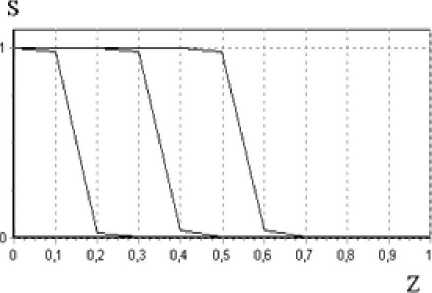
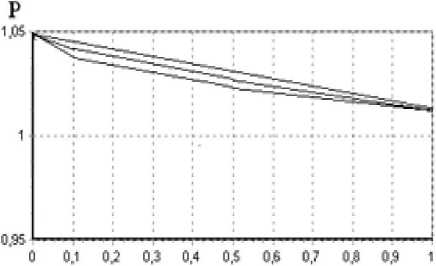
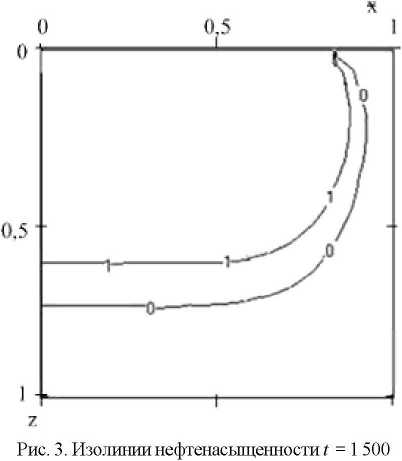
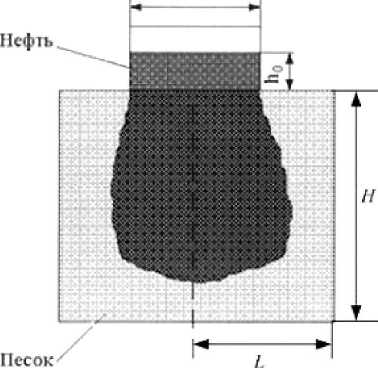
PJQiA =Р^ Ч =°; 3

=        Dj -0 2

1 ^n-uiPn j \..„Л, V где Х^ц(») =HSi +$^j)/2 .Разностнаясхема(12)алпрок-симирует исходное уравнение с погрешностью О(т + /г).

Систему уравнений (12) решаем итерационным методом. Формула позволяет получить решение s пр в явном виде. При этом на каждом временном слое вначале находим давление, а далее решаем параболическое уравнение для нефтенасыщенности. Эго приводит к необходимости подбора временного шага для устойчивости счета и сходимости итерационных процессов. В численных расчетах использовались шаги сетки /z 0.1. т 0.002.

В результате численного эксперимента, связанного с исследованием распространения нефтезагрязнителя в грунт под действием силы тяжести с учетом влияния давления. были проведены многовариантные расчеты. Значения фильтрационных параметров модели были приближены к экспериментальным данным и варьировались в следующих пределах:

• -    пористость грунта т = 0.05...0.4;

• -    проницаемость к= 1.15 10~³... 11,5 мкм²;

• -    плотность загрязнителя с = 1.1... 1.4 г/см³;

• -    вязкость загрязнителя м = 0.54...0.9 сПз;

• -    высота области фильтрации загрязнителя L = 1 м;

• -    предельные значения насыщенности / = 0.9; s, = 0.1; - насыщенность на верхней границе области ^ = 1.0; -ускорение свободного падения g = 9.8 м/с².

Разработанная математическая модель фильтрации нефтезагрязнителя учитывает движение несмачивающей жидкости и воздуха в пористой структуре.

Для проведения численных расчетов была реализована программа с использованием технологии визуального программирования Borland Delphi [8].

Поток по вертикали может служить хорошей аппроксимацией режима полного проникновения нефти, т. е. одного из трех качественно возможных режима ее просачивания [10]. Это дает оценку сверху для глубины проникновения углеводородов в грунт. В качестве примера на рис. 1 приведены распределения нефтенасыщенности по глубине в различные моменты времени, где фронт продвигается в виде прямой линии, расположенной по диагонали относительно координатной системы. Эго говорит об увеличении фронтовой насыщенности. Как показывают численные расчеты распространения загрязнителя под воздействием силы тяжести, сначала формируется фронт загрязнения, который далее двигается вглубь пористого грунта. Процесс протекает достаточно мед ленно (в данном случае скорость продвижения фронта приблизительно равна 4 • 10"4 в безразмерных единицах), что согласуется с экспериментальными данными [9; 10]. Форму фронта определяют кривые k(s). для этого варианта расчета в качестве модельных фазовых проницае-мостей были взяты функциональные зависимости (7) и (8). а также члены дисперсионного типа. Фазовые проницаемости являются экспериментально измеряемыми функциями насыщенности. Расчеты показывают, что вблизи источника нефтезагрязнения образуется зона загрязнения. далее фронт нефтенасыщенности образуется и продвигается в основном за счет действия гравитационных сил (рис. 2).

Рис. 1. Динамика распространения фронта при различных значениях безразмерного времени Г: 408; 857; 1 308

Рис. 2. Распределение давления при различных значениях безразмерного времени Г. 408; 857; 1 308

Z

Рис. 3. показывает пример результатов расчета для случая определения зоны загрязнения, выполненных для одного варианта параметров. Достоверность полученных результатов подтверждается удовлетворительным совпадением теоретических и экспериментальных данных.

Полезные качественные сведения о закономерностях движения углеводородов в пористой среде могут быть получены путем анализа природных условий и постановки экспериментов. Проведенные лабораторные исследования пропитки воздушно-сухого песка (TF= 10... 12 %) при комнатной температуре различными объемами нефти (Г = 150 мл и Й,= 100 мл) показали, что процесс протекания нефти происходит преимущественно в вертикальном направлении, но наблюдается также некото- рое растекание в боковые стороны. Эти данные совпадают с экспериментальными результатами, описанными в [9].

Было установлено, что вся нефть протекла в хорошо проницаемый песок со скоростью, приблизительно равной 3.7 • 10 'м/ч. Это объясняется тем, что гравитационный напор оказывается сильнее капиллярного противодействия в течение всего времени наблюдения. Чем меньше высота нефтяного слоя, тем слабее его растекание в стороны, поэтому боковые потоки ослабевают книзу (рис. 4).

У

Рис. 4. Динамика проникновения нефти при начальной высоте нефтяного слоя //  10 мм: Н - высота области фильтрации; L - полуширина области фильтрации;

D = 113 мм - ширина углеводородного пятна на поверхности; Г= 100 мл - объем нефти

Проведенные исследования показали, что построенная математическая модель позволяет прогнозировать формирование фронта загрязнения и давать оценку величины загрязненной зоны: глубины и ширины проникновения нефти в почву с заданными свойствами за данный промежуток времени, скорости движения углеводородного загрязнителя в почве, коэффициента фильтрации определяемого по ее скорости.

Разработанные алгоритмы и программы моделирования процесса оформлены в виде информационно-вычислительной системы, позволяющей численно анализировать влияние различных физико-механических параметров на характеристики процесса фильтрации.

Растущая опасность загрязнения почвы в результате аварийных разливов нефти и нефтепродуктов ставит проблему охраны окружающей среды. Решение этой проблемы осложняется тем, что для оценки загрязнения почвы еще не существует достаточно простых моделей, широко применяемых для практических расчетов. Вместе с тем исследования класса геофильтрационных задач ведутся давно и продолжаются до сих пор. Однако предлагаемые модели имеют слишком общий характер, в них не проводится разделение факторов на существенные и несущественные. Для решения рассматриваемой проблемы необходимо совершенствовать методы прогнозирования распространения загрязняющих веществ, с учетом физико-механических механизмов взаимодействия загрязнителей между собой и с пористой средой. Особенностью разработанной автором математической модели является то, что она имеет объектно-ориентированный характер.

Построенная модель и проведенные с ее помощью исследования распространения загрязнителей могут быть использованы для практических оценок экологической опасности различных хозяйственных объектов и при планировании природоохранных мероприятий.