Численное исследование методов поиска многомерных солитонов

В последние годы в связи с развитием оптических вычислительных систем стало активно развиваться математическое моделирование распространения лазерных фемтосекундных импульсов в нелинейных средах. Математическая постановка соответствующих моделей сводится к определению управляющих параметров, для которых нелинейная система уравнений в частных производных, кроме обычных решений, допускает существование решений солитонного вида [1–3].

Под солитонным решением [4] в работе подразумевается решение, локализованное в ограниченной области, быстро стремящееся к нулю вне этой области, сохраняющее свою конфигурацию со временем и имеющее один или несколько инвариантов.

Среди предложенных методов нахождения солитонов наибольшее распространение получили метод обратной задачи, спектральные методы и др. При этом лазерное излучение позволяет реализовать так называемые цветные солитоны, когда на нескольких частотах одновременно существуют и распространяются вместе оптические волны вдоль нелинейной среды. Эволюция этих солитонов описывается системами связанных уравнений Шредингера. Интерес к этим солитонам в литературе постоянно сохраняется в связи с многочисленными потенциальными приложениями их в задачах передачи информации оптическими методами. Экспериментальные исследования [1–3], выполненные в различных лабораториях, показали практическую реализацию солитонов данного типа.

Ниже предлагаются два итерационных метода M1 и M2 для поиска солитонных решений, подробно описанные в [5] и [6] соответственно, которые хорошо себя зарекомендовали при нахождении солитонных решений одномерных уравнений таких, как уравнение Кортевега-де Фриза, уравнение Sin-Гордона и нелинейного уравнения Шредингера. В настоящей работе методы M1 и M2 применяются к системе нелинейных уравнений Шредингера, описанной в [7], и приводится сравнение результатов, полученных с помощью предложенных методов, с результатами, полученными в работе [7].

Математическая постановка задачи. Распространение оптического излучения в среде с кубичной нелинейностью в аксиально-симметричном случае описывается следующей системой нелинейных уравнений Шредингера [7]:

• — + iD A r A + iD 1 ^d-A + i у A * Be - ^ikz +

a z                a t ²

+ i a A (| A |² + 2| B | ²) = 0,

B + iD a B + D  B + i Y a 2 e k +      (1)

d z     2 r ² д t ^{2    r}

+ 2 i a B (21 A |² + 1 B |²) = 0, 0 <  r <  R , 0 <  t <  T ,

0 < z < Z, k = k 2 - 2 k1, где A(z, r, t), B(z, r, t) – комплексные амплитуды гармоник; z – нормированная на длину пучка основной волны продольная координата; r – безразмерная координата; t – безразмерное время в сопровождающей импульс основной волны системе координат;

.   1 d r d) _ _                  .

A _r =-- 1 r — I - оператор Лапласа по координате r ;

r д r ^ дr )

1 d k j

Dj =---— - коэффициенты, характеризующие дис- j    2 a® j персию второго порядка j = 1,2; D - коэффициент, характеризующий дифракцию (в выбранной нормировке D = 1); kj, ®j - волновое число и частота волны соответственно j = 1,2; у - коэффициент нелинейной связи взаимодействующих волн; aj - коэффициенты самовоздействия волн j = 1,2; Z - безразмерная длина нелинейной среды; R – поперечный размер нелинейной среды; T – безразмерное время, в течение которого анализируется рассматриваемый процесс.

На входе в нелинейную среду задается распределение импульса:

A ( t , r , z = 0) = A ⁰( t , r ),

B ( t , r , z = 0) = B ⁰( t , r ).

Граничные условия имеют вид

Al t=0T = 0, r — r . = 0, A | r = r = 0, д r

B l,=0,T = 0, r ^ B r . = 0, Bl r = R = 0.

Обобщение итерационного метода M1 к решению многомерной задачи. В системе (1) сделаем замену переменных C = Be-ikz и получим нелинейную систему уравнений f + DA rA + D ^  A * C +

AiaA (| A |2 +2|C|2) = 0, dC .D , _ _ 82C . ,2 + k^C- + i A C + iD->      + i уA + dz           2 r 2 a t2

+ 2 i a C (2| A |² + 1 C |²) = 0.

Далее произведем замену переменных f^1 = r,

[^2 = t - vz, и получим следующую систему уравнений

• - v   + iD A A + id Ba! +1 уa * C +

6t 2         ^{6 1}         ' 56 2

+ i a A (| A | 2 + 2| C |⁵) = 0,

‘ - v^C + ikC + iDA, C + iD. ⁹2C + d6 2            2 ^{6 1        2} дб 2

+ i Y A ² + 2 i a C (2| A |² + | C |²) = 0.

В системе (4) проинтегрируем первое и второе уравнение по 62 и получим систему

5A vA = iDJ A61 Ad62 + iD1 — +

+ i y J A* Cd 6 ₂ + i a J A (| A |² + 2| C |²) d 6 ₂, v^C = i J kCd ⁶ 2 + iD J ^A 6 1 ^{Cd 6} 2 ^{+ iD} 2 д- C - ⁺ + i y J A ² d 6 ₂ + 2 i a J C (2| A |² + | C |²) d 6 ₂.

Задачу (5) будем решать разностным методом в области G = {-L <61 < L, -L < 62 < L}. Величина L подбирается экспериментально из соображений сохранения первого инварианта. Далее вводим равномерную сетку с числом узлов N х N, а исходные начальные приближения размерности N х N представляем в виде вектора размерности N2 , упорядо- ченного по столбцам. Далее для системы (5) запишем итерационный процесс:

Итерационный процесс (6) прекращает свою работу, когда будет выполнено условие

A n* ^{+ 1}

( - j           A "

= A”+т _^A^1 A”h2 + i_ -j v k=1

^^^^^^»

h ₂

n

j +

v " + 1 - v "	< s .
vn

jj

+i/V(A”)*C”h2 + ia£A”(I A” I2 +2|C” |2)h2 k=i

( jj

IC”+1 = C” + I iky C”h + i_у A C”h + j j I    z—f m 2     -) z—i Si k 2

V m=1

C" -C" , j

+ _2 Cj-Cj-2 + iyV (A”+1)2 h2 + h2

j]

+ 2 ia^ C” (21 A”+1 |2 +|C"|2)h2 I, k=1

где

AS Aj = T2    (S j+0,5 Aj+1 - h S j

- ^{( S} j +0,5 ^{+ S} j -0,5 ) ^Aj ^{+ S} j -0,5 ^Aj -1 ),

A 0 , C° - задаются изначально, v" ^{+ 1} вычисляется по следующей формуле:

v

," + 1 = 1 1 ( A_" ^{+ 1}, A " ) - 1 ] т^ ( A " , A " )      J ^.

Результаты расчетов. В качестве начальных приближений A ⁰, C ⁰ для действительной и комплексной части брались функции вида «домик» (рис. 1) и функция «параллелепипед» (рис. 2) или функция «двойной домик» (рис. 3) для получения солитонного решения второй моды.

Расчеты производились при следующих значениях управляющих параметров: _ 1 = 0,08, _ ₂ = 0,14, _ = 0,1, a = 5, y = 20 . Шаг по пространству h 1 = h ₂ = 0,02 , параметр т подбирается экспериментально, в данном случае т = 10 ^{- 5}. Результат работы метода изображен на рис. 4, а распределение фазы волны представлено на рис. 5. Время численного расчета составило 40 минут, число итераций "  = 2 521, невязка v = 0,04. Также на рис. 6 приведено солитонное решение второй моды, для которого шаг по пространству был взят h 1 = h ₂ = 0,01, время расчета составило около 5 часов, число итераций "  = 6 725, невязка v = 0,02. Стоит отметить, что для получения солитонного решения второй моды можно использовать в качестве начального приближения функцию «двойной параллелепипед».

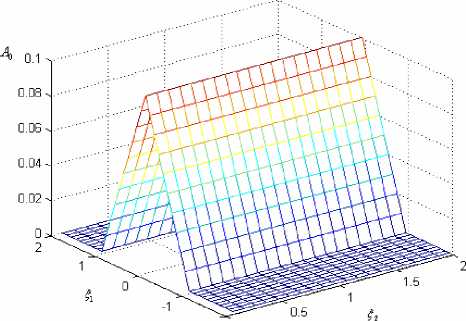
-2 0

Рис. 1.

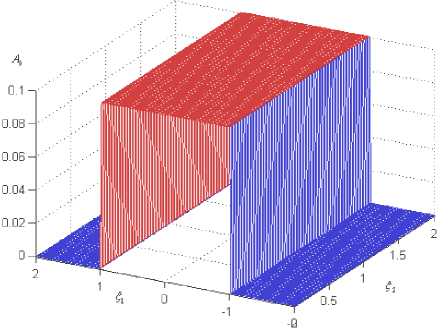
Рис. 2

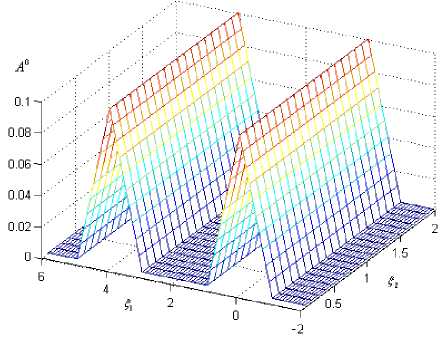
Рис. 3

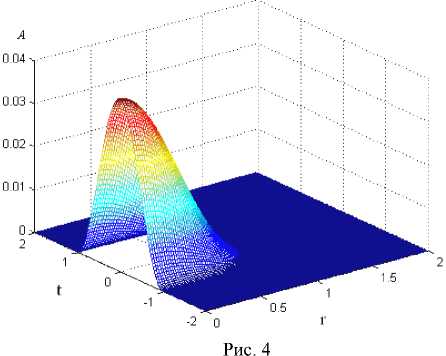
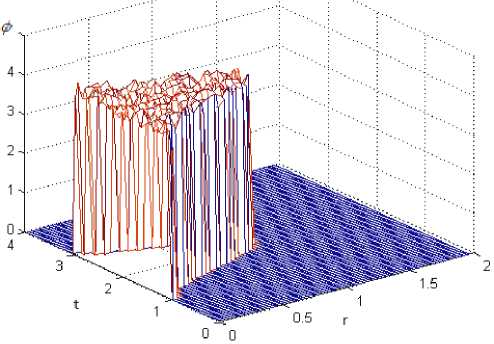
Рис. 5

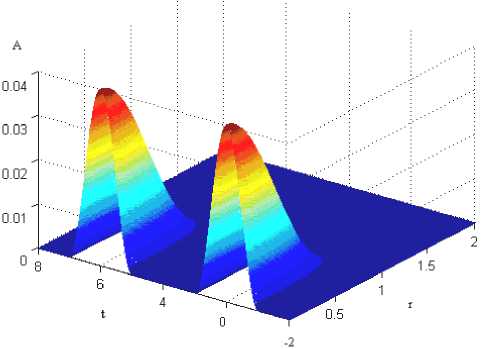
Рис. 6

Дальнейшие численные эксперименты показали, что уменьшение шага по пространству приводит к увеличению времени решения, но и к уменьшению невязки. Также на каждой итерации производится вычисление объема решения, начиная с некоторой итерации, когда солитон сформировался, объем сохраняется до прекращения работы метода, что подтверждает сохранение первого инварианта.

Использование параллельных вычислительных систем. Итерационный метод M1 обладает хорошими параллельными свойствами. Исходную дискретную область разбиваем на равные подобласти и рассылаем эти подобласти по процессорам, что позволяет получить почти 100%-й выигрыш в производительности.

Метод M1 был реализован на многопроцессорных компьютерах с использованием программного средства MPI. Решение исходной задачи методом M1 при h = 0,01 на различных машинах дало следующие результаты:

ПК (1 процессор (1 ядро), общая память) – 140 мин.

ПК (2 процессора (4 ядра), общая память) – 45 мин.

Кластер (16 процессоров (32 ядра), разделенная память) – 8 мин.

Из результатов видно, что 100 % выигрыша в производительности не получается, в силу неравномерной загрузки процессоров и времени на пересылки данных между процессорами.

Обобщение итерационного метода M2 к решению многомерной задачи. По аналогии с применением метода M1, произведем замену переменных

^ 1 = r ,

^2 = t - vz, а полученную систему нелинейных уравнений, используя конечно-разностную аппроксимацию, сведем к системе матричных уравнений вида

V k A n ^{+ 1} = P n ( А П , С П ) A k ^{+ 1},

VnCk+1 = Qn (An+1, СП) cn+1, где Pn и Qn - матрицы размерности N2 x N2, полученные из (6) Akn – k-й собственный вектор длины N2 ; vkn – соответствующее собственное значение.

Алгоритм M2 для данной системы будет выглядеть следующим образом

• 1)    по A_kⁿ и C_kⁿ строим матрицу Pⁿ ;

• 2)    находим собственное значение v k ^{+ 1} и собственный вектор А П ^{+ 1} матрицы P ” ;

• 3)    по А П ^{+ 1} и С П строим матрицу Q n ;

• 4)    находим собственное значение v k ^{+ 1} и собственный вектор С П ^{+ 1} матрицы Q n ;

• 5)    сравниваем результаты на данной и предыдущей итерациях.

A ⁰, C ⁰ – задаются изначально. Метод прекращает свою работу, когда будет выполнено условие

I v k ^{+ 1} - v k .

Результаты расчетов. В качестве начальных приближений используются функции изображенные на рис. 1 и 2. Расчеты производились при следующих значениях        управляющих        параметров:

D 1 = 0,08, D ₂ = 0,14, D = 0,1, a = 5, y = 20. Шаг по пространству h 1 = h ₂ = 0,1, параметр т подбирается экспериментально, в данном случае т = 10 ^{- 5}. Результат работы метода изображен на рис. 7. Метод завершил работу за 15 минут, произведя 27 итераций, невязка составила 0.13, распределение фазы волны соответствует рис. 5. Отметим также, что если в ходе итерационного метода M2 рассматривать второе собственное значение и соответствующий ему собственный вектор, то можно получить солитонное решение второй моды, аналогично для k -й моды.

Таким образом, в настоящей работе предложены два итерационных метода нахождения солитонных решений для системы двух нелинейных уравнений Шредингера, описывающей процесс генерации второй гармоники в среде с кубичным откликом в трехмерной постановке в аксиально-симметричном случае. В отличие от численного метода решения, описанного в [7], который подразумевает некоторые преобразования, обусловленные видом нелинейности, методы M1 и M2 не требуют никаких дополнительных

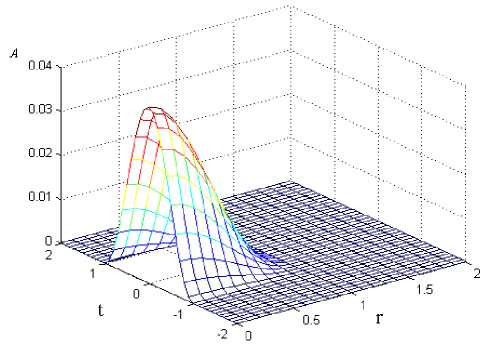
Рис. 7

преобразований и могут быть применимы по стандартной схеме, описанной в [5; 6], что значительно упрощает решение задачи. Особенностью методов M1 и M2 является сходимость к солитонному решению для любых начальных приближений, схожих с описанными выше, что позволяет обойти проблему выбора начального приближения, которую не удается так легко избежать в работе [7].

Для решений задачи (1) на сетке, предложенной выше с шагом h = 0,01 на ПК, методу M1 требуется около двух часов, а методу, предложенному в [7], требуется более суток. Метод выигрывает в 10 раз на ПК, а если использовать параллельные вычислительные системы, то можно добиться выигрыша в несколько сотен раз. Если учесть, что данную задачу необходимо решать для большого количества значений управляющих параметров a , у, чтобы найти область существования солитонных решений, то метод M1 с использованием параллельных вычислительных систем позволит найти область за несколько дней, в зависимости от области и шага.

В заключение отметим, что предлагаемые методы M1 и M2 можно успешно использовать при математическом моделировании оптических компьютеров. Возникающие при определенных значениях управляющих параметров солитонные решения, сохраняющие форму, соответствует сохранению формы сигнала [4]. Отсутствие солитонного решения (нарушение сходимости методов) соответствует потере сигнала, т. е. сбою передачи данных в оптическом компьютере.