Численное исследование многопустотных панелей перекрытия различных длин

Пустотные плиты представляют собой сборные конструкции из напрягаемого или ненапря-гаемого бетона, обычно используемые при строительстве полов в многоэтажных жилых зданиях. Особую популярность такие плиты имели в странах Северной Европы, а также бывшего Советского Союза. Популярность сборного железобетона актуальна в первую очередь для зон с небольшой сейсмичностью. Также применение сборных железобетонных панелей характеризуется экономичностью из-за быстрой сборки зданий и уменьшения собственного веса конструкций. Сборная железобетонная пустотная плита имеет трубчатые пустоты, проходящие по всей длине плиты, обычно с диаметром, равным примерно двум третьим или трем четвертым толщины плиты. Это делает плиту намного легче, при этом увеличивается полезная нагрузка и снижаются материальные и транспортные расходы. Такие плиты обычно имеют ширину в среднем 1200 мм и стандартную толщину обычно от 150 до 500 мм.

Стальная арматура в растянутой зоне плиты обеспечивает сопротивление изгибу.

Основное преимущество пустотных панелей – сравнительно небольшой вес, позволяющий увеличивать полезную нагрузку на перекрытия или использовать более длинные перекрытия для больших пролетов. При этом некоторые авторы предлагают новые конструкции пустотных плит с более легкими и экологичными материалами. Такими свойствами, например, обладают плиты системы «Cobiax», испытанные и предложенные в работе [1]. В труде А.А. Аль-Аззави и С.А. Абед [2] выполнено исследование поведения железобетонных пустотных плит с различными физикомеханическими и геометрическими характеристиками. Исследовалась прочность пустотных плит на сдвиг. Были проведены натурные эксперименты и соответствующие нелинейные расчеты методом конечных элементов (МКЭ), чтобы доказать, что прочность на сдвиг многопустотных плит составляет не менее 50 % от сдвиговой прочности аналогичной сплошной плиты.

Исследование плит перекрытия численными методами, в том числе МКЭ, с использованием теорий механики железобетона было выполнено российскими исследователями Н.И. Карпенко [3, 4], С.Ф. Клованичем [5, 6]. На основе моделей механики железобетона, разработанных и описанных вышеназванными исследователями, с применением современных программных комплексов и численных методов поведение железобетонных плит под нагрузкой исследовал А.С. Васильев [7–9]. М.Ф. Джавед и др. [10] в своей работе исследовали эффективность работы стальных, заполненных бетоном, труб. Многие авторы, такие как Юаньли Ву [11], Г.М. Чен [12], М.Л. Беннегади [13], исследовали методы усиления многопустотных плит на основе композитов. Напряженное и деформированное состояние железобетонных плит с предварительно напрягаемой арматурой представлено в исследованиях П. Канкери [14], Аль-Негхаймиш [15], В. Альберо [16]. В работе Канкери большое внимание уделялось усилению многопустотных плит после образования трещин в бетоне.

Известно, что для упрощения расчетов пустотных плит и представления их в форме стержневых балочных конечных элементов используется именно двутавровая форма. В рамках теории расчета железобетонных конструкций, учитывается не только наличие арматуры внутри бетона (т. е. наличие армирующего материала внутри армируемого), но также и перераспределение усилий между этими материалами при появлении трещин и разрушении бетона. При этом геометрические параметры сечения также могут оказывать влияние на результаты расчетов железобетона при перераспределении усилий и образовании пластического шарнира в конструкции.

Материалы и методы

В работе рассматриваются многопустотные плиты перекрытий различных длин, взятых по ГОСТ 9561-91. За основу исследования приняты стандартные панели: высота 220 мм, круглые пустоты диаметром 159 мм. Ширина была принята фиксированной и составила 1000 мм. Данный тип плит перекрытий предназначен для опирания по двум сторонам. При численных расчетах рассматривалось 9 × 2 вариаций плит в зависимости от длины. Эти вариации приведены в табл. 1.

Материалы: бетон тяжелый класса В25 (Eb = = 3·104 МПа, Rbt = 1,05 МПа, Rb = 14,5 МПа); рабочая продольная арматура А400 (Rs = 365 МПа, Es = 2·105 МПа) – 6 стержней диаметром по 12 мм. Защитный слой бетона 30 мм. Сечения рассматриваемых образцов приведены на рис. 1.

Таблица 1

Рассматриваемые образцы

№	Длина, мм	Естественная форма	Форма двутавровых балок
1	2400	Образец 1.1	Образец 1.2
2	2700	Образец 2.1	Образец 2.2
3	3000	Образец 3.1	Образец 3.2
4	3300	Образец 4.1	Образец 4.2
5	3600	Образец 5.1	Образец 5.2
6	3900	Образец 6.1	Образец 6.2
7	4200	Образец 7.1	Образец 7.2
8	4500	Образец 8.1	Образец 8.2
9	4800	Образец 9.1	Образец 9.2

Рис. 1. Геометрические характеристики панелей: a – поперечное сечение панели в естественной форме, б – поперечное сечение панели в форме двутавровой балки, в – типичная расчетная схема плиты

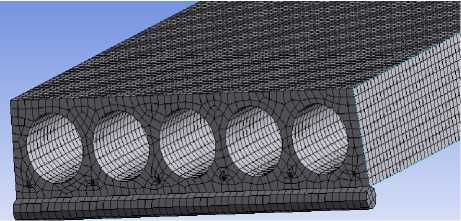
Расчеты выполнены в программном комплексе ANSYS 19R2. Дискретные модели насчитывали от 70000 до 150000 ячеек и от 100000 до 200000 узлов в зависимости от типа сечения и длины образца (рис. 2). Конечные элементы - в форме гексаэдра, максимальный размер 20 мм. Для уменьшения концентрации напряжений по краям, были смоделированы круглые опоры в местах опирания.

Каждый образец при проведении численного эксперимента последовательно нагружали, начиная от нулевой нагрузки, с шагом нагрузки AF = 1 кН, до разрушения, происходившего от действия изгибающего момента в середине пролета образцов, при достижении предела текучести арматурой в растянутой зоне. На каждом шаге нагрузки получали соответствующий ей прогиб. Поведение бетона моделировалось на основе крите- рия прочности Willam-Warnke [17], на основе конечного элемента SOLID 65. На основе использованной модели, трещины образовывались по площадке, нормальной к главным напряжениям, при превышении ими заданного предела прочности при растяжении. Также учитывалось объемное напряженное состояние.

Результаты и их обсуждение

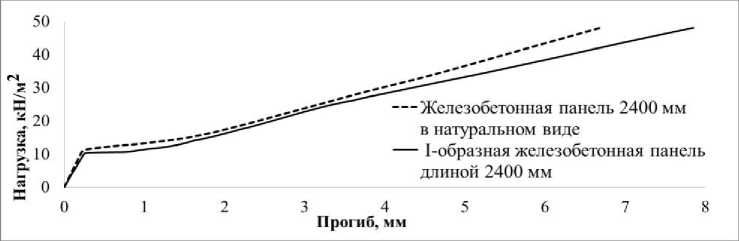
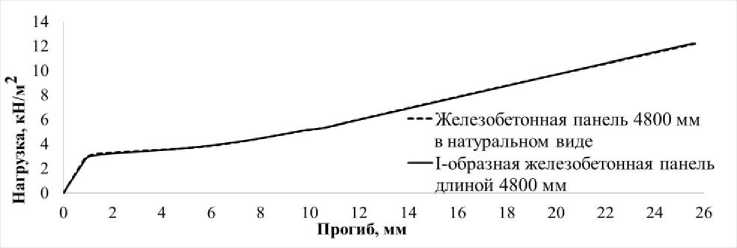
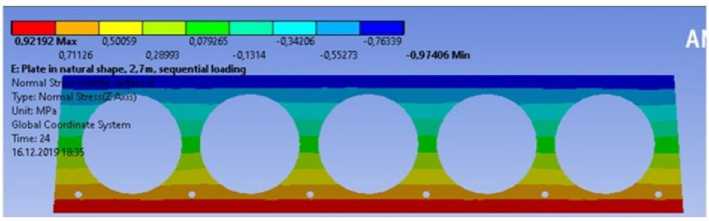
Из рис. 3 видно, что с увеличением длины образцов графики нагрузка - прогиб коррелируют значительно сильнее. Также на графиках можно заметить, что при сопоставлении более коротких образцов появление трещин у образцов в двутавровой форме наступает раньше. Это подтверждается рис. 4, где представлены изополя напряжений в образцах при численных расчетах.

а)

б)

Рис. 2. Конечно-элементная сетка плит (ANSYS): а – естественная форма, б – двутавровая форма

а)

б)

Рис. 3. Сравнение результатов расчетов отклонения нагрузки для образцов в виде двутавровых и естественных сечений: а – образцы длиной 2400 мм, б – образцы длиной 4800 мм

а)

б)

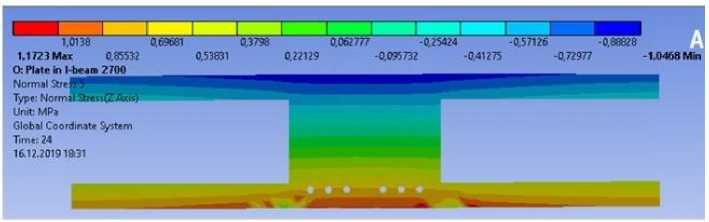
Рис. 4. Изополя распределения нормальных напряжений в срединном сечении образцов при нагрузке 9,163 кН/м2: а – образец 2.1, б – образец 2.2

На графиках ниже представлены основные результаты исследования. На рис. 5 представлена нагрузка трещинообразования для образцов различных длин. Здесь по оси ординат представлены величины разрушающих нагрузок для каждого образца, а по оси абсцисс непосредственно соответствующие длины каждого из образцов. Как можно заметить, с увеличением длины образцов для всех трех видов расчетов отклонения между результатами уменьшаются, а результаты коррелируют лучше. То же самое можно увидеть в табл. 3, где представлены отклонения результатов.

На рис. 6 представлены результаты макси- мальных прогибов для образцов различных длин. Как видно, на образцах меньшей длины результаты лучше коррелируют между собой для аналитического расчета и расчета плиты в естественной форме (ANSYS). Однако при длине большей чем 3600 мм результаты расчетов ANSYS для двутавровой и естественной формы начинают лучше коррелировать между собой, а для длин 4500 мм и 4800 мм – практически совпадают.

Из рис. 7 видно, что результаты аналитического расчета по несущей способности слабо коррелируют с результатами численных (ANSYS). Основные результаты расчетов многопустотных плит представлены в табл. 2.

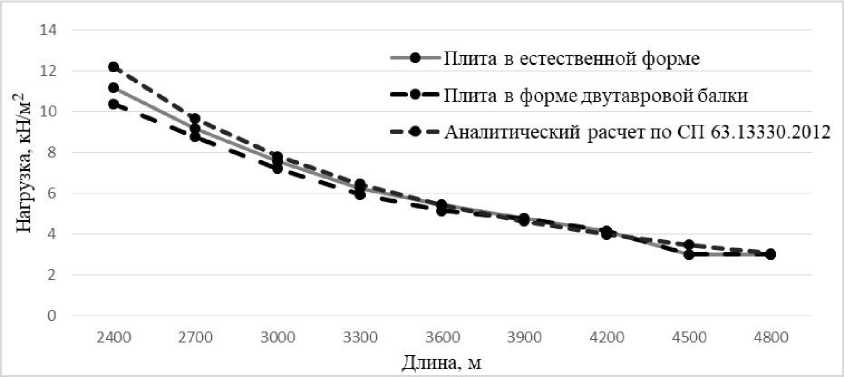
Рис. 5. Нагрузка трещинообразования образцов различных длин для естественной формы многопустотных панелей (ANSYS), панелей в двутавровой форме (ANSYS), панелей, рассчитанных аналитически по нормативным документам

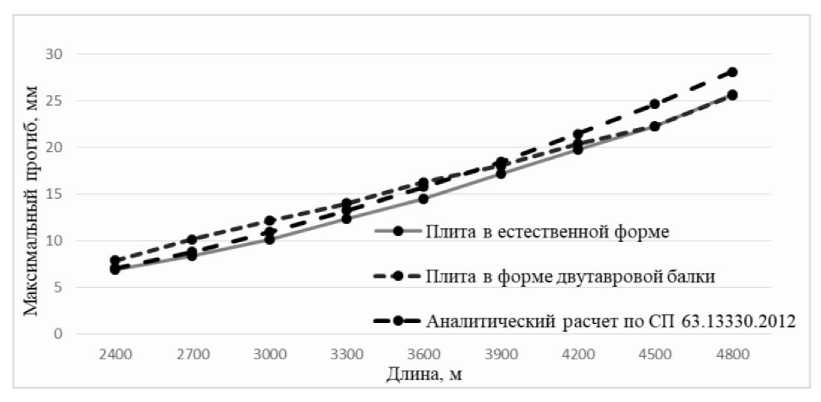
Рис. 6. Максимальные прогибы образцов различных длин для естественной формы многопустотных панелей (ANSYS), панелей в двутавровой форме (ANSYS), панелей, рассчитанных аналитически по нормативным документам

Рис. 7. Разрушающая нагрузка образцов различных длин для естественной формы многопустотных панелей (ANSYS), панелей в двутавровой форме (ANSYS), панелей, рассчитанных аналитически по нормативным документам

Результаты расчетов многопустотных панелей

Таблица 2

Тип панели, вид расчета	Образцы плит	Шаг загрузки при появлении трещин, №	Нагрузка образования трещин кН/м2	Максимальный прогиб, мм	Разрушающая нагрузка, кН/м2
1	2	3	4	5	6
Плита в естественной форме	Образец 1.1	26	11,16838488	6,8756	49,39862543
	Образец 2.1	24	9,163802978	8,3601	38,18251241
	Образец 3.1	22	7,560137457	10,084	30,58419244
	Образец 4.1	20	6,248047485	12,282	25,61699469
	Образец 5.1	19	5,441008018	14,485	21,47766323
	Образец 6.1	18	4,758128469	17,115	18,50383294
	Образец 7.1	17	4,172803142	19,734	15,95483554
	Образец 8.1	15	3,006872852	22,272	13,74570447
	Образец 9.1	14	3,006872852	25,652	12,24226804

Окончание табл. 2

1	2	3	4	5	6
Плита в форме двутавровой балки	Образец 1.2	24	10,395189	7,851	48,10996564
	Образец 2.2	23	8,781977854	10,123	39,70981291
	Образец 3.2	21	7,216494845	12,115	32,3024055
	Образец 4.2	19	5,935645111	13,959	26,55420181
	Образец 5.2	18	5,154639175	16,216	22,6231386
	Образец 6.2	18	4,758128469	17,977	19,29685435
	Образец 7.2	17	4,172803142	20,342	16,44575356
	Образец 8.2	15	3,006872852	22,234	13,74570447
	Образец 9.2	14	3,006872852	25,556	12,24226804
Аналитический расчет по СП 63.13330.2012	Образец 1.2		12,22222	7,0	62,5
	Образец 2.2		9,657064	8,8	49,3
	Образец 3.2		7,822222	10,9	40
	Образец 4.2		6,464646	13,2	33,05
	Образец 5.2		5,432099	15,7	27,8
	Образец 6.2		4,628534	18,4	23,7
	Образец 7.2		3,99093	21,4	20,4
	Образец 8.2		3,476543	24,6	17,8
	Образец 9.2		3,055556	28,1	15,6

В табл. 3 представлены отклонения результатов расчетов для нагрузки образования трещин, предельных прогибов и разрушающих нагрузок. За эталон приняты плиты с естественной формой сечения.

Как видно из табл. 3, отклонение момента трещинообразования для различных образцов составило в среднем около 2,8 %, отклонение максимальных прогибов – приблизительно –10,84 %; а отклонение в разрушающей нагрузке – около 4,3 %. Для выявления степени общей зависимости графиков нагрузка – прогиб плит разных длин был использован метод статистического исследования – корреляционный анализ.

Из табл. 4 видно, что результаты аналитических расчетов по СП имеют значительные отклонения от численных.

Для нагрузки образования трещин отклонение расчета по СП от численного с естественной формой сечения плиты показало среднее значение – 3,5 %, при максимальном значении около –15 %.

Таблица 3

Образцы плит	Нагрузка образования трещин, %	Максимальный прогиб, %	Разрушающая нагрузка, %	Общий коэффициент корреляции для соответствующих графиков
Образцы 1.1 и 1.2	6,92	–14,17	2,61	0,997121503
Образцы 2.1 и 2.2	4,17	–21,05	–4,00	0,998304465
Образцы3.1 и 3.2	4,55	–20,14	–5,62	0,998249
Образцы4.1 и 4.2	5,00	–13,65	–3,66	0,999003
Образцы5.1 и 5.2	5,26	–11,95	–5,33	0,999826
Образцы6.1 и 6.2	0	–5,04	–4,29	0,999856
Образцы 7.1 и 7.2	0	–3,08	–3,08	0,999868
Образцы 8.1 и 8.2	0	–5,17	–5,00	0,99991
Образцы 9.1 и 9.2	0	–3,30	–3,51	0,999952

Таблица 4

Образцы плит	Нагрузка образования трещин, %	Максимальный прогиб, %	Разрушающая нагрузка, %
Образцы 1.1 и 1.2	–9,44	–1,81	–26,52
Образцы 2.1 и 2.2	–5,38	–5,26	–29,12
Образцы 3.1 и 3.2	–3,47	–8,09	–30,79
Образцы 4.1 и 4.2	–3,47	–7,47	–29,02
Образцы 5.1 и 5.2	0,16	–8,39	–29,44
Образцы 6.1 и 6.2	2,72	–7,51	–28,08
Образцы 7.1 и 7.2	4,36	–8,44	–27,86
Образцы 8.1 и 8.2	–15,62	–10,45	–29,49
Образцы 9.1 и 9.2	–1,62	–9,54	–27,43

Отклонение результатов численных расчетов образцов в естественной форме от аналогичных образцов в двутавровой

Отклонение результатов численных расчетов образцов в естественной форме от результатов аналитических расчетов по СП 63.13330.2012

Максимальные прогибы при аналитическом расчете во всех случаях преобладают над результатами численного в среднем на 7,5 %. Максимальное отклонение оставило более 10 % для образца длиной 4500 мм.

Из табл. 4 видно, что несущая способность пустотных плит в естественной форме, меньше несущей способности, посчитанной аналитически по СП, в среднем на 29 %.

Выводы

Исходя из полученных данных можно сделать следующие выводы.

С увеличением длины образцов коэффициент корреляции возрастает и стремится к единице, что говорит об усилении связи между графиками нагрузка – прогиб.

С увеличением длины рассматриваемых образцов отклонение в нагрузке появления трещин постепенно уменьшается и для образцов 3900 мм и более сводится к нулю. Однако для плит от 2400 мм до 3600 мм следует результаты расчетов плит в форме двутавра домножать на коэффициент 1,03. Если же выполнять расчет аналитически, согласно нормативным документам, то этот коэффициент составит приблизительно 0,97.

Тенденция отклонения прогибов аналогична ситуации с нагрузкой появления трещин. Однако отклонения в прогибах между образцами имеют достаточно большую разницу. в связи с этим величину прогиба для плит длиной от 2400 до 3000 мм следует умножать на коэффициент 0,85, для плит от 3300 до 3600 мм – на 0,9 и для образцов свыше 3600 мм – на 0,95 с целью уточнения результатов для многопустотных плит двутавровой формы.

Несущая способность в результате аналитического расчета имеет очень большой коэффициент запаса, что приводит к перерасходу материала при проектировании железобетонных конструкций и расчетах по первой группе предельных состояний. Следует провести дальнейшее исследование и разработать коэффициенты, которые бы уточняли расчеты несущей способности пустотных плит. Для плит шириной 1 метр результаты несущей способности, полученные при аналитических расчетах по СП, можно уменьшать в среднем на 30 %. Однако стоит учитывать, что данная нагрузка, проведенная при численном эксперименте в ПК ANSYS, является кратковременной, в то время как расчеты выполняются для длительных нагрузок.