Численное исследование неустойчивости пластического сдвига при динамическом нагружении

Реальные материалы тела обладают сложным структурным строением [1,2,3,4]. В них образуются микродефекты различных типов: точечные, дислокации, двойники, ячеистая, блочная, фрагментированная структура, межзеренные границы и некоторые другие. Основными носителями пластической деформации являются дислокации. Начинается деформация с движения одиночных дислокаций, которые очень слабо взаимодействуют. По мере развития деформации происходит генерация новых дислокаций. Взаимодействие между дислокациями увеличивается, начинают играть роль коллективные эффекты в дислокационном ансамбле. Дислокации при своем коллективном взаимодействии и при встрече с препятствиями создают высокие локальные перенапряжения, которые являются естественной предпосылкой для зарождения и развития микросдвигов и микротрещин – типичных дефектов мезоуровня. По мере накопления микродефектов все большее значение начинает приобретать их взаимодействие между собой. Дальнейший рост концентрации микродефектов усиливает их взаимодействие настолько, что в ансамбле микродефектов проявляются коллективные эффекты [2,3].

Физикой прочности и пластичности накоплен огромный экспериментальный и теоретический материал о строении и структурных процессах в реальных материалах. Одновременно в механике деформируемого твердого тела, имеющей хорошо разработанный аппарат для постановки и решения краевых задач определения напряженно-деформированного состояния материала, становится очевидным ограниченность феноменологического подхода. В настоящее время интенсивно развивается направление, основанное на стремлении синтезировать два вышеуказанных подхода. Теории, учитывающие реальное строение материалов, должны основываться на компромиссе между адекватным описанием структурных процессов и сложностью модели. В связи с этим из многообразия элементов структуры необходимо выбирать те, которые оказывают определяющее влияние на деформационное поведение. Многочисленными экспериментальными исследованиями показано, что важными дефектами структуры, определяющими релаксационные свойства и кинетику разрушения реальных материалов, являются микросдвиги, микротрещины – типичные дефекты мезоуровня. [4–9]. Так, многочисленные структурные исследования процессов высокоскоростного соударения указывают на определяющую роль в явлениях неустойчивости пластической деформации согласованного поведения ансамбля этих микродефектов.

В данной работе построена математическая модель, описывающая основные черты формирования, развития неустойчивости и локализации пластической деформации при высокоскоростном соударении с учетом нелинейного поведения ансамбля взаимодействующих микросдвигов.

Значительное внимание вопросам неустойчивости и локализации пластической деформации уделено в работах научного направления, возглавляемого академиком В.Е. Паниным [1,10,11], в которых развивается представление о деформируемом твердом теле как о многоуровневой системе, в которой пластическое течение развивается как последовательная эволюция потери сдвиговой устойчивости на различных масштабных уровнях: микро, мезо и макро.

Экспериментальные исследования микроструктуры полос адиабатического сдвига, проведенные в ряде работ, в частности [12], ясно указывают на то, что формирование полос адиабатического сдвига является результатом скачкообразных процессов в системе микросдвигов и пластических ротаций и тесно связано с изменением ориентаций зерен в узких полосах сдвига,

Обсуждаемый класс явлений в последние годы исследуется нелинейной физикой [13, 14, 15], рассматривающей данные эффекты с позиций неравновесных ориентационно-кинетических переходов.

В данной работе используется ранее разработанная теория [13], в которой методами статистической физики и термодинамики необратимых процессов изучается влияние микросдвигов на упругие и релаксационные свойства твердых тел. Определяющие уравнения сред с микросдвигами имеют следующий вид:

σ ik ⁼ L 1 e i^pk ^- L 2 p ^& ik , ^Π ik ⁼ L 2 e i^pk ^- L 3 p ^& ik . (1)

Здесь pik – тензор, характеризующий интенсивность и преимущественную ориентацию микросдвигов;

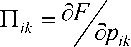
– термодинамическая сила, действующая на систему, когда pik отличается от равновесного ( F – свободная энергия среды с микросдвигами);

σ _ik , e_i ^p _k – тензоры напряжений и скоростей пластических деформаций; L_i – кинетические коэффициенты, зависящие от p_ik . Определяющие уравнения материала (1) включают соотношения релаксационного типа для тензора напряжений и уравнения движения для параметра p_ik . В этих уравнениях учтены "перекрестные" эффекты:

влияние микросдвигов на релаксационные процессы и пластичности на кинетику роста pik . В дальнейшем рассматривается случай, когда пластическая деформация подчиняется условию eipi = 0 (пластическая несжимаемость материала), а среднее напряжение σ=3 σii определяется через упругие составляющие тензора деформаций.

В рамках данной теории были определены характерные реакции материалов на образование дефектов и было сделано предположение, что эффекты неустойчивости пластического сдвига обусловлены ориентационно-кинетическими переходами в ансамблях микросдвигов.

Резкий переход к более упорядоченной дефектной структуре часто приводит к аномалиям деформационных свойств, которые могут проявиться, в частности, при высокоскоростном соударении ударника с преградой (выбивание пробки) [16,17] (рис.1.)

Развитый подход был применен при численном моделировании механизмов неустойчивости, сопровождающихся выбиванием пробки. Для исключения влияния вторичных факторов процесс выбивания пробки рассматривался в упрощенной постановке, и предполагалось, что кинетическая энергия ударника расходуется на деформирование пробки, диаметр которой принимается равным диаметру ударника, и на преодоление сил сопротивления сдвигу в узкой области по образующей пробки.

При решении задачи считаем, что пробка представляет упругий стержень, который по цилиндрической образующей связан с основным массивом тонким деформируемым слоем, поведение которого определяется системой уравнений, описывающих упругопластическую среду с микросдвигами.

Так как ширина области сдвига точно неизвестна, для оценки скорости деформации сдвига в цилиндрической области по периметру ударника у использовалось соотношение

Y = 0,5 v/ R p .                                           (3)

В данной модели принимается аддитивность упругих и пластических скоростей деформаций:

Y = Y e + Y p ,                                            (4)

где Y e , Y p , Y — скорости упругой, пластической и полной деформации, соответственно.

Справедливость условия аддитивности скоростей деформаций обусловлена малостью упругих деформаций и гидродинамическим характером необратимых деформаций.

Уравнения, описывающие поведение релаксирующей среды с микросдвигами, у = 2 Ц( Y - Yp ). т = 11Y p -12 dp, п = 12Yp -13 |p,(5)

оt                             о td где p - компонента тензора плотности микросдвигов, ц - модуль сдвига.

Функция П аппроксимировалась выражением [13]

П = -AiT exp(-Pa I p) + Bi(p - Pb),                           (6)

где A ₁, B ₁, p_a , p_b – параметры аппроксимации.

После перехода к безразмерным переменным имеем т = т I ц; 2 = z I h; % = 11 At; Yp = Yp ' At; v^ = v^11 h ; П = A t П113, где h - толщина пластины, A t = 10-6, в дальнейшем символ (~) для безразмерных переменных опускаем и получаем:

_Y p =HA t . _т+ 1 2 d p

I i a t ’ vh v 2 Rp A t

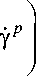
dr= 2

a t до _ E дv д t ц дz

£ д V _S v

V д t ” дz ’ дv ц A t2   v до 2 h т дt    Роh2    [ дz   Rp v где V - относительный объем материала ( V _ р0 / р); р0, р - начальная и текущая плотность материала, о - упругое напряжение в стержне, т - сдвиговое напряжение в цилиндрическом слое, E - модуль Юнга, ц - сдвиговой модуль, v - массовая скорость в стержне, h – толщина пластины, Rp – радиус пробки.

Рассмотрим соударение посредством налетания жесткого ударника, движение которого описывается уравнением динамики твердого тела дv„ п R Р — о (0, t),                         (14)

д t       mph где mp – масса ударника, vp – скорость ударника, Rp – радиус ударника и пробки.

Численно решалась система уравнений (7) – (14). Использовались граничные условия v (0, t ) _ v_p ( t ) при о (0, t ) <  0; о (0, t ) _ 0 при z c ( t ) <  z (0, t ), где z c ( t ) -координата поверхности   ударника, о (1, t ) _ 0    и начальные   условия

v ( z ,0) _о ( z ,0) _ p ( z ,0) _ 0, V ( z ,0) _ 1, z g [0,1], t g [0, да ), v p (0) _ v 0 , где v 0 -начальная скорость ударника.

Численное решение системы проводилось методом конечных разностей.

Результаты численного моделирования представлены на рис.1. В процессе распространения упругой волны по длине пробки происходит деформирование цилиндрического слоя, связывающего пробку с основным массивом материала. В этом слое возникают сдвиговые напряжения, которые приводят к развитию упругих и пластических деформаций и развитию дефектной структуры: росту параметра плотности микросдвигов.

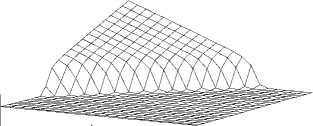
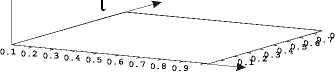
При достижении определенного уровня дефектности в материале происходит ориентационный переход по параметру плотности микросдвигов, обусловленный скачкообразным ростом уровня дефектной структуры, происходящим последовательно в каждом поперечном сечении цилиндрического слоя (рис. 2, а), что в свою очередь приводит к резкому росту скоростей пластических деформаций в этих сечениях (рис. 2, б) и к быстрой релаксации сдвиговых напряжений (рис. 2, в). В результате чего сопротивление материала сдвигу в цилиндрическом слое, соединяющем пробку с основным массивом материала, резко падает, что при достижении волной тыльной поверхности мишени ведет к отделению пробки от остального материала. Такой сценарий образования пробки может иметь место при ударе с достаточно высокой скоростью, при котором образовавшаяся волна напряжений несет достаточно большую энергию, которая может обеспечить формирование пробки в прямой волне нагрузки.

Процесс выбивания пробки можно представить состоящим из двух стадий [18,19]. Первая стадия, связанная с образованием поверхности сдвига, соизмерима с временем распространения волн нагрузки по толщине пластины. Длительность второй стадии, связанной с движением пробки как единого целого, может быть многократно больше.

Исследования проводились при частичной поддержке гранта РФФИ 02–01–00736, проектов МНТЦ № 1181 и № 2146.

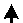
z

tp

z

.

γ ^p

0.25

0.2

0.15

0.1

0.05 0

Рис.1. Схема нагружения

0.07

0.06

0.05

0.04

0.03

0.02

0.01

z

а

0.01

0.005

z

t

τ

0.9

t

бв

Рис. 2. Распространение пластической сдвиговой неустойчивости в процессе продвижения упругой волны по длине пробки: а) плотность микросдвигов p ;

б) скорость сдвиговой пластической деформации γ & ^p ; в) сдвиговое напряжение по образующей пробки τ