Численное исследование параметрических свойств решений некоторого уравнения типа Штурма-Лиувилля

Задача описания распространения электромагнитной волны (ЭМВ) в среде с изменяющимися материальными параметрами (диэлектрической и магнитной проницаемостями) является актуальной в связи с развитием устройств современной фотоники. Например, в работе [1] рассматривался случай константной магнитной проницаемости и линейной (и экспоненциальной) диэлектрической проницаемости; в формализме напряженностей поля < E, B >  найденное решение выражалось через функции Бесселя. При этом авторы даже учли протекание в среде токов.

Ранее в [2] мы вывели для плоской волны, распространяющейся в нестационарной среде, систему дифференциальных уравнений (в формализме потенциалов), в общем виде связывающую электромагнитные потенциалы с управлениями, т.е. парой динамически меняющихся проницаемостей среды е = е (t) , ц = ц(t). Системы уравнений Максвелла мы свели к нескольким однотипным телеграфным уравнениям, а затем методом разделения переменных получили обыкновенные дифференциальные уравнения, которые формально классифицируются как частный случай уравнения Штурма–Лиувилля:

-^Tx + q ( t ) x = w ² x, t E [0; T ] , dt ²

x E [0; L ] .

Однако вопросы ставятся не для краевой задачи Штурма–Лиувилля, а для задачи Коши. В большей степени нас интересуют не глобальные свойства решения, такие как количество нулей на отрезке, а локальные свойства на правом конце отрезка. Такая постановка задачи актуальна для приборов фотоники [3], использующих интерференцию волн в качестве механизма обработки информации.

Там же в [2] мы представили методику нахождения локальных амплитуды, фазы и частоты ЭМВ. Таким образом, каждой дифференциальной задаче Штурма–Лиувилля, выделенной конкретными значениями параметров нестационарности, можно поставить в соответствие тройку введенных нами величин и исследовать уже поведение данной функции.

Хотя и на качественном уровне, нами будет проведен анализ зависимости фурье-образа решения дифференциальной задачи от способа и величины возмущений е = е ( t ) ,ц = ц ( t ). Для ряда численных результатов указана непосредственная связь с теоретическими результатами, полученными в [2]. Преимущественный метод исследования – численный, но в конце статьи мы сделаем попытку аналитически объяснить ряд эффектов.

2.    Общая постановка задачи

Целью работы является параметрическое исследование задачи Коши для уравнений вида [4] Штурма–Лиувилля:

та < \    (( е ) ²    е'   к ² с ²\                 „       /( ц ) ²    ц'   к ² с ²

T j ⁽ t ⁾ ЧУ- ^- Те ⁺      T 1-⁽ t )=⁰ ■  T " ⁽ t )⁺ № ^- 2 ц ⁺ " ц) T 0 ⁽ t ⁾=⁰ •   ⁽¹⁾

Индекс 0 относится к скалярному потенциалу, а 1-к векторному ( j = 1 , 2). Считаем, что w = кс/^е (0) ц (0) , c – скорость света, которую принимаем за 1, поскольку универсальные константы ε 0 ,μ 0 тоже приняты за 1.

Будем рассматривать три модели, которые наиболее естественно бы моделировали нестационарности среды – линейную (а), экспоненциальную (b) и гармоническую (c):

• ( a )    : е ( t ) = е (0)(1 + at ) , ц ( t ) = ц (0)(1 + bt ) ,

• ( b )    : е ( t ) = е (0) exp( -at ) , ц ( t ) = ц (0) exp( -bt ) ,

• ( c )    : е ( t ) = е (0) ^ 1 +— sin pt^ , ц ( t ) = ц (0) ^ 1 +— sin pt^ ,... ; p ^ w.

Проведем процедуру обезразмеривания. Нормируем время на период невозмущенной волны t = —. Примем без ограничений общности с учетом вида (1) е (0) ц (0) за единицу, т.е. нормируем проницаемости на их начальные значения. Соответственно коэффициенты a, b, p будут иметь размерность обратных секунд. Тогда уравнения (1) примут следующий вид, не содержащий ω :

∂ 2 T 1 j dt 2	+ (412 ( Е‘	_ £ д 2 е 2 е d t 2 +	(2 п ) 2 V E, ч - j <  t )=° ■
∂ 2 T 0 dt 2	+ ( 4ц ($) '	1 д 2 ц 2 ц dt 2 +	<2 п £ ) T 0 ( t) = 0 . εμ	(2)

е (0) = 1 ,ц (0) = 1 ,t E [0; N ] .

Без ограничения общности примем ( j = 1 в (2)) граничные условия на левом конце равными (3):

T 11 (0) =0 T 1 (0) = 1 ,

T о (0) = 0 ,t Q (0) = 1 .

Таким образом, получаем математически рафинированную формулировку задачи (2) – (3). В дальнейшем проницаемости интересуют нас как безразмерные коэффициенты, зависящие от некого параметра. Для удобства и дальше будем именовать их проницаемо- стями, которые зависят от времени.

Достаточно решить лишь одно уравнение, для определенности выберем первое из (2), содержащее производные ε по t и, соответственно, граничное условие из первого соотношения в (3). В отсутствие нестационарности его решением будет T ( t ) = — sin(2 nt ).

2 п

3.    Используемые численные методы

Для дифференциальных уравнений используем решатель ode45 в MATLAB. Он является одношаговым явным методом Рунге-Кутты 4-го порядка [5]. С помощью параметра odeset устанавливаем допуски ошибок (10 - ⁵ ) [6]. На промежутке времени шаг сетки составляет 0 . 001, интервал изменения независимой переменной - от 0 до N (Приложение, line 1–3).

Сравним в случае невозмущенной волны решение и производную, выдаваемые ode45 , в начальный и конечный момент времени: T end — T о = 0 . 0002; T end — T Q = — 0 . 0013.

Итак, за 100 периодов не произошло существенного накопления погрешности, что говорит о пригодности данного численного метода для нашей задачи. Общее число точек по оси времени - M t = 10 5 .

Для разложения решения уравнения T ( t ) в ряд Фурье используем функцию fft (Fast Fourier Transform, FFT) в MATLAB. Посредством этой функции производится преобразование (в нашем случае прямое) Фурье для одномерного массива длиной M с применением (4):

M

F ( k ) = ^ T ( j ) ^Ш М- ¹⁾⁽ k- 1) , k = 1 ^: M, ^ш м = exp( - 2 ni ) /M.            (4)

j =1

В результате преобразования Фурье получают [7] комплексные значения, дающие результаты для амплитуды и фазы. На оси частот это выражается тем, что вместо одного пика для тестовой гармоники появляются два симметричных, отвечающих за отрицательные и положительные значения частот, однако нам достаточно рассмотрения одного из них. В MATLAB для FFT используется алгоритм Кули–Тьюки, согласно которому преобразование Фурье от M = M 1 M 2 рекурсивно упрощается до преобразований более малых размерностей M 1 и M 2 . В простейшем случае происходит деление надвое, поэтому M должно являться степенью двойки, а преобразование будет происходить особенно быстро [5, 8]. В нашем случае это M = 2 ¹⁰ (количество точек по оси частот и одновременно по оси времени). Это значение должно коррелировать с утверждением теоремы Котельникова о том, что частота сигнала должна быть в два или больше раз меньше частоты дискретизации

M t

^Fs = N = ¹⁰ 3 .

Так как после решения задачи Коши (2) – (3) имеем M _t точек, то интерполируем решение уравнения на M точек (Приложение, line 4). Для удобства и наглядности смещаем нулевую частоту в центр спектра с помощью функции fftshift [6] (Приложение, line 5).

Калибруем ось k так, чтобы максимальное значение было равно половине частоты дискретизации, для этого вычитаем и получаем значения на оси от - до (далее рассматриваем только положительные значения на оси), после чего растягиваем ось и получаем откалиброванную ось частот Q (Приложение, line 6) с тем, чтобы для невозмущенной волны ~ sin(2 п Q t ) спектральная плотность была сосредоточена на частоте Q = 1. В нашем случае Q £ [0; Q _max = 5 . 12], а точки расположены на этом интервале однородно.

В дальнейшем будем графически отображать зависимость спектральной плотности W (Q). Также будем анализировать зависимости амплитуды P и фазы Q в конечной точке от коэффициентов, отвечающих за нестационарность ( a, b,p ). Поиск проводился по следующей схеме, описанной в [2].

Вводились локальные амплитуды и частоты ( P, ш ) _t — у аргумента тильду писать не будем. Ограничивающим предположением методики является многоэкстремальность кривой T ( t ). Набег фазы считается от точки ближайшего (слева) к -го экстремума и равен произведению локальной частоты на разницу времен, текущего и локального экстремума: Q ( t ) = Ш k ( t — t k ) £ [0; п ] , к : ( t k < t ) Д( t — t k < п ). Аргументы экстремумов при численном решении ищем приближенно из условия y ( i ) y ( i + 1) <  0, где y = T ' ( t ) — предоставляемый ode 45 вектор, а i - номер узла. В конце каждого периода введем значения амплитуды π

Pk = P(tk) = |T(tk) | и частоты Шк = --------. Величины Шk близки по смыслу к частоте tk - tk-1

следования нулей в задаче Штурма–Лиувилля. Для простоты не будем маркировать последнюю точку индексами, относящимися к паре ( P, Q ) _t = _t k . k =_max(k) - Такой анализ назовем «концевым».

Опишем также методику анализа результата преобразования Фурье, т.е. спектральной плотности W(Q), которая во всех рассмотренных нами случаях имела форму волново

го пакета (ВП). Предположим, что при разложении Фурье Q £ [0; Q _max ] и рассмотрим первообразную V (Q) = Jg ^max W (Q) d Q. Введем для некоторого 0 C z C 1 определение

Q z = Q : ( V (Q) /V (Q _max ) = z ). Тогда введем три характеристики ВП: к i = Q 1 / 2 — 1 - цен

троид, К 2 = Q 9 / 10 — Q ₁ / ₁₀ - ширину, К 3 =

W max ^- W min

W max + W min

^ W ^max , min

max , min ^ 1 J 1o C ^ C ^ 9 J 10

W (Q)

– видность (см. «видность» в оптике [5]). Поскольку исходными данными являются ко-

нечномерные вектора, то при численной реализации в MATLAB интегрирование заменяем простым суммированием, а равенство – двумя условиями <,> с последующей линейной интерполяцией.

Сводные результаты анализа фурье-разложения по описанной методике, исключая гармонический случай, приведены в табл. 1.

Примечание. На отрезок [0;1] на частоту Q приходится 100 точек, т. е. числовая погреш ность W(Q) не менее 0.01. В строках Q приведена номинальная частота в конце отрезка, т.е.

( У)

T" + Q( t ) ² T = 0 , Q 2 = Q( t = N ). В строках к 2 приведены соответственно ширина

ВП, граничные частоты Qi/10, Q9/10 и число точек, вошедших в пределы ВП (указываем, как точно нами охарактеризован ВП).

4.    Исследование линеаризованной модели

В первую очередь целесообразно исследовать линеаризованную модель нестационарно-сти. Она является общей, поскольку при разложении в ряд Тейлора проницаемостей на малых временах все частные случаи (1) сводятся к (5):

(^ У dT + ⁽1 + at) T (*) = 0 ,

\ 2 п / dt ²

T (0) = 0 , T ' (0) = 1 , t C N.

Таблица1

Зависимость характеристик ВП от безразмерных параметров нестационарности α ≡ ,β ≡ ωω

		Параметр α
		0.0001	0.0063	0.0125	0.0376
Линеаризованный случай	Ω	1	1.28	1.5	2.19
	κ 1	0.0023	0.1404	0.2534	0.5937
	κ 2	0.0182 (1.0060, 1.0160), 2 точки	0.2135 (1.0360, 1.2562), 22 точки	0.3896 (1.0660, 1.4564), 39 точек	0.9447 (1.1261, 2.0770), 95 точек
	κ 3	0.5490	0.1990	0.2728	0.2492
Параметр α		0.0001	0.0063	0.0125	0.0376
Линейный α = β	Ω	1	0.613	0.44	0.21
	κ 1	–0.0012	–0.2578	–0.4230	–0.7088
	κ 2	0.0203 (0.9960, 1.0160), 2 точки	0.2890 (0.6456, 0.9359), 29 точек	0.3720 (0.4755, 0.8458), 38 точек	0.3391 (0.2252, 0.5656), 34 точки
	κ 3	0.8080	0.6074	0.7760	0.8842
Параметр α		0.0001	0.0032	0.0063	0.0099
Линейный α = -β	Ω	1	1.056	1.288	7.088
	κ 1	0.0010	0.0157	0.0494	0.0951
	κ 2	0.0083 (1.0060, 1.0060), 1 точка	0.0415 (1.0060, 1.0460), 5 точек	0.1989 (1.0060, 1.2062), 20 точек	0.6800 (1.0160, 1.6967), 68 точек
	κ 3	0	0.5303	0.8041	0.9616
Параметр α		0.0001	0.0063	0.0125	0.02
Экспоненциальный α = β	Ω	1	1.88	3.49	7.4
	κ 1	0.0087	0.3070	0.5574	0.7622
	κ 2	0.0203 (1.0060, 1.0260), 2 точки	0.6700 (1.0660, 1.7367), 67 точек	1.7127 (1.0961, 2.8077), 171 точка	2.9292 (1.1161, 4.0490), 292 точки
	κ 3	0.8067	0.6065	0.8039	0.9829
Параметр α		0.0001	0.0063	0.0125	0.02
Экспоненциальный β = - 2 α	Ω	1	0.53	0.286	0.135
	κ 1	0.0009	–0.1538	–0.3029	–0.4605
	κ 2	0.0088 (1.0060, 1.0060), 1 точка	0.2029 (0.7657, 0.9659), 20 точек	0.3531 (0.5756, 0.9259), 35 точек	0.4487 (0.4054, 0.8558), 45 точек
	κ 3	0	0.4847	0.5745	0.7313

Мы будем исследовать (рис. 1) зависимости амплитуды и фазы конечной точки от коэффициента нестационарности α , а также фурье-разложение решения (5). Известно аналитическое решение (7) через функции Эйри [2].

Анализ табл. 1 при α = 0.0001 указывает нам на погрешность численного метода по оси частот – ≈ 0.01 (критерий κ2). ВП локализуется справа от центральной частоты невозму- щенной волны. Наблюдается симметрия ВП относительно центроида. При малых значениях коэффициента нестационарности амплитуда максимального пика, т.е. max W(П), резко падает, затем ее изменения незначительные (рис. 1). Номинальная частота, положение центроида и ширина пика практически линейно пропорциональны α (см. табл. 1). Видность ВП слабо зависит от α и равна примерно 1/4. На абрисе спектральной плотности появляются биения, размах и число которых зависят от α. Экспериментальных данных недостаточно по точности и количеству, чтобы экстрагировать аналитическую зависимость огибающей абриса ВП; интерполяция по параболической гипотезе оказалась неэффективной.

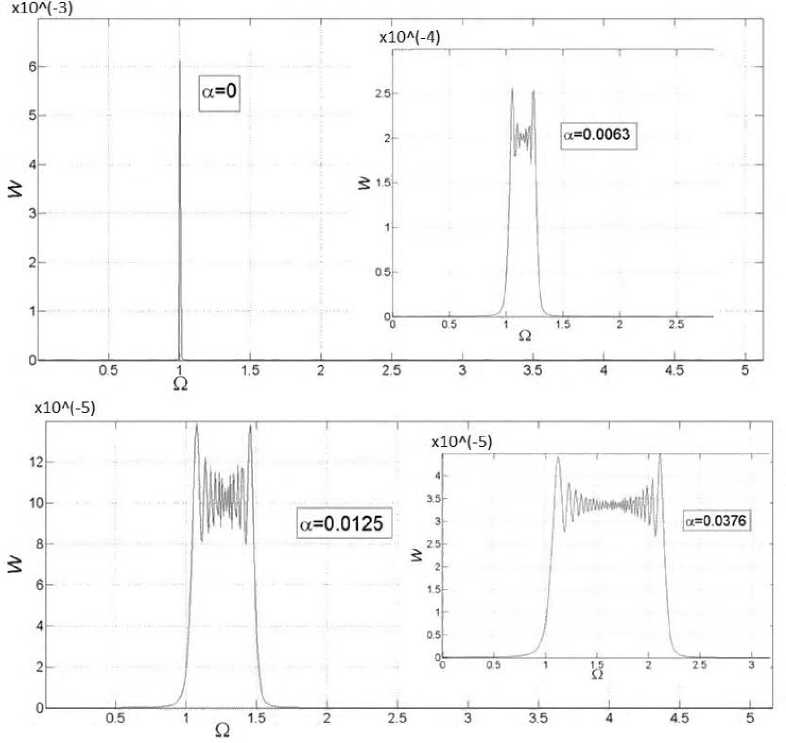
Рис. 1. Зависимость спектральной плотности W от частоты П для уравнения (5). Линеаризованный случай

Отметим превосходное совпадение частотных кривых, полученных по предложенной методике и непосредственно из уравнения (5). С помощью MATLAB Curve Fitting Toolbox интерполировали зависимость амплитуды от коэффициента нестационарности при сле- где m =    = 0.1591 (0.1591^0.1592), n = 0.25

2 п

дующей гипотезе: P ( а ) = m (1 + aN ) ⁿ

(0.2499÷0.2500). В скобках указаны доверительные интервалы для стандартного уровня ошибки 95. Такой результат является косвенным аргументом в пользу корректности пред- ложенной нами методики экстракции параметров (см. п. 1), поскольку аналитическое решение задачи известно. В [2] была получена обратнопропорциональная зависимость квадрата амплитуды P ЭМВ от частоты П при различных видах нестационарности, что и подтвер- ждают рис. 2 и приведенная выше степенная зависимость. Действительно, если предположить, что номинальная частота в (5) приблизительно равна производной фазы по времени, то

P(t)2dt (tП(t)) ~ P(t)2П(t) = const, const          const           1

откуда искомое соотношение: P = —,            = —^=(1 + aN ) 4 .

-4/(2 п ) ² (1 + aN )    V^ ^V ’

Соотношение (6) выполняется точно для мгновенных величин и приближенно для дискретных отсчетов, получаемых при «концевом» анализе.

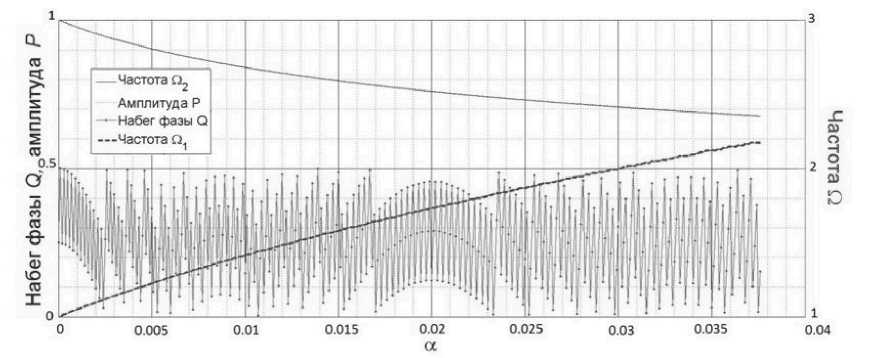
Рис. 2. Зависимость экстрагированных из решения (5) набега фазы Q , амплитуды П 1 (все в конечной точке) от параметра нестационарности. Построена кривая для частоты П ₂ = V1 + aN в конечной точке ( N = 100). Амплитуда волны нормирована фазы нормировался на 2 п

P и частоты номинальной

на — • Набег

На абрисе набега фазы наблюдаем феномен арки, когда набег фазы не достигает своих крайних значений, а огибающая имеет форму арки. Такое встречается дважды: при совсем малых a < 2 • 10~4 и на отрезке a = 0.02 ± 0.015. Инженерный смысл явления «ар- ки», по-видимому, состоит в том, что именно в этих диапазонах нестационарности следует проводить измерения по деградации среды или налагать информационную составляющую сигнала в фотонных приборах.

5.    Исследование линейной модели нестационарности

В случае линейной нестационарности имеем для T 1 j (для T 0 аналогично с перестановкой a и b , индексы для простоты писать не будем, t размерно):

е ( t ) = е (0)(1 + at ) , ^ ( t ) = ^ (0)(1 + bt ) ,

_ T ⁽ t ' ' ( (1 + at )(1 + bt ) ⁺ 4(1 + at ) ² ) T ⁽ t ) = ⁰

При a = b дифференциальное уравнение имеет аналитическое решение вида ~ cos(ln t ). Хотя вывод для общего случая приводился в первой части статьи, уместно привести более простой вывод для данной ситуации.

2 + a¹²

Будем искать решение уравнения T" ( t ) +         T ( t ) = 0 как (1 + at ) ^Л , что даст нам

(1 + at ) ²

квадратичное условие на А , причем корни будут мнимые с Re Л = ^:

а ² - ^{л +} (_а2⁺ 4^ =⁰ , ^{Л 1} , ² = 2 ^±;?.                      (8)

aa

Суперпозиция двух комплекснозначных решений даст нам общее вещественное решение:

T ( t ) = CV 1 + at cos ( ln(1 + at ) + D ) .

Здесь C, D - константы, которые можно найти из граничных условий при t = 0. В пределе а ^ 0 (9) естественным образом переходит в закон косинуса. Следует отметить, что даже в предположении ш ^ a, at ^ 1 набег фазы в (9) может быть существенным на высоких частотах, что вполне соответствует выводу в [2]. Этот набег, если разложить логарифм в ряд, приблизительно равен ( t^wa ) ² . Здесь набег фазы отсчитывается от момента t = 0.

При a = b точного аналитического решения (7) найти не удается, но можно заменить уравнение приближенным:

T" ( t ) +

ω ²

(1 + at )(1 + bt )

T ( t ) = 0 .

При b = —a решение (7) вида (9) возможно, как показывает анализ (10), лишь при ш ² = 2 a ² , что выводит за пределы исходного предположения ш ^ a , и формально записывается как T ( t ) = 1 — a ² t ² .

Для численного исследования перепишем уравнение (7) в безразмерных величинах:

д ² T          2 п ²             a ²                      2 na     2 nb

+ ( 7------ +              T ( t ) = 0 , a =---, в ⁼---*

dt ²      (1 + at )(1 + et)   4(1 + at ) ²                    ш ш

Предположим, что a = в .

В отличие от линеаризованного случая ВП локализуется слева от единичной частоты, что и следует из уравнения (11), амплитуда наиболее выраженной гармоники при малых α падает медленнее, чем в линеаризованном случае, и растет при больших α . Появляющиеся на абрисе биения асимметричны (сдвинутые влево гармоники ВП вносят больший вклад, чем сдвинутые вправо), при больших значениях α сглаживаются. При возрастании α ширина пика уменьшается, однако появляется хвост ВП. При росте α огибающая пика приближается к оси абсцисс, появляется хвост. При экстремально больших значениях a ^ 1 мы получаем единичный пик при частоте, близкой к нулю, что можно трактовать как трансформацию ВП в одну инфракрасную моду. Видность растет (рис. 2) с ростом α , а вот номинальная ширина ВП меняется незначительно и противонаправленно.

Кривые двух частот Q i и Q 2 совпадают. Кривые P ( a ) , Q 2 ( a ) коррелируют друг с другом, а именно соблюдается обратная зависимость квадрата амплитуды и частоты. Так же, как и в линеаризованном случае, при небольших значениях α набег колебания набега фазы происходят чаще. Арка в данном случае появляется при меньших значениях α , также можно увидеть еще одну слабовыраженную арку. Вогнуты арки в противоположную сторону (по сравнению с линеаризованным случаем). Обращает на себя внимание эффект обращения (зубцов) на кривой Q ( a ) в области больших a , когда происходит быстрый набор фазы и более медленное его падение. При этом плотность зубцов падает. Также отметим эффект дрожания амплитуды, видимый на рис. 4 на правом конце кривой P ( a ), - его мы связываем особенностями метода экстракции, не исключая фактора приближенного выполнения (6).

„        1 Г? a ² V

На рис. 3 построена кривая для номинальной частоты Q 2 = (1 + —N- ( 4(2 ) 2 + 11

в конечной точке N = 100. Амплитуда волны нормирована на —. Набег фазы в начальной точке, как и ожидается, равен п/ 2 и нормировался для удобства на 2 п .

Обсудим линейный случай при в = -a .

Рассматривались значения a <  0 * 01, так как при остальных исходное уравнение не имеет смысла (проницаемость принимает отрицательные значения). Амплитуда наибольшей гармоники монотонно падает с ростом α (в отличие от синфазного изменения проницае-мостей). ВП локализуется справа от единицы. По сравнению со случаем a = в количе-ство/плотность биений заметно меньше, в остальном абрис тот же – хвост по-прежнему сохраняется. В отличие от предыдущего случая ширина пика и видность растут при увеличении α , причем видность при максимальном значении близка к 1.

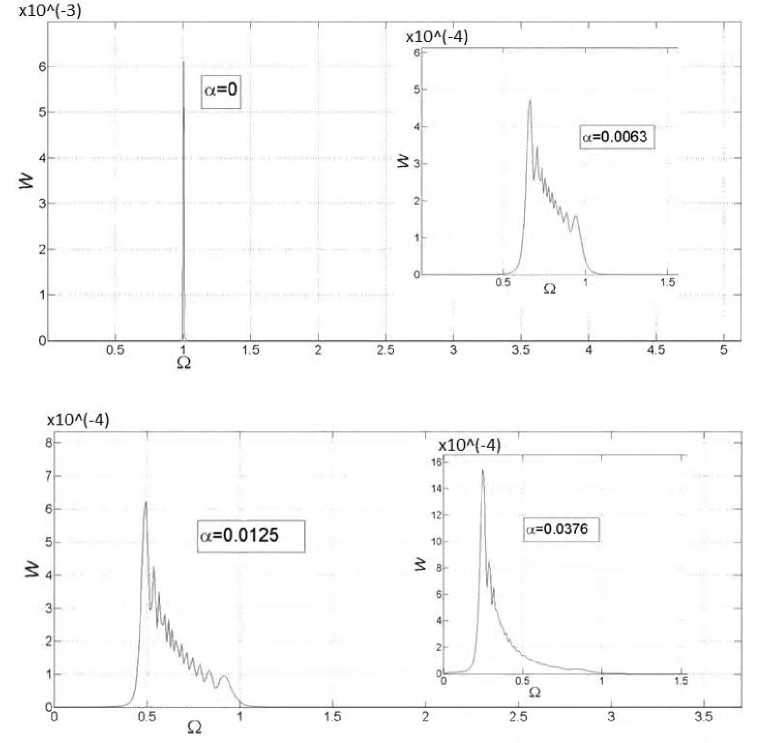
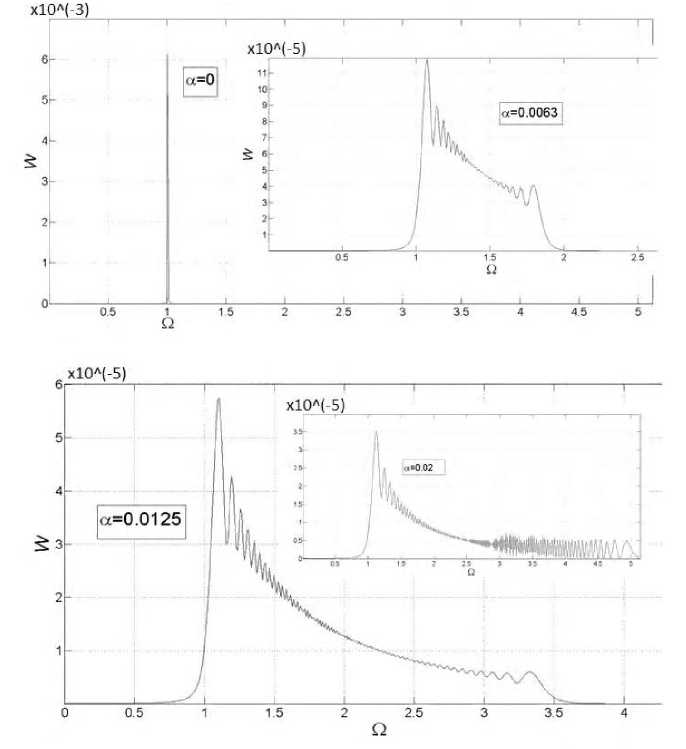
Рис. 3. Зависимость спектральной плотности W от частоты П для уравнения (11). Линейный случай при а = в >  0

Что касается «концевого» анализа, то амплитуда падает, вначале медленно и затем более круто (при а >  0 . 01). Так же, как и при синфазном управлении, наблюдается начальная полуарка на графике набега фаз. Вторая арка довольно узкая и относится к форме абриса, не являясь огибающей, как в синфазном случае. Почти сразу за ней идет последняя, третья и весьма глубокая, т.к. падает почти до нуля, арка.

6.    Экспоненциальная модель нестационарности

е ( t ) = е (0) exp( —at ) , ^ ( t ) = ^ (0) exp( —bt ) ,

T" ( t ) + ^ 2 2 exp( a + b ) t —4^ T ( t ) = 0 .

Считаем a = b , и тогда в прежних обозначениях имеем:

∂ ² T

_ ~о—+

^ (2 п ) ² exp 2 at —

α ²

т) T ⁽ t )

Амплитуда максимального пика довольно быстро падает вследствие расширения ВП, локализованного справа от единицы (что подтверждается и центроидом, см. табл. 1). До некоторого значения частоты гармоники амплитуда биений падает (при увеличении их плотности), а после, наоборот, растет при уменьшении их плотности вплоть до последнего «росчерка». Видность и ширина ВП умеренно растут с увеличением α .

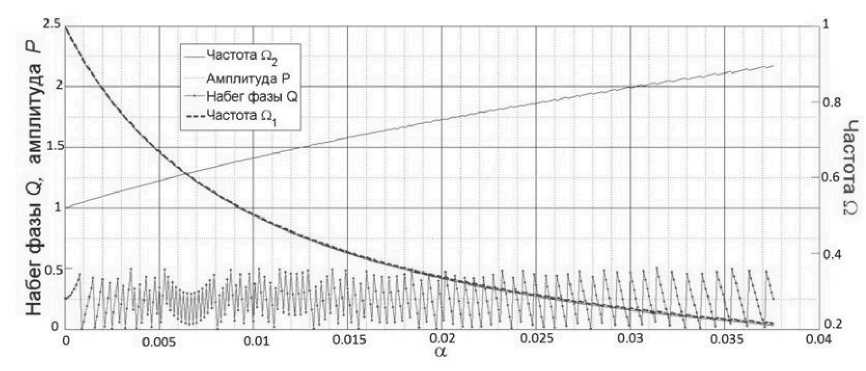
Рис. 4. Зависимость экстрагированных из решения (11) набега фазы Q , амплитуды P и частоты Ω 1 (в конечной точке) от параметра нестационарности

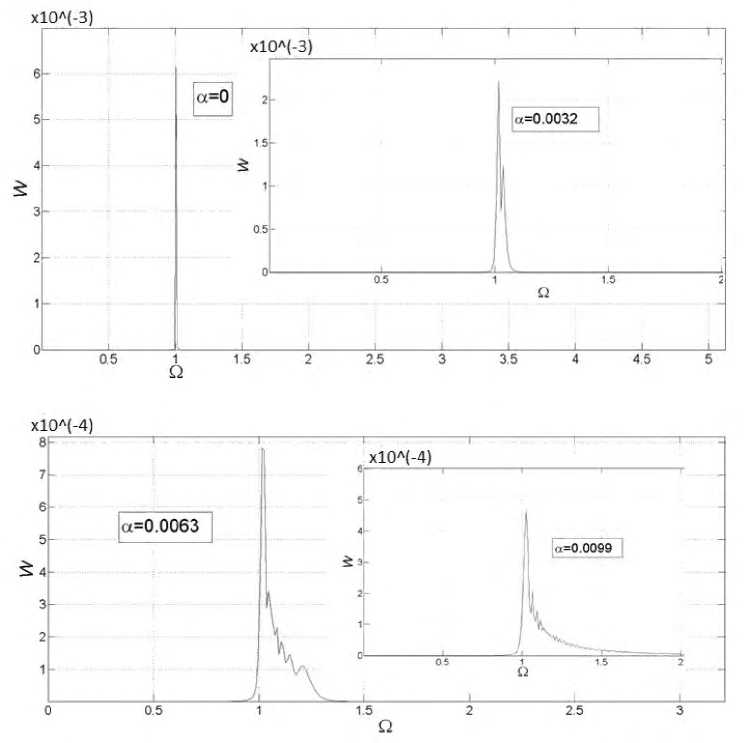
Рис. 5. Зависимость спектральной плотности W от частоты Ω для уравнения (11). Линейный случай при β = -α

С учетом сделанного выше замечания формально при коэффициенте нестационарности, близком к а >  0 . 02, начинаются биения спектральной плотности с элементами хаоса. Это отличает случай от других, так как некоторые высокочастотные гармоники могут быть «выключены» из имеющегося спектра.

При «концевом» анализе (рис. 7), аналогично предыдущим случаям, кривые частот совпадают. Арки появляются чаще (их 3, не считая начальной), выражены наиболее четко, т.к. в отличие от предшествующего, что принципиально, уже не являются огибающими линиями. Наиболее ясно выражена арка с минимумом α =1 /N . Поведение набега фазы обнаруживает черты самоподобия (фрактальности) в «межарочных» интервалах; нахождение здесь теоретических зависимостей представляет собой интересную задачу для дальнейших исследований. А с точки зрения практики наличие особых диапазонов значения коэффициента нестационарности, где набег фазы изменяется медленно, интересен возможностью кодирования информации.

спектральной

Экспоненциальный случай при α = β

Рис. 6. Зависимость плотности W от частоты Ω для уравнения (13).

α ²

Построена кривая для номинальной частоты Ω2 =   exp(2αN) - 4(2π)2 . Амплитуда волны нормирована на . Набег фазы нормировался на 2π.

Также был исследован случай b = -2a. Центроид при этом сдвигался влево от единицы более медленно, ср. с рис. 6. Ширина ВП была меньше, чем при синфазном управлении. Существует такая же точка перегиба, но она менее выражена, правый край так же закан- чивается резким «росчерком».

Обратим внимание, что существует α = α∗ ≈ 0.09723 (по-прежнему β = -2α ), см. (12) и (13), при котором номинальная частота обращается в ноль на конце интервала. «Концевой» анализ показывает небольшое расхождение частот, т.е. Ω1 =Ω2 → Ω1 ≈ Ω2, более заметное при больших α; визуально частота падает линейно, хотя реализуется приближенно экспоненциальный закон (квадратичным слагаемым в (13) можно пренебречь) в области малых аргументов. Феномен арки возвращается к абрису огибающей; первая полуарка приходится на начальный участок а < 0.002, при этом набег фазы (нормированный) меняется от стартовых 0.25 до почти максимального уровня в 0.5, а вторая наблюдается в промежутке α ≈ 0.011÷0.014. Эти диапазоны не слишком сильно отличаются от предыдущего случая, то уже третья арка не наблюдается. Плотность зубцов падает при увеличении α.

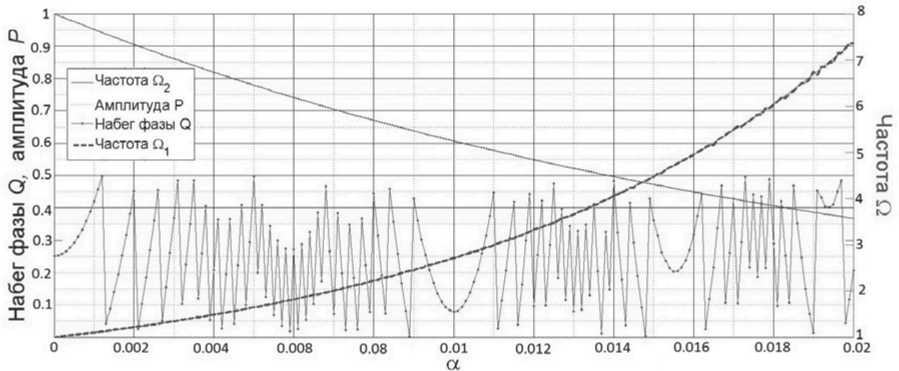
Рис. 7. Зависимость экстрагированных из решения (13) набега фазы Q , амплитуды P и частоты

П 1 (в конечной точке) от параметра нестационарности

«Концевой» анализ проводился также для следующего участка 0 . 02 < а С 0 . 064 < а * ~ 0 . 097. Амплитуда зубцов на кривой набега фазы становится все большей, временами превышая 0.5; одновременно с этим усиливается эффект дрожания кривой P ( а ). Однако эти особенности получены в той области, где методика уже не вполне ««работает», где кривая T ( t ) лишается «синусоидального» характера. Однако в этой области действителен фурье-анализ; типичный абрис состоит из резкого пика при Q ~ 0 (+0 . 1) и небольшого хвоста справа, где практически незаметны биения.

Аналогично линеаризованному случаю интерполировалась зависимость амплитуды вол- ны от коэффициента нестационарности. Для случая a = b получили P(а) = exp(11а), где 11 = —50, (—50.01, — 50), то есть результаты имеют высокую точность. Вместе с тем для a = — 2b P(а) = exp( 12а), где 12 = 24.82(24.79, 24.84). Результаты также соответ- ствуют полученной обратнопропорциональной зависимости квадрата амплитуды волны от

частоты. Если в формуле для частоты

У exp(( а + в ) t) —

α ²

4(2 п ) ²

пренебречь вторым слагае-

мым по сравнению с экспоненциальным, то получим следующую формулу для амплитуды:

P ( а, в ) = exp

(4е")

, что удовлетворяет

7.    Гармоническая модель нестационарности

Существует два пути внесения гармонических нестационарностей при разных соотношениях уже пары, а не одного, коэффициентов нестационарности a, b, что делает анализ многовариантным. Рассматриваем сразу безразмерные уравнения (14) – (18), (20) с α ≡ π , β ≡ π , γ ≡ πp, где p << ω, и берем за основу пару < γ, α/γ >, где γ – ωωω α частота модуляции проницаемостей, и — < 1 - амплитудный коэффициент, который пока-γ зывает, насколько меняется диэлектрическая проницаемость (в относительных единицах). Для наглядности в уравнениях вынесем (2п)2 - так мы удостоверимся, что при нулевых коэффициентах нестационарности действительно получается уравнение для невозмущен- ной волны. Таким образом, решаемое уравнение имеет вид

+ ((2 ^{п ) 2} + q ^{( —}, t)) T ⁽ t) = 0. dt ²

Напомним условие обезразмеривания е ( t = 0) = ц ( t = 0) = 1.

7.1.    Синусоидальное управление, α = β £(t) = £(0) (1 + a sin(pt)) , Ц(t) = Ц(0) ( 1 +— sin p (Pt)} а^а,Ь^в,Р^Ү,а=в ^ q(a,t) = —2 - (pn )2 - 22) (2s+s2) (1 + s )2 s = — sin( Yt). Рис. 8. Зависимость спектральной плотности W от частоты П для уравнения (14). Гармонический случай (5.1) при — = в

При повышении частоты возбуждения γ абрис ВП приобретает игольчатый вид, а в дальнейшем спектр ВП из непрерывного становится дискретным, что коренным образом отличает гармонический случай от предыдущих и затрудняет применение методики анализа фурье-спектра. На рис. 8б рядом с основной гармоникой появляется малоамплитудная, причем они практически симметричные. Например, при ү = 1 наблюдается 7 гармоник и несколько малоамплитудных. Причем наиболее выраженная гармоника находится вблизи 1. Узость пиков сравнима с величиной численной ошибки по оси частот.

Физического смысла это не имеет, однако рассматриваем значение ү = 4п, так как при этом в (14) уйдут несколько членов, а при значениях — ^ 0 получится случай невозму-γ щенной волны, что показывает рис. 8. С учетом (14) верна формула (15), показывающая существование пар коэффициентов нестационарности, дающих нам гармоническое решение:

^ 2 Т         а ² - ү ² +4(2 п ) ² X

дР ⁺ V 4 ⁺    4(1 + s ) ²     ) ⁽ t )   0 ’

А именно, при а2 — ү2 + 4(2п)2 = 0 гармонический сигнал имеет частоту ү/2, что соответствует выводам в [2]. В частности, сигнал сохраняется невозмущенным тогда и только тогда, когда гармоническая нестационарность имеет нулевую амплитуду. Мы не можем снизить частоту исходной ЭМВ, но можем её увеличить, например, в 1.5 раза с помощью высокоамплитудного (а/ү = 5/3/3) возмущения; подобную ситуацию демонстрирует рис. 8в. Вместе с тем мы можем получить (рис. 8б) суперпозицию гармоник: на основную моду, имеющую частоту, большую частоты исходной ЭМВ, накладывается малоамплитуд- ная гармоника, сдвинутая к меньшим частотам.

«Концевой» анализ проведем по двум параметрам только для амплитуды P ( ү,а/ү ). Общая картина для прямоугольника { ( ү,а/ү ) } = (0; 2 п ) х (0; 1) неоднозначна, сеточная функция задана на слишком крупном шаге – 0.1 по первому и 0.01 по второму аргументу (а меньший шаг естественно требует ресурсоемкости). Тем не менее можно сделать ряд замечаний:

• •    нормализованная на начальную амплитуду, т.е. P/P ( t = 0) ,P ( t = 0) = 1 / (2 п ), изменяется в пределах ~ 0.24+1.38;

• •    вплоть до ү ~ 4 . 5 вертикальная структура контурного графика повторяется, при этом P сильно зависит от ү , но слабо от значения а/ү ; при ү >  6 линейчатая структура разрушается, появляются островки, причем крупные характерны для нижней половины и

• выгнуты вправо;

• •    период по аргументу ү составляет примерно 0.4.

Начальный фрагмент показан на рис. 11, где видна периодичность.

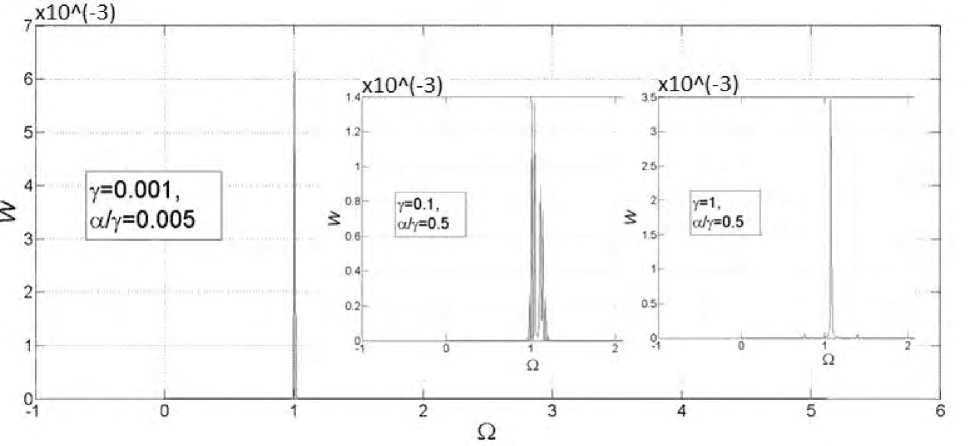
Рис. 9. Фурье-образ решения (15) при некоторых парах ( α/γ , γ )

Можно фиксировать один из параметров, например γ, и проводить «концевой» анализ по обычной схеме. Для ү = 0.01 примечательно, что амплитуда монотонно растет (и частота соответственно уменьшается), хотя гармоничность нестационарности среды не предполагает изначально направления изменения амплитуды; на кривой набега фазы феномен арки отсутствует. Однако более интересен случай ү = 0.5 ^ 2п, см. рис. 10. Во-первых, изменилось направление изменения амплитуды; во-вторых, на кривых амплитуды и частоты становятся заметны «дрожания», более сильные в конце, т.е. при 0.5 < а/ү < 0.95, плот- ность которых возрастает; в-третьих, на заключительном отрезке мы наблюдаем феномен арки (здесь наиболее выделены три арки, одна – по огибающей, две других – по самой кривой), но этот эффект отсутствует на кривой набега фазы. Теперь пусть γ = 0.4. Что изменилось? Феномен арки стал наблюдаться и на кривой набега фазы, причем одновременно с двумя другими кривыми (амплитуды и частоты). «Дрожания» стали менее выраженными. Концевая амплитуда вновь стала возрастать, а не падать; её поведение сложное – так, в ситуации аналогичной рис. 10, мы наблюдаем рост амплитуды при γ = 0.01, 1.1 и её падение при γ = 0.1, 0.6, 1.5. При γ ∼ π и выше методика перестает работать, т.к. нормированный набег фазы превышает 0.5.

Наличие арок на последних кривых (рис. 10) заставляет подробнее рассмотреть точки ( γ, α/γ ) = (0 . 4 , ≈ 0 . 75) ∪ (0 . 4 , ≈ 0 . 83), приходящиеся примерно на центры арок. Обратим внимание, что ранее совпадавшие кривые номинальной (Ω 1 ) и экстрагированной (Ω 2 ) частот начали расходиться, что объясняется «включением» слагаемого t Q ' в приближенной формуле (6).

Как показывает рис. 11, понятие «амплитудная модуляция» является хорошим представлением для анализа.

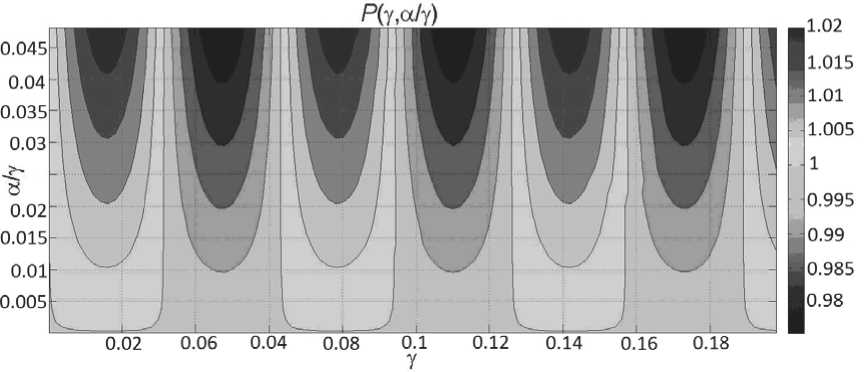
Рис. 10. Контурный график амплитуды в области малых значений аргументов. Амплитуда нормализована на 1 / (2 π ). Пределы и шаг (в скобках) изменения по аргументам: γ→ 0 . 0001 : (0 . 002) : 0 . 2 ,α/γ → 0 . 0001 : (0 . 002) : 0 . 05

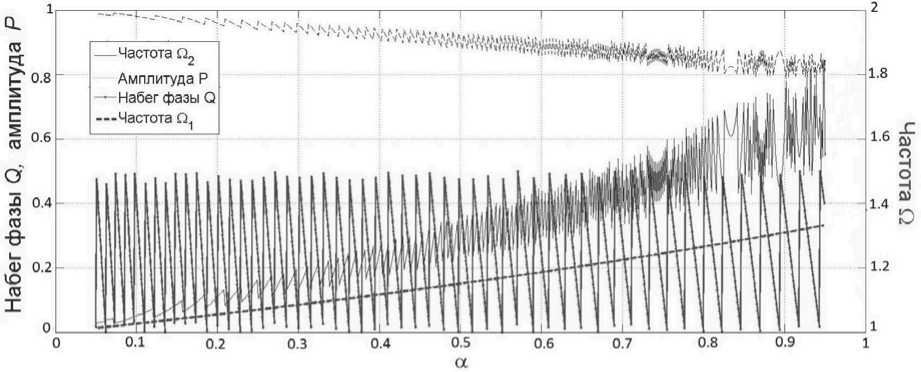
Рис. 11. «Концевой» анализ для синфазного гармонического управления. Случай

γ =0 . 5 ,α/γ =0 . 05 : 0 . 001 : 0 . 95. Обозначения рис. 7

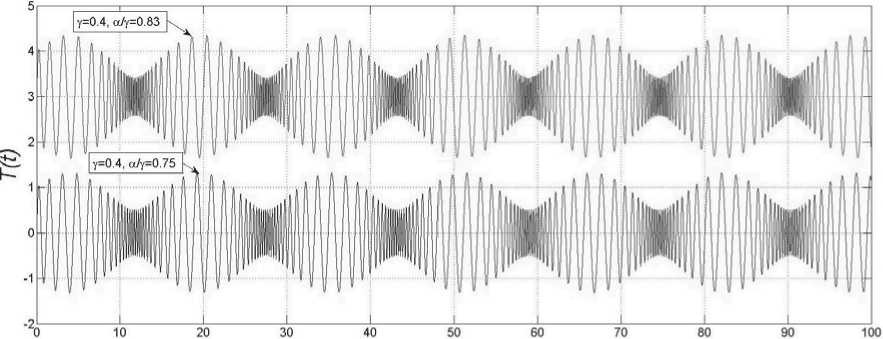
t

Рис. 12. Графики решения (14) в точках ( ү, а/ү ) = (0 . 4 , re 0 . 75) U (0 . 4 , re 0 . 83). Для удобства: знак тильды у аргумента не ставим, обе кривые нормированы на 1 / 2 п , вторая кривая сдвинута вверх на +3

7.2.    Синусоидальное управление, β = -α Е(t) = Е(0) (1 + p Sin(pt)) , Ц(t) = Ц(0) (1 + Р Sin(pt)) a→α,b→β,p→γ,α=-β ^ d2 T   / ү 2   (4(2 п )2 + а а dtp + V + - ү2) + (4(2n)2 4(1 + s)2(1 - s) " а 2 + ү 2) s ) T (t) = 0.

В этом случае не существуют значений коэффициентов нестационарности, дающих гармоническое решение, так как на всем отрезке числителя (16) нулю равняться не может. Тем не менее, как мы увидим дальше, решение может быть весьма похожим на гармоническое.

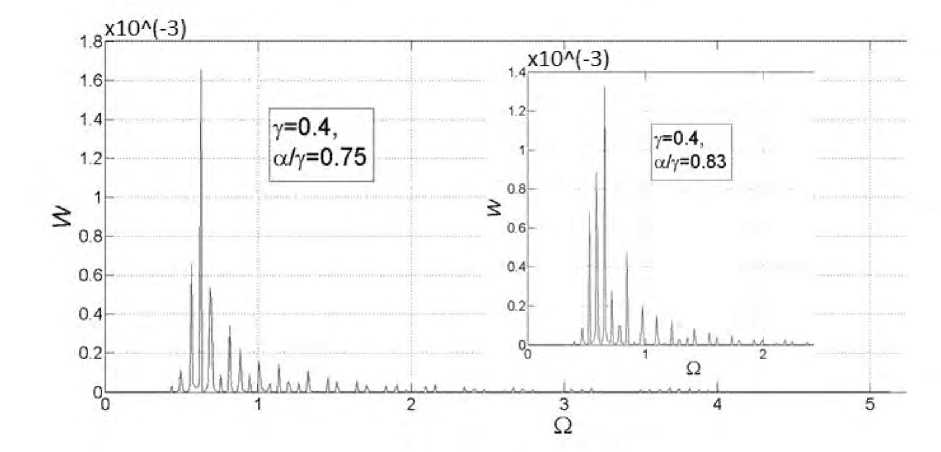
Рис. 13. Зависимость спектральной плотности W от частоты П для уравнения (16). Синусоидальная нестационарность при а = —в , т.е. противофазном управлении

В отличие от синфазного управления, исключая ситуации больших значений параметров (рис. 14) дискретности спектра, ВП не наблюдается, сам ВП компактен и имеет небольшую ширину. Даже при относительно значимых по величине параметрах нестационарно-сти имеется один узкий пик, ширина которого близка к вычислительной ошибке (рис. 8).

Так, в предположениях рис. 9, но уже для противофазного управления, изменения амплитуды в пределах 4-го знака после запятой (причем всегда в отрицательную сторону). Требуется ү ^ 1 ,а/ү ~ 0 . 1 , чтобы \P/P ( t = 0) — 1 | ~ 0 . 0035. «Концевой» анализ показывает незначительность отклонений амплитуд от частот (по сравнению с 5.1), а феномен арки начинает проявляться при поздних значениях а/ү >  0 . 9. Кроме того, если в синфазном случае амплитуда изменяется практически линейно, то в противофазном случае амплитуда падает по выпуклой кривой. Небольшие значения γ гарантируют незначительность «дрожаний» на кривых амплитуды и частоты, но не гарантируют малого разброса значений P, Q( ү = const ,а/ү ): так, при ү = 0 . 01 на отрезке а/ү Е [0 . 05; 0 . 95] нормированное значение P падает примерно на 0.22, а при ү = 0 . 5 такое изменение составляет 0.03.

На рис. 14. показана ситуация достаточно сильной нестационарности, когда его частота составляет половину исходной частоты и амплитуда равна половине от исходной проницаемости среды.

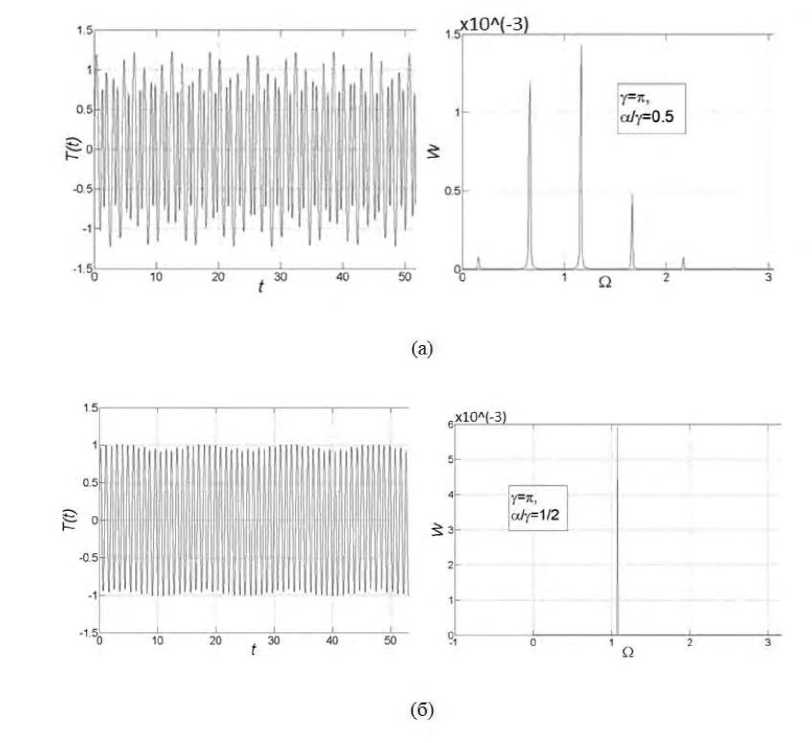
Рис. 14. Сравнение результатов синфазного (а) и противофазного (б) управления в точке ( ү = п,а/ү = 1 / 2). На левой стороне показан график решения T ( t ) (для удобства ограничен 50, а не 100), на правой – его фурье-разложение

7.3.    Косинусоидальное управление

В рамках косинусоидального управления также можно выделить синфазный (17) – (18) и противофазный (20) случаи:

E ( t ) = E (0) f1 + a (1 ^p

-

^cos( pt ))) , ц ⁽ t ) = ц (0) (1 ⁺ p ⁽¹

-

) а^а,Ь^в,Р^Ү,а = в ^

q ^{( a,}t ) =

7 ²

- (2 n ) ² a (2 + a ) + (,2 n ) ² - 7)(

1 + ^а

-

(a + -)²

a (з + “ ) + a ²)

A , a = 1 - ^a cos( ^..

Основное уравнение (2) с учетом подстановки (17) можно переписать в более удобной форме (18):

^d 2 ^{T           4(2 n ) 2 - 2} «₇ ^- 7 ² \

dt ^{2 +} V 4 ⁺    4( a + a/₇ ) ²    ) T ⁽ t )   ⁰ '

Рассуждая аналогично (15), получаем условие гармоничности решения:

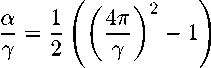
о 7 = л/a ² + (4 n ) ² - a, 7 = 4 п о ш.

Из (18) и (19) следует, что точке минимума соответствует граница области, т.е. a/ү = m ~ 1. Если отбросить требование строгой гармоничности и принять слабую зависимость от времени знаменателя (18), то становится понятным такой численный результат - при ( 7,0/7 ) = (6 п, 3 / 4) спектр содержит единственный узкий пик на частоте 0 . 35.

Противофазное косинусоидальное управление приводит к (20):

а^а,Ь^в,Р^Ү,а = в ^

E ( t ) = E (0) ( 1 + a (1 - cos( pt )) ) , ц ( t ) = ц (0) ( 1 + -(1 - cos( pt )) pp

(— d ² T ч ² U dt ^{2 +} 4 ⁺

2 j^j^(2 ^п 7(l ⁺ ; ү Д -(a^ү +j|₁(2 _: 7) ^— 7^' f 1 + ^a (1 - cos( 7 t))^ f 1 - ^a (1 - cos( 7 t))^

T ( t ) = 0 .

V 7          V V   7          )         /

Аналитическое исследование затруднено громоздкостью выражений, а численного ис- следования мы не проводили.

7.4.    Сравнение синфазного и противофазного управления: концевая амплитуда

Остановимся на частном вопросе объяснения, исходя из вида (15) и (16) и представления уравнения Штурма–Лиувилля, почему в синфазном случае концевая амплитуда P ( a ) = P ( 7 = const ,—/y ) ^= n может как убывать, так и возрастать ( dP/da ><  0), а в противофазном – только убывать?

Приведем несколько соображений. Заметим вначале, что, считая вполне верным (6), для относительного изменения амплитуды δ можно записать линейное разложение (21):

P ( -,t = N )

P ( •J =0)

- 1=

I     2П у 2п + q(a,N)

- 1

q ( a,N ) 4 п

Далее, если индексом 1 отметить синфазный, а индексом 2 – противофазный случаи,

получим (22):

^{2(2 п ) 2} s        _«

^q 1 ^- q ² = ^- (! + s ) 2 ₍₁ - s ) • ^s = ү =™< ^YN ) .

Сделав подстановку (22) в (21), получим независимость от α знака разности концевых амплитуд. С другой стороны, этот знак зависит от выбора концевой точки N и частоты возбуждения, что как будто снижает ценность этих замечаний. Однако надо учесть, что 5 ( a ) относится к дискретным отсчетам амплитуды P , которая экстрагируется по определенной схеме, а не амплитуды P , с которыми связано (22) и которые берутся из непрерывного соотношения (6). Поэтому если рассуждать для концевых значений, когда в течение полупериода ∼ π/γ они не изменяются, то целесообразно усреднить (22). Тогда получим эллиптические интегралы (23), (24):

^{2 П}Һ    -      - -        „ Г ¹    V l - ^2

α

> 0 . g = -^γ

1 - q 2 > = ТТ      ( q 1 ( t) - q 2 ( t))dt = 16 ng ^{2       V}₂ z dz

2 п/ү о                               о (1 - g ² + g ² z ² ) ²

В тех же обозначениях среднее значение q 1 зависит от обоих параметров:

< q i ( t) >  = - г +

a ² + 4Г 2 П

(1 + g ² z ² ) dz

(1 — g ² z ² ) ² V 1 — z ²

Мы видим, что знак 1 >  (24) не определен, а знак 1 - q 2 >  положителен. Если абсолютное значение первой величины меньше второй, тогда становится ясным поведение концевой амплитуды в противофазном случае.

Можно посмотреть на уравнение Штурма–Лиувилля как на возмущенное поправкой

q(-.N) уравнение гармонического осциллятора, где частота 2п играет роль собственного значения оператора. Тогда попытаемся применить методы теории возмущений [9], ограни-

(УК ^-)

чившись членами второго порядка по параметру

< 1. Формальная техника

диктует искать асимптотическое решение в виде (25):

т ( t )= т о ( t ) + - ^γ

т 1(У + ( !)² T 2(0 , T о(0 ^ ^sin(2

2 п

, т 1 (0) = T 1 (о) = т 2 (0) = T 2 (о) = о .

Также предположим второй порядок в разложении возмущения. Введя два коэффициента, выпишем (26):

q ( ^- ) = q ⁽¹⁾ ( i.t)^{- +} q ⁽²⁾ ( -M) ( ^- ) .

Тогда, подставляя (25) в (14) и учитывая (26), приравняем к нулю коэффициенты разложения при первой и второй степени и получим условия для нахождения T i , 2 ( t ) из дифференциальных уравнений (27):

T 1 ' + (2 п ) ² T 1 = -q ⁽¹⁾ T о .Т ! ^ + (2 п ) ² T 2 = -q ⁽²⁾ T о - q ⁽¹⁾ T i .               (27)

Поскольку в правых частях неоднородных уравнений (24) стоят произведения синусов, то решением (27) будут сумма гармоник с некоторыми весовыми коэффициентами, а именно такая картина и наблюдается на рис. 12, 14. Эти веса могут быть выведены аналитически. Наибольший из них вес (и соответственно выделяющий основную моду), по-видимому, можно интерпретировать как концевую амплитуду.

Для синфазного случая, учтя (14), выпишем коэффициенты:

q ⁽¹⁾ = - 2rsin( -t) ,q ⁽²⁾ = 2 (зГ+ - 2)

зг                         - ‘²

^- у cos⁽² -t ) . ^г = ^{(2 п ) 2 -} —.

Для противофазного случая, учтя (15), также выпишем коэффициенты:

q ⁽¹⁾ = у sin Yt), q ⁽²⁾ = 2^r - 2 (^r - ^ co^s(2 Yt).

В синфазном случае из (25), (27), (28) следует выражение для T i :

cos(2 п — ү ) t + cos(2 п + ү ) t 4 п — ү       4 п + ү

T 1 =

cos(2 πt )

γ

+^Γ 2 πγ

.

Отметим, что, несмотря на видимое наличие в знаменателе (31) ү , lim _ү > о T i ( ү ) = 0, и это отвечает физическому смыслу. В правой части неоднородного дифференциального уравнения для T 2 находятся 5 мод со следующими весовыми коэффициентами:

T” + (2 п ) ² T 2 = У A y sin ( (2 п + гү ) t) ,  A о = — 2 п, A ± 2 = ± ^Г(2 ^{? ± ү} ) , A ± 1 = Т ^Г . (31)

r = - 2                                         ^{4 пү            ү}

В общем виде результат согласуется с экспериментом (рис. 7, 8, 13, 14). К сожалению, решение (31) будет всегда содержать, т.к. A о = 0, растущее во времени резонансное слагаемое. Это говорит о том, данный асимптотический метод, даже если повысить порядок разложения, не совсем применим в нашем случае. Возможно, для лучшего анализа целесообразнее было бы применять метод усреднения Крылова–Боголюбова (формула (23) идейно с ним связана), а не разложение по малому параметру (25).

8.    Заключение

Мы проанализировали несколько случаев управления ЭМВ через внесение нестацио-нарности в среду распространения. Полученные нами результаты, к сожалению, не имеют прозрачного физико-технического смысла. Эмпирические результаты численного эксперимента на основании гармонического «концевого» анализа уравнения Штурма–Лиувилля, если суммировать наиболее важные из них, состоят в следующем:

• •    при гармоническом управлении спектр ВП обычно дискретный, что отличает этот случай от других;

• •    наблюдаются от 1 до 3-4 дискретных диапазонов изменения параметра нестационар-ности, когда набег фазы для концевой точки изменяется медленно; в этих диапазонах либо огибающая абриса, либо сама кривая набега фазы имеет форму арки;

• •    косинусоидальное управление, на наш взгляд, более перспективно с точки зрения практики, т.к. позволяет не только увеличивать исходную частоту ЭМВ, но и уменьшать её (но не более чем в V2m + 1 ~ V3 раз, считая, что технически проницаемость изменяема не больше чем в 2m + 1 ~ 3 раза); уменьшения частоты можно достичь и на большую величину, но лишь допустив небольшое уширение моды;

• •    направление перекачки энергии ЭМВ при гармоническом управлении: в синфазном случае определяется только частотой управления, а в противофазном случае – амплитуда волны падает (а частота возрастает).

9.    Приложение

Эффект арки, найденный нами впервые, представляется полезным для использования на практике, например, для информационной модуляции ЭМВ в волноводе. Происхождение эффекта арки и черты фрактальной геометрии на некоторых кривых набега фазы требуют дополнительного теоретического исследования.

1; Mt=1e+5; N=100; M=1024; Fs=Mt/N; d=1e-5; h=0.001;

2; options = odeset(’RelTol’,d,’AbsTol’,[d d]);

3; [t,T] = ode45(@maxwell,0:h:N,[0;1],options);

4; t1=linspace(0,N,M); t1=t1’; x=T(:,1); x1=interp1(t,x,t1,’spline’);

5; Y=fft(x1,M)/M; Y=Y.*conj(Y); W=fftshift(Y);

6; Omega=((t1-N/2)*Fs/N); plot(Omega,W);