Численное исследование процессов в суперкавитационном испарителе с учетом термодинамических эффектов

В условиях обострения дефицита пресной воды актуальность совершенствования существующих и разработки новых методов кондиционирования воды питьевого назначения не вызывает сомнений. Одним из перспективных способов обессоливания воды является применение суперкавитационных испарителей.

В отличие от известных методов процесс испарения в аппаратах суперкавитирующего типа осуществляется за счет создания развитого кавитационного течения при обтекании не-догретой жидкостью кавитатора с последующим отбором пара из образовавшихся каверн [1]. Здесь высокая интенсивность теплообмена по сравнению с другими способами генерирования пара объясняется особенностями процесса испарения с поверхности каверны. Например, если при теплоотдаче от стенки к кипящей в трубе жидкости паровые пузырьки образуются вследствие фазового перехода, требующего перегрева жидкости и повышения давления пара в пузырьке по отношению к давлению в окружающей жидкости, то при испарении жидкости в каверну наблюдается совершенно иная картина. В этом случае каверна образуется за счет гидродинамики потока – увеличения местных скоростей течения при обтекании кавитатора и, соответственно, уменьшения давления ниже давления насыщенных паров. Вследствие этого при суперкавитационном испарении возникает ряд дополнительных движущих сил и факторов, усиливающих испарение с поверхности каверны: разность температур, обусловленная

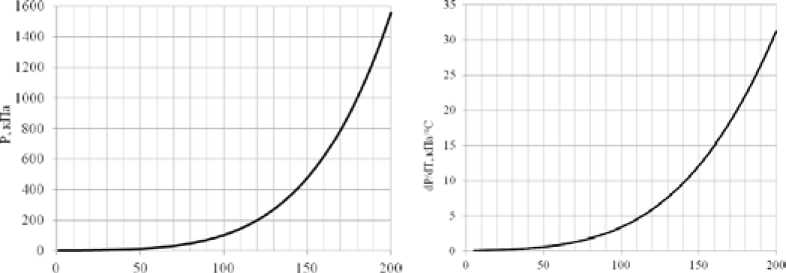
С увеличением температуры жидкости влияние тепломассообменных процессов на геометрические параметры кавитационных полостей становится существенным. При изменении температуры от 10 до 110 °С отношение плотности жидкости к плотности пара падает в 100 раз, что в сочетании с высоким значением теплоты парообразования оказывает существенное влияние температурного поля на кавитационное течение. Как видно из графиков, представленных на рис. 1, наклон касательной к линии насыщения водяного пара увеличивается [2].

Теплота парообразования, плотности жидкой и паровой фазы воды и давление связаны уравнением Клапейрона-Клаузиуса:

’P = L

В T T (V-V)"

Для изотермических случаев интенсивность кавитации при течении жидкостей определяется числом кавитации о_ю = ( P „ - P v ( Т _ю ) ) J^SpU ^ , которое включает в себя постоянное давление насыщения при заданной температуре жидкости P v ( T ^ ) . Для неизотермических случаев в число кавитации о = ( P „ -P v ( T ) ) [0,5 p U '; входит давление насыщения, выраженное в виде функции от локальной температуры P v ( T ) . Принимая функцию P v ( T ) в рассматриваемом интервале Δ T непрерывной и ограничиваясь двумя первыми членами ряда Тейлора, получим уравнение

ОО

— ^Л T ; Л T = T-T < 0. ^{5 T} -_г P U 2

Уравнение (2) определяет зависимость числа кавитации от температуры. Как видно из этого уравнения, местное понижение температуры приведет к увеличению числа кавитации и, следовательно, понизит кавитационную интенсивность [3].

Т.«С                                                  т.т а                                           б

Рис. 1. Зависимость давления насыщения водяного пара от температуры: а – кривая насыщения водяного пара; б – скорость изменения давления насыщения от температуры

Математическая модель суперкавитационного испарителя

Для моделирования рабочих процессов суперкавитационного испарителя использовалась модель двухфазного гомогенного потока. Эта модель основывается на предположении локального кинематического и термодинамического равновесия между фазами и не предполагает поверхность раздела между паром и водой. Здесь не учитывается выделение тепла за счет вязкостного трения, а принимается условие, что температурное поле определяется только испарением и конденсацией. Кавитационное течение жикости в этом случае описывается уравнениями неразрывности, сохранения момента импульса, уравнением сохранения энергии и уравнением переноса жидкой фазы, представленными в стационарном виде [3–7]:

W п

---------= 0, 8 х

^j _ 6P + дx        дxt дx j    ij

Apj h + f v L ) ] = 8 x

U + Pt )

д ui д uj +— дx -   дx

V j i

_

2 дUk § 3 дxk

d x j [( Pr m Pr_T J 8 x j

d ( a и )

-----— = m+ + m ~, 8х, где pm - плотность смеси; L - теплота парообразования; цm - коэффициент динамической вязкости смеси; P – давление; h – удельная энтальпия жидкости; Pr – число Прандтля.

Теплофизические параметры смеси фт и массовая доля пара f определяются выраже-m ниями

Ф m =« l Ф l +(1 -а l )Ф v,

PV (1-gi) fv                      , где αl – объемная доля жидкости.

Источниковый m+ и стоковый m- члены в уравнении (6) определяют соответственно скорости испарения и конденсации. Они зависят от многих факторов и их формулировка в настоящее время не унифицирована для различных конструктивных и режимных параметров, встречающихся в различных прикладных задачах. Обзор методов определения этих членов приведен в [8]. Здесь предполагается определение этих членов с помощью уравнения Рэлея-Плессета, учитывающего вязкость жидкости и поверхностное натяжение при пульсациях пузырька в жидкости [9, 10]. Таким образом, источниковый и стоковый члены определяются по соответствующим уравнениям:

m

- F .

3 а-» i A EZ E Z E f T Toj R B 3 m max I     P l       ) ’

m - = F ^c

3(1 a 1) .

RB

у 3

min

Г P - P ( T )

I      P l

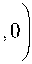
Эмпирические постоянные F v и F c в этих уравнениях учитывают тот факт, что процессы конденсации и испарения имеют различные временные масштабы - процесс конденсации протекает медленнее испарения [11]. Присутствующие в воде сферические пузырьки неконден-сирующегося газа являются зародышами для образующихся паровых полостей. Для расчетов принимались следующие значения: объемная доля неконденсированного газа в воде α nuc равна 540^-5, а радиус зародышей кавитации R b = 10^-6 м, F v = 50 и F = 0,01.

Для учета турбулентности использовалась k – ε модель. Уравнения переноса кинетической энергии турбулентности k и ее диссипации ε имеют вид

■

⁵ X j      ⁵ X j

и + Hl )dkL' f a dxx k 7 j J

+ G - Pm 8

d( ftu^_ 8

8 X j       8 x

«  иЛбЛ   £     2

Il + t j   — C2P J

где скорость генерации турбулентности G и тензор напряжений Рейнольдса определяются по соответствующим уравнениям:

^G = ^т _ц

д ui

8 xj ’

^T ij =^{- P}n uiu j = P T

,5 x j^ B x, ]- P 3 j

Турбулентная вязкость μ T определяется по формуле

ц t —

P m C , k ²

£

Эмпирические константы имеют следующие значения: qi =1,0; о_£=1,3; C _t = 1,44; C ₂ = 1,92, C "

Объемная доля фазы может изменяться от нуля до единицы в зависимости от занимаемого пространства в двухфазном потоке. Согласно тому, что фазы должны полностью заполнять весь объем, получаем уравнение

Е а= 1-                                                   (16)

Геометрия и граничные условия

На рисунке 2 представлена геометрия рабочего участка суперкавитационного испарителя с обозначением граничных условий. В рабочем участке длиной Н = 470 мм и диаметром D ₀ = 70 мм установлен кавитатор на расстоянии h = 50 мм от входа в рабочий участок. В качестве кавитатора использовался конус с углом раствора 53 °. Исследования проводились в условиях, когда влияние стеснения потока на форму и размеры каверны существенно. Степень – 501 –

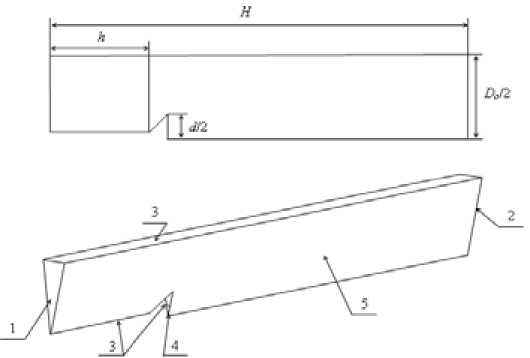
Рис. 2. Геометрия рабочего участка суперкавитационного испарителя с обозначением граничных условий: 1 и 2 соответственно вход и выход из рабочего участка, 3 – стенки, 4 – отбор пара из каверны, 5 – условия симметрии

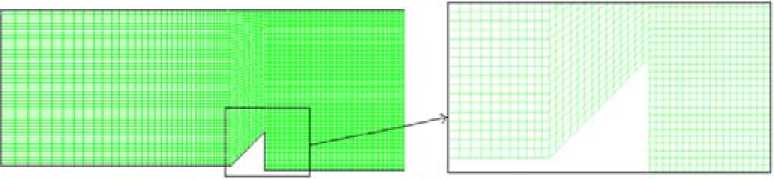
Рис. 3. Расчетная сетка стеснения потока d/D0 принималась равной 0,24. Через трубку, расположенную вдоль оси рабочего участка, осуществлялся отбор пара из каверны.

Как видно из рис. 3, расчетная сетка состоит из гексаэдрических элементов и имеет ^специальное сгущение в месте предполагаемого образования каверны. Задача рассматривается в стационарной осесимметричной постановке. Для замыкания системы уравнений принимаем следующие граничные условия: на входе в рабочий участок задана скорость 6 м/с, линейный масштаб 0,005 и интенсивность турбулентности 0,03, объемные доли пара и воды 0,0 и 1,0 соответственно, а на выходе – давление равно 147 кПа. На стенках скорость задана равной нулю. Расчеты проводились для воды, температура которой принималась равной 110 ° С, что соответствует максимальной температуре воды на входе в первую ступень испарения большинства современных испарительных установок [12]. В основании кавитатора осуществлялся отбор пара в количестве 0,0414 кг/ч. Теплофизические параметры воды и пара принимались согласно [2].

Результаты численного исследования

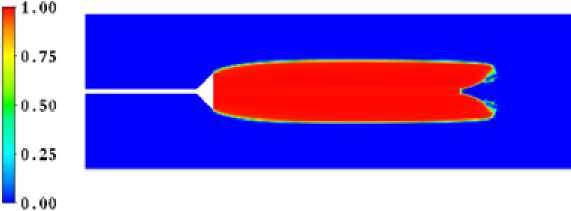
В результате вычислений были получены поля скоростей, давлений, температуры и доли пара в смеси, а также распределение кинетической энергии и скорость диссипации. Частично результаты представлены на рис. 4.

а

б

155000[Ра]

Рис. 4. Результаты численного моделирования: а – доля пара; б – температурное поле; в – поле давлений

На рисунке 4 а отображена зависимость объемной доли пара в потоке смеси от координат. Как видно, область фазового перехода имеет довольно тонкую границу, что объясняется высокими градиентами давления в этой области (рис. 4 в ). Расчетная длина каверны для заданных условий составила 12 мм. Как видно из рис. 4 б , температура в каверне уменьшилась относительно температуры на входе в рабочий участок приблизительно на 38 °С, а в области замыкания каверны выросла на 24 °С. Данный эффект объясняется повышением давления в этой области и процессом вихреобразования. Таким образом, в небольшом объеме в месте замыкания каверны образуется достаточно высокое тепловыделение за счет конденсации пара, что является причиной роста температуры в этой области. Как показали результаты расчета, заданный отбор пара из каверны не разрушает ее, что объясняется интенсивным испарением на ее поверхности и устойчивой граничной динамикой.

Заключение

В статье представлена аналитическая зависимость числа кавитации от температуры, из которой видно, что с уменьшением температуры интенсивность кавитации в потоке воды по-– 503 – нижается. В случае повышения температуры воды, поступающей в рабочий участок суперкавитационного испарителя, и увеличения пароотбора из каверны влияние термодинамических эффектов усиливается. В этой связи разработана математическая модель, позволяющая проводить расчетные исследования кавитационных течений с учетом термодинамических эффектов. Проведено моделирование рабочих процессов суперкавитационного испарителя. Полученные расчетные результаты хорошо согласуются с экспериментальными данными. Суперкавитационный метод является перспективным способом опреснения воды и требует дальнейшего изучения и развития.