Численное исследование процессов вытеснения нефти водой из пористой среды
Автор: Хайруллин А.А., Мамчистова Е.И., Чикиров Р.Р.
Журнал: Научный форум. Сибирь @forumsibir
Рубрика: Природопользование природопользование
Статья в выпуске: 4 т.2, 2016 года.
Бесплатный доступ
Рассмотрена задача о несмешивающемся вытеснении нефти водой в пористой среде при отсутствии в ней подвижной газовой фазы. Исследованы особенности процессов фильтрации в системе «нефть-вода», характерных для модели фронтального вытеснения.
Многофазная фильтрация, моделирование, численные методы
Короткий адрес: https://sciup.org/140220388
IDR: 140220388
Текст научной статьи Численное исследование процессов вытеснения нефти водой из пористой среды
Как показывает многолетний мировой опыт, большинство месторождений разрабатывается на основе различных систем заводнения. Предсказание осложнений в разработке водонефтяных зон строится на тщательном изучении закономерностей движения пластовых флюидов в различных геологических условиях строения залежей нефти и при различном техногенном воздействии на них.
Постановка задачи. Рассматривается процесс фильтрации двухфазной жидкости, состоящей из воды и нефти, сквозь пористую среду. Пласт, первоначально насыщен нефтью и удерживаемой капиллярно (связанной) водой, считается однородным и тонким, что позволяет использовать для анализа двухмерную модель. В рамках данной задачи будем считать, что массообмен между нефтью и водой не происходит. Часть связанной воды (остаточная во-донасыщенность) занимает наиболее мелкие поры, в которых капиллярные силы значительно превосходят гидродинамические, она останется неподвижной во всем физически достижимом диапазоне депрессий.
Построение математической модели рассматриваемого процесса начнем с записи уравнения сохранения массы нефти и воды в пористой среде, которые имеют вид [1]:
d('. '+divри)+q i = 0 i=ow (1) о t
где m - пористость, S i - насышенность i - той фазы, p i , и i - плотность и скорость фильтрации нефти и воды соответственно.
В классической теории фильтрации законом движения является закон Дарси, который в случаи двухфазной фильтрации называется обобщенным законом Дарси и имеет вид:
kf
U = gradp i=o,w (2)
Pi где k - абсолютная проницаемость образца, цi -динамическая вязкость соответствующей фазы, f,- -относительные фазовые проницаемости, характеризующие зависимость скорости фильтрации от водо-насыщенности.
Для описания выбранного физического процесса достаточно ограничиться двумерным видом уравнений (1)-(2), Обозначим S=S w значение водо-насыщенности и сложим (1) и (2) уравнение, исключив члены, отвечающие за источники и стоки. Пренебрегая разностью давлений фильтрующихся фаз (капиллярным давлением) и сжимаемостью флюида, окончательно имеем:
ной области, а на боковых гранях равенство нулю расходов, что обеспечит условие непротекания этих границ:
x=0 S=S 0 (y,t), P=P0(y,t);
x L
,
P=P
tx
(y,t),
P
lx
0;
y={0,L y } dP/dy=0.
Преобразуем систему (3) к виду, более удобному для построения численного решения [2]. В итоги получим эллиптическое уравнение для определения давления
|[kx ( fw + k £9x L V Pw Po )dx
d
+ — dy
<
k y
(fw+A 'E
VPw PoA^y,
= 0
и гиперболическое уравнение для водонасы-
щенности
dS d m — + —
dt dx
fw 9P
P w 9 x
+± dy
: Л 5P y Pw 9y
= 0
Численная реализация математической модели. Для численного решения будет использоваться метод контрольных объемов [3], так как полученный подобным образом дискретный аналог выражает закон сохранения для конечного контрольного объема точно так же, как дифференциальное уравнение выражает закон сохранения для бесконечно малого контрольного объема. Для расчета будет использоваться стандартная пятиточечная аппроксимация по координатной сетке и полностью неявную по времени.
Дискретизации аналог уравнение (5) примет вид:
n+1 pn +1 n+1 pn+1 n+1 pn+1 n+1 pn+1 n+1 pn+1q ai+0.5,jp+1,j + ai-0.5,Ji-1,j + ai,j+0.5Pi,j+1 + ai,j-0.5Pi,j-1 + ai,j Pi,j 0
5S .
m— + divu = 0
5t w
f
U =- k — grad (p)
P i
л
. (If f A
div k fw + fo- gradP = 0
V V pw po ) )
Sw + So = 1
i = o, w
(7), где:
a^5,j = (fl10.,j I Pw + fni+o.5,j I Po )TRANX j, a^,, = (fw*10.5., I Pw + fo"i-»,5,, I Po "T-IANX--,j,
a - = (f^,.,, । Pw + fnW5 । Po 'T'RANYT,.,. , a”+;«.5 = (гр,-0.51Pw + foni+j-0.5 IPo)TIANYi,j- n+1 n+1 . n+1 . n+1 . n+1
ai , j = ai + 0.5, j + ai - 0.5, j + ai , j + 0.5 + ai , j - 0.5
Проводимости - статические параметры, зависят только от геометрии сетки и характеристик пористой среды.
TRANX i + ,j =, kxM kf ,u,i, — Ai ++j (9)
k x , i , j ^ x i + 0.5, j + kx , i + 1, j ^ x i - 0.5, j
Начальным условием задачи (3) будет начальное распределение насыщенности t=0 S=Sw(x,y)
В качестве граничных условий примем постоянное давление на правой и левой границе расчет-
TRANX i - , j , k
______________x,i,J,k ^x,i-1,J,k_______________ Д к + к i-0'5, j x, i, j , PAxi-0.5, j + ^x, i -1, j, kuxi ,+0.5 j
k . . • k
TRANY,. + =----------- y ’ i ’ j y ’ i ’ j + 1 ----------A /+05
i , j + i , j + 0.5
ky , i , jUx i , j + 0.5 + ky , i , j +16 M 7, j - 0.5
k • k
TRANY . =----------- y , i ’ j y , i ’ j - 1 ----------A,0 5
-
i , j - i , j - 0.5
-
y, i, j^i, j - 0.5 + y, i, j - 1, v-xi, j + 0.5
A – площади соответствующих граней
Функции относительных фазовых проницаемо-стей (ОФП) определяются как функции от насыщенности блока, из которого направлен поток:
fn+1( 1 ,£) =
fr (Sn+1), если PlQ > P ,.,
J r 1 1 ’ 9 i , j r = o, w (13)
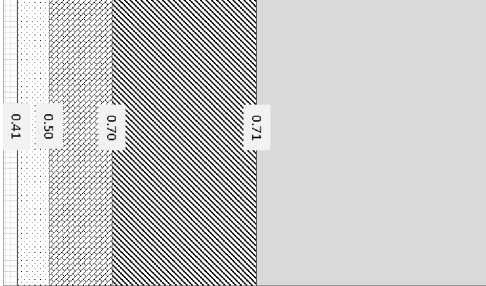
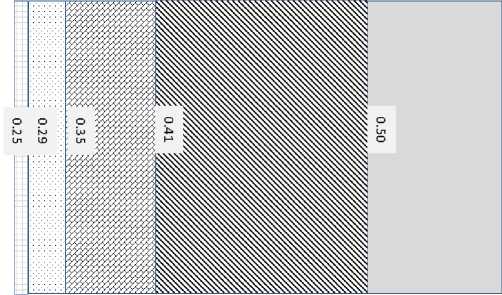
fr(Sn'), если P,6 Рис. 1. Функции ОФП в системе «нефть-вода». Дискретизировав уравнение (6) получаем явное уравнение для водонасащенности: оn+1 _ nn Si, j = Si, j ^“ dt • Ln +1 i, j Vi, Jm Результаты численных расчетов. На рис. 2. Показано изменение водонасыщенности по длине пласта в различные моменты времени. n+1 Здесь L – вспомогательной разностный опе- ратор представляющий разность потоков водной фазы, дискретизируется аналогично уравнению (7). Уравнение (7) можно разрешить относительно давления при известных насыщенностях одним из итерационных методов. Затем с использованием уравнения (14) явным методом находятся насыщенности. Использованный метод разделения исходной системы на уравнение для давления и уравнение для насыщенности называется IMPES-методом [2] (Implicit Pressure Explicit Saturation) Параметры моделируемой системы. Для проведения численных экспериментов систему уравнений необходимо дополнить исходными данными приведенными в табл. 1 и зависимостями относительных фазовых проницаемостей воды и нефти от водонасыщенности (рис. 2). Таблица 1 0 200 400 600 800 1000 Длина пласта, м Рис. 2. Изменение насыщенности по длине пласте вдоль линии вытеснения. На рис. 3-4 представлены поля распределения нефтенасыщенности в различные моменты времени. Параметры моделируемой системы Параметр Значение Ед.измерения Lx 1000 М Ly 600 М m 0,15 д.ед So 0,7 д.ед µo 10 мПа*с µw 1 мПа*с Рис. 3. Поле нефтенасыщенности, начало процесса вытеснения. Рис. 4. Поле нефтенасыщенности, конечный момент времени. Не смотря на то, что нефть и вытесняющий ее агент движется одновременно в пористой среде, полного вытеснения нефти замещающими ее агентами никогда не происходит, так как ни газ, ни вода не действуют на нефть как «поршни». Вследствие неоднородности размеров пор в процессе замещения вытесняющая жидкость с меньшей вязкостью неизбежно опережает нефть. С увеличением водо-насыщенности, увеличивается количество воды в потоке в связи с возрастанием эффективной проницаемости породы для воды. При этом нефть уже не вытесняется из пор, а, скорее, увлекается струёй воды. Таким образом, по длине пласта образуется несколько зон с различной водонефтенасыщенно-стью.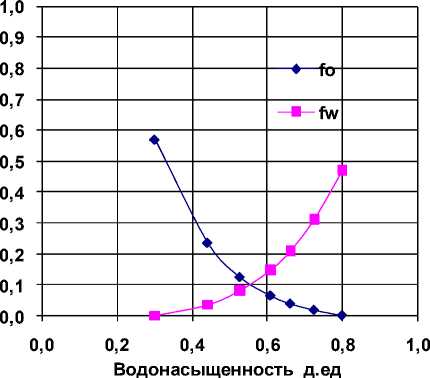
Список литературы Численное исследование процессов вытеснения нефти водой из пористой среды
- Басниев К.С., Дмитриев Н.М., Каневская Р.Д., Максимов В.М. Подземная гидромеханика. -М.-Ижевск: ИКИ, 2006. -488 с.
- Азиз Х., Сеттари Э.Математическое моделирование пластовых систем гидромеханика. -М.: Недра, 1982. -407 с
- Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. -М.: Энергоатомиздат, 1984. -152 с.


