Численное исследование работы замкового соединения стеновых панелей на растяжение до образования трещин

В 2014 году АО «ЦНИИЭП жилища» была предложена новая конструкция бессварных вертикальных стыков крупнопанельных зданий (замковое соединение), воспринимающих растягивающие и сдвигающие усилия. Замковое соединение представляет собой монолитный шпоночный стык с механическим зацеплением П-образной скобы из арматурной стали за петлевые выпуски на торцах смежных панелей с усилением стальной пластиной, соединяющей концы скобы от разгибания под действием нагрузки [1]. Общий вид стыка представлен на рис. 1.

В соответствии с предварительными исследованиями, проведенными разработчиками, стык обладает значительными прочностными и жестко- стными характеристиками, может использоваться при проектировании зданий с широким шагом несущих конструкций и для проектирования в сейсмических районах [1–3].

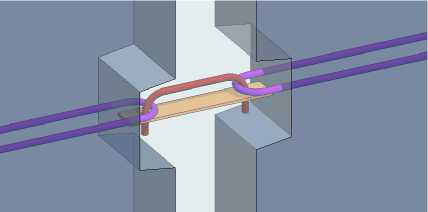
Рис. 1. Общий вид замкового соединения стеновых панелей

Межпанельные стыки обеспечивают совместную работу элементов крупнопанельного здания. При создании расчетной схемы крупнопанельного здания необходимо учитывать, что связи между панелями не являются абсолютно жесткими или шарнирными, необходимо учитывать их податливость. В современных программных комплексах для расчета строительных конструкций стены и перекрытия моделируются плоскими конечными элементами, а связь между ними осуществляется с использованием специальных конечных элементов упругой связи между узлами (например, КЭ 55 или КЭ 255 в ПК «Лира-САПР»), с помощью которых учитывается работа стыков [4–8]. При этом необходимо знать его жесткость и предельное усилие при сдвиге, растяжении и сжатии.

В данной статье рассматривается работа стыка на растяжение. Поскольку в нормативной и справочной литературе отсутствует универсальная методика расчета характеристик стыков при растяжении [9], необходимо его экспериментальное и численное исследование.

В результате экспериментального исследования натурных образцов стыка на растяжение была выявлена его двухэтапная работа [10]. До появления трещин в образце в области соединения скобы с петлей стык работает с повышенной жесткостью. Предполагается, что до появления значительных деформаций в образце (до появления трещин в бетоне образца) происходит выборка зазора между скобой и петлей, работа стыка характеризуется выдергиванием петли из бетона омоноличивания стыка. После появления трещин в бетоне образца, за счет значительных деформаций образца работа стыка определяется работой скобы и пластины с последующим разрушением вследствие разрыва скобы.

Двухэтапную работу стыка следует учитывать при расчете на особые воздействия (например, сейсмические), так как в этом случае при достижении усилия образования трещин происходит ослабление связей без разрушения стыка и снижение усилий от сейсмической нагрузки за счет увеличения общей деформативности здания [3].

При основных эксплуатационных нагрузках стык работает в соответствии с первым этапом (до образования трещин). В этом случае прочность и жесткость стыка зависят от класса бетона образца, что было показано при испытании натурных образцов. Подробный анализ результатов экспериментального исследования замкового соединения стеновых панелей при растяжении представлен в работе [10].

Целью работы является выявление характера взаимодействия стального петлевого выпуска и бетона омоноличивания стыка для оценки его расчетных характеристик (жесткости и трещиностой-кости).

Исследование проводится с использованием метода конечных элементов. Для определения ха- рактеристик стыка производится расчет численных моделей стыка.

Методика исследования

Как отмечено выше, до образования трещин в бетоне образца работа стыка характеризуется работой петлевого выпуска на выдергивание из бетона. С целью проведения численного анализа работы образца была построена плоская конечноэлементная модель замоноличенной в бетоне петли. Размеры модели приняты в соответствии с испытанными образцами [10]. Выпуски выполнялись из арматуры А500С, которая обладает значительной прочностью и при этом является достаточно пластичной, что позволяет применять ее в качестве петель [11, 12].

Модель строилась в ПК «Лира-САПР»: петля смоделирована стержневыми конечными элементами (КЭ10) круглого сечения, бетон образца – конечными элементами плоского напряженного состояния (балки-стенки – КЭ21, КЭ22, КЭ30), контакт между петлей и бетоном – конечными элементами упругой связи с предельным усилием (КЭ255). Размеры конечных элементов приняты от 2,5 до 8 мм.

Диаметр сечения конечных элементов петли принимается равным номинальному диаметру арматуры, модуль упругости – модулю упругости арматуры в соответствии с СП 63.13330.2012 [13].

Толщина конечных элементов бетона принята равной высоте опытных образцов (высоте шпонки – 13 см), в местах расположения петли толщина бетона уменьшена на величину средней по площади толщины сечения петли. Модуль упругости бетона элемента принят равным начальному модулю упругости соответствующего класса, коэффициент поперечной деформации Пуассона принят равным 0,2 [13].

Конечные элементы упругой связи моделировали сцепление арматуры петли с бетоном. Конечный элемент характеризуется жесткостью связи на сдвиг (жесткость в продольном направлении) и на растяжение-сжатие (жесткость в поперечном направлении). Жесткость связей определялась на основании исследования А.А. Карякина [14], использовался начальный модуль сцепления арматуры с бетоном. Жесткость элементов упругой связи принималась равной среднему начальному модулю сцепления по различным точкам по длине стержня. Так как вычисления [14] основаны на экспериментальном исследовании арматуры А-III (A400) [15], модуль сцеплениябыл скорректирован для учета особенностей профиля арматура А500С [16]. Для корректировки использовались исследования М.М. Холмянского [17], в соответствии с которым жесткость сцепления прямо зависит от отношения глубины профилировки к ее шагу [17].

Работа упругих связей контакта на растяжение в направлении, нормальном к продольной оси петли, не учитывается (принято нулевое предельное усилие на растяжение).

В силу симметрии стыка рассматривается расчетная схема половины образца, на узлы на оси симметрии накладываются линейные связи по направлению оси X (перпендикулярно оси симметрии) и угловые связи вокруг оси Y (в плоскости схемы). На концах петли смоделирована скользящая заделка (приложены угловые связи вокруг оси Y и линейные по направлению оси Z, перпендикулярной направлению действия нагрузки). Расчетная схема представлена на рис. 2.

Для сопоставления результатов численного моделирования с результатами экспериментального исследования [10] расчет выполнялся для образцов с диаметром петли 16 мм из бетона классов В30 и B40 (как наиболее близких к фактическому классу бетона исследованных образцов).

Для определения характеристик стыков сдру-гими параметрами (диаметром петлевых выпусков и класса бетона омоноличивания) такжестроились соответствующие численные модели. Были построены модели для стыков с диаметром петли 12 и 14 мм и бетона омоноличивания класса В15– В40.

Расчет производился при общей растягивающей нагрузке 1 т, приложенной по 0,5 т к каждому концу петли.

Результаты исследования и их анализ

В результате расчета модели стыка были определены максимальные перемещения узлов в направлении действующей нагрузки (вдоль оси Х), эпюры внутренних силовых факторов в конечных элементах петли, главные и эквивалентные напряжения в бетоне стыка.

Для сопоставления с экспериментальными данными рассмотрены модели стыков с петлей диаметром 16 мм. Результаты расчета модели стыка из бетона В30 представлены на рис. 3–6.

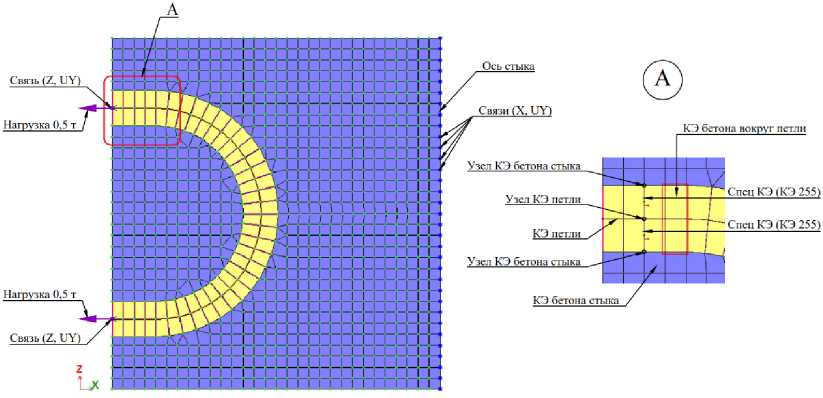
Рис. 2. Расчетная схема половины стыка в ПК «Лира-САПР»

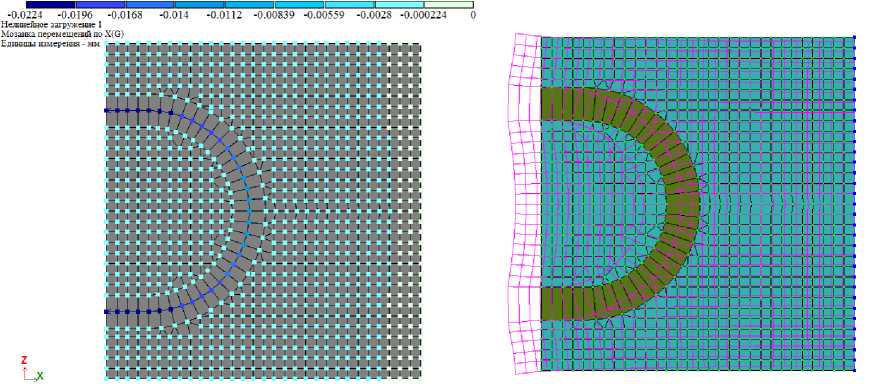
Рис. 3. Перемещения узлов стыка (бетон В30): мозаика перемещений узлов вдоль оси Х (слева) и деформации бетона образца поверх исходной схемы (справа)

Максимальные перемещения узлов (перемещения концов петли) составили 0,0224 мм и 0,0195 мм соответственно для класса бетона В30 и В40. Жесткость стыка на растяжение в целом определяется как отношение приложенной к концам петли нагрузки к удвоенному перемещению (так как рассматривается половина стыка) концов петли и составила для бетона В30 и В40 соответственно K_t = 22,35 т/мм и K_t = 25,64 т/мм.

В обоих случаях (в образце из бетона В30 и в образце из бетона В40) максимальные эквивалентные напряжения (по IV теории прочности [18]) возникают на концах петель (в местах приложения нагрузки). Усилия в петлях составили: N = 0,477 т, M = 0,00121 т·м, Q = 0,0729 т – для образца В30; N = 0,476 т, M = 0,00115 т·м, Q = 0,0694 т – для образца В40.

Максимальное эквивалентное напряжение на концах петли равно максимальному растягивающему напряжению от действия продольной силы и изгибающего момента и составило при нагрузке 1 т для образцов из бетона В30 и В40: о = 5390 т/м2 (52,86 МПа) и о = 5233 т/м2 (51,32 МПа) соответственно. При расчетном сопротивлении арматуры А500 (Rs = 435 МПа [2]) предельная нагрузка по несущей способности (по достижении предела текучести) петли составляет 8,229 т и 8,477 т для стыка из бетона В30 и В40 соответственно.

Для оценки трещиностойкости бетона образца используются главные и эквивалентные напряжения. Эквивалентные напряжения определяются по теории прочности Г.А. Гениева [19] и вычисляются в ПК «Лира-САПР» автоматически, в качестве предельных напряжений при растяжении и сжатии приняты нормативные сопротивления бетона в соответствии с СП [13]. Мозаики главных и эквивалентных напряжений для образца из бетона В40 представлены на рис. 5 и 6 соответственно. Также на рис. 6 показано направление главных площадок, в которых возникают максимальные напряжения, по которым можно судить о направлении трещин.

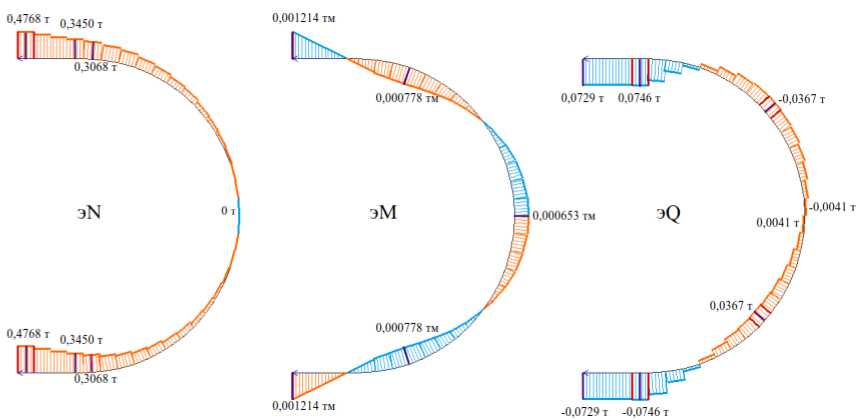
Рис. 4. Эпюры усилий в петле (бетон В30)

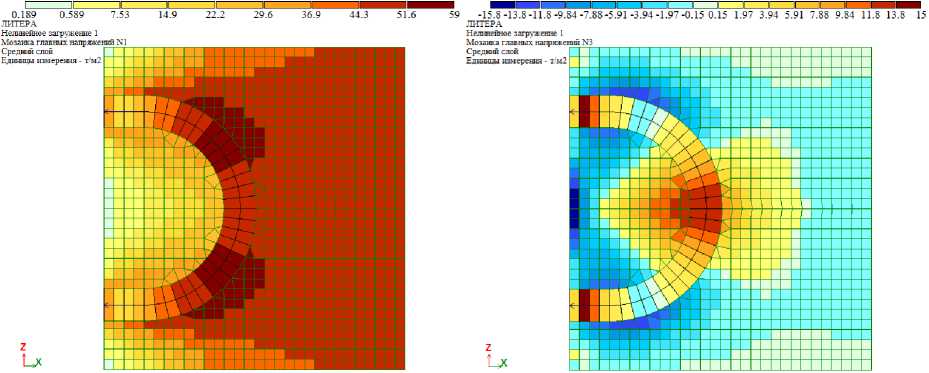
Рис. 5. Главные напряжения в бетоне образца (бетон В30)

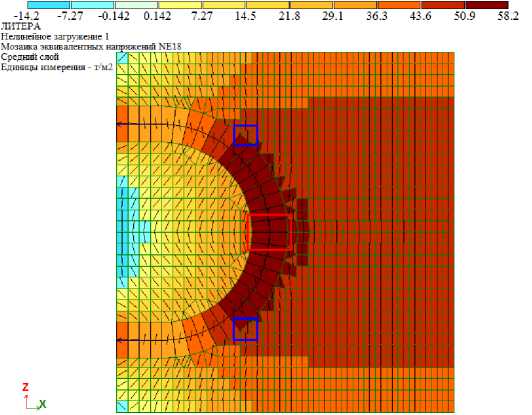
Рис. 6. Эквивалентные напряжения в бетоне образца по теории Г.А. Гениева (бетон В30)

Максимальные эквивалентные напряжения в образцах при нагрузке 1 т составили 58,16 т/м2 и 57,65 т/м2, возникают на продольной оси стыка в месте загиба петли (на рис. 6 элементы выделены красной рамкой). Таким образом, в соответствии с теорией прочности Гениева усилие образования трещин в бетоне образца составило 3,06 т и 3,71 т – для бетона В30 и В40 соответственно.

Для определения напряжений, соответствующих образованию трещин в бетоне, также использовано условие образования трещин Н.И. Карпенко [20]. Условие образования трещин при плоском напряженном состоянии преобразовано в условную теорию прочности с эквивалентным напряжением:

σ eq

где σ _max

σ max

≤ R bt , n , k_p

– максимальное главное напряжение в точке; Rbt,n – нормативное сопротивление бетона растяжению; kp – коэффициент, учитывающий влияние минимального нормального напряжения σmin на образование трещин, зависит от минимального нормального напряжения, прочности бетона и толщины элемента [20].

Максимальные эквивалентные напряжения в бетоне по теории Н.И. Карпенко составили 58,94 т/м2 и 59,08 т/м2 для образцов из бетона В30 и В40 соответственно и возникают ближе к краям образца (на рис. 6 элементы выделены синими рамками). Образование трещин в образцах в соответствии с теорией Карпенко происходит при нагрузках 3,03 т и 3,62 т.

Усилия образования трещин, определенные по теориям Г.А. Гениева и Н.И. Карпенко, различаются незначительно, но теория Н.И. Карпенко дает меньшее значение.

В результате расчета можно сделать вывод о том, что численное моделирование согласовывается с результатами эксперимента. Разница экспериментальных значений усилия образования трещин и жесткости стыка и результатов численного моделирования для образцов из бетона В40 оказалась незначительной (не более 10 %). Для образцов из бетона В30 результаты сильно разняться за счет выбивающихся значений в экспериментальном исследовании, что требует проведения дополнительных испытаний. Также стоит отметить, что максимальные эквивалентные напряжения возникают в области вершины петли, что совпадает с областью возникновения трещин в испытанных образцах [10].

Для оценки прочности и жесткости стыков с другими размерами петель при различных классах бетона выполнялся расчет соответствующих моделей. Перемещения узлов, главные и эквивалентные напряжения в бетоне для образца из бетона В30 при диаметре петлевого выпуска 12 мм при нагрузке 1 т приведены на рис. 7–9.

Результаты при других параметрах стыка приведены в табл. 1 и 2 (где B – класс бетона стыка, Δ _max – максимальное перемещение концов петли, σ _eq (Г) – эквивалентное напряжение по теории Гениева, σ eq (К) – эквивалентное напряжение по теории Карпенко, σ s – напряжение на концах петли, K t – жесткость стыка на растяжение, P crc (Г) – нагрузка образования трещин по теории Г.А. Гениева, P crc (К) – нагрузка образования трещин по теории Н.И. Карпенко, P_yl – нагрузка, соответствующая пределу текучести петли).

Результаты расчета также показывают увеличение нагрузки образования трещин и жесткости при увеличении класса бетона стыка. При этом можно заметить, что эта зависимость является практически линейной. Также стоит отметить, что увеличение диаметра петли приводит к увеличению

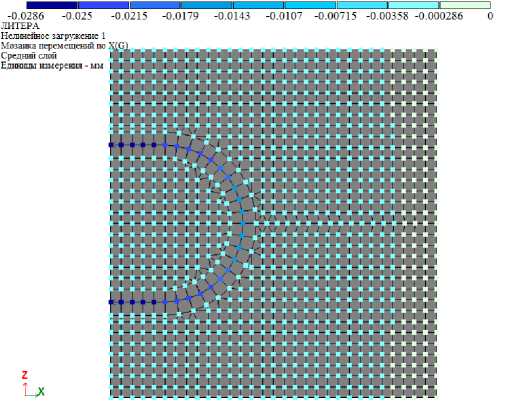
Рис. 7. Мозаика перемещений узлов вдоль оси Х (бетон В30, петлевой выпуск 12 мм)

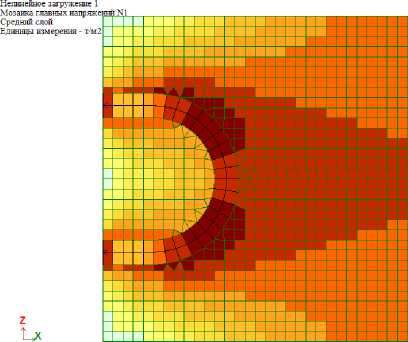
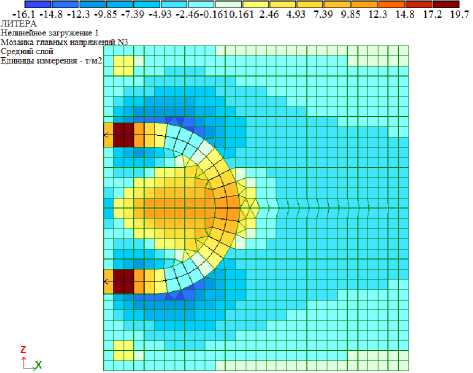
Рис. 8. Главные напряжения в бетоне образца (бетон В30, петлевой выпуск 12 мм)

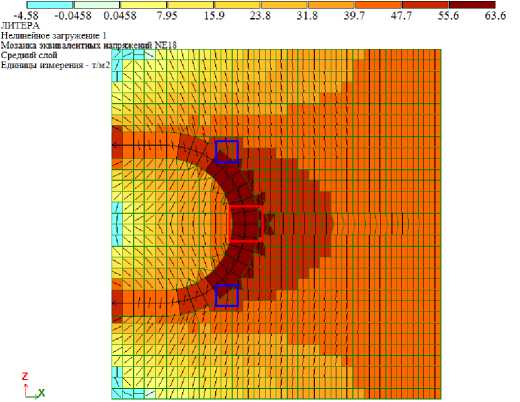
Рис. 9. Эквивалентные напряжения в бетоне образца по теории Г.А. Гениева (бетон В30, петлевой выпуск 12 мм)

Таблица 1

Результаты расчета стыка с петлевыми выпусками 12 мм

B, МПа	Δ max , мм	σ eq (Г), т/м2	σ eq (К), т/м2	σ s, МПа			Kt , т/мм	P crc (Г), т	P crc (К), т	P yl , т
				от N	от M	сумм.
15	0,0382	65,03	66,72	41,12	42,94	84,06	13,10	1,72	1,68	5,17
20	0,0341	64,46	66,78	41,07	41,00	82,07	14,65	2,14	2,06	5,30
25	0,0311	64,00	66,83	41,03	39,24	80,27	16,09	2,47	2,37	5,42
30	0,0286	63,57	66,87	40,99	37,63	78,62	17,48	2,81	2,67	5,53
35	0,0266	63,16	66,91	40,95	36,17	77,12	18,77	3,15	2,97	5,64
40	0,0250	62,88	66,94	40,91	34,81	75,72	20,02	3,41	3,20	5,74

Таблица 2

Результаты расчета стыка с петлевыми выпусками 14 мм

B, МПа Δmax, мм σeq (Г), т/м2 σeq (К), т/м2 σs, МПа Kt, т/мм Pcrc (Г), т Pcrc (К), т Pyl, т от N от M сумм. 15 0,0319 60,26 61,15 30,38 35,03 65,41 15,66 1,86 1,83 6,65 20 0,0285 59,82 61,21 30,35 33,59 63,94 17,52 2,30 2,25 6,80 25 0,0260 59,44 61,27 30,32 32,29 62,61 19,24 2,66 2,58 6,95 30 0,0239 59,07 61,32 30,29 31,09 61,38 20,88 3,02 2,91 7,09 35 0,0223 58,71 61,37 30,27 29,99 60,26 22,43 3,39 3,24 7,22 40 0,0209 58,47 61,42 30,24 28,97 59,21 23,92 3,66 3,49 7,35 жесткости стыка и предельной нагрузки до образования трещин.

Предельное усилие по образованию трещин и жесткость стыка значительно превосходят аналогичные значения для стандартных петлевых стыков, в которых при небольших нагрузках происходит разгибание скобы с дальнейшим разрушением бетона стыка [21]. В замковом соединении пластина препятствует разрушению бетона скобой, что позволяет на первом этапе не рассматривать работу элемента замка до выборки зазора между ними и петлевыми выпусками.

Заключение

При численном исследовании замкового соединения стеновых панелей на растяжение до образования трещин были произведены расчеты конечно-элементных моделей замкового стыка. Результаты расчета были сопоставлены с результатами испытаний натурных образцов, обнаружено сходство как в расположении трещин, так и в численных значениях характеристик стыка. Также определены характеристики жесткости и трещино-стойкости стыка при различных классах бетона стыка и диаметрах петлевых выпусков. Результаты исследования могут быть использованы при расчете и проектировании крупнопанельных зданий.

Дальнейшие исследования могут быть направлены на уточнение рассмотренной методики, а также на исследование работы стыка с трещинами для использования в расчетах зданий при особых воздействиях.

При проведении исследования использовались ресурсы ПВК лаборатории суперкомпьютерного моделирования ЮУрГУ.