Численное исследование режимов работы одноступенчатого поточного газогенератора с паровоздушным дутьем

Повышение технической и экологической эффективности использования твердого топлива в энергетике является важной научно-технической проблемой [1]. Одним из способов ее решения может стать переход с парового цикла на более эффективный парогазовый цикл за счет газификации угля (IGCC) [2]. Большая часть таких станций использует поточные газогенераторы, в которых угольная пыль газифицируется в несущем потоке дутья [3–5]. В качестве дутья обычно используется парокислородная смесь, однако существуют и реакторы, использующие воздух. С одной стороны, при этом удается снизить собственные нужды станции за счет отказа от воздухоразделения; с другой стороны, при этом существенно возрастает нагрузка на дутьевые агрегаты и, что особенно важно, изменяются параметры термодинамически и кинетически оптимальных режимов (из-за необходимости нагрева инертного азота и уменьшения концентрации газов-реагентов в реакционной зоне газогенератора). Вопросы реализации высокотемпературного подогрева обсуждаются в работах [6, 7].

Последняя проблема может быть решена с помощью подогрева дутья до высоких температур аналогично процессам MILD-сжигания [8–11]. В этом случае снижаются потери, связанные с нагревом системы до температуры воспламенения, а также частично компенсируются энергетические затраты на эндотермические реакции образования горючих газов. В работах [12] подогрев дутья был предложен для двухступенчатого реактора. Однако при достаточно высокой температуре дутья можно ограничиться и одной стадией. В настоящей работе с помощью численного моделирования исследуется процесс газификации угля в одностадийном поточном реакторе с нагретым па- ровоздушным дутьем, стационарные режимы работы такого газогенератора в разных условиях и оптимальные режимы в выбранной области параметров.

Математическая модель процесса газификации

В работе используется пространственно одномерная модель процесса газификации угля в потоке, аналогичная моделям [13–16]. При формулировке математической модели принимаются следующие допущения [17, 18]:

• •    скорость сушки лимитируется внешним мас-сообменом с окружающим воздухом;

• •    скорость пиролиза пропорциональна содержанию летучих в частице и зависит от температуры по аррениусовскому закону;

• •    скорость газификации определяется из классического уравнения диффузионно-кинетической теории горения углерода;

• •    теплопотерями реактора можно пренебречь.

Уравнение теплового баланса для угольной частицы записывается следующим образом:

c p m p dT = ^£ ° ⁵ ( Т 4 — ^ТР ) + ^{а 5} ( ^Tg — ^Т р ) — Q w + Q r •

Здесь c p – удельная теплоемкость топлива, Дж/(кг К); m p – масса частицы, кг; T p – температура частицы, К; ε – степень черноты частицы; σ – постоянная Стефана – Больцмана, Вт/(м ² К ⁴ ); S – площадь поверхности частицы, м ² ; T w – температура окружающей среды, К; α – коэффициент конвективного теплопе-реноса, Вт/(м ² К); Q w – теплота испарения влаги, Вт; Q r – теплота химических превращений, Вт.

Скорость сушки вычисляется по формуле jw = KwS (CHq2o - CH2O).

Здесь j w – поток влаги, кг/с; K w – константа скорости сушки, м/с; C – концентрация, кг/м ³ .

Коэффициент конвективного тепло- и массо-обмена для частицы в потоке рассчитывается по формуле Сокольского:

Nu = Sh = 2 + 0,16Re 2/3 .

Здесь Nu – число Нуссельта; Sh – число Шервуда; Re _p – число Рейнольдса для скорости движения частицы относительно несущего потока.

Скорость пиролиза описывается кинетиче- ским уравнением первого порядка:

dmV

d т

— k V exp

—

Ev |

V m .

RT J V

Здесь m V – масса летучих в частице, кг; k_V ⁰ – пред-экспоненциальный коэффициент, 1/с; E V – энергия активации стадии пиролиза, Дж/моль; R – универсальная газовая постоянная, Дж/(моль К). Летучие вещества в модели представляются механической смесью химических элементов, которые после выхода из частицы топлива распределяются по молекулярным формам по условиям химического равновесия.

Скорость реагирования топлива с газообраз- ными окислителями записывается следующим образом:

dm_C d т

^— k eff SC ox ,

где m_С – масса топлива, кг; k_e ff – эффективная константа скорости гетерогенной реакции, м/с; S – площадь поверхности топлива, м ² ; C ox – концентрация окислителя, кг/м ³ .

Эффективная константа скорости выражается через кинетические и массообменные коэффициенты (в предположении, что кинетический порядок реакции по окислителю равен единице) следующим образом:

^kef =

k_Ck_d .

^kC ^{+ k}d '

Здесь k_C – кинетическая константа скорости гетерогенной реакции, м/с; k_d – коэффициент массооб-мена частицы с потоком, м/с.

Кинетическая константа скорости гетерогенной реакции зависит от температуры по экспонен- циальному закону:

^kC = ^kC ^ex P

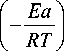
где k_C ⁰ – предэкспоненциальный коэффициент, м/с; E a – энергия активации, Дж/моль.

Химическая кинетика реакций в газовой фазе не рассматривается: полагается, что выходящие в газовую фазу вещества переходят в состояние равновесия. Таким образом, химические превращения описываются с помощью термодинамической модели с макрокинетическими ограничениями на скорость гетерогенных превращений [19, 20]. Та- кой подход применим для высокотемпературных процессов, в которых скорость газофазных процессов достаточно высока по сравнению со скоростью гетерофазных.

Исходные данные и результаты расчетов

Рассматривается трубчатый реактор с производительностью по топливу 100 т/ч, рабочее давление в реакторе 30 атм. Геометрические размеры реактора: длина реакционной зоны 15 м; внутренний диаметр 3 м. Температура топлива, поступающего в реактор, составляет 27 °С; температура пара 323 °С; температура воздуха меняется от 100 до 1000 °С (с шагом в 100 °С). Расход пара меняется от 0 до 0,2 моль/моль углерода, избыток воздуха – от 0,1 до 0,7 от стехиометрического (с шагом 0,05). В качестве топлива используется каменный уголь с характеристиками:

W^r = 2 %; A^d = 15,38 %; V^daf = 29,42 %;

C^daf = 85,45 %; H^daf = 4,86 %;

N^daf = 2,0 %; S^daf = 0,67 %.

Индикаторами режимов выбраны следующие характеристики: химический КПД (доля теплоты сгорания твердого топлива, перешедшая в теплоту сгорания газа), максимальная и конечная температура газа, степень конверсии топлива, а также концентрация горючих компонентов в генераторном газе. Результаты расчетов представлены на рис. 1–6.

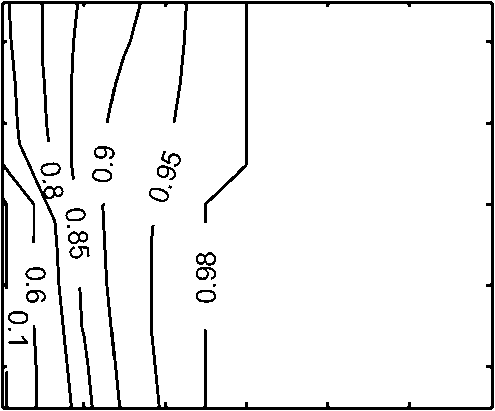
На рис. 1 показаны изолинии химического КПД процесса газификации для разных температур и избытков воздуха. Наблюдается типичная картина: при изменении стехиометрии эффективность процесса имеет выраженный экстремум для каждой фиксированной температуры дутья, соответствующий достаточно полной конверсии топлива (рис. 2) [21, 22]. Рост температуры дутья повышает эффективность только при наличии достаточного количества пара. Расход пара 0,2 моль/моль углерода позволяет повысить максимальный химический КПД газификации с 72 % (для режима без добавок пара) до 84 %. Добавление пара, кроме того, позволяет снизить температуру в ядре факела и на выходе из реактора (рис. 3, 4).

В области низких значений избытка окислителя и невысоких температур химический КПД резко падает: в этой области происходит окислительный пиролиз с неустойчивым температурным режимом, при этом наблюдается большой недожог (см. рис. 2). Увеличение избытка окислителя сверх оптимальных значений (0,3–0,4) приводит к окислению горючих компонентов, что также приводит к снижению эффективности, причем эта зависимость практически одинакова для всех расходов пара (см. рис. 1). Как видно из рис. 5, области параметров с максимальной концентрацией СО смещены в область пиролиза, в то время как максимум образования Н2 соответствует максимуму химического КПД (рис. 6).

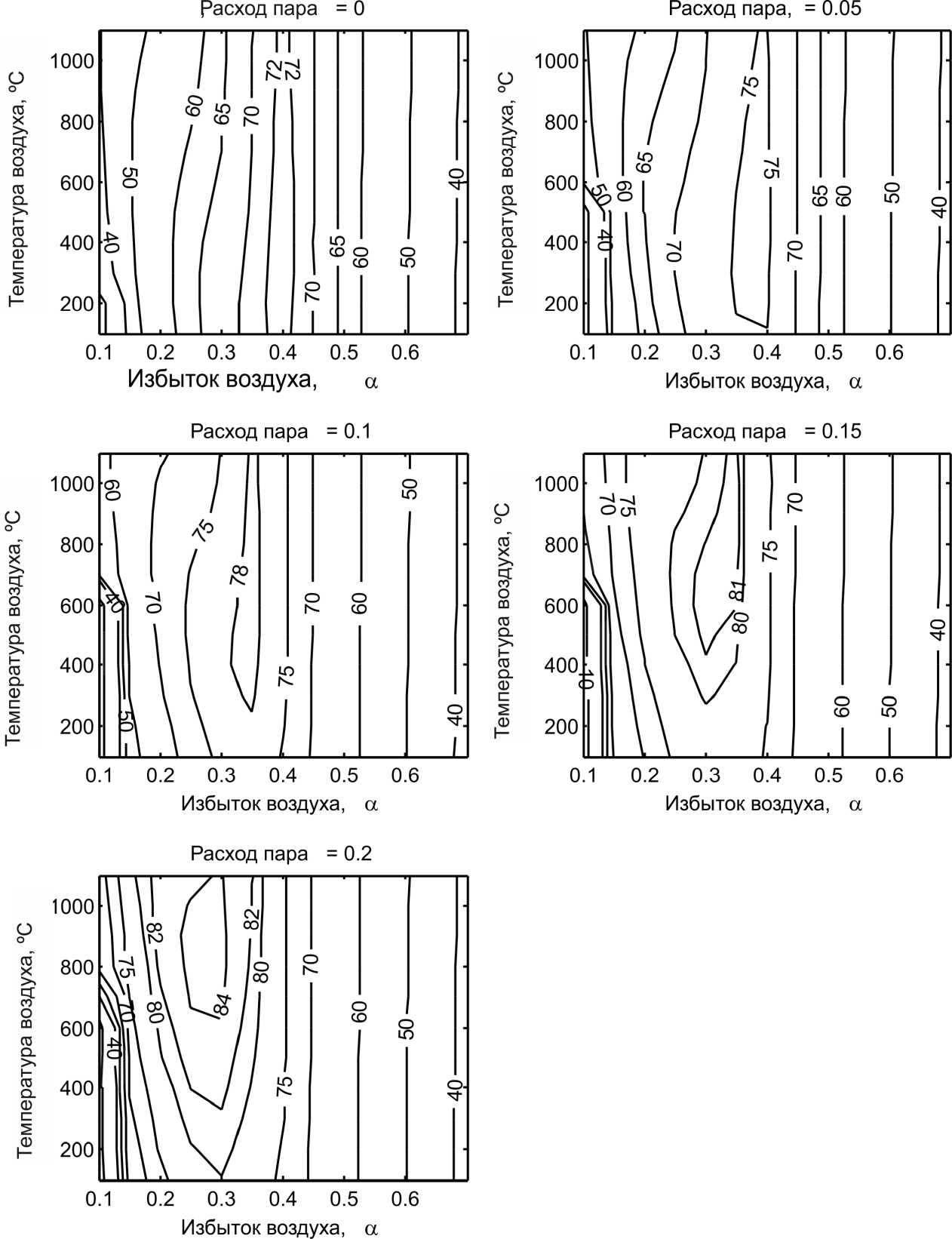
Рис. 1. Зависимость химического КПД (%) от коэффициента избытка воздуха, начальной температуры воздуха и удельного расхода пара

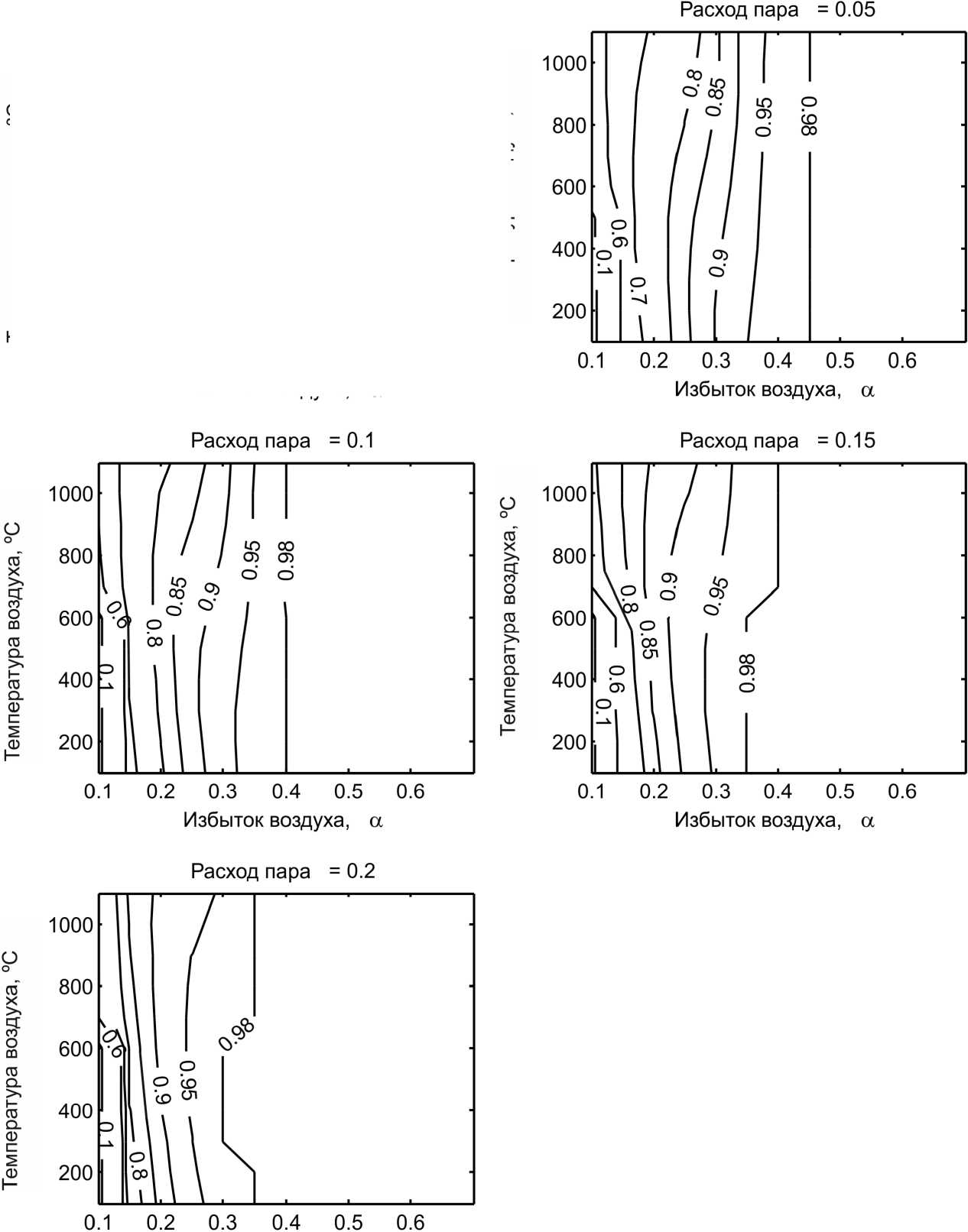
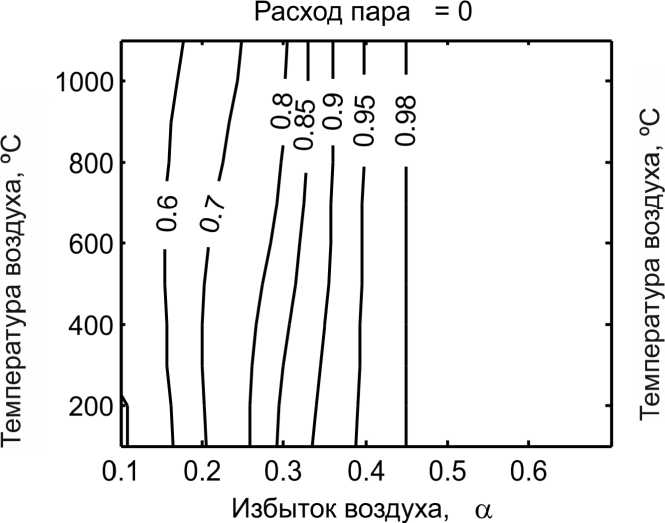
Избыток воздуха, а

Рис. 2. Зависимость степени конверсии топлива от коэффициента избытка воздуха, начальной температуры воздуха и удельного расхода пара

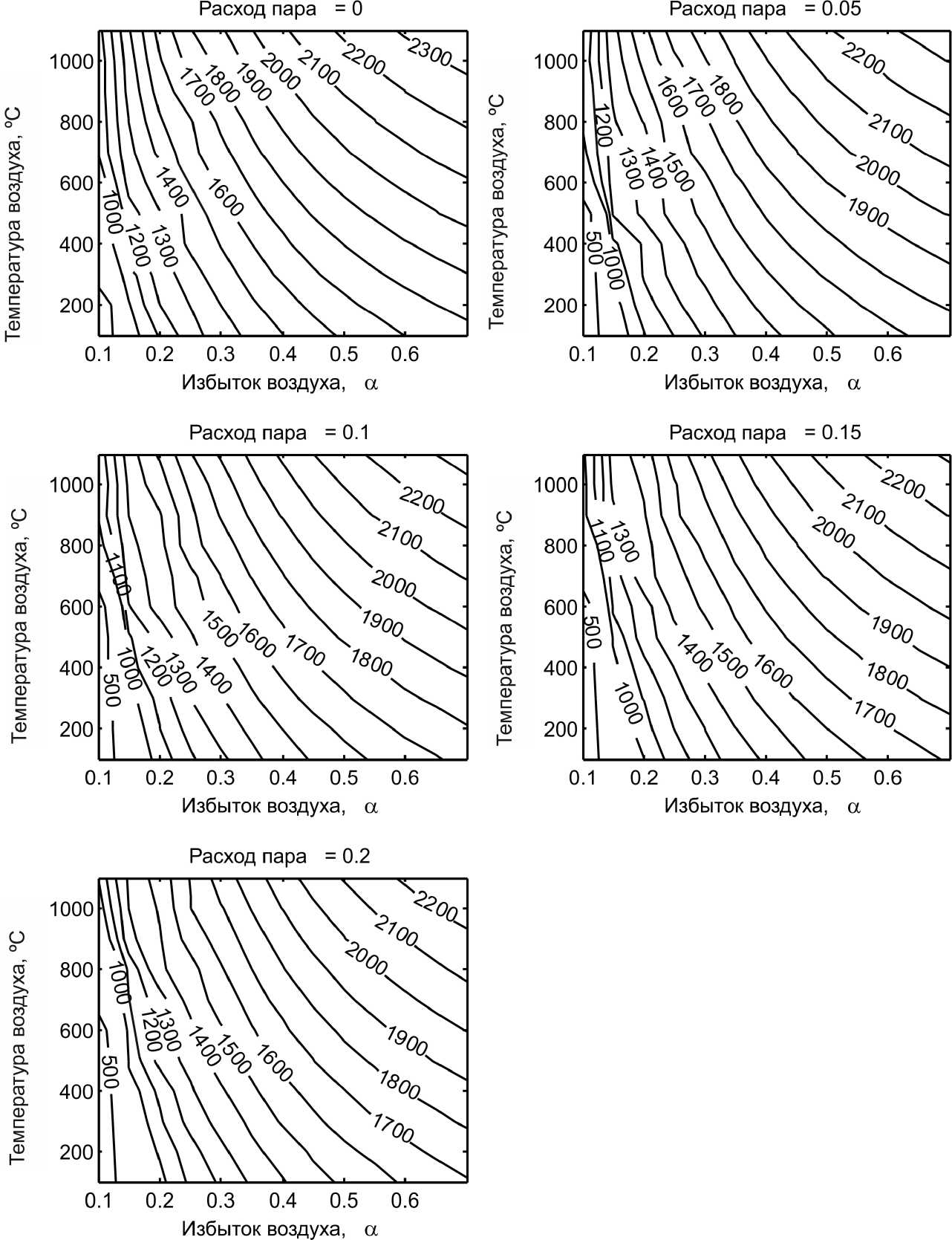
Рис. 3. Зависимость максимальной температуры факела (°С) от коэффициента избытка воздуха, начальной температуры воздуха и удельного расхода пара

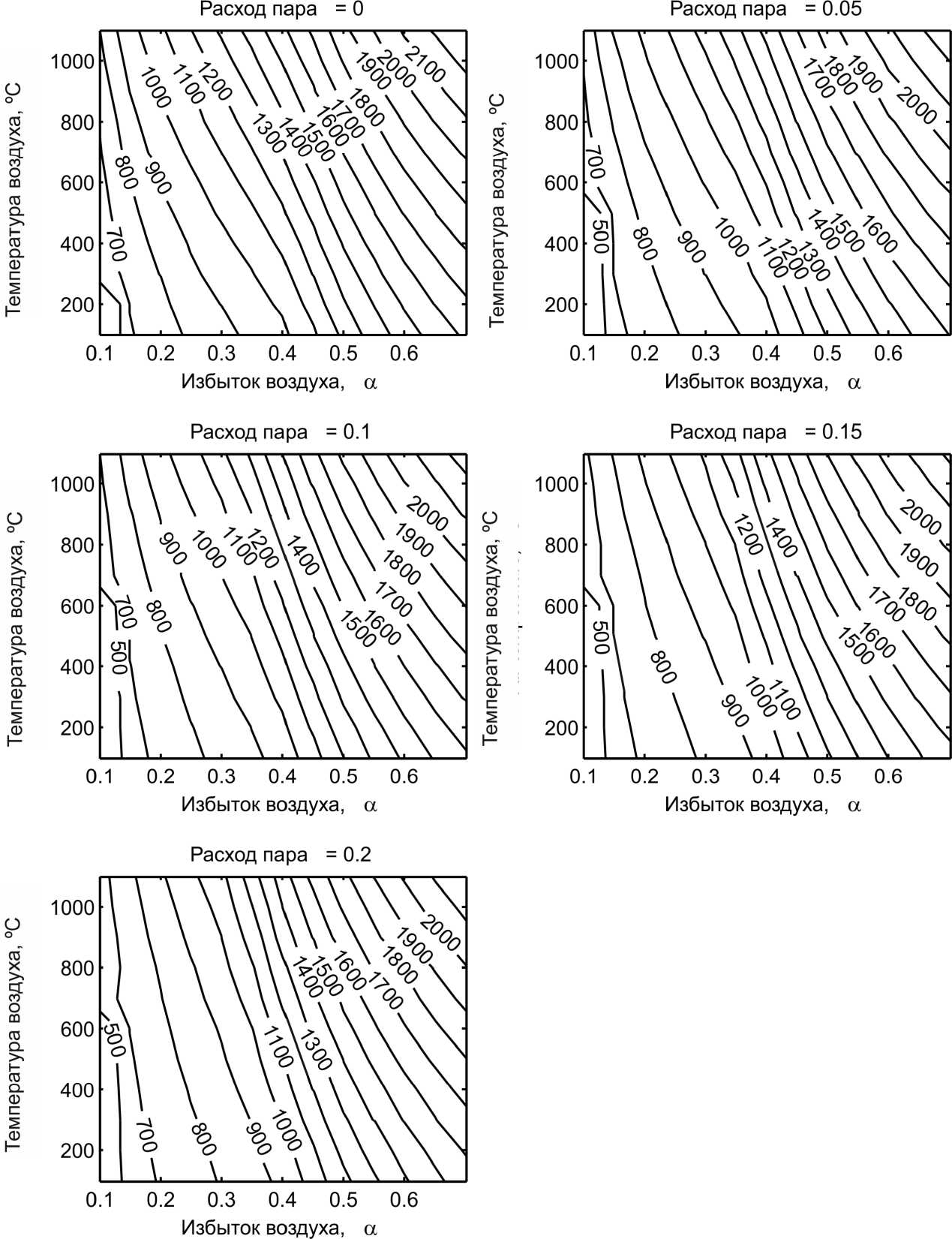
Рис. 4. Зависимость температуры выходящего из реактора газа (°С) от коэффициента избытка воздуха, начальной температуры воздуха и удельного расхода пара

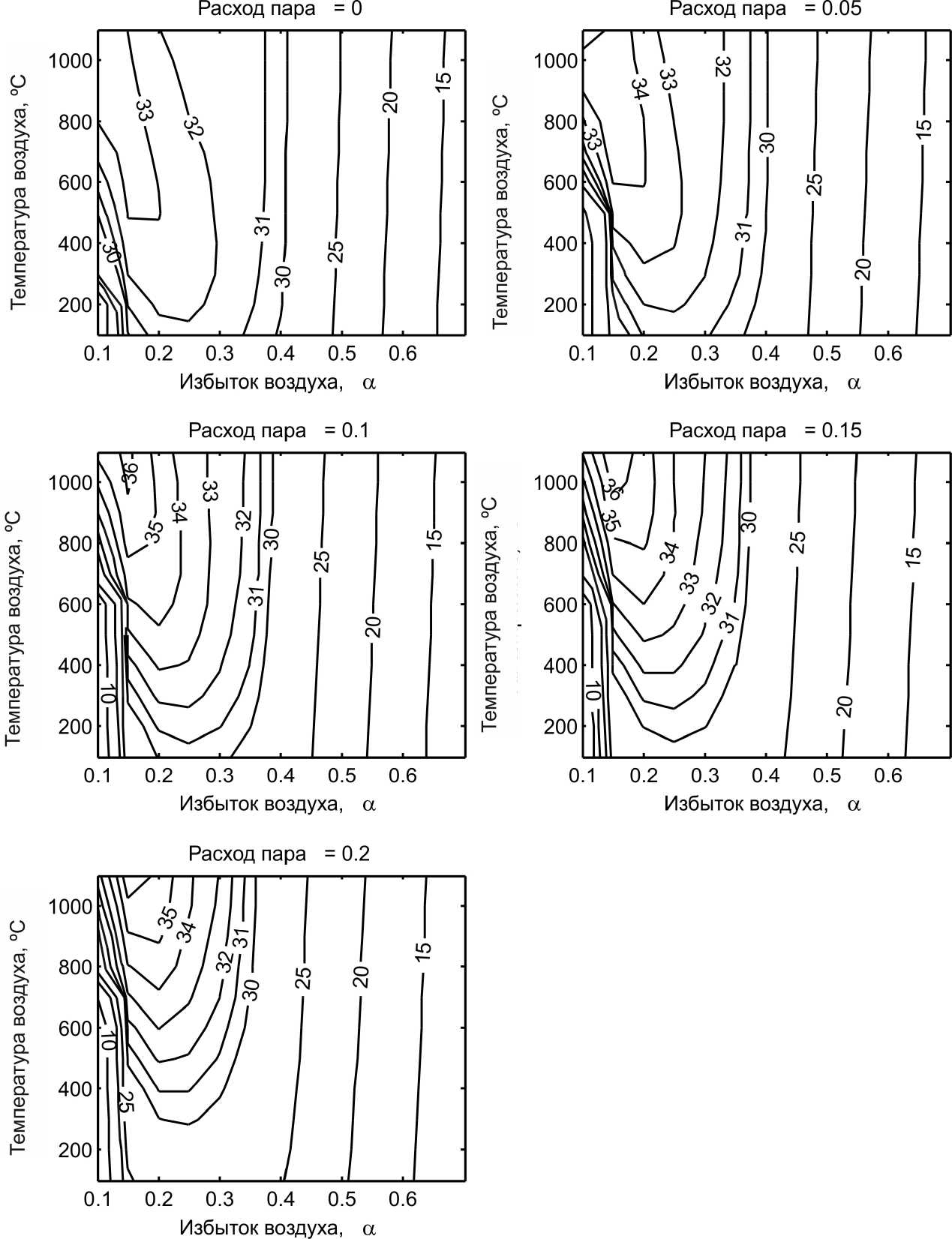
Рис. 5. Зависимость концентрации СО (% об.) в выходящем газе от коэффициента избытка воздуха, начальной температуры воздуха и удельного расхода пара

Расход пара = О

Расход пара = 0.05

ФсР

Избыток воздуха, ос

Расход пара =0.1

0.2   0.3   0.4   0.5   0.6

Избыток воздуха, ос

Расход пара =0.15

ГО о

ОО О

0.2   0.3   0.4   0.5   0.6

Избыток воздуха, ос

0.2   0.3   0.4   0.5   0.6

Избыток воздуха, ос

Расход пара = 0.2

Избыток воздуха, ос

Рис. 6. Зависимость концентрации Н2 (% об.) в выходящем газе от коэффициента избытка воздуха, начальной температуры воздуха и удельного расхода пара

Диаграммы зависимости конечной температуры газа от условий газификации (см. рис. 4) позволяют выбрать режим газификации под требования систем охлаждения и очистки газа [23]. Как уже указывалось выше, повышение начальной температуры позволяет повысить эффективность газификации. При этом снижается оптимальное значение избытка окислителя, а также за счет уменьшения плотности газа меняется средняя скорость движения газа. Поэтому при высоких температурах дутья эффективность процесса начинает падать, в том числе и из-за уменьшения времени пребывания частицы в реакторе. Поэтому длина реактора должна, вообще говоря, выступать в качестве одного из переменных параметров.

Выводы

В работе проведено численное исследование процесса газификации угольной пыли в потоке нагретого паровоздушного дутья. Для этого была выделена сетка управляющих параметров (начальная температура воздуха, коэффициент избытка окислителя), в которой были построены зависимости основных характеристик процесса газификации: химический КПД, температура, состав газа. Расчеты показывают возможность достижения химического КПД процесса газификации до 84 % при расходе пара 0,2 моль/моль углерода топлива при подогреве воздуха до температур порядка 800 °С.

Работа выполнялась при поддержке РФФИ (проект № 16-08-00739)