Численное исследование собственных колебаний слоистых усеченных конических оболочек, заполненных жидкостью

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2025PNRPU MECHANICS BULLETIN

Тонкостенные конические оболочки находят широкое применение в различных индустриальных приложениях в виде основных или вспомогательных элементов сложных конструкций. Определение их собственных частот и форм колебаний представляет определенный практический интерес и является неотъемлемой частью процесса проектирования. В отличие от цилиндрических оболочек, исследование конических осложнено следующим. Изменение кривизны приводит к разрешающим дифференциальным уравнениям с переменными коэффициентами, которые затрудняют получение аналитического решения [1]. В случае взаимодействия с идеальной жидкой средой ее моделирование также осложнено невозможностью получения аналитического решения для давления (потенциалов скорости или перемещения). Все эти ограничения вынуждают исследователей использовать как всевозможные полуаналитические подходы, включая непосредственное интегрирование дифференциальных уравнений, так и методы, основанные на численной дискретизации [2]. С применением данных численных инструментов за последние десятилетия проанализированы оболочки, выполненные из различных материалов, в том числе находящиеся под действием статических или динамических нагрузок [3–5]. Особый интерес представляют слоистые композиционные материалы, которые за счет схем укладки и углов армирования позволяют подобрать частотный спектр, обеспечивающий безопасное функционирование изделия с учетом ограничений на его габариты и массу. Ниже представлен обзор работ, посвященных собственным колебаниям пустых и содержащих жидкость слоистых конических оболочек (CКО).

Универсальная численная процедура на основе классической теории оболочек (КТО) и методе конечных элементов (МКЭ) предложена в работе [6] для анализа собственных и вынужденных колебаний произвольно армированных многослойных тонкостенных оболочек вращения. В качестве демонстрации возможностей алгоритма изучено влияние угла конусности на частоты колебаний трехслойной конической оболочки с различными граничными условиями. В статье [7] этот алгоритм был модифицирован с целью учета взаимного влияния симметричных и антисимметричных мод колебаний. Возникающее при этом различие в частотах продемонстрировано на перекрестно армированных свободно опертых и жестко закрепленных конических оболочках. Аналогичные исследования для толстостенных оболочек, выполненные с помощью МКЭ на основе уравнений неклассической теории оболочек (НТО) типа Тимошенко с учетом деформаций поперечного сдвига, приведены в работах [8; 9]. Влияние деформаций поперечного сдвига на примере многослойных поперечно армированных СКО с углом конусности 20° при различных комбинациях граничных условий оценено в [10]. Влияние изменения толщины на собственные частоты колебаний поперечно армированных CКО, описываемых в рамках КТО, изучено в [11] с помощью МКЭ. В работах [12; 13] на примере антисимметричных поперечно армированных CКО, описываемых в рамках КТО или НТО (first-order shear deformation theory, FSDT; далее под НТО понимается именно эта теория, если не оговорено другое), изучено влияние смешанных (мембранно-изгиб-ных) компонент жесткости на частотный спектр жестко закрепленных и свободно опертых оболочек. Эти решения, полученные с помощью метода степенных рядов, использовались в дальнейшем многими авторами для верификации своих результатов. Эффективный алгоритм численного решения задач о свободных колебаниях CКО, объединяющий в себе метод Галеркина для систем интегральных уравнений Фредгольма второго рода с обобщенной формой метода инвариантного погружения, представлен в [14]. На примере двухслойных антисимметричных поперечно армированных жестко закрепленных оболочек выполнено сравнение результатов, полученных на основе классических и неклассических теорий оболочек. Метод обобщенных дифференциальных квадратур (ОДК) применен в работах [15; 16] для анализа собственных колебаний антисимметричных поперечно армированных оболочек с различными граничными условиями, описываемых в рамках КТО и НТО соответственно. В последней из этих двух работ угол намотки являлся функцией угла конусности. Вариант метода ОДК, в котором производные в окружном и меридиональном направлениях аппроксимируются различными способами, предложен в [17]. С его помощью в рамках НТО выполнен анализ антисимметричных перекрестно армированных оболочек. Трехмерные соотношения линейной теории упругости используются в [18] для моделирования свободно опертых поперечно армированных CКО. С помощью асимптотического разложения по малому параметру и метода многих масштабов получена система дифференциальных уравнений, для решения которой использован метод ОДК. Определение оптимального угла намотки, обеспечивающего максимальное значение низшей частоты, в случае ненагруженной и нагруженной осевыми силами перекрестно армированной CКО при различных комбинациях граничных условиях осуществлено в [19; 20] с помощью методов последовательного линейного программирования и золотого сечения соответственно. Вычисление собственных частот колебаний произведено в конечно-элементном пакете ABAQUS с учетом деформаций поперечного сдвига. Универсальный подход, основанный на модифицированном вариационном принципе в сочетании с технологией многосегментного разделения, предложен в [21]. Он позволил проанализировать цилиндрические и конические слоистые оболочки с учетом деформаций поперечного сдвига, для которых заданы как классические, так и неклассические граничные условия. Более простая реализация этого метода на основе КТО позднее была использована в [22] при анализе поперечно армированных оболочек, расположенных на двухпараметрическом упругом основании. Упругое основание также принимается во внимание в работе [23]. Здесь в рамках теории оболочек Доннела с использованием метода Галеркина изучены собственные частоты симметричных поперечно армированных оболочек с различным количеством слоев и способами укладки. С помощью метода дискретных сингулярных сверток в работах [24–27] в рамках КТО и НТО исследованы свободные колебания поперечно армированных оболочек с различными граничными условиями. Анализ чувствительности вибрационного отклика симметричных двуслойных поперечно и перекрестно армированных CКО к случайному изменению свойств однонаправленного композиционного материала проведен в [28] посредством совместного использования МКЭ и метода возмущений. Дискретизация уравнений НТО осуществлена в работе [29] вейвлетами Хаара. Здесь представлены результаты анализа некоторых геометрических параметров и свойств материала на частоты колебаний поперечно и перекрестно армированных CКО. Аналогичный подход используется в [30] для анализа слоистых тел вращения переменной толщины, в том числе конических. Вариационный подход, основанный на КТО и комбинации методов Релея – Ритца, дифференциальных квадратур и рядов Тейлора предложен в [31] для исследования свободных колебаний CКО. Достоверность получаемых результатов оценена на примере антисимметричных поперечно армированных оболочек. Метод Релея – Ритца совместно с НТО и модифицированных рядов Фурье используется в [32; 33] для анализа колебаний слоистых конструкций, представляющих собой тела вращения. Авторами проведена оценка достоверности и рассмотрены CКО с различными углами конусности и граничными условиями. Колебания двух соединенных между собой поперечно армированных CКО изучены с использованием метода степенных рядов в работах [34] и [35] в рамках теории оболочек Доннела и НТО соответственно. Простой аналитический метод решения для слоистых оболочек с произвольным армированием, в том числе конических, основанный на анализе в пространстве состояний и решении в рядах в окружном направлении, предложен в [36]. В данной работе используется линейная теория оболочек Доннела и учитывается связь симметричных и антисимметричных мод. В рамках модифицированной версии НТО свободные колебания поперечно армированных оболочек при различных углах конусности, количестве слоев и схемах укладки проанализированы в [37] с помощью метода Га-леркина. Собственные колебания конических оболочек типа сэндвич, в которых лицевые поверхности представляют собой слоистый материал, изучены в [38] в рамках НТО с использованием ОДК. В работах [39–46] исследованы собственные колебания поперечно и перекрестно армированных CКО постоянной или переменной толщины при разных вариантах граничных условий. Для аппроксимации перемещений и углов поворота в случае использования НТО применяются сплайны Бикли третьего порядка. Анализируются композиционные материалы различного вида с симметричной и антисимметричной схемой укладки, разным количеством слоев и углами конусности. Детальное исследование влияния угла намотки, различных вариантов армирования и укладки на частоты колебаний CКО при произвольных комбинациях граничных условий приведено в работах [47; 48]. В обеих публикациях для построения разрешающей системы дифференциальных уравнений использована НТО. В [47] решение осуществляется с помощью рядов Уолша, а в [48] в схемах с бессеточной аппроксимацией применяется метод сглаживания локального градиента. Еще один универсальный способ определения частотного спектра слоистых конструкций, основанный на методе степенных рядов, предложен в [49]. Исследование различных параметров и граничных условий выполнено в рамках НТО для поперечно армированных CКО.

Из представленного обзора следует, что влияние различных параметров на свободные колебания пустых CКО достаточно хорошо изучено. Отметим, что во всех процитированных публикациях рассматриваются перевернутые конические оболочки. У таких конструкций радиус нижнего (левого) края меньше верхнего (правого). Данный факт имеет существенное значение в случае несимметричных граничных условий, например, консольного закрепления.

В меньшей степени исследованы CКО, взаимодействующие с жидкостью. Метод динамической жесткости использован в [50] для анализа свободных колебаний пятислойных поперечно армированных оболочек, погруженных в жидкость, а также заполненных ею частично или полностью. Вся конструкция разбивается по длине на ряд цилиндрических сегментов с постоянным радиусом, описываемых в рамках теории Рейснера – Нагди. В каждом из них гидродинамическое давление вычисляется по аналитической формуле с использованием функций Бесселя. Для изучения расположенных на упругом основании полностью заполненных жидкостью двуслойных и четырехслойных поперечно армированных оболочек с различными граничными условиями в работе [51] использованы НТО, балочные функции и метод Галер-кина. Вычисление гидродинамического давления осуществлено с помощью подхода, предложенного в [52]. Это позволило получить из волнового уравнения аналитическое выражение для потенциала скорости как функции угла при вершине и окружной гармоники.

Представленный обзор позволяет заключить, что в литературе отсутствует детальный анализ влияния угла армирования на собственные частоты колебаний полностью заполненной жидкостью конической оболочки при различных углах конусности и граничных условиях. Такое ограниченное количество исследований обусловлено невозможностью получения точного аналитического выражения для гидродинамического давления жидкости в случае конической оболочки. В настоящей работе для решения этой проблемы используется комбинация методов ортогональной прогонки (МОПГ), предложенной С.К. Годуновым [53], и метода ОДК [54]. Данный подход применялся ранее авторами для анализа изотропных конических, изотропных и слоистых цилиндрических оболочек, полностью или частично заполненных жидкостью [55–58], и показал хорошую точность при высокой вычислительной эффективности.

Постановка задачи

Рассматривается прямая, вертикально ориентированная усеченная коническая оболочка вращения (рис. 1) длиной L , радиусами R 1 and R 2 , углом при вершине A и толщиной h , полностью заполненная идеальной сжимаемой жидкостью объемом V f . Конструкция изготовлена из однонаправленного материала, слои которого ориентированы под углами +в и -в относительно меридиональной координаты. Необходимо при различных углах конусности A проанализировать влияние угла армирования в на низшие частоты колебаний двухслойных ([ в / —в ]) и трехслойных ([ в /0 ° / —в ]) оболочек с разными условиями закрепления на краях.

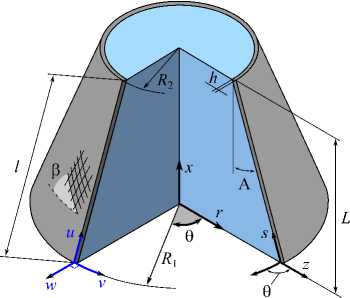
Рис. 1. Расчетная схема усеченной слоистой конической оболочки, заполненной жидкостью

Fig. 1. Computational scheme for the truncated layered conical shell with the fluid

Основные соотношения

Компоненты вектора деформации E _ij в криволинейной системе координат ( s , 0 , z ) для классической теории оболочек, основанной на гипотезах Кирхгофа – Лява, записываются в виде [59]

Е11 =е11 + z К11, Е22 =£22 + z к22, Е12 =£12 + 2 z к12, где

£ 11 = U + Г W ,   £ 22 = V + V U + Г 2 W ,

£12 = V' + U ’ —VV,  Kn = 0‘, k22 = 02 +V01, K12 = 01—V02 + r2 v',(1)

0 1 = - W '+ Г 1 U , 0 2 = - W ■ + r ₂ V ,

1 d(-)        .    1 3(-)

G-j =---—, G-0 =---—, V=

A1 Э s           A2 d0

Здесь: A ₁, A ₂ – коэффициенты Ламе; r ₁, r ₂ – кривизны; u , v, w – меридиональная, окружная и нормальная составляющие вектора перемещений оболочки; 0 1 , 0 2 -углы поворота недеформируемой нормали.

Физические соотношения, устанавливающие связь между вектором усилий и моментов T и вектором обобщенных деформаций Е = { е 11 , е ₂₂, е ₁₂, К 11 , к ₂₂,2 к ₁₂ } T , в матричном виде записываются как

T = { T p T 22 , S , M 11 , M ₂₂, M ₁₂ } T = D e =

AB

где коэффициенты, входящие в матрицу жесткостей D , определяются по формулам

(aj, bj, Cj) = J (1, z, z2) 0j (p)dz, (i, J = 1,2,3), h а компоненты матрицы 0j (P) вычисляются известным способом [60] в результате изменения свойств однонаправленного материала при повороте системы координат на угол р.

Уравнения движения оболочки принимают вид

/             \       д ² и

T11 + ¥(T11 — T22 ) + S + r1 (Q11 — M12 ) — Ро7Г = °’ д t

S+2 2у(S + rM 12) + T22 + Г2 (Q22 + M12) - Р° д t

Q11 +VQ11 + Q22 - riTll - r2T22 -p0 7T + p = 0’ д t

M 11 + v ( M 11 - M 22 ) + M 1 ’ 2 - Q 11 = 0,

M ‘ + 2 v M, ₇ + M — Q^ = 0,

12            12       2222

где Qii — поперечные силы, p0 = pdz , р - плотность ii материала, p – гидродинамическое давление, действующее со стороны жидкости на поверхность оболочки.

Раскладывая все компоненты (1), (2) в ряды Фурье по окружной координате 0

X (s, 0) = £ X( s )cos( j 0), j=0

Y ( s , 0 ) = £ Y j ( s )sin( J 0 ),

J = 0

X = { и , w , 0 1 , E h, E 22 , K 11 , K 22 , T 1 , T 22 , M 11 , M 22 , Q u, p },

Y = {v, 02, E12, K12, S, M12, Q22}, сводим геометрические (1) и физические (2) соотношения, а также уравнения движения (3) к системе восьми обыкновенных дифференциальных уравнений первого порядка относительно новых неизвестных [59]

y 1 = T 1 , y 2 = S + 2 r 2 M 12 , y 3 = M 11 , y 4 = Q 11 + JM 12 , y 5 = u , y 6 = v , y 7 = w , y 8 =0 1 -

Здесь j – номер гармоники при разложении в ряд

Фурье, J = J / A2. С учетом этого и используя представление для движения в виде y (t) = y exp (irot), запишем искомую систему следующим образом y' = f (J, й, y),                     (4)

где f = J (2r2M12 - у2)— V (y1 - T22) -rу4 - ®2Р0у5’ f2 = JT22 — 2VУ2 — r2Q22 - ro p0y6’ f> = У4 — V(У3 - M22 )- 2 JM12’            (5)

f4 = r1 y1 - VУ4 + r2T22 - J (Q22 + 2VM12 )— p - ГО Р0y7 ’ f > = e11 - r1 У 7 ’   f i = e12 + VУ 6 + Jy 5 ’ f7 =- У 8 + r1 У5’ fi =K11-

Здесь й - характеристический показатель, i² = — 1. Входящие в выражения (5) величины вычисляются по следующим формулам

^M 12 = ^b 33 ^e 12 ^{+ 2} c 33 ^K 12 ’ ^Q 22 =- ^JM 22 ’

^K 11 = [ ^a11 ( ^У 3 - ^b12 ^e 22 - ^C 12 ^K 22 ) - ^b11 ( ^y 1 - ^a 12 ^ 22 ^{— b}12 ^K 22 ) ] /

/ ( a11 C11 - b11 ) ’ e11 = ( y1 a12e22 b11K11 b12 K22 )/a11 ’

^T22 = ^a 12 ^e 11 ⁺ a 22 ^ 22 ^{+ b}12 ^K 11 ^{+ b} 22 ^K 22 ’

• ^e 12 = ^[ У 2 - ² ( ^b 33 ^{+ 2} r 2 ^C !3 ) ^J ( r 2 У 5 ^— У 8 - V У 7 ) ] /

  / ^[ a 33 ^{+ 4 r} 2 ( ^b 33 ^{+ r} 2 ^C 33 ) ] ’

где

• ^e 22 = ^Jy 6 ^{+ r} 2 У 7 ⁺ V У 5 ’ ^K 22 = ^{J 0} 2 ⁺ V У 8 ’ ⁰ 2 = r 2 У 6 ⁺ l^y 7 ’ ^K 12 = ^r 2 ( ^e 12 ⁺ УУ 5 ) ^{— J} ( У 8 ⁺V У 7 ) ’

^M 22 = ^b 12 ^e 11 ^{+ b} 22 ^ 22 ^{+ C} 12 ^K 11 ^{+ C} 22 ^K 22 "

В случае конической оболочки акустическое волновое уравнение и соответствующие граничные условия записываются в сферической системе координат ( x , а , 0 ) [61]

V2 p Jpp + 2 ^ + дx2 x дx

1 ( 1 д ² p + 1 д p + д ² p ^ _ 1 д ² p x ² ^ sin² а д0 ² tg ада да ² ) c ² д t²

Здесь c – скорость звука в жидкости.

На смоченной поверхности ( а = А ), оси вращения оболочки ( а = 0), нижней ( x = 0) и верхней ( x = L ) поверхностях жидкости гидродинамическое давление p удовлетворяет следующим условиям:

Vp • n  =1— 1 а=А x да а=А д2 w =—Р f w ’ (7) Vp • n   = ~    1 а=0 дp да = 0’ а=0 (8) x = 0: |p = 0, x = L : |p = 0,         (9)

дx              дx где n - единичные внешние нормали к области жидкости Vf, рf - плотность жидкости. Условие (9) характеризует взаимодействие жидкости с недеформируемыми поверхностями.

Уравнение (6) сводится к системе обыкновенных дифференциальных уравнений методом обобщенных дифференциальных квадратур [54]. Разделим область жидкости на n равных углов ai и определим производные l-го порядка функции p(x, а) в любой точке ai как d p(x’ai’ = Еcik’P(x’ak),  i=1,n’ l=1,n-1, (10)

Sa       k =1

где весовые коэффициенты c k ’ вычисляются по известным рекуррентным формулам [54]. С учетом (10) и граничных условий (7)-(8) вместо (6) получим следующую систему обыкновенных дифференциальных уравнений [55]

dy7+2(n-1) _ dx ■ y8+2( n-1)’ dy8+2( n-1) = - Pn— (x) + dx          x2

j2

⁺ y 7 + 2( n - 1) ^(_~2 sin a _n - 1

р П - ’1 ⁽ x )    x Ю ,    .-   ² y 8 + 2( n - 1)

1’ x-- tg an-1     c               x где y7+2(n-1) = Pn-1(x) и n-1

рП¹^ ^x ) = c n -n P 1^{( x} ) ⁺ Е c n ¹⁾1 k y 7+2( k -1) ⁺ c n - n P n ^{( x} )’ k =2

n -1

P^^ x ) = СПл1 P1(x ) + Е cn-1 ky 7+2( k-1) + c/' nPn (x )’ k=2

n -1                               n -1                             Z]²

c- ЕckPk(x) / ci’- Еcnk’Pk(x)- xрf o M =___k=2______________k=2______________Ot_

Pn (x’                   Л1’ -Л1М1’ /-(1’ cnn cn 1 cn 1 1 c11

,

Е ^c 1 ⁽ k’ Pk ⁽ x ’ ⁺ c n ’ P n ⁽ x ’

P 1^{( x} ’ = ^- —--------------

Совокупное число неизвестных, определяемых системами уравнений (4) и (11), составляет m = 8 + 2( n - 1).

Метод решения

Объединенная система уравнений (4), (11) c соответствующими однородными граничными условиями, задаваемыми на краях оболочки и столба жидкости yils=0 8i + yi+4|s=0 (1 -8i) = 0, i = 1...4,(12)

yL=L 8+4 + y+4 Is=L (1 < 4 ) = 0, i = 1.4,(13)

yilx=0 = 0, i = 10,12.m/2,(14)

y_\x=L = 0, i = 10,12.m/2,(15)

решается методом ортогональной прогонки Годунова [53] с численным интегрированием дифференциальных уравнений методом Рунге - Кутты четвертого порядка точности. В уравнениях (12)-(13), 8 i = 0, если заданы кинематические, и 8 i = 1, если заданы статические граничные условия.

Общее решение систем представляется в виде

Em/2 k=1 Ck y k ’ где Ck - некоторые константы и yj - совокупность линейно независимых решений объединенных систем, удовлетворяющих граничным условиям (12), (14). После интегрирования по заданному интервалу и удовлетворения граничных условий (13), (15) для определения постоянных Ck получим следующую алгебраическую систему

Е m =2 C k f k = 0, i = 1, m '.           (16)

Искомая задача сводится к вычислению таких значений го , при которых существует нетривиальное решение системы (16). Необходимым условием этого является равенство нулю определителя матрицы | f i_k ( го)| = 0 . Значения го , при которых происходит смена знака определителя | f i_k ( го)| , вычисляются с использованием шаговой процедуры и уточняются в полученном диапазоне методом Мюллера [62; 63].

Численные результаты

В численных примерах рассматриваются свободно опертые ( v = w = 7 i = M 11 = 0, SS), жестко защемленные ( u = v = w =0 1 = 0, CC) на обоих краях или консольно закрепленные ( 7 11 = 0, S + 2 r₂M ₁₂ = 0, M 11 = 0, Q 11 + jM ₁₂ = 0, CF) слоистые конические оболочки ( L = 0,9144 м, R_m = 0,876 м, h = 0,0015 м, v = 0,3), полностью заполненные сжимаемой жидкостью ( р f = 1000 кг/м³, c = 1500 м/с). При варьировании геометрических параметров длина оболочки L и средний радиус R_m = 0,5( R 1 + R 2 ) остаются неизменными при различных углах конусности. Их предельные значения подчиняются условию tg A < 2 R_m / L и соответствуют размерам эквивалентной по объему цилиндрической оболочки. Конструкция изготовлена из бор-эпоксидной смолы (AVCO 5505), физикомеханические характеристики для которой взяты из работы [6]. Для представления результатов расчетов вводятся безразмерные частоты колебаний Q и относительное изменение низшей собственной частоты колебаний ГО ( А , в ) как функции от угла конусности А и угла армирования в

Q = го L V р Rm/a _n, ГО ( А , в ) = ^{ГО ( А : в}--ГО 0^ • 100 % .

ГО(А, в)

Верификация результатов, получаемых с помощью описанного алгоритма, осуществлена авторами ранее в работах [55–58]. В связи с отсутствием достоверных решений для полностью заполненных жидкостью слоистых конических оболочек вращения выполним сравнение с результатами решения в конечно-элементном пакете AN-SYS. При моделировании конструкции из многослойного материала используется 8-узловой 3D-элемент оболочки с квадратичной аппроксимацией перемещений и углов поворота и смешанной интерполяцией составляющих тензора деформаций, учитывающий деформации поперечного сдвига в рамках теории Рейсснера – Миндлина (SHELL281). Дискретизация области жидкости осуществляется 20-узловым конечным 3D-элементом с квадратичной аппроксимацией перемещений и акустического давления (FLUID220). Выбор трехмерной постановки обусловлен тем, что в пакете ANSYS учет многослойного материала конструкции невозможен для осесимметричных или полуаналитических вариантов МКЭ, основанных на разложении решения в ряд Фурье по окружной координате. В таблице приведено сравнение низших частот го (Гц) для шести окружных гармоник j = 4…9, вычисленных при различных углах конусности, для перевернутой пятислойной ([90 ° /0 ⁰ /90 ⁰ /0 ° /90 ⁰ ]) оболочки, заполненной несжимаемой жидкостью ( L = 0,408 м, R m = 0,1355 м, h = 0,008 м, ν = 0,3, модули Юнга E 1 = 147 ГПа и E 2 = 9,8 ГПа, модуль сдвига G 12 = 5,09 ГПа, р = 1300 кг/м³).

Из представленных данных следует, что хорошее соответствие между различными методами решения имеет место только для однослойной оболочки. Отличия в результатах, растущие с повышением угла конусности A, могут быть объяснены как различными теориями, используемыми для описания тонкостенных тел, так и тем, что при трехмерной конечно-элементной реализации естественным образом учитывается взаимовлияние симметричных и антисимметричных мод колебаний, которое не может быть принято во внимание в осесимметричной постановке в случае неполных рядов Фурье. Для изотропных оболочек в случае применения в ANSYS полуаналитического варианта МКЭ такие различия отсутствуют [58].

По данным [56; 64; 65] известно, что в случае слоистой оболочки как пустой, так и содержащей жидкость, угол намотки оказывает влияние не только на низшую частоту колебаний, но и на соответствующую ей окружную моду. В существующих исследованиях эволюция собственной частоты и окружной гармоники строится только при варьировании одного параметра (угол армирования, уровень жидкости). В настоящей работе, наряду с аналогичными зависимостями, будут формироваться и двухпараметрические. Это позволяет провести более детальный анализ влияния различных параметров на частотный спектр.

На рис. 2–3 показаны зависимости низшей безразмерной частоты Q от угла армирования в, полученные для двуслойных и трехслойных пустых и заполненных жидкостью оболочек при различных комбинациях граничных условий и углах конусности A = 0°, 15°, 30°, 45°, 60°. На кривых маркерами обозначены места смены низших окружных форм колебаний (гармоник, которым соответствует низшая собственная частота) при одной полуволне в меридиональном направлении. У анализируемых пустых конических оболочек (см. рис. 2) волновое число для низшей моды не зависит от количества ограничений на краях конструкции и схемы укладки (j = 4), и уменьшается с ростом угла при вершине.

Сравнение низших частот колебаний го (Гц), полученных для перевернутой конической оболочки при различных углах конусности А

Comparison of the lowest vibration frequencies го (Hz) obtained for an inverted conical shell at different cone angles А

Угол А	Источник данных	Номер га			рмоники j
		4	5	6	7	8	9
Граничные условия CF
0 °	ANSYS	57,8	91,3	141,8	207,9	289,7	388,0
	Расчет	57,9	91,5	142,2	208,6	291,0	390,3
10 °	ANSYS	39,6	62,1	93,4	133,0	181,4	239,1
	Расчет	40,5	63,3	95,1	135,5	185,0	244,2
20 °	ANSYS	28,1	43,9	64,5	90,1	121,1	157,9
	Расчет	29,7	46,1	67,7	94,6	127,2	166,0
30 °	ANSYS	20,8	32,4	47,0	64,8	86,4	111,8
	Расчет	23,0	35,5	51,3	70,7	94,1	121,7
Граничные условия CC
0 °	ANSYS	108,7	121,1	158,2	217,3	295,6	392,1
	Расчет	108,8	121,2	158,6	218,0	296,9	394,3
10 °	ANSYS	107,3	120,1	151,3	194,0	246,5	309,1
	Расчет	108,9	121,4	152,5	195,4	248,3	311,5
20 °	ANSYS	104,2	115,6	136,5	164,5	199,3	241,1
	Расчет	109,2	120,0	140,9	169,0	204,2	246,6
30 °	ANSYS	99,6	106,6	120,2	139,4	163,9	193,7
	Расчет	108,3	114,5	127,9	147,3	172,3	202,9

Наличие жидкости внутри оболочки приводит к снижению не только частотного спектра, но и низших волновых чисел, в том числе и скачкообразному (см. рис. 3). В частности, для симметричных граничных условий (CC и SS) низшая частота для любой схемы укладки соответствует балочной моде колебаний (j = 1), которая в случае однонаправленного материала (в = 0°) остается неизменной фактически на всем диапазоне варьирования угла конусности. Как было отмечено выше и подтверждается данными, представленными на рис. 2–3, рост угла армирования приводит к изменению низшей окружной моды. При этом для некоторых конфигураций возможно ее повышение при небольших значениях угла намотки с последующим постепенным снижением. Несмотря на то что при углах в = 0° и в = 90° низшие частоты достаточно близки друг к другу, они не всегда соответствуют одинаковым окружным модам. Последовательности изменений минимальных гармоник от в = 0° до в = 90° могут быть достаточно близки для двуслойного и трехслойного пакетов или даже совпадать. Однако углы армирования, при которых осуществляются переходы от одной формы к другой, различаются.

Из представленных данных следует, что наличие жидкости и рост угла конусности Α приводят к снижению низшей частоты колебаний. В обоих случаях это связано с присоединенной массой жидкости. В первом из них эта связь является непосредственной, а во втором она обусловлена принятой зависимостью изменения геометрических размеров оболочки. При фиксированной высоте L с увеличением угла конусности растет длина образующей и, следовательно, площадь смоченной поверхности, на которую действует жидкость. Рост образующей повышает массу оболочки, снижает ее жесткостные свойства и низшую частоту. Данное заключение не относится к консольно закрепленным коническим оболочкам. При фиксированном среднем радиусе Rm увеличение угла при вершине A приводит к росту одного радиуса и уменьшению другого. Закрепление большего из них повышает жесткость системы и, следовательно, приводит к росту частоты до тех пор, пока эффекты на свободном крае не становятся доминирующими. Для конкретного угла конусности данный механизм обеспечивает существование оптимального диапазона углов намотки, на котором достигается максимальный рост частоты.

Повышение низшей частоты прямой консольной оболочки имеет место вплоть до определенного значения Α. Аналогичная особенность в поведении собственных частот в зависимости от угла конусности была выявлена ранее как для пустых, так и заполненных жидкостью перевернутых изотропных оболочек [66; 67]. Рост низшей частоты пустой, жестко закрепленной только по большему радиусу оболочки продемонстрирован в работе [68].

В отличие от угла конусности Α, изменение угла армирования β оказывает влияние на мембранную и изгиб-ную жесткости, наоборот, приводит к повышению низшей частоты Ω . Ее наибольшее значение для различных Α достигается при разных углах намотки. Причем для разных вариантов укладки и комбинаций граничных условий эти углы армирования, как и низшие окружные моды, остаются практически неизменными при малых и средних углах конусности, а с их ростом постепенно смещаются в область более высоких значений.

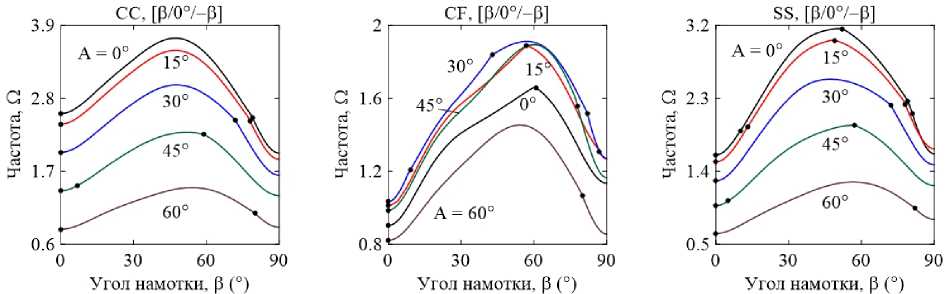
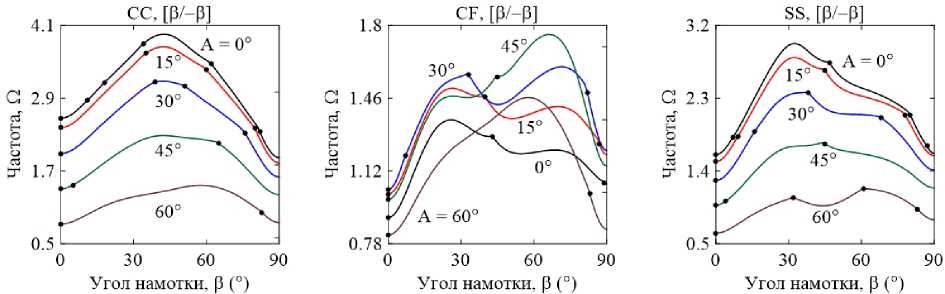
Рис. 2. Зависимости низших частот Ω от угла намотки β , полученные при различных углах конусности Α для прямых пустых трехслойных и двуслойных оболочек с разными комбинациями граничных условий

Fig. 2. Dependences of lowest frequencies Ω on the ply angle β obtained at different cone angles of straight empty three-layer and two-layer shells with different combinations of boundary conditions

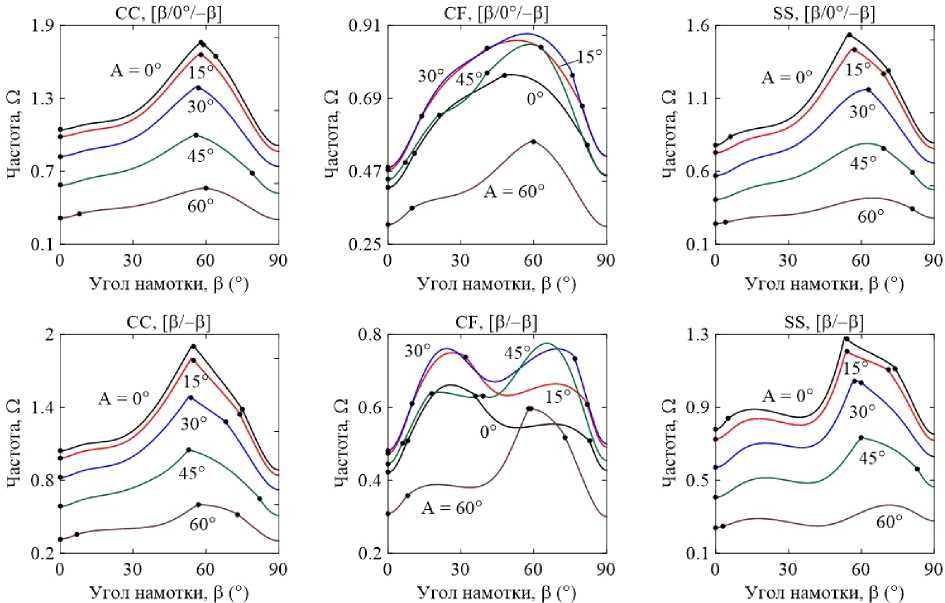
Рис. 3. Зависимости низших частот А от угла намотки в , полученные при различных углах конусности А для прямых трехслойных и двуслойных оболочек, полностью заполненных жидкостью, с разными комбинациями граничных условий

Fig. 3. Dependences of lowest frequencies fl on the ply angle в obtained at different cone angles of straight three-layer and two-layer shells filled with a fluid, with different combinations of boundary conditions

Содержащие жидкость оболочки с симметричными граничными условиями имеют ярко выраженный локальный максимум частоты. Диапазон углов армирования, обеспечивающих частоты, близкие к максимальному значению, расширяется с повышением угла при вершине. Для консольно закрепленных двуслойных оболочек существуют два угла намотки в , дающие близкие по величине значения частот. Особенно отчетливо это прослеживается в случае углов А = 30 ° и А = 45 ° .

На рис. 4–5 приведены изоповерхности относительного изменения низшей частоты колебаний ГО как функции углов армирования в и конусности A, полученные для двуслойных и трехслойных оболочек при различных комбинациях граничных условий. Маркерами обозначены места смены окружной формы колебаний j , соответствующей низшему значению частоты. В расчетах базовой точкой, относительно которой отслеживается изменение окружной моды, является координата (0,0). В данном случае это соответствует однослойной цилиндрической оболочке, которая либо не содержит жидкость, либо заполнена ею полностью. В зависимости от рассматриваемой конфигурации окружная мода в базовой точке изменяется.

Представленные графики демонстрируют упорядоченное изменение окружных гармоник, соответствующих низшей частоте, при разных комбинациях варьируемых параметров. Природа этой упорядоченности в большинстве случаев является труднообъяснимой и, очевидно, зависит от совокупности геометрических и физико-механических параметров, а также внешних условий. Например, отдельные частоты разных окружных гармоник более чувствительны к изменению параметров, что проявляется в их ускоренном росте или снижении по сравнению с другими. В частности, с увеличением угла намотки изменение низшей окружной моды, в некоторых случаях скачкообразное, происходит при смене тренда с повышения частоты на ее снижение.

Упорядоченные последовательности изменений номеров окружных гармоник j представляют собой чередование низших окружных мод, присущих системе при данной комбинации параметров. По этой причине при фиксированном угле конусности одной и той же окружной гармонике могут соответствовать разные низшие частоты в зависимости от угла армирования. При наличии жидкости эта особенность наиболее ярко выражена для трехслойных консольных оболочек (CF). Например, при угле конусности А = 42 ° окружное число полуволн j изменяется следующим образом: 3–2–3–1–3–2. При этом поведение низшей частоты колебаний с ростом угла армирования является немонотонным. Данные особенности могут быть использованы при проектировании элементов конструкций, когда за счет выбора схемы укладки и угла намотки для заданного угла конусности требуется обеспечить необходимую форму колебаний в определенном диапазоне частот.

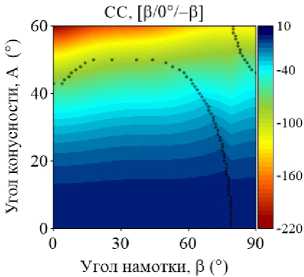
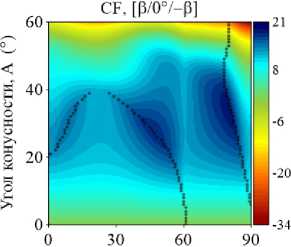
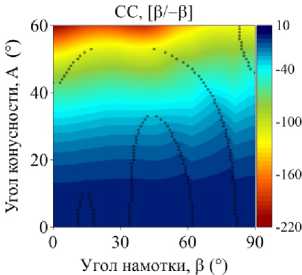
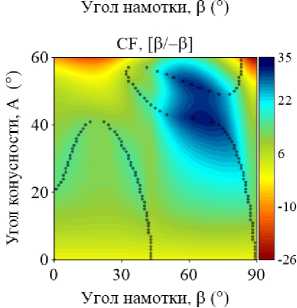
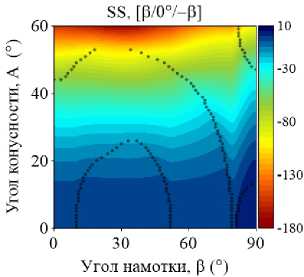
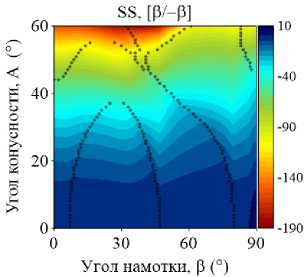
Рис. 4. Изоповерхности относительного изменения низшей частоты колебаний ω как функции углов конусности Α и армирования β , полученные для прямых пустых трехслойных и двуслойных конических оболочек при различных комбинациях граничных условий

Fig. 4. Isosurfaces of the relative variation of the lowest vibration frequency ω of three- and two- layer empty conical shells with different combinations of boundary conditions as a function of ply angle β and cone angle A

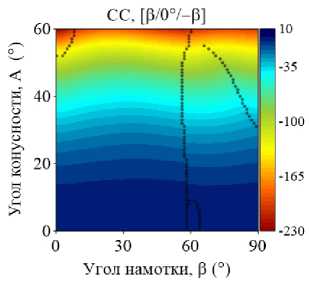
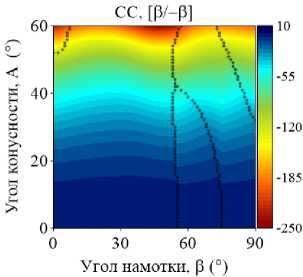
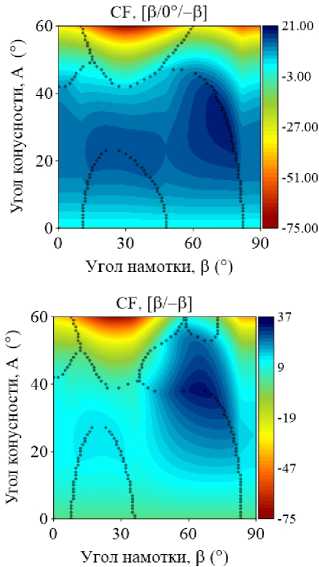
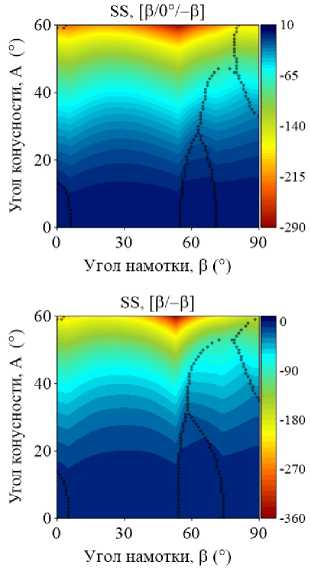
Рис. 5. Изоповерхности относительного изменения низшей частоты колебаний ω как функции углов конусности Α и армирования β , полученные для прямых двуслойных и трехслойных конических оболочек, полностью заполненных жидкостью, при различных комбинациях граничных условий

Fig. 5. Isosurfaces of the relative variation of the lowest vibration frequency ω of three- and two-layer conical shells filled with fluid with different combinations of boundary conditions as a function of ply angle β and cone angle A

Приведенные на рис. 4–5 изоповерхности, по сравнению с графиками, представленными на рис. 2–3, дают более полное представление о распределении частотного спектра. Они наглядно определяют область параметров, позволяющих обеспечить его повышение. Обобщая приведенные результаты, можно заключить, что только консольно закрепленная коническая оболочка гарантирует максимизацию фундаментальной частоты при широком диапазоне углов конусности и армирования по сравнению с эквивалентной цилиндрической оболочкой. В том случае, если эксплуатационные требования к конструкции налагают ограничения на фундаментальную частоту колебаний, применение слоистой цилиндрической оболочки является более предпочтительным для всех остальных граничных условий.

Заключение

Представлены результаты численного исследования собственных частот колебаний вертикальных композитных прямых усеченных конических оболочек, полнос- тью заполненных идеальной неподвижной жидкостью. Проанализировано влияние схемы укладки слоистого композита на низшие частоты колебаний оболочек с разными вариантами граничных условий на краях при различных значениях углов конусности и армирования. Выявлено, что для закрепленной у основания конической оболочки существуют комбинации параметров (углы армирования и конусности), при которых фундаментальные частоты колебаний оказываются выше значений эквивалентной слоистой цилиндрической оболочки. Установлено, что для оболочек с симметричными граничными условиями имеют место такие углы армирования, при которых максимальная низшая частота соответствует балочной моде колебаний. Продемонстрировано, что можно подобрать такие геометрические параметры и физико-механические характеристики слоистого композиционного материала, которые будут обеспечивать подходящий частотный спектр и форму колебаний. Это позволит избежать появления резонанса в опасном диапазоне частот и увеличить жизненный цикл конструкции, взаимодействующей с жидкостью.