Численное исследование термомеханического поведения кристаллизующейся полимерной среды с учетом больших деформаций
Автор: Куликов Р.Г., Куликова Т.Г., Сметанников О.Ю.
Статья в выпуске: 1, 2018 года.
Бесплатный доступ
Предложены феноменологические определяющие соотношения для кристаллизующейся полимерной среды, полученные в рамках нелинейной механики деформируемого твердого тела. Соотношения основаны на представлении среды в виде композиции расплавленного и полностью закристаллизованного материала с учетом истории непрерывного зарождения и деформирования новой фазы в интервале температур фазовых превращений. Выполнена общая постановка эволюционной краевой задачи нелинейной механики полимерных материалов в условиях протекания фазовых переходов с использованием предложенных определяющих соотношений. Рассмотрены алгоритмы численной реализации теплокинетической задачи и задачи определения напряженно-деформированного состояния затвердевающей системы для случая плоского деформированного состояния. Разработана процедура линеаризации, удобная с точки зрения построения численных алгоритмов решения поставленных эволюционных краевых задач, использующая предположение о близости каждой промежуточной конфигурации к текущей, что соответствует процедуре наложения на конечные деформации кристаллизующейся среды малых деформаций закристаллизовавшихся частиц. Процедура линеаризации исходной постановки задачи механики реализована с учетом температурных и структурных деформаций. Разработан и реализован численный алгоритм решения поставленной плоской краевой задачи с целью исследования особенностей эволюции напряженно-деформированного состояния в полимерной конструкции. Предложена и реализована методика построения дискретного аналога поставленных краевых задач, основанная на использовании процедуры метода Галеркина с выбором базисных функций с компактным носителем по методу конечных элементов. При этом в качестве узловых неизвестных приняты приращения функций перемещений на текущем временном шаге. Установлены закономерности формирования дефекта типа раковины в кристаллизующемся полимерном цилиндре.
Кристаллизация, полимер, большие деформации, определяющие соотношения, термомеханика, численный алгоритм, линеаризация, метод конечных элементов
Короткий адрес: https://sciup.org/146211712
IDR: 146211712 | УДК: 539.3 | DOI: 10.15593/perm.mech/2018.1.02
Текст научной статьи Численное исследование термомеханического поведения кристаллизующейся полимерной среды с учетом больших деформаций
ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2018PNRPU MECHANICS BULLETIN
Процесс производства значительной части полимерных изделий и конструкций содержит этап охлаждения материала, сопровождающийся его кристаллизацией. Технологические и остаточные напряжения, формирующиеся вследствие температурной и деформационной неоднородностей, могут приводить к снижению эксплуатационных качеств изделий и даже их разрушению еще на стадии изготовления. Поэтому актуальной является проблема описания термомеханических процессов в полимерных материалах в условиях фазового перехода. Модели поведения таких сред должны включать определяющие соотношения, единым образом описывающие связь тензоров напряжений и деформаций в широком интервале температур, включающем диапазон фазовых превращений. Для реальных процессов и изделий решение задач описания закономерностей формирования полей технологических напряжений возможно только численными методами. Поэтому важное значение приобретает построение удобного в реализации численного алгоритма решения краевой задачи термомеханики кристаллизующейся полимерной среды.
Хорошо известны модели поведения отверждающихся полимерных материалов, предложенные в разное время в работах [1–3]. Общая черта этих моделей – стремление получить возможность простой оценки остаточных напряжений. Ряд авторов при построении моделей термомеханического поведения для кристаллизующегося полимера предполагает упругое поведение материала и малость деформаций. Например, в работе [4], в рамках указанных предположений, с использованием феноменологического подхода разработана система определяющих уравнений, описывающих термомеханическое поведение аморфнокристаллических полимеров. В работах [5–9] моделирование термомеханического поведения полимера проведено с учетом больших деформаций. При этом многие из предлагаемых моделей поведения полимера основаны на упруговязкопластическом подходе [7–10], разработаны для конкретных полимерных материалов [5, 10] или определенных видов напряженно-деформированного состояния. Например, в работе [6] разработана модель описания механического поведения полимера в диапазоне температур, включающем процессы стеклования, для случаев одноосного нагружения и плоского напряженного состояния. В [8] рассматривается развитие упруговязкопластической теории для моделирования зависимости отклика аморфных полимеров от скорости деформирования и температуры с учетом больших деформаций.
В последнее время интерес к вопросам описания деформационного поведения полимеров при фазовых превращениях вызван все более широким использова- нием их в качестве материалов с памятью формы, поскольку в основном эффекты памяти формы в полимерах связаны с фазовыми или релаксационными переходами. Различным аспектам деформационного поведения полимеров, связанным с исследованием эффектов памяти формы, посвящено большое число публикаций [11– 15]. Большинство предлагаемых в них моделей используют гипотезу о малости деформаций и предназначены для описания поведения полимера в достаточно узком температурном диапазоне и моделирования конкретного механизма памяти формы и не могут описывать другие термомеханические эффекты.
В настоящей работе рассматривается построение феноменологических определяющих соотношения для кристаллизующегося полимера с учетом больших деформаций, непрерывным образом отражающих связь тензоров напряжений и деформаций в широком диапазоне изменения температур. Соотношения основаны на представлении среды в виде композиции расплавленного и полностью закристаллизованного материала с учетом истории непрерывного зарождения и деформирования новой фазы в интервале температур фазовых превращений. Также в работе рассматривается модельная задача о зарождении раковин в кристаллизующейся среде, демонстрирующая возможности применения предлагаемых определяющих соотношений.
-
1. Постановка краевой термомеханической задачи для кристаллизующегося полимера.
В предположении, что технологические напряжения не влияют на температуру и протекание процесса кристаллизации, возможно разделение задачи на две самостоятельные задачи:
-
1) теплокинетическая задача – задача по определению полей распределения температуры и степени кристаллизации;
-
2) краевая задача по определению напряженно-деформированного состояния (НДС) затвердевающей системы.
Интенсивное тепловыделение при кристаллизации и теплоотдача в окружающую среду, низкая теплопроводность полимерных материалов, зависимость процесса кристаллизации от температуры приводят в процессе изготовления изделий из полимеров к существенно неоднородным полям температуры и степени кристаллизации. Прогнозирование температурного и конверсионного полей в ходе процесса может быть осуществлено в рамках известной теплокинетической модели, согласно которой постановка задачи включает:
– нестационарное уравнение теплопроводности с переменными коэффициентами д T (x, Л с (T )Р( T)
д t
= div ( X ( T ) grad ( T ( x , t ) ) ) + p ( T ) Q , x e V ; (1)
– уравнение кинетики неизотермической кристаллизации [16, 17]
d a ( x , t ) dt
= K 1 exp
U 1
T
RT ( x , t ) T p - T ( x , t )
x ( 1 + A y a ( x , t ) ) ( a p ( T ) -a ( x , t ) ) , x e V ;
– начальные условия
X
a ( x ,0 ) = 0, T ( x ,0 ) = T y , x e V ; (3)
– граничные условия по температуре, где c - удельная теплоемкость; p - плотность материала; X - коэффициент теплопроводности; T - температура; t – время; x – радиус-вектор произвольной точки тела; Q = Qkda/dt - скорость выделения тепла в ходе протекания реакции кристаллизации; Qk – тепловой эффект реакции кристаллизации; a - степень кристаллизации материала, которая в ходе процесса принимает значения в пределах от нуля до некоторого предельного значения, зависящего от температуры и представляющего собой равновесную степень кристаллизации ap; R - универсальная газовая постоянная; Tp - температура плавления; K1, U1, у, A0 - макро-кинетические константы, определяемые экспериментально; V – область затвердевающего полимера.
Уравнения (1) и (2) образуют связанную систему уравнений и решаются совместно. Результатом решения теплокинетической задачи являются пространственновременные поля распределения температуры и степени кристаллизации, с учетом которых решается задача определения НДС изделия.
Для постановки краевой задачи относительно НДС затвердевающей системы необходимы физические соотношения, которые в силу специфики задачи непрерывным образом отражают связь тензоров напряжений и деформаций в широком диапазоне изменения температур. Эти соотношения были получены с учетом больших деформаций в рамках следующих гипотез и положений:
-
- кристаллизующаяся полимерная система в каждый момент времени в каждой точке системы рассматривается как смесь расплава полимера и полностью закристаллизовавшегося продукта, относительная доля которых в общем объеме характеризуется величиной степени кристаллизации a ( t ) ;
-
- материал в процессе превращения и дальнейшего деформирования остается макроизотропным;
-
- для описания механического поведения расплава полимера и закристаллизовавшегося полимера примем упругий закон.
Для описания поведения среды при конечных деформациях будем использовать понятия начальной (соответствующей моменту времени t 0 ) и текущей (соот-
ветствующей моменту времени t ) конфигураций [18]. Пусть начальная конфигурация определяется радиусом-вектором r = r ( q 1 , q 2 , q 3 ), а текущая конфигурация -радиусом-вектором R = R ( q 1, q 2, q 3 ), где q - обобщенные координаты.
Пусть в момент времени t 1 закристаллизовалась доля полимера, характеризуемая приращением степени кристаллизации Аа1 = Аа ( t1 ) . Градиент места из конфигурации, в которой появилась доля кристаллической фазы Аа 1, в текущую конфигурацию может быть записан следующим образом [18]:
F = F = f n ■ ... ■ f 2 ■ f i , (4)
где f i – градиент места из конфигурации, соответствующей моменту времени ti , в конфигурацию, соответствующую моменту времени t i + 1.
Для градиента места из конфигурации, соответствующей моменту времени t 2 и кристаллизации доли полимера, характеризуемой приращением степени кристаллизации Аа 2, в текущую конфигурацию справедливо следующее выражение:
l f „.F f 2 n ... 32 .
Рассмотрим п -й дискретный шаг по превращению Аа „ :
F =f nn .
Учитывая, что F 2 = F ■ f 1 - 1, F 3 = F 2 ■ f - 1,., F n = = F n -1 ■ f n - , выразим все градиенты места F через градиент места, связывающий начальную и текущую конфигурации:
F i = F ■ f t - 1, F 2 = F ■ f t - 1, , F „ = F ■ f t - 1, (5)
где f t - 1 - градиент места из начальной конфигурации в конфигурацию, соответствующую приращению степени кристаллизации Аа i .
Для получения определяющих соотношений необходимо записать выражение для упругого потенциала системы W [19], зависящего от тензора меры деформаций Коши-Грина. Упругий потенциал кристаллизующейся системы может быть представлен в виде суммы упругого потенциала для аморфной фазы и упругого потенциала для кристаллической фазы
W(G?) = (1 -а(t))Wa (G?) + W^ + W2 + ,„ + Wn, (6)
где Wip = Wkp (g^-1 )Ааi - доля потенциала, которую привносит в общий потенциал часть кристаллической фазы, соответствующая приращению степени кристал- лизации Ааi; Gt = FT ■ F - тензор меры деформаций Коши-Грина [19], соответствующий деформированию от начального до текущего момента времени; GT-1 = FiT ■ Fi = f, T ■ Gt ■ ft-1 - тензор меры деформаций Коши-Грина, соответствующий деформированию от момента времени ti до текущего момента времени.
После осуществления предельного перехода в соотношении (6) по степени кристаллизации выражение для упругого потенциала можно записать в виде
W(g;) = (1 -а(t))Wa (Gt) + + J)Wcp (f;T ■ Gt ■ f-)^а(т).
Используя в качестве упругого потенциала двухконстантный потенциал Пенга-Ландела [20], выражение связи тензора Пиолы-Кирхгофа второго рода P ˆ II с тензором меры деформаций Коши-Грина записываем следующим образом:
P n ( t ) = ^:
1/3
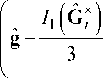
+
+ B a 1 3
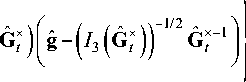
1/3
(1 -а ( t )) +
а ( t )
+ J
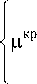
( I 3 ( G T t ) )
g -
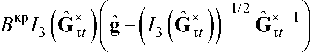
- d а ( т ),
где (J Tt = F T - T ■ (J t ■ F T - 1, pa, B a, цкр ,B кр - механические характеристики аморфной и закристаллизовавшейся части материала соответственно; I 1, I 3 – первый и третий главные инварианты тензора второго ранга; g ˆ – метрический тензор.
Вариационная постановка краевой квазистатиче-ской задачи термомеханики кристаллизующейся среды может быть получена с использованием процедуры Бубнова–Галеркина [20] и в случае отсутствия внешних силовых воздействий принимает вид
J P ii ■■5< C dV o = 0,
V 0
где C = ( G ; - 8 )/2 – тензор деформаций Коши-Грина;
V 0 – начальный объем тела.
К достоинствам рассматриваемой постановки стоит отнести то, что она сформулирована в исходной конфигурации, что существенно упрощает построение чис- ленного алгоритма расчета. При этом полагается нелинейность геометрических соотношений, обусловленная необходимостью учета больших деформаций. Сложность получения решения задачи в форме (9) обусловлена как нелинейностью постановки, так и проблемами, связанными с необходимостью учета возникающих температурных и структурных деформаций.
При решении модельной задачи будем полагать, что зарождение полости в материале происходит при достижении объемной деформации в окрестности рассматриваемой точки некоторого предельного значения. Для придания поведению рассматриваемого тела большей реалистичности предположим, что предельная величина деформации разрушения несколько варьируется по объему. Разрушение будем моделировать занижением в окрестности рассматриваемой точки модуля кристаллической фазы. С учетом неосесимметричного характера зарождения полостей решение механической задачи будет рассматриваться в декартовой системе координат для случая плоского деформированного состояния. В данном случае компоненты тензоров P ˆ II и C ˆ конкретизируются следующим образом:
C xy
(PII)„ = У 13
■ -I
11 (2 C„ +1)1
I 3
+
+ B a 1 3 1 - 1 ;'2
I 3
(1 -а( t))+
-___-
-
c xx
^_
+ K 13
-
1 1 ( 2 C yy
T t
+ B кр I 3 1 - I 3 - V 2
-
I 3
+
( 2 C„
T t
-
I 3
d а(т),
(PII )yy = ^13-V3| 1
1 1 ( 2 C xx + 1 ) Y
3 1 3 J
+ B a 1 3 I 1 - 1 -
Ц2 ( 2 C xx + 1 )
I 3
+
+Ккр 'I - 1'3 1
т (2 CxTtt
I 1 xx
I 3
+
+ B кр I3 1 - I - 12
2 C xx
T t
\ 1
■_.’
I 3
• d а ( т ) ,
( Pii ) xy = p 13-4/3J 2 Cxy + B a I3-V22 Cxy J (1 - а (t)) +
'_’
+ J цкр I -44 S C xyt + B кр I3 - 12 2C xyt d а ( т ) ,
d x 1 P U x Y d x 2 ( d x )
+ —
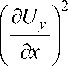
dUy 1 f 5Ux \ dy 2 ( dy )
+ -
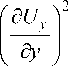
d ux + d Uy + d ux d ux + d Uy d Uy dy dx dx dy dx dy
где 1 1 = 2 ( C xx + C yy ) + 3, 1 3 = ( 2 C xx +1 ) ( 2 C yy +1 ) -4 C xy , I = 2 ( Cxx T t + Cyy T t ) + 3, 1 = ( 2Cxx T t + 1 ) ( 2 Cyy T t + 1 ) -
- 4 ( Cxy T t ) ; Cxx T t , С yy T t , Cxy T t - компоненты тензора деформаций, отражающие переход из промежуточной конфигурации (соответствующей времени т ) в текущую конфигурацию (соответствующую времени t ).
2. Выполнение процедуры линеаризации исходной постановки с учетом структурных и температурных деформаций
Рассматриваемый в данной работе алгоритм предполагает линеаризацию постановки (9), что позволяет свести процедуру получения решения исходной нелинейной задачи к решению последовательности линейных упругих краевых задач в рамках теории малых деформаций. Линеаризация геометрических соотношений может быть выполнена путем разложения исходного движения тела на совокупность малых движений, вызываемых малыми приращениями внешних воздействий. Согласно идее наложения малых деформаций на конечные [21, 22], движение тела из начальной конфигурации в конечную представимо в виде суперпозиции движений тела через промежуточные конфигурации. Таким образом, перемещения тела в произвольный момент времени представимы в виде суммы накопленных и малых перемещений, описывающих переход из промежуточной конфигурации в конечную.
Рассмотрим движение тела, приводящее его к моменту времени t из начальной недеформированной конфигурации С 0 в конфигурацию Сt , через промежуточную конфигурацию Ct _д t . Положение некоторой точки в начальной конфигурации определим радиусом-вектором r , в конфигурациях Ct _д t и Ct радиусом-векторами R 0 и R соответственно. Пусть U и u – векторы перемещений, переводящие тело из конфигурации С 0 в Ct _д t и из Ct -д t в Ct соответственно. Каждый из этих векторов является функцией обобщенных координат q1 , i = 1,2,3. Предполагается, что конфигурация Ct -д t близка к конечной и, соответственно, перемещения u малы.
В конфигурациях С 0 , Ct -д t введем обычным образом локальные основные и сопряженные базисы
, R o , r = g^, R oi = G R d q d q
+ V U o - V u + V U o -
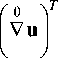
0 T
+ V U o -V u -I V U o I +
где g ij и G ij – контравариантные компоненты метри ческого тензора в начальной и промежуточной конфи гурациях соответственно .
Операторы Гамильтона в конфигурациях С 0 и C t Л t определены следующим образом :
+ V U o -
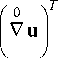
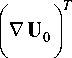
5 0 -
V = r s —, V = Ro s d q s 0
d dqs
Тогда тензоры - градиенты места , описывающие пе реход из начальной конфигурации в промежуточную , из промежуточной в конечную и из начальной в конечную , могут быть записаны в виде
Fo =(VRo)T =(V(r + U))T ,
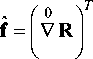
v ( R o + u )
где U 0 – вектор перемещений из начальной конфигурации в промежуточную; u – вектор малых перемещений из промежуточной в конечную, операторы Гамиль-0
тона V , V определены относительно исходной и промежуточной конфигураций, тензор C ˆ0 соответствует деформациям, возникающим при переходе из начальной *
конфигурации в промежуточную, C – из промежуточной в конечную.
Для плоского деформированного состояния в декартовой системе координат операторы Гамильтона записываются следующим образом:
F =(VR)T =(V(Ro + u))T.
Градиент места F ˆ может быть представлен через тензоры F ˆ0 и f ˆ следующим образом:
A A A
F = f • F o .
|
" a Ux |
a U y |
0 |
|
|
a x |
a x |
||
|
V U o = |
a U x a y |
a U y a y |
0 |
|
o |
0 |
0 |
|
|
L |
С учетом этого тензор меры деформаций Коши-Грина записывается в виде
A A ^ A A ^ A ^ A A
G X = F T • F = F T • f T • f • F o.
Тензор меры деформаций Коши-Грина G X = f T • f , описывающий переход из C t A t в C t , с учетом малости u может быть преобразован к виду
— X
A
где
G X = 2 e + g ,
/ z \ 7 A
. 1 o o Y
e = - V u + V u
2 I J
V ; J
– тензор малых деформаций.
Тензор деформации Коши-Грина, описывающий переход из начальной конфигурации в конечную, записывается в форме
C = (GX - g)/2 = (FoT • Fo - g)/2 + FoT • e • Fo
и может быть представлен в виде
A A A
C = C o + C
*
C o = 2 ( V U o + ( V U o ) T + V U o ( V U o ) T ) ,
00 T 0 T 0 TT
C = Vu + IVu I +Vu-IvUo I + IVu I -IvUo I +
, Г, 5 U 5 Uy ) 5 Uy d U ветственно, A = I 1 +-----111 +-----I---
V 5x J V dy J 5x dy
Окон-
чательно для плоского деформированного состояния в декартовой системе координат линеаризованные геометрические соотношения имеют вид
d Ux - fg Ux Y - f d Uy J
dx 2 V dx J 2 V dx J
н—
A
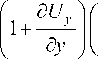
1 5 Ux J
1 + —- I dx J
a Ux a U y a y a x
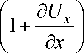
a ur —x+ ax
+1 ff1+dUx)f1+dUy IdUy -dUx faUy у Iduy a V ax JI ay J ax ay lax J ax,
d U y 1 fd U Y - fd U y J 2
C =-+— x +—yy dy 2 V dy J 2 V dy J
+
|
1 + — |
[ |
f 1 +d U y 1 2 |
fi 5 Ux 1 +---- |
) 8 Ux |
8 U y |
f1 + 8JUr 11 |
5 u , —- + |
|
A |
L |
k d y J |
k 8 x |
J d y |
d x |
k 8 y J |
d y |
|
1 + — |
2 8 Ux V 1 + |
' 1+d U y |
8 Ux x |
f d Ux x |
) 2 fd U y I |
8 ux x |
|
|
A |
Lk d x |
8y / |
d y |
k 8 y |
J k 8 x J |
d y |
|
( P ii ) xy = ( P ii ) xy +
1 P -- ' ) xy ( C ." )
8 C yy
d ( P ii a ) x, ( C 0 )
A C„ + 2
8 C xx
A Cxx +
1 P a ) x , ( C j )
8 CXy xy
A C + xy
|
1 |
8 Ux d U , a Ux 8 Ux d U , d U , |
||
|
Cxy = |
—- + —- + —-—- + —-—- |
+ |
|
|
2 |
8 y d x d x d y d x d y |
||
|
1 d Ur |
[_ |
dU 8 U , aU 8 U y d U y a U ’ |
8 ux |
|
+--- |
1 +--- x +--- + +---x ---3---3-- x |
||
|
2 A d y |
L |
5 x d y a x a , a x a , |
d x |
|
1 8 U , +--- |
Г 8 U d U y d U 8 U , d U y d U " 1 + — x + —^ + — x i---i-- x |
d и , |
|
|
2 A d x |
L |
a - a , a x a , a x a , |
d y |
a
+ J
‘P i k P ) xy ( C “)
8 C xx T t
A Cxx +
1 P i k P ) xy ( C j )
8 C yy T t
A C yy +
где, например,
+ 2
d ( v )„( Ci;6 ) I
—-------- A С, 2
d C t xy
xy
,
i L 8 U +— i+—-
2 Д, d x
. d U a Uy d U a u, a u, a U i+—-+—++—x—i- a- ay ax a, ax a,
, d U а и a U a и
1+-++- dx dy dx dy
8 U y d U x p u ,
.
d x d y _ d x
Процедура линеаризации физических соотношений состоит в разложении соотношения (8) в ряд Тейлора с учетом только линейных слагаемых. В результате линеаризованные физические соотношения, определяющие компоненты тензора Пиолы-Кирхгофа второго рода P ˆ II , принимают вид
( Pn L =( Pii t ' PII gx:' Cij ^ A C + xx xx
d ( Pn a ) ( C 0 ) d ( P a ) ( C y 0 )
+ A Cyy +2 ~ A Cxy + d Cyy d Cxy
a|
+ J
? 'И P I ” ) xx ( C « )
a Cxx T t xx
+ 2 ■ P P ) xx ( C" )
a c-T t
d ( Pn P) ( C^ )
A C + ---- 7 xxV 7
ac T t yy
A C yy +
A C„ xy
,
0 d ( P iia ) ( C i, 0 )
( Pii ) yy =( Pii )0yy + A Cxx + xx
d ( PH 3 ) yy ( C i, 0 ) 8 C yy
A C yy
+ 2
1 P « ‘ ) yy (" )
8 Cxv xy
AC xy
+
d ( P ii a
xx
8 Cxx xx
{^ a [- 3 1 3 . 4s ( 2 c ,, + 1 ) -
- 2 ( 2 C yy + 1 ) Г i 4 s - 4 - 7Г. (2 1) ^
S \ 3 3 13 y УУ 7 I
+
+ B a ( 2 C yy + 1 ) [ 2 + 1 s - 32 ( 2 C yy + 1 ) _ } ( 1 -a ( t ) ) ,
d ( P ii a) { 9 Г
-A---- A t = { - 2 ц а i -41 s ( 2 Cxx + 1 ) -
3 xx
8 C yy I 3 L
- ( 2 C yy + 1 ) ( i - 4/S - 3 1 1 1 3 - 7/S ( 2 C xx + 1 ) ) +
+ B a ( 2 CH + 1 ) [ 2 + 1 s - 32 ( 2 C xx + 1 ) _ } ( 1 - a ( t ) ) ,
d ( P ii a ) f xx =
3 C xy "I
- B a 8 C xy
a 8
ц 3 Cxy
i s - 43 - 3 1 1 1 s - 7/s ( 2 C yy
1 + 2 i s - 32 ( 2 C„ + 1 ) ( 1 -a ( t ) ) ,
d( Pn KP)
xx
d C xx T t
-
X 2 1 3
a( t ) Г 1
= J {-2 ' (2Cyy о L 3
,T t + 1 ) x
43 - 4 ix i - 73 ( 2 C yy T t + 1 )
+
+ B kP ( 2 C yyTt + 1 ) L 2 + i s - 32 ( 2 C yyTt + 1 ) _} d a ( T ) ,
a ( t )
+ J
' P i k P ) yy ( У" )
8 C xx T t
A Cxx xx
( P i k P ) yy ( C j ) A C
T t -
+
d ( P ii KP ) xx
8 C yyT t
+ ( 2 C yy T t +
+ B kP ( 2 C xx
a ( 1 ) Г
= С {- 2 Ц кp о L 3
i 3-4/s( 2 C X T t + 1 +
3 xx
4 ixi - 7^ ( 2 C xxxt
+
: T t + 1 ) [ 2 + 1 - 32 ( 2 C yy т t + 1 ) ] } d a ( T ) ,
+2 d ( P ik P ) yy ( C i, -) 8 C xy T t
AC xy
d( P nKP ) a( t )r
У _______ / xx _ Г { kp 8 t t
Tt = J Г 3Cxy дCxy о L 3
Г - 4/3 4 - - - 7/3
3 3 13
( 2 C„ ''
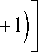
|[ ( P ii ) 0 + 4 D a ( C 0) ■■
V 0 L
- B кр 8 C / t xy
1 + 2 I ( 2 C yyTt + 1 ) d а ( т ) .
Величины A C ij - приращения компонент тензора деформаций Коши-Грина на рассматриваемом шаге.
При построении физических соотношений в случае использования нелинейных уравнений состояния существенным является вопрос учета температурных деформаций материала. Ряд авторов [23, 24] предлагают использовать введение линейного слагаемого, зависящего от приращения температуры, аналогично тому, как это принято в случае использования линейных соотношений. В работе [25] используется подход, основанный на линеаризации физических соотношений и предположении о малости температурных деформаций на рассматриваемом переходе. Очевидно, данная методика обладает большей общностью, хотя сразу стоит отметить существенные сложности реализации, связанные с необходимостью выделения упругой механической составляющей кинематики процесса.
В настоящей работе рассматривается вопрос построения численного алгоритма решения задач определенного класса (определения технологических напряжений в ходе процесса получения полимерных изделий), в которых деформации, являясь значительными по величине, все-таки остаются умеренными (порядка 10 %). С учетом ограниченности деформаций в рассматриваемом процессе линеаризованные физические соотношения в матричном виде могут быть записаны следующим образом:
P ii ( t ) = ( P 11 ) 0 + 4 D a(< C 0) ■■ а ( t )
■■ ( F o r ■ ( e - e e ) - F o ) (1 -а ( t )) + J 4 D кр( C t 0) ■■
■■( Fo ■(e- ee)-Fo) d а(тх где ee - тензор суммы малых температурных и структурных деформаций, возникающих при переходе из промежуточной конфигурации в конечную; e e = КТ (Т (t) - Т)) E - для аморфной фазы;
ee= КТР (Т(t) - Т(t))E - kE - для кристаллической фа зы; КТ, К^р - коэффициенты температурного расширения для аморфной и кристаллической фаз соответственно; к - коэффициент структурной усадки; E - еди-т0
ничный тензор; тензор C описывает переход из конфигурации, соответствующей моменту времени т, в промежуточную; 4 ID a, 4 D кр - тензоры четвертого ранга «касательных жесткостей» аморфной и кристаллической фаз, компоненты которых зависят от C 0 и C т 0.
С учетом выполненных процедур линеаризации выражение (9) может быть преобразовано к виду
а ( t )
■■ ( F ■ ( e - e e ) ■ F ) (1 -а ( t )) + J 4 D кр ( C т 0) ■■
-
■■ ( F 0 T ■ ( e - e e ) . F 0 ) d а ( т )]-5С * dV0 = 0. (11)
-
3. Разработка и реализация численных процедур решения поставленных краевых задач
Таким образом, определение эволюции поля перемещений с течением времени сводится к решению последовательности линеаризованных задач относительно приращения вектора перемещений на временных шагах.
Получение решения краевых задач механики для тел сложной пространственной конфигурации невозможно без использования численных методик. Среди существующих численных подходов в настоящее время наиболее широко применяется метод конечных элементов [26], который и был выбран для построения дискретного аналога рассматриваемой задачи. Применение конечно-элементного подхода к аппроксимации геометрических и физических соотношений приводит к получению линейных алгебраических соотношений, которые могут быть представлены в матричной форме [26]:
{C}={C0}+ [B(x,U0)]{6e},
{ P } = { P 0 } + [ Da ( U )] ( [ B ( x,U 0 )] { б e } - { A C e } ) (1 - а ( t )) + J t ) [ Dкр ( U 0 t )] ( [ B ( x, U 0 t )]{ б e } - { A C e } ) d а , 0
где { б e } - вектор узловых неизвестных (приращений перемещений на рассматриваемом шаге); [ B ( x,U 0)] -матрица градиентов элемента; { A C e } - вектор приращения температурных и структурных деформаций; [ D a( U 0)], [ D кр ( U 0 t )] - матрицы «касательных» жесткостей аморфной и кристаллической фаз материала.
Последнее соотношение может быть преобразовано к виду
{ P } = { P 0 } + [ D ( U 0 )][ B ( x U 0 )]{3 e } - [ D ( U )]{A C 8},
а ( t )
где [ D ( U 0 )] = [ D a( U 0 )](1 -а ( t )) + J [ D кр( U 0 T )] d а .
В матричной форме соотношение (8) можно записать как
Е ( [ к ] e б e - { fp } e - { f e } e ) = 0,
e где ^ означает суммирование по элементам; [к]e -e локальная матрица жесткости элемента; {fP}e, {f e}e -локальные векторы узловых сил, обусловленные наличием накопленных напряжений, температурными и структурными деформациями:
[ k ] e = f [ B ( x,U o )f[ D ( U o )][ B ( x,U o )] dV ,
V 0 e
{ f p } e = f [ B ( x,U o )f { P o }dV ,
V 0 e
{ f > } e = -f [ B ( x,U o )f[ D ( U o )]{ A C 6 } dV .
V 0 e
В результате сборки глобальной системы для всего ансамбля конечных элементов получим
[ K(U o ) ]{ u } = { F p } + { F 9 } , (12)
где [ K(U 0) ] - глобальная матрица системы, обладающая симметрией и зависящая от вектора накопленных перемещений U 0 ; { F p } , { F g } - глобальные векторы «фиктивных» усилий, обусловленные накопленными к рассматриваемому шагу напряжениями и возникающими на рассматриваемом переходе температурными и структурными деформациями.
Таким образом, получаем последовательность линейных задач, сформулированных относительно приращений узловых перемещений. Оператор левой части соотношения (12) требует переопределения на каждом шаге, что обусловливает существенную вычислительную нагрузку при решении задач большой размерности.
Для случая решения двумерных задач рассматривается построение конечно-элементного алгебраического аналога с использованием трехузлового конечного элемента с линейной аппроксимацией узловых неизвестных, в качестве которых приняты приращения перемещений. Все соотношения получены в базисе исходной конфигурации.
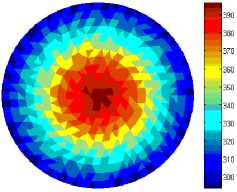
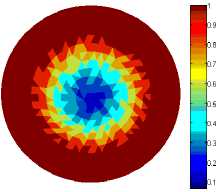
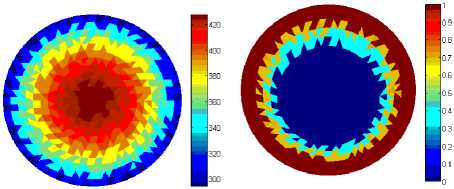
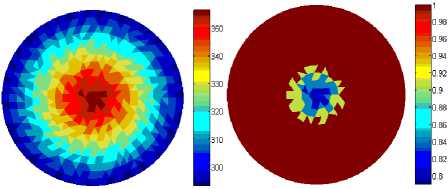
зависимость удельной теплоемкости, коэффициента теплопроводности и плотности полиэтилена от температуры взяты из литературных источников [28–30]. При решении задачи определения НДС конструкции задавались кинематические граничные условия, гарантирующие отсутствие смещений тела как абсолютно жесткого. Эволюция полей температуры и степени кристаллизации представлена на рис. 1. Закономерности эволюции раковины в цилиндре иллюстрируются рис. 2.
б
4. Решение модельной задачи описания эволюции дефекта типа раковиныв кристаллизующемся полимерном цилиндре
Рассматривается задача о протекании процесса кристаллизации и формировании дефекта типа раковины в полимерном цилиндре. Изначально материал цилиндра (полиэтилен) имеет температуру 430 К, что превышает температуру плавления. Цилиндр диаметром 0,2 м охлаждается по внешнему контуру водой, температура которой составляла 293 К. При решении теплокинетической задачи на границе тела задаются условия конвективного теплообмена. Коэффициент теплоотдачи на поверхности принимается равным 550 Вт/(м2 - К). В процессе охлаждения в материале протекают процессы кристаллизации, сопровождающиеся выделением тепла.
Краевая задача нестационарной теплопроводности решалась методом конечных элементов. Для решения задачи кинетики кристаллизации использовался разностный метод Рунге-Кутты [27]. Учитывалась зависимость тепломеханических свойств от температуры. Значения теплофизических и механических параметров,
Рис. 1. Распределение температуры и степени кристаллизации для моментов времени: а – 7800 с; б – 22800 с; в – 37800 с Fig. 1. Distribution of temperature and crystallization degree for time instants: а – 7800 s; b – 22800 s; c – 37800 s
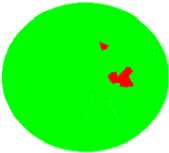

Рис. 2. Образование раковины для моментов времени: а – 16550 с; б – 17550 с; в – 18300с; г – 19550 с
Fig. 2. Formation of the shell for time instants: а – 16550 s; b – 17550 s; c – 18300 s; d – 19550 s
б

г
а
в
Заключение
Таким образом, выполнена формулировка двумерных наследственных краевых задач нелинейной термомеханики кристаллизующихся полимерных материалов в рамках теории конечных деформаций. Предложен и реализован метод линеаризации исходной постановки с учетом структурных и температурных деформаций. Разработан и реализован численный алгоритм решения поставленной плоской краевой задачи с целью исследования особенностей эволюции напряженно-деформированного состояния в полимерной конструкции. Получено численное решение модельной
Список литературы Численное исследование термомеханического поведения кристаллизующейся полимерной среды с учетом больших деформаций
- Production stresses during the solidification of cylindrical articles formed from polymer composite materials/V.N. Korotkov, R.A. Turusov, E.A. Dzhavadyan, B.A. Rozenberg//Mechanics of Composite Materials. -1986. -Vol. 22. -No. 1. -P. 99-103.
- Shaffer B.W., Lewitsky M. Termoelastic Constitutive Equation for Chemically Hardering Materials//Journal of Appl. Mech. -1974. -Vol. 41. -No. -P. 652-657.
- Lewitsky M., Shaffer B.W. Residual Thermal Stresses in a Solid Sphere Cast From a Termosetting Material//Journal of Appl. Mech. -1975. -Vol. 42. -No. 9. -P. 651-655.
- Golotina L.A., Matveenko V.P., Shardakov I.N. Analysis of deformation process characteristics in amorphous-crystalline polymers//Mechanics of Solids. -2012. -Vol. 47. -P. 634-640 DOI: 10.3103/S0025654412060040
- Boyce M.C., Socrate S., Llana P.G. Constitutive Model for the Finite Deformation Stress-Strain Behavior of Poly(Ethylene Terephthalate) above the Glass Transition//Polymer. -2000. -Vol. 41. -No. 6. -P. 2183-2201.
- Rebecca B. Dupaix, Mary C. Boyce. Constitutive modeling of the finite strain behavior of amorphous polymers in and above the glass transition//Mechanics of Materials. -2007. -No. 39. -P. 39-52.
- Modeling and Validation of the Large Deformation Inelastic Response of Amorphous Polymers over a Wide Range of Temperatures and Strain-Rates/J. Richeton, S. Ahzi, K.S. Vecchio //Int. J. Solids Struct. -2007. -No. 44. -P. 7938-7954.
- A Thermo-Mechanically Coupled Theory for Large Deformations of Amorphous Polymers. Part I: Formulation/L. Anand, N.M. Ames, V. Srivastava, S.A. Chester//Int. J. Plast. -2009. -Vol. 25. -No 8. -P. 1474-1494.
- A thermo-mechanically-coupled large-deformation theory for amorphous polymers in a temperature range which spans their glass transition/V. Srivastava, S.A. Chester, N.M. Ames, L. Anand//International Journal of Plasticity. -2010. -No. 26. -P. 1138-1182.
- Varghese A.G., Batra R.C., Constitutive Equations for Thermomechanical Deformations of Glassy Polymers//Int. J. Solids Struct. -2009. -Vol. 46. -No. 22. -P. 4079-4094.
- Finite Deformation Thermo-Mechanical Behavior of Thermally Shape Memory Polymers/H.J. Qi, T.D. Nguyen, F. Castroa et al.//J. Mech. Phys. Solids. -2008. -Vol. 56. -No. 5. -P. 1730-1751.
- Liu C., Qin H., Mather P.T. Review of progress in shape-memory polymers//J. Mater. Chem. -2007. -Vol. 17. -P. 1543-1558.
- Thermomechanics of shape memory polymers: uniaxial experiments and constitutive modeling/Y.P. Liu, K. Gall, M.L. Dunn, A.R. Greenberg, J. Diani//Int. J. Plast. -2006. -Vol. 22. -P. 279-313.
- Dietsch B., Tong T. A review: features and benefits of shape memory polymers (SMPs)//J. Adv. Mater. -2007. -Vol. 39. -P. 3-12.
- Gunes I.S., Jana S.C. Shape memory polymers and their nanocomposites: a review of science and technology of new multifunctional materials//J. Nanosci. Nanotechnol. -2008. -Vol. 8. -P. 1616-1637.
- Simulation of Thermomechanical Processen in Crystallising Polymer/I.N. Shardakov, V.P. Matveyenko, N.V. Pistsov, V.P. Beghishev//Polym. Eng. and Sci. -1997. -Vol. 37. -No. 8. -P. 1270-1279.
- Degree of crystalline structure of polymer obtained from melt at various cooling rates/A.Ya. Malkin, S.A. Bolgov, V.P. Begishev, O.S. Mazalov//Journal of Engineering Physics and Thermophysics. -1991. -Vol. 61. -No. 3. -P. 1092-1095.
- Новокшанов Р.С., Роговой А.А. Эволюционные определяющие соотношения для конечных вязкоупругих деформаций//Изв. РАН. Механика твердого тела. -2005. -№ 4. -С. 122-140.
- Лурье А.И. Нелинейная теория упругости. -М.: Наука, 1970. -940 с.
- Методы прикладной вязкоупругости/А.А. Адамов, В.П. Матвеенко, Н.А. Труфанов, И.Н. Шардаков/УрО РАН. -Екатеринбург, 2003. -411 с.
- Роговой А.А. Определяющие соотношения для конечных упруго-неупругих деформаций//Прикладная механика и техническая физика. -2005. -№ 5. -С. 138-149.
- Куликов Р.Г., Куликова Т.Г. К вопросу определения деформированного состояния кристаллизующейся полимерной среды с учетом больших деформаций//Вестник Пермского национального исследовательского политехнического университета. Механика. -Пермь, 2012. -№ 1. -С. 62-72.
- Vikas Srivastava, Shawn A. Chester, Lallit Anand. Thermally actuated shape-memory polymers: Experiments, theory and numerical simulations//Journal of the Mechanics and Physics of Solids. -2010. -No. 58. -P. 1100-1124.
- Адамов А.А. Исследование и моделирование нестационарного термомеханического поведения вязкоупругих резиноподобных материалов и элементов конструкций при конечных деформациях: дис. … д-ра физ.-мат. наук. -Пермь, 2004.
- Rogovoy A.A. Formalized approach to construction of the state equations for complex media under finite deformations//Continuum Mechanics and Thermodynamics. -2012. -No. 24. -P. 81-114.
- Зенкевич О. Метод конечных элементов в технике. -М.: Мир, 1975. -541с.
- Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. -М.: Лаборатория базовых знаний, 2001. -630 с.
- Теплофизические и реологические характеристики полимеров: справ./под ред. Ю.С. Липатова -Киев: Наук. думка, 1977. -244 с.
- Пивень А.Н., Гречанная Н.А., Чернобыльский Н.И. Теплофизические свойства полимерных материалов. -Киев: Вища школа, 1976. -180 с.
- Нильсен Л. Механические свойства полимеров и полимерных композиций. -М.: Химия, 1978. -312 с.


