Численное исследование задачи перевода космического аппарата на круговой орбите

Приводятся результаты численного исследования задачи перевода космического аппарата на круговой орбите. Для решения задачи используется метод моментов Н. Н. Красовского. Входе исследования получены следующие результаты: множество компромисса между расходом топлива и временем быстродействия; зависимости времени быстродействия от различных начальных отклонений по углу, эксцентриситету и периоду обращения. Результаты, расчетов обработаны, и выведены простые зависимости для оценки минимально необходимого времени управления в задаче перевода.

Рассмотрим следующую задачу терминального уп равления динамической системой, описываемой систе мой обыкновенных дифференциальных уравнений:

dx

— = f ( x , и ), x (0) = x^ti , x ( T ) = x^k , x е R , dt

^в

Для этого необходимо и достаточно, чтобы для всех

векторов § = ( ^ 1 , § 2 ,

I ••• ■

., ^_n) выполнялось неравенство

n

t k

n

s

и е R" ,    и е U , t е [0, T ] .

i = 0

Тогда

П               Р "                  1/ у ^,a < l(J у^-g-(t)dt)/s'.

i = 0

n

Линеаризация уравнений в окрестности круговой орбиты дает следующую систему линейных дифференциальных уравнений [1]:

5с = Ax + Ви , x (0) = x °, x(T ) = x k , xе R ⁴,

n ип (t) =     X ^i °g,(t)

^ ⁿ i = 0

s '- 1

t k

n

n sign^ £i0gi (t), i=0

s '

n

^X "  = JX ^ g . ⁽ t ) ^dt

i = 0

,

и е

где A =

" 0

- 2

R ', | и | <  и, 0 1

m ,

t е [0, T ] ,

а вектор ^ и число X _п определяют по результату решения следующей задачи: найти

,

В =

t k

n

s tk

n

s

, x - отклонение

п                                  п‘ minJX^-g-(t) dt = JX^0-g-(t) dt =Xn ^l"s(7)

0 i=00

i = 0

i = 0

от круговой орбиты по радиусу; x ₂ - отклонение по радиальной скорости; x ₃ - отклонение по угловой скорости; x ₄ - отклонение по углу; и , - трансверсальное ускорение; и ₂ - радиальное ускорение; и _т - предельное значение ускорений. Все переменные - безразмерные, за единицу длины принята высота геостационарной орбиты R , = 42 164 км, за единицу времени взят период обращения КА на геостационарной орбите Т= 24 ч.

Метод моментов Н. Н. Красовского является одним из эффективных методов решения терминальной задачи оптимального управления линейной динамической системой. Его преимущества связаны с тем, что решение задачи сводится к минимизации выпуклой функции, размерность которой равна размерности уравнений движения, в результате чего не возникает необходимости решать краевую задачу, как в принципе максимума, или иметь задачу большей размерности, как в методах параметрической оптимизации. Для решения задачи управления с помощью этого метода требуется лишь знание собственных функций управляемой системы.

Суть проблемы моментов состоит в следующем. Пусть даны п линейно-независимых функций g i ( t ) , не равный

при условии

n

X ^. X i = 1 .                        (8)

i = 0

Применение этого результата к решению терминальной задачи управления в системе с постоянными параметрами

x = Ax + Ви , x (0) = x ₀,    x (T ) = x k (9)

нулю вектор моментов a i , i = 1, 2,

• •• ■

., n , функции и ( t ) ичис-

ло / >  0. Требуется найти условия существования функции u_n ( t ) е L (0, t k ), ¹ + -7 = 1,1 <  s < ^ , удовлетворяющей ус-

ловиям

ss tk

J g i ( t ) ^и п ( t ) ^dt = « i , i = 1, ²,

...,

п , и „ ( t ) < l .         ⁽³⁾

основано на представлении движения линейной системы по формуле Коши:

t k

• - x 0 + e - Atk xk =J e - Aт Ви (т) dт.(10)

Тогда вектор моментов вычисляют по начальным и конечным условиям:

a = -x0 + e-Atkxk,(11)

в случае перевода в начало координат a = - x ₀ . Векторы -функции

G (т) = e - Aт В(12)

являются собственными функциями динамической системы и представляют собой столбцы матрицы (12).

Уравнение (9) можно рассматривать как линейную операцию tk

• 9 и ⁽ h ^{( т ))} = J h T ^{( т )} и (г) d г ,               (13)

порожденную функцией и ( г ) в линейном пространстве B { h ( г ) } с нормой линейной операции р [ ф J i ( г )] в сопряженном пространстве В * ( и ( г ) } . Норму р [ р _и1 ( г )] находят по условию максимума:

t k

• р [ h ( г )] = max [ h^T ( г ) и ( г ) d г .              (14)

u 0

Для пространства L в (5) сопряженная норма равна L s . В других случаях ее нужно определять по условию (14). В данной работе рассмотрены интенсивности управления % ( и ) и сопряженной нормы р [ h ( т )] [2] (см. таблицу).

1	Ограничен модуль ускорения и моторное время
	Г max{sup | и ( т )|, X I | и ( т )| dт } 0 < т <  г            0	max J | h ( т ) | dт А
2	Ограничен модуль произвольно направленного ускорения и моторное время
	^          Г Л         v max{sup У и 2 ( т ), X [( У и 2( т ))^ di } 0 < т < г -f        0 £1	max J ( У и 2 ( т )) ^ dт А ' = 1 при а ( Л ) = min ( И , Т ) Ле [0, Г ] / X

Пусть в управляемой системе, описываемой (2), выбрана интенсивность % ₂[ и ] и определена норма р ₂ [ и ] функции и ( t ). Необходимо найти оптимальное управление и ⁰( t ), переводящее систему из x ⁰ в x ^k с минимальной интенсивностью % [ и ].

Задача имеет решение, если существует число р ⁰[ h ⁰( т )] > 0, где h ⁰( т ) - минимальная функция.Тогда интенсивность управления Д и ⁰ ] = 1/ р ⁰ и принцип максимума формулируется следующим образом:

следованы зависимости времени быстродействия от различных начальных отклонений по углу от л/18 до 2л, по эксцентриситету от 0,005 до 0,2 и по периоду обращения 0.. .3 600 с. Результаты расчетов были обработаны методом наименьших квадратов для определения простых зависимостей с целью оценки минимально необходимого времени управления в задаче перевода. Полученные за висимости для начального угла и соответствие оценки по формуле T = 1,15 ■     , где ЛХ -начальное отклонение по um углу; Т- время быстродействия, в сут приведены на рис. 3.

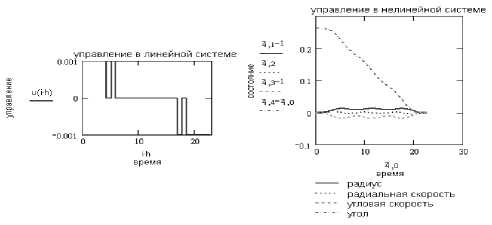
Рис. 1

ТТ

J[h^"Ог и°(т)dт = max J[h°(t)r и(т)dТ где h0(т) - решение задачи на условный экстремум:

mi

m

Z ^ 0 g ( т )

i = 1

= р [ h ⁰] = р ⁰

min р [ h ] = min р [У ^ g ( т )] = р

5                  5

m при У ^,х0 = -1.

i = 1

В случае отсутствия ограничений на расход топлива оптимальное управление имеет следующий вид:

и(t) = “ ■ siSn(h^t))’ h^t) = Z ^0 ■ gi (t).

P

Если ограничен модуль ускорения и время работы двигателей величиной ¹ = T a , то

Рис. 2

T

% [ и ] = max{sup | и ( т ) |, X J| и ( т ) | d т },

0 < т < T              0

р[h] = max J | h(т) | dт, Л А где Л - система отрезков на оси [0, T] суммарной длиной Л.

Решение задачи предельного быстродействия определится по условию

P ⁰ ( T ) = — .                  (17)

um

Документ MathCAD (рис. 1) иллюстрирует решение задачи быстродействия для перевода КА, находящегося на геостационарной орбите, на угол л/ 12 рад, с управляющим ускорением и = 0,001 и временем активного полета T a = 10 . Правый график получен путем численного интегрирования уравнений движения КА в ньютоновском поле (1) при управлении из левого графика, полученного по результатам решения задачи моментов (17). Точность перевода характеризует достаточную точность линейной модели (2) в задаче размещения КА на стационарной орбите.

В следующем документе MathCAD (рис. 2) показано множество компромисса между расходом топлива и временем быстродействия для перевода КА на угол 15 ° .

Для исследования предельных по быстродействию характеристик в задаче перевода КА были численно ис

Рис. 3

Для оценки минимально необходимого времени перевода от начального эксцентриситета получена формула _Т (0,7 ■ e + 38,6 ■ e ⁴)

T =--------------, а для начального отклонения по пе- и m

(AT -A T 2) риоду обращения - формула T = 0,936---------, кото- и m рая соответствует начальной орбите ниже геостационар-„ ,        _ ____(-A T + AT2)

ной, и формула T = 0,702-----------, адекватная орби- um те выше геостационарной.