Численное моделирование аэродинамических характеристик возвращаемых летательных аппаратов

Концепция пилотируемого перспективного воздушно-космического аппарата (ВКА) среднего класса (рис. 1) выдвигает ряд требований к его аэродинамическим характеристикам (АДХ), в частности, к аэродинамическому качеству. Проектирование ВКА осложняется тем, что существует целый ряд трудностей воспроизведения натурных условий полета в аэродинамических трубах (АДТ) [1]. В частности, практически невозможно воспроизвести тепловой режим при обтекании аппарата: нагрев модели в АДТ приводит к высокому значению температурного фактора, тогда, как в натурных условиях температура, поверхности аппарата значительно меньше полной температуры потока. Поток газа, набегающий на модель в АДТ, состоит из молекулярных кластеров и отличен от невозмущённой атмосферы, в которую входит спускаемый аппарат. Таким образом, уравнения состояния в натурном и трубном экспериментах различны.

Моделирование высокоскоростных течений предполагает соблюдение подобия по числам Маха, и Рейнольдса, а. также обеспечение низкой степени турбулентности и высокой однородности потока в рабочей части установки. На точность эксперимента серьезное влияние оказывает также способ закрепления модели. Одновременное решение этих проблем

в рамках одной экспериментальной установки представляется невозможным. Поэтому для исследования высокоскоростных течений применяются АДТ различной конструкции и с различными принципами действия [2-4].

Перечисленные факторы обуславливают необходимость привлечения расчетной информации на этапе проектирования ВКА. Детальные параметрические исследования можно проводить при помощи численного моделирования (компьютерных программ) [5]. В качестве таких инструментов выступают программные комплексы, реализующие различные модели движения среды. К числу таких комплексов относятся инженерные методы расчета, использующие гипотезу локальности высокоскоростных течений [6-8].

Рис. 1. Общий вид воздушно-космического аппарата. «Клипер»

Несколько слов следует сказать о сеточных методах - методах «высокого уровня». Они основаны на решении краевых задач (КЗ), корректность которых не доказана. Так, например, доказана, теорема, о том, что стационарное решение КЗ для уравнений Навье-Стокса в приближении несжимаемой жидкости существует и единственно для некоторого полуинтервала Re < Rei, неединствено в интервале Rei < Re < Re2 и не существует в полуинтервале Re Re 2 [9].

Таким образом, наряду с верификацией (доведением численной реализации метода, и компьютерного кода. на. конкретной вычислительной технике до такого уровня, когда, решение не зависит от параметров численной схемы) обязательна, валидация (согласование результатов расчёта, с экспериментом). При этом следует помнить, что это не гарантирует столь же хорошего согласования расчёта и эксперимента в других случаях.

Решаемые задачи имеют существенно нелинейный характер, то есть из аппроксимации уравнений и граничных условий и устойчивости численной процедуры не следует сходимость численного решения к решению исходной КЗ, как это имеет место для линейных задач (теорема. Лакса. [10]). Вопрос корректности разностной задачи для уравнений Навье-Стокса. остается открытым из-за. неясности граничных условий. Физически необоснованные и математически необоснованные граничные условия могут приводить к неустойчивости численного решения (например, на. выходной границе) [11].

Осреднение по Рейнольдсу уравнений Навье-Стокса требует выполнения условия эргодичности (наличия в течении только одного интеграла, энергии), что имеет место далеко не всегда. Осреднение по всему спектру частот приводит к тому, что не удается моделировать правильным образом, например, акустические нагрузки. Вопрос о справедливости самих уравнений Навье-Стокса при турбулентном режиме обтекания (линейная связь между тензорами скоростей деформаций и напряжений), да. и вообще, ньютоновость жидкости ставятся под сомнения [12].

Всё вышесказанное определяет место комплексам компьютерных программ, основанных на. инженерных подходах и аппроксимации баз данных, полученных в эксперименте.

2.    Метод расчёта

Для определения АДХ при больших сверхзвуковых скоростях использована модифицированная формула Ньютона: р = роcos²Ө, где ро - давление в точке торможения (по формуле Рэлея в гиперзвуковом приближении):

7 + 1         7

■• = (2Д)71 (1)71 [1 + 2L м-4 + 0 (М-4)]

где 1 - отношение удельных теплоёмкостей.

Несмотря на простоту, эта схема хорошо согласуется с экспериментом для широкого класса затупленных тел. Она предполагает, что частица газа, достигая поверхности тела, передает ему нормальную компоненту импульса, сохраняя касательную.

Распределения плотности и скорости на поверхности тела даются формулами:

р = ро (cos² Ө) ^ , ро = 2^Цро I" 1--2 М j + O (Му

⁷         1 — 1         1 — 1

^{V 2} = ^ [1 ^— (^cos20)"—'] ,

о             2 о

^Цт     ¹ '--, ^М j •

1 ^{— 1}

В случае заостренного симметричного выпуклого тела с углом при вершине /Зо, р = ро cos² Өо, г де Өо = тт/2 — /Зо, ^ПР^И обтекании с отошедшей ударной волной. Если же ударная волна присоединена, то ро определяется как давление на поверхности клина или конуса с углом полураствора /Зо- 0 < Ө < тт/2, т.е. рассматривается только та часть тела, которая видна со стороны набегающего потока. Точность аппроксимации ограничена предположением о локальности взаимодействия.

Для конуса под углом атаки используется формула р = ao + а1 cos Ө + Q2cos2Ө, 0 6 Ө 6 т.

Коэффициенты ац / = 0,1, 2, определяются из условий согласования с экспериментом: р(0) = ро, р(Ө_т) = р_т, р(Ө_т ) = 0. Более подробное описание метода и компьютерного кода может быть найдено в работах [6-7]. Как видно, результаты существенно зависят от отношения удельных теплоёмкостей у.

3.    Некоторые результаты

На рис. 2 дано сравнение расчетных результатов с экспериментальными данными работы [13], в которой эксперимент проводился с различными газами в вакуумной АДТ при числах М > 5. Видно, что расчетные и экспериментальные данные различаются менее чем на 10%.

Полученные результаты свидетельствуют о достаточно сильном влиянии вращательных степеней свободы, причем, существенно также влияние времени релаксации: чем оно меньше, тем более заметно это отличие от результатов расчетов при 1 = 5/3. Значение 1 для различных газов при разных темпуратурах приведены в таблице 1.

Таблица!

Значения 7 для различных газов при разных температурах

Температуры	Газ	7
-181 °C		1.597
-76 °C		1.453
20 °C		1.410
100 °C	Н2, водород	1.404
400 °C		1.387
1000 °C		1.358
2000 °C		1.318
20 °C	Не, гелий	1.660
20 °C		1.330
100 °C	Н2О, насыщенный водяной пар	1.324
200 °C		1.310
-180 °C	Аг, аргон	1.760
20 °C		1.670
0 °C		1.403
20 °C		1.400
100 °C		1.401
200 °C	сухой воздух	1.398
400 °C		1.393
1000 °C		1.365
2000 °C		1.088
0 °C		1.310
20 °C		1.300
100 °C	СО2, углекислый газ	1.281
400 °C		1.235
1000 °C		1.195
20 °C	СО, угарный газ	1.400
-181 °C		1.450
-76 °C		1.415
20 °C	О2, кислород	1.400
100 °C		1.399
200 °C		1.397
400 °C		1.394
20 °C	NO, окись азота	1.400
20 °C	N2О, закись азота	1.310
-181 °C	N 2, азот	1.47
15 °C		1.404

На рис. [2-4] представлены результаты расчетов коэффициентов аэродинамических сил и моментов в зависимости от угла атаки при различных значениях показателя адиабаты. Наибольший интерес представляют значения коэффициентов силы сопротивления С_ж, подъемной силы С_у, и момент а тангажа т_г.

4.    Заключение и выводы

Реализованный в виде компьютерного кода инженерный метод является по сути дела аппроксиматором экспериментальных данных и может подстраиваться под эксперимент в ходе валидации. С другой стороны, метод позволяет выбрать константы (коэффициенты) в уравнении состояния. Настроенное таким образом уравнение состояния может быть использовано в методах вычислительной аэродинамики более высокого уровня.

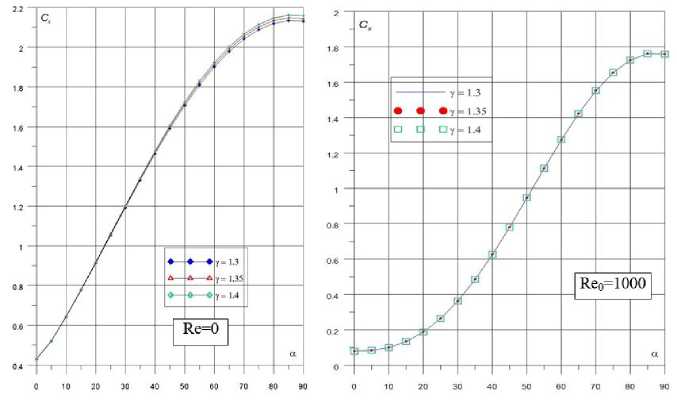
Рис. 2. Зависимости СДа) для ВКА «Клипер» при Ке0 = 0 и 1000 (7 = 1.3, 1.35, 1.4)

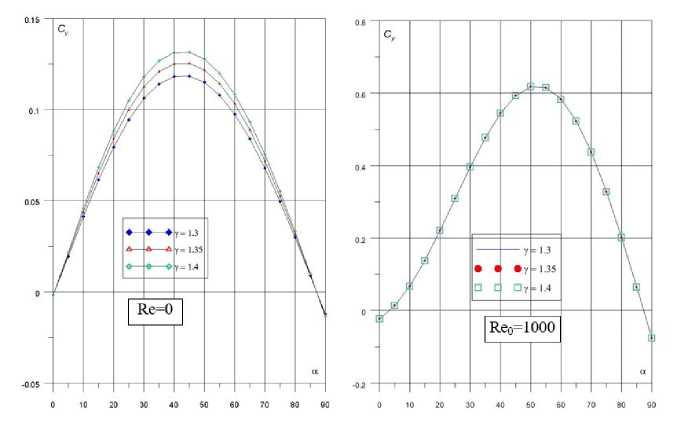
Рис. 3. Зависимости Су(а) для ВКА «Клипер» при Reo = 0 и 1000 (7 = 1.3, 1.35, 1.4)

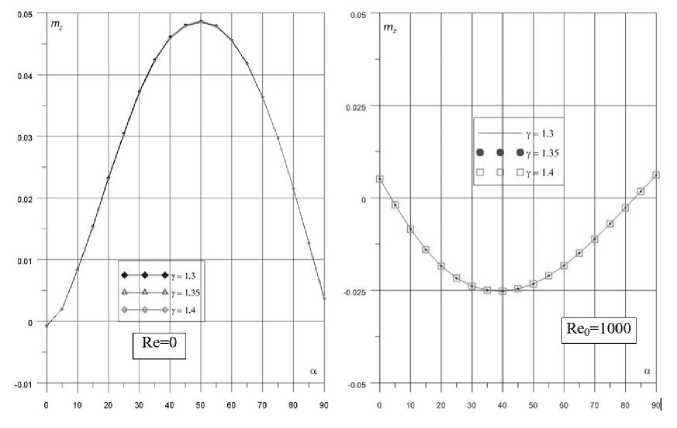
Рис. 4. Зависимости m _z (а) для ВКА «Клипер» при Reo = 0 и 1000 (7 = 1.3, 1.35, 1.4)

Настроенный под натурный эксперимент вариант данного компьютерного кода может быть использован на этапе предварительного проектирования в силу своей робастности и высокой скорости вычислений.

Вариант компьютерного кода, настроенный под модельный (трубный) эксперимент, может с успехом использоваться для выбраковки и сортировки экспериментальных данных, получении дополнительной информации к данным эксперимента и восполнении данных при их утере.