Численное моделирование депрессионного метода разложения газогидратов

Газовые гидраты — это твердые нестехиометрические соединения, образованные молекулами гидратообразующего газа, и молекулами воды. В газовых гидратах молекулы воды образуют кристаллическую решетку, в пустотах которой располагаются молекулы-гости. Такие соединения-включения называют клатратами. В естественных условиях наиболее распространены газовые гидраты метана, и углекислого газа, хотя встречаются и смешанные, в состав которых входят несколько газов. Считается, что газовые гидраты представляют собой твердый раствор, но в некоторых отношениях они ведут себя как химическое соединение. Следует также отметить, что разложение газовых гидратов происходит с поглощением тепла. В некотором диапазоне давлений и температур, представляющих интерес

для практических приложений, газовые гидраты разлагаются и образуют две фазы: жидкую, содержащую в основном воду, и газовую, содержащую в основном гидратообразующий газ. При фиксированной температуре разложение (диссоциация) газового гидрата происходит при определенном давлении Р = P_S(T ), что характерно для фазовых переходов в однокомпонентных системах.

Хотя процессы образования/разложения газогидратов относят к фазовым переходам, они в некоторых отношениях похожи на химическую реакцию. Основания для такого утверждения дает то обстоятелвство, что при образовании газогидрата на одну молекулу-гоств приходится фиксированное (хотя и не целое) число молекул воды, если отвлечвся от модификаций газогидратов. Другими словами, концентрация метана газа (молярная и массовая) в газогидрате фиксирована. Кроме того, фиксированы составы и остальных фаз: вода, лед, газ. Это вырождение позволяет изобразить фазовую диаграмму на плоскости температура-давление. В силу указанного обстоятельства число термодинамических степеней свободы в системе, содержащей газогидрат, уменьшается на единицу. Однофазная система (газогидрат) имеет две степени свободы, а не три, как следует из правила фаз Гиббса.

В дальнейшем для определенности будем рассматривать гидраты метана. Рассмотрим двухкомпонентную систему гидратообразующий газ (СН4)-вода (Н2О). Химическое соединение Н 2О может существовать в двух со стояниях: жидкая вода (индекс w) и лед (индекс г). Газ (индекс д), растворяясь в воде (как химическом соединении), образует фазу гидрат (индекс Ф). Молярная концентрация газа в этой фазе фиксирована, что отличает ее от обычных растворов и роднит с химическими соединениями. Химическое соединение Н2О может присутствовать в системе в виде жидкой воды, льда и в составе гидрата. Метан СН4 может присутствовать в виде газа и в составе гидрата.

Для моделирования разложения газогидрата и возникающего при этом многофазного течения использовался термогидродинамический симулятор, разработанный для численного интегрирования уравнений неизотермической фильтрации многокомпонентной смеси. Описание симулятора приведено в [4].

2.    Уравнения неизотермической многофазной фильтрации

В настоящей работе рассматривается упрощенная модель депрессионного метода разложения газогидрата. В рамках этой модели принимается, что газогидрат образован молекулами метана и воды. При некоторых термобарических условиях происходит разложение газогидрата на газовую (чистый метан СН4) и жидкую (чистая вода Н2О) фазы с поглощением некоторого количества тепла. Газовая и жидкая фазы подвижны и фильтруются через твердую матрицу, образованную скелетом и намерзшим на него газогидратом. Таким образом, рассматривается двухкомпонентная смесь (СН4 + Н2О), способная образовывать три фазы: газовую, жидкую и газогидратную. Исходно, термобарические условия в пласте таковы, что газогидрат находится в устойчивом состоянии в присутствии некоторого количества свободного газа. Другими словами, давление в пласте выше давления диссоциации газогидрата P_S(T ) при пластовой температуре и имеется некоторый переизбыток метана. Давление в пласте понижается путем стравливания газа через добывающую скважину. Так как давление в скважине принимается меньшим, чем P_S(T ), происходит разложение газогидрата с образованием подвижных фаз и понижением температуры.

Скелет (индекс s) образует поровое пространство, заполненое газовой (индекс д), водной (индекс w) и газогидратной (индекс Ф) фазами. Локально те или иные фазы могут отсутствовать. Пористость этого пространства (не заполненного газогидратом) m = const, абсолютная проницаемость К = const. Обозначим Sg, sw,sh — объемные доли газовой, жидкой и гидратной фаз в поровом пространстве, Sg + sw + s^ = 1. Течение жидкой и газовой фаз будем описывать в рамках обобщенного закона Дарси, гидратную фазу считаем неподвижной. Примем, что при диссоциации единицы массы гидрата образуется е единиц массы метана и 1 — е единиц массы воды. Для простоты будем предполагать, что жидкая фаза образована чистой водой (Н2О), а газовая — чистым метаном (СН4). В указанных предположениях уравнения баланса массы для метана и воды имеют вид

CH4

md⁰ (pg Sg + EphSh) + dlv/9_g W g = 0,

H2O

m⁰ (p™ s_w + (1 - E^phS^ + divp™ W™ = 0,

где p_g, p™, ph — плотности газовой, вод ной и газогидратной фаз, W_g, W™ — скорости фильтрации газовой и водной фаз.

Уравнение энергии имеет вид

Ot (m(sg pg eg + s ™ p™ e™ + s_hp_he_h ) + (1 - m)p_se_s') + div (pg hg W g + p™h_w W™ + q ) =0, (3)

где e_a,h_a — удельные әпергіш и энтальпии фаз (а = w,g,h,s) . Q = —kgradT — плотность теплового потока.

Теплоту фазового перехода гидрат ^ вода + метан (количество теплоты, необходимое для разложения единицы массы гидрата на метан и воду) q = (1 — е ) Һ ™ + Eh_g — Һ һ будем считать постоянной.

Водную и гидратную фазы будем считать несжимаемыми p™, ph = const, газовую фазу — идеальным газом.

3.    Численная модель

В основу рассматриваемой здесь численной модели, реализованной в термогидродинамическом симуляторе, положено выполнение законов сохранения масс компонентов смеси и энергии (1) - (3), записанных в виде

+ divJi = Si,   i = CH4, H2O, ot

ЭЕ

— + divJ = S, ot где Mi — эффективная плотность компонента i; Е — плотность внутренней энергии смеси; Ji, J — соответственно потоки массы и энергии; Si,S — источники/стоки массы и энергии (в данном случае — скважины).

Плотности компонентов, энергии и их потоков имеют вид

Мг = m'^paXi,asa, a

Ji  ^X_ W ,

a

Е =     paeaSa + (1 — m)p_se_s

a

Q = y^pahaWa — kgradT, a где sa — насыщенность фазы a (a = g,w,h',m- пористость «сухого» (не заполненного гидратом) скелета; pa — истинные плотности фаз, ea,ha — удельные внутренняя энергия и энтальпия фазы a; Xi,a — компонентный состав фазы а; к — эффективный коэффициент теплопроводности.

Для скоростей фильтрации фаз принимается закон Дарси:

W_a = — ^Ka gradF,

Pa где К — абсолютная проницаемость «сухого» скелета, Ka — относительные проницаемости фаз; pa — коэффициенты динамической вязкости фаз.

Для моделирования притока подвижных фаз в скважину использовалась формула Писмана, выражающая закон Дарси с учетом распределения давления в окрестности скважины. Согласно модели Писмена дебит фазы а из прямоугольного блока на единицу высоты перфорации составляет

2^KaPa Р -Pw

Jo

Ра   ln(r_b/r_w ) ^,

где P_w — давление в скважине, Р — среднее давление в блоке, r_w — радиус скважины, гь — эффективный радиус блока.

В изотропном случае эффективный радиус блока определяется соотношением гь = 0.14^2 + h_g, где h_x, h_y — размеры блока (расчетной ячейки).

Для численного интегрирования системы уравнений (4) использовалась консервативная разностная схема с расщеплением по физическим процессам и противопоточной аппроксимацией конвективных членов. Вычислительный алгоритм был реализован в виде термогидродинамического симулятора, описанного в [4].

4.    Численное моделирование4.1.    Постановка задачи

Задача о разложении газогидрата рассматривалась в двумерной постановке. Были выполнены расчеты двух вариантов, различающихся начальными данными. В начальный момент времени давление в расчетной области было постоянно и в обоих вариантах составляло Р = 20 МПа, соответствующая равновесная температура — Т = 18.7 °C. В первом варианте температура была ниже равновесной для начального давления (на 3 градуса) и отсутствовала водная фаза. Во втором варианте температура соответствовала условию фазового равновесия и присутствовали все три фазы. Температура и фазовые насыщенности были также однородны по пространству и составляли: в первом варианте

Т = 15.7 ⁰С, s_wo = 0, Sho = 0.92, Sgo = 0.08 .

во втором варианте

Т = 18.7 ⁰С, s_wo = 0.12, s_ho = 0.8, Sgo = 0.08 .

Значения основных физических параметров были позаимствованы в [2,3] и соответствовали (по заверению авторов) параметрам, характерным для Мессояхского газогидратного месторождения.

Плотности (воды, гидрата, скелета):

p_w = 1000 кгм³, p_h = 910 кгм³, p_s = 2800 кг м³:

Р плотность газа: pg = где R = 0.52 • 103 Дж/(кшК) — газовая постоянная метана;

RT коэффициенты вязкости (воды, газа):

p_w = 10^-3 Пах■, р_д = 0.014 • 10^-3 Пах;

удельные теплоемкости (воды, гидрата, газа, скелета):

c_w =4165 Дж (кг<К), с_д = 2500 Дж (кг4<), удельная теплота

ch = 3200 Дж (кг4<), cs = 873 Дж (кг4<):

диссоциации гидрата (учитывается в энтальпии гидрата):

q = 0.515 • 106 Дж кг:

массовая доля метана в газогидрате: Е = 0.1.

Зависимость давления диссоциации газогидрата от температуры принята в виде

„    .       Т (К) - 169.7

.

p (Па) = exp----7 28----

Абсолютная проницаемость «сухого» скелета K = 10 мД.

Относительные проницаемости газовой и водной фаз были приняты в виде [2,3]:

Hg (s^ ,s) = (1 — s_h )³ {

1.044 — 1.7s + 0.6s2    при s < 0.9,

0    при s >  0.9 ,

Hw (s^, s)    (1 s^) /

1.477s⁵ — 1.587s⁶ + 1.11s⁷ — 0.0473    при s >  0.55,

0 при s 6 0.55, где s =-----эффективная водонасыщенность.

• 1    — s_h

4.2.    Результаты расчетов

Неизотермическое фильтрационное течение рассматривалось в области 100 х 100 м. Разложение газогидрата инициировалось «включением» добывающей скважины, располо-женой в центре области. Радиус скважины составлял r_w = 10 см, давление в скважине P_w = 2 МПа. На внешней границе области ставились условия непротекания для всех фаз и теплоизоляции для температуры. В расчетной области вводилась равномерная сетка с шагами h_x = 1 м, h_g = 1 м. Шаг интегрирования по времени выбирался автоматически.

а)

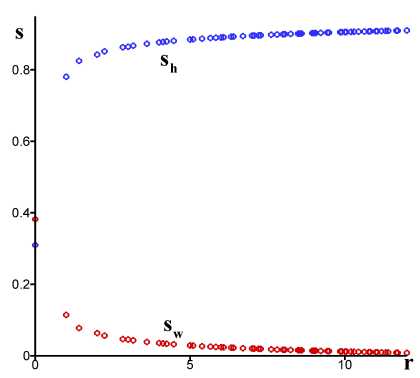
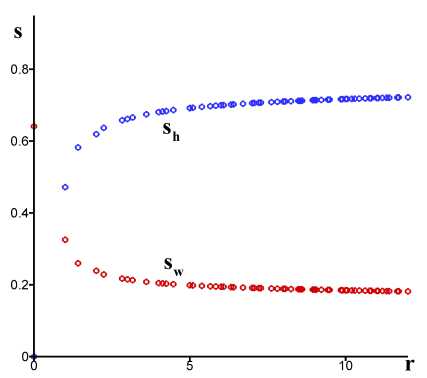
Рис. 1. Распределения гидратонасыщенности s^ (синие маркеры) и водонасыщенности s_w (красные маркеры) на момент времени ^ 120 сут. На левой панели а) представлены результаты численного моделирования диссоциации переохлажденного гидрата, на правой панели б) — результаты численного моделирования диссоциации равновесного гидрата

б)

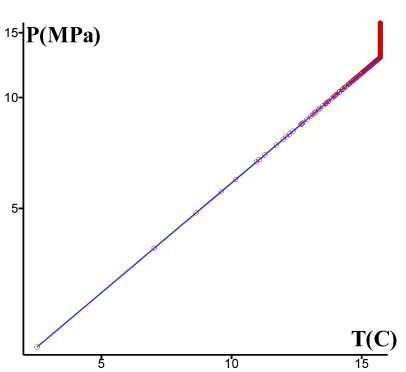
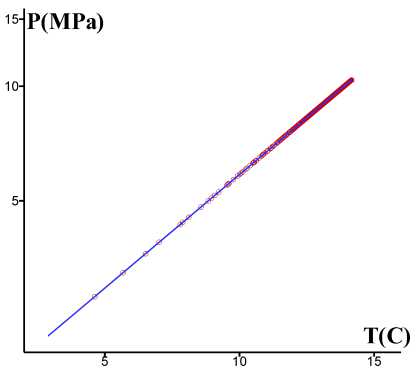
На рис. 1, 2 представлены результаты моделирования на момент времени ^ 120 сут. На рис. 1 показаны распределения гидратонасыщенности S^ (синие маркеры) и водонасыщенности S_w (красные маркеры) в расчетных ячейках, находящихся в окрестности скважины (на расстоянии не более 12 м.). Видно, что понижение давления приводит к разложению газогидрата. Симулятор с хорошей точностью воспроизводит аксиальную симметрию возникающих течений. На рис. 2 показаны (Т, P )-диаграммы, построенные по распределениям полей температуры и давления. На плоскости (Т, P ) красными маркерами показаны термобарические состояния во всех расчетных ячейках, сплошной синей линией показана зависимость равновесного давления от температуры (ось давлений представлена в логарифмической шкале). В первом варианте на кривой фазового равновесия лежат маркеры, представляющие термобарическое состояние в ячейках в окрестности скважины. Во втором варианте все маркеры лежат на кривой фазового равновесия.

а)                                                      б)

Рис. 2. (Т,Р )-диаграммы на момент времени ^ 120 сут. На левой панели а) представлены результаты численного моделирования диссоциации переохлажденного гидрата, на правой панели б) — результаты численного моделирования диссоциации равновесного гидрата

5.    Заключение

В работе выполнено математическое моделирование разложения газового гидрата де-прессионным методом. Для расчета многофазного течения, возникающего в результате диссоциации газогидрата, использовался термогидродинамический симулятор, разработанный для численного интегрирования уравнений неизотермической фильтрации многокомпонентной смеси [4]. Были выполнены расчеты процесса диссоциации как переохажденного газогидрата (начальная температура ниже равновесной при начальном давлении), так и равновесного газогидрата (начальная температура равна равновесной при начальном давлении). В обоих случаях термогидродинамический симулятор продемострировал высокую эффективность.

Работа выполнена при поддержке РФФИ, проект № 16-29-15123.

Авторы благодарят И. В. Цыбулина, без помощи и консультаций которого данная работа была бы невозможна.