Численное моделирование дифференциальных сечений рассеяния очень холодных нейтронов на сплошном бесконечном круговом цилиндре

Введение1

Макроскопические2 свойства3 вещества, такие, как4 теплопроводность, электропроводность, прочность, эластичность и т.д., зависят в основном от элементов структуры с характерными размерами от единиц до сотен нанометров. В последние годы повышенный интерес вызывает получение полимерных нанокомпозитов, содержащих наноразмерные наполнители. Введение углеродных наполнителей в полимерную матрицу является перспективным направлением в процессе создания новых материалов с улучшенными свойствами. Использование многослойных углеродных нанотрубок должно привести к созданию многофункционального материала с высоким модулем упругости и большой электропроводностью и теплопроводностью [1].

Очень холодные нейтроны (ОХН) – нейтроны, двигающиеся в вакууме со скоростями 5 <  v n <  100 м/с, т.е. c энергий 5 •Ю ^{- 7} <  e n < <  5 • 10 ^{- 5} эВ и длиной волны де Бройля 1 <  X _v <  100 нм, являются уникальным инстру-

ВЕСТНИК 2013 № 4

ментом исследования наноструктурированных материалов, поскольку эффективно и на большие углы рассеиваются на таких структурах. При таких энергиях отчетливо проявляются волновые свойства нейтрона, при взаимодействии нейтронной волны с препятствием меняется состояние ОХН, состояние же мишени не изменяется. Теоретические и экспериментальные исследования, выполненные в работах [2–6], показали, что рассеяние ОХН определяется размером, концентрацией и формой рассеивающих частиц, параметрами распределения частиц наполнителя в полимерной матрице. Для изучения наноструктурированных материалов проводится исследование зависимостей сечений упругого некогерентного рассеяния ОХН от длины волны нейтрона, получаемых при пропускании пучка нейтронов через образец («метод ослабления»). Этот метод позволяет получить информацию о наноструктуре исследуемых материалов (см. [6] и указанные там ссылки).

Он дополняет хорошо развитые методы малоуглового рассеяния рентгеновских лучей (МУРРЛ) и малоуглового рассеяния нейтронов (МУРН). Анализ экспериментальных результатов, полученных этими методами, основан на борновском приближении теории возмущений, поскольку есть малый параметр в задаче; например, в методе МУРН это параметр U / ε _H , где U – рассеивающий потенциал, ε _H – энергия налетающего на мишень нейтрона. Для тепловых нейтронов ( s H — 0.025 эВ) этот параметр ~10 ^{- 4} . В случае ОХН существует область энергий, когда энергия нейтрона ε _H близка к граничной энергии U_гр , при которой происходит полное внешнее отражение и U / E H — 1. В этом случае в качестве малого параметра задачи следует выбрать параметр ξ ≡ ( U / ε _H ) ⋅ ka < 1. Здесь k = 2 π / λ _v – это волновое число, a – характерный размер неоднородности, λ _v – длина волны де Бройля. Цель настоящей работы – рассмотреть и сравнить поведение решений задачи рассеяния – точного решения и первого борновского приближения для ОХН.

Теория

Метод ослабления ОХН заключается в следующем. При прохождении пучка нейтронов через образец толщиной t интенсивность пучка меняется по закону I = I ₀ exp( - t Σ _t ) , где S =S +S , +S +S , t a inel incog el .

Здесь I0 – интенсивность падающего пучка; Σt – полное макроскопическое сечение взаимодействия ОХН с веществом образца; Σa – макроскопическое сечение поглощения (Σa=nσa, n – плотность рассеивателей, σa – это микроскопическое сечение поглощения); Σinel и Σincog – макроскопические сечения неупругого и некогерентного рассеяния вследствие изотопического и спинового разупорядочения; Σel – макроскопическое сечение упругого рассеяния, соответственно.

Величина Σ _el может быть получена из значения Σ _t , если известен атомный состав образца и если возможно подавить Σ _inel охлаждением образца. Количество нейтронов, рассеянных в телесный угол 4 π – Ω _дет (Ω _дет – телесный угол, под которым виден детектор из мишени), равно ( I ₀ - I ). Задача сводится к определению усредненного по возможным ориентациям упругого сечения рассеяния рассеивателя. При вычислении Σ _el прежде всего используется борновское приближение, если удовлетворяется критерий ξ = ( U / ε _H ) ⋅ ka << 1 [7]. Здесь a – характерный размер рассеивателя (для шара, например, это радиус); k – волновое число налетающего нейтрона; U – оптический ядерный потенциал: U = ( Й ² /2 m ) • 4 п ^ N i b i . Здесь N i - плотность ядер i -го вида, b_i – длина когерентного рассеяния i -го ядра, Й - постоянная Планка, m - масса нейтрона. Параметры U и ε _H определяют в нейтронной оптике показатель преломления n ² = 1 - U / E = 1 - 4 π ∑ _iN_ib_i / k ² . Здесь длина когерентного рассеяния b_i =- f_i , f_i – амплитуда упругого рассеяния на i -ом ядре, b_i >  0 для большинства элементов периодической таблицы.

Для ОХН область значений, которые может принимать n , при рассеивании в вакууме: 0 ≤ n ≤ 1. Для нейтрона в вакууме n = 1; n = 0 – полное внешнее отражение; при k ² ≤ ≤ 4 π ∑ _iN_ib_i – это ультрахолодные нейтроны. Изменение фазы волны де Бройля, проходящей сквозь рассеиватель, например сквозь шар вдоль диаметра, равно ρ = 2 ak | n - 1| = 2 x | n - 1|. Процессы рассеяния оказываются совершенно различными в зависимости от того, велики или малы фазовые сдвиги по сравнению с единицей. Приближения, основанные на предположении, что фазовые сдвиги малы, в квантовой механике называются приближением Борна. В оптике существует строгая теория, достаточно хорошо описывающая область 1 ± ε ≤ n <∞ , – это теория Ми [8; 9]. В нашем случае область изменения показателя преломления 0 ≤ n ≤ 1. Если n = 1, то преломления, отражения и дифракции нет. С уменьшением скорости нейтрона показатель преломления также уменьшается: n → 0 , | n - 1| ^ 1; вблизи n — 0 возможен оптический резонанс.

В области достаточно больших r (r – это рас- стояние от рассеивателя до точки наблюдения), где оптический ядерный потенциал V(r) = 0, уравнение Шрёдингера сводится к скалярному волновому уравнению. Нанотрубки можно описывать как цилиндры, длина которых во много раз превосходит диаметр.

Построим точное решение задачи рассеяния на бесконечном сплошном круговом цилиндре радиуса R .

Пусть однородная плоская волна ψ_i = = exp( ik e _i x ), распространяющаяся в направлении вектора e _i = –sin ζ e _x – cos ζ e _z , падает на бесконечно длинный круговой цилиндр радиуса R . Ось цилиндра совпадает с осью OZ прямоугольной системы координат ( x , y , z ). Вектор e _i лежит в плоскости ( x , z ), образуя с осью z угол ζ . Волновой вектор k _s рассеянной волны лежит в плоскости, проходящей через ось z . Запишем уравнение Шрёдингера в цилиндрической системе координат ( r , φ , z ):

1 d f d

--1 r— r d r I dr

1 d ²

r ² д ф²

4 + k ² d z²

V (r, ф ,z ) = 0. (1)

В методе разделения переменных однозначные по ф решения (1) имеют вид

V n ( r, ф ,z ) = Z_n ( р ) e + i ^hz , n = 0, 1, 2, _,    (2)

где р = r^k ² - h ² , а Z_n - решение уравнения Бесселя

Рг ( ^rZ n 1+ ( р ² - п ²) Z n = 0.       (3)

dр^ dр )

Линейно-независимыми решениями уравнения (3) являются функции Бесселя первого и второго рода ( J_n и Y_n ) с целочисленными значениями индекса n . Значение величины h определяется из граничных условий на поверхности цилиндра. Используя разложение по собственным функциям и граничные условия на поверхности цилиндра, получим для падающей волны V i , внутренней волны V 1 и рассеянной волны V s выражения:

го

V , = Е ( - ^г ') J ( kr sin Z ) e' - kcos ^Z z ,         (4)

n = -ГО

V 1 = Е a n (-) J ( kr^m ² - cos ² Z ) e - kcos ^Z z , (5) n =-ro го

V s ( r, ф ,z ) = Е ( - ) ⁿ ( b n /2) H : ( kr sin Z ) е‘" ^ф - ^kcos ^{Z z} . (6) n =-ro

Здесь мы заменили коэффициент преломления n традиционным коэффициентом m , для того чтобы сохранить обычные обозначения и индексы в цилиндрических координатах для функции J_n и функции H_n ⁽¹⁾ , и ввели множитель

1/2 для удобства. Так как при упругом рассеянии число частиц сохраняется, то имеем

11 + b f = 1, b n = e ²*- 1, b n = b n

.

Здесь Sn - фазовый сдвиг. Амплитуда рассеяния f (ф) определяется из соотношения us = V, + Vs

^^^^^^B

f ( ф ) =

^ 2n k sin Z

I kr sin Z eⁱ⁽"^x x ^ f ( ф ) e ^,

r

Е ( - 1) ⁿ ( ь /2) е ™ ф - ™ ^{/4 - ik cos Z z} . (9) n =-ГО

Коэффициенты a_n и b_n находятся из граничных условий

V , ^{( R} ) ⁺ V s ^{( R} ) = V t ^{( R} ),

[ d / d r ( r • v , ( r ) + r • V s ( r ))] r = r = [ d / d r ( r • V t ( r ))] r = r .

Здесь R – это радиус цилиндра. Используя тождество

Jn-1 (x) Hn1 (x) - Jn (x)H n-1 (x) = 2 / ni x , можно получить a = Jn (x) НП!)( x) - Jn (x) Hn1»' (x) = n m * Jn (x') НП!)( x) - Jn (x') Hn1»' (x)

2 / n ix m * Jn (x') Hni)( x) - Jn (x') H^ (x)’ b = m * Jn (x') Jn (x) - Jn (x') Jn (x)

ⁿ   m * J n ( x ') H^( x ) - J n ( x ') H n ¹»' ( x )

.

В формулах (10), (11) и (12) введены обозначения x' = kRy/m ² - cos ² Z , x = kR sin Z ; штрих означает дифференцирование J_n и H_n ⁽¹⁾ по аргу-

ВЕСТНИК 2013 № 4

менту функции; m = x /x = mm - cos Z /sinZ, m2 = 1 -U/E = 1 -4пЕN ibi Ik2 - показатель преломления препятстiвия. Отметим, что, вычислив bn , можно определить дифференциальное сечение рассеяния на единицу длины цилиндра dф =

d ^ sc = | f | ² d ф =

2 n k sin Z

го

Е b n e”

-го

2 n k sin Z

го

- i ^π - ikr cos ζ e ⁴

2 π k sin ζ

ikr sin ζ e

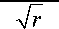
единицей длины прямого кругового цилиндра

радиуса R

da d^

2 n k sin Z

«

1 b 0 + ² Z b n cos n ^ | ² .

Рассмотрим эту же задачу в борновском приближении [7]. Потенциальная энергия – оптиче-

ский ядерный потенциал U – рассматривается как возмущение. Волновую функцию ищем в виде у = V о + V 1 , где V о = exp( i kr ) — соответствует падающей частице. В цилиндрической системе координат ( ρ , φ , z ) расходящаяся волна на больших расстояниях от оси имеет асимптотическое выражение функции Ганкеля первого рода, и поправка у 1 к волновой функции у ₀ на больших расстояниях от оси цилиндра R ₀ будет

V 1 =- ^m\u ( р ,z ) e kr • i n H 01) ( k p ) p d p d ф = 2 n h

приближения (20). Рассеиватель – это бесконечный круговой цилиндр радиуса R = 25 нм. Оптический ядерный потенциал для него U = 1,81эВ. Значение ядерного потенциала соответствует граничной скорости ОХН ν_гр = 5,90 м/с и граничной волне де Бройля λ_гр = 66,9 нм. На оптическом языке задачу можно сформулировать следующим образом: нейтронная плоская волна с длиной волны A v падает на цилиндр c показателем преломления n . Направление распространения нейтронной волны с осью цилиндра составляет угол Z = 90 o . Значения скорости ОХН v n и показателя преломления материала цилиндра n представлены в подписях к рисункам.

= f_B (Ф )

e ikR ₀

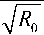
ВЕСТНИК 2013 № 4

отсюда амплитуда рассеяния

π i               2

me 4 h        — iqp fB (p) = -7T'^T I—(4nNb)e PdPd^ = h 22kk J 2m

= П ( Nb. ) e ⁿ² 2 J*n R 2 , [см" ² ]   ⁽¹⁷⁾

kc qR

где q = k _s - k i- вектор рассеяния, q = 2 k sin ф / 2. Тогда получим формулу для вычисления дифференциального сечения упругого рассеяния ОХН

d a _B d ф

= 2 П ( Nb ) ² Г k l

2 J 1 (2 k sin( ф /2) R ) Y

2 kR sin ф /2    J

в борновском приближении.

■ ( n R ² ) ² [см],

Обсуждение результатов численного моделирования

На рис. 1–3 приведены диаграммы рассеяния, вычисленные по формулам, полученным на основе решения уравнения Шрёдингера и формулам борновского приближения. Для вычисления коэффициентов b_n в (16) использовался алгоритм, изложенный в работах [10–11]. Время вычисления можно существенно сократить, если воспользоваться методами волновой теории катастроф [12–19]. На всех графиках по вертикальной оси отложены дифференциальные сечения рассеяния на единицу длины рассеивателя в логарифмическом масштабе (одно деление – 10 единиц), по горизонтальной оси – угол рассеяния (одно деление – 20 ^о ). Сплошная линия представ-

ляет результат вычисления дифференциального сечения рассеяния -^ по строгой формуле (16). Штриховая линия – по формуле борновского

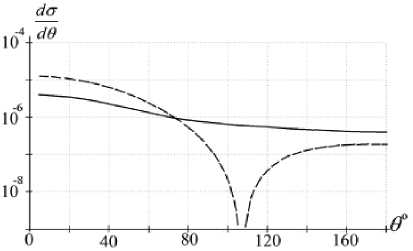
Рис. 1. Дифференциальные сечения рассеяния, вычисленные при скорости ОХН ν_n = 6 м/с. Значение показателя преломления n = 0,1771

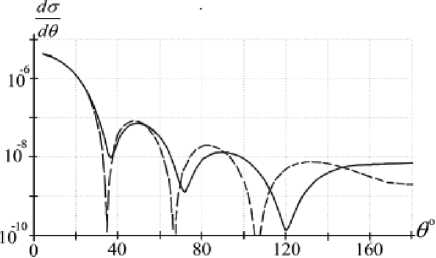
Рис. 2. Дифференциальные сечения рассеяния, вычисленные при скорости ОХН ν_n = 16 м/с. Значение показателя преломления n = 0,9294

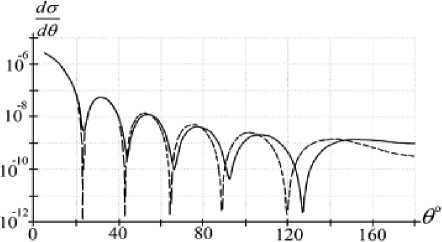
Рис. 3. Дифференциальные сечения рассеяния, вычисленные для скорости ОХН ν_n = 24 м/с. Значение показателя преломления n = 0,9693

В заключение отметим, что методика определения параметров неоднородностей (в частности, параметров углеродных нанотрубок) в наноструктурированных материалах основана на анализе экспериментальных данных по рассеянию очень холодных нейтронов при прохождении нейтронов через образец и математическом моделировании этого процесса. Сечения упругого рассеяния, необходимые для моделирования, вычисляются в первом борновском приближении. Для области значений энергии нейтронов (интервал энергий ОХН), в которых использование борновского приближения вызывает сомнения, сечения упругого рассеяния вычисляются на основе точного решения уравнения Шрёдингера методом разделения переменных для рассеивателей «правильных» форм (шары, цилиндры и др.).