Численное моделирование динамического поведения экспериментальной оснастки в среде ANSYS

1.    Техническая постановка задачи

Комплексные системы автоматического управления, содержащие насосы топливопитания двигателя, цифровые электронные регуляторы и резервную гидромеханическую часть [1], являются важными элементами летательных аппаратов.

Данные устройства испытывают существенные динамические нагрузки, поэтому проверка таких устройств в условиях, приближенных к реальным, является важной задачей.

В качестве объекта исследования был выбран цифровой электронный регулятор соответствующей серии, испытывающий в процессе эксплуатации повышенные динамические нагрузки, что было установлено во время приемо-сдаточных испытаний. Особенностью является то, что он находится под углом 16 градусов на двигателе энергетической установки и по условиям технической приемки испытания должны проводиться в условиях, максимально приближенных к реальным. Поэтому была предложена и разработана система оснастки, используемая при динамических испытаниях на вибропрочность и виброустойчивость. Один из вариантов подобных приспособлений представлен на рис. 1.

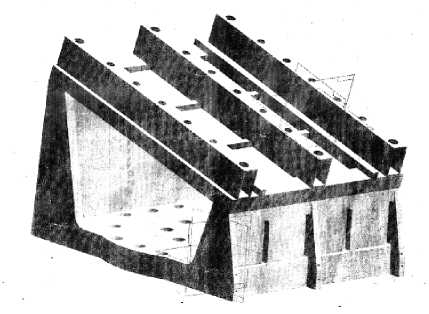
Рис. 1. Экспериментальная оснастка

В процессе эксперимента к верхней пластине оснастки с внутренней стороны в четырех точках крепится агрегат, также в четырех узлах располагаются датчики, отслеживающие частоту колебаний и виброускорение [2]. В заданном диапазоне частот 5-2000 Гц датчиками фиксируется наличие резонансов. На оснастке должны быть предусмотрены места для закрепления вибродатчиков, в непосредственной близости от мест крепления агрегата, а также место для крепления контрольного датчика, на котором фиксируется виброускорение, получаемое в процессе эксперимента.

Очевидно, что в процессе эксперимента, целью которого является установление резонансных режимов в заданном диапазоне, мы будем получать динамические характеристики не отдельного узла топливной аппаратура, а всей системы - оснастка плюс агрегат. Естественное желание - уменьшить это влияние. В связи с этим данная работа посвящена всестороннему исследованию динамических характеристик оснастки и выработке конструктивных изменений последней, для того чтобы ее частотный диапазон не совпадал с частотным диапазоном самого агрегата.

2.    Математическая постановка задачи

Анализ различных вариантов оснастки, используемой в динамических испытаниях, показывает, что при ее проектировании использованы канонические элементы типа пластин и балок. Для снижения веса используется перфорация. Поэтому, на наш взгляд, представляет интерес динамический анализ в нескольких вариантах. Один из них осно- вывается на использовании классических соотношений теории пластин и оболочек. Это возможно благодаря геометрии элементов и применению для оснастки традиционных материалов типа алюминий, сталь, титан и т.д. Другими словами, можно использовать соотношения теории пластин и оболочек, полученных на основе теории Кирхгофа-Лява. Если говорить об оснастке в целом как о системе, то это трехмерная конструкция, и в качестве второго варианта необходимо рассмотреть ее с точки зрения пространственного динамического поведения. Здесь удобно воспользоваться средой ANSYS. При этом необходимо предусмотреть сравнение результатов, полученных по первому и второму вариантам, причем использовать первый вариант как тестовую задачу.

Ниже приведены основные разрешающие соотношения с учетом гипотез Кирхгофа-Лява.

Геометрические соотношения

6 и      6 ² w 0

=--= — Z;г-

6X

6 V      6 2 W 0

=

6y6

= 0

6 и   6 V    _ 6 ² w ₀

Y xy =-- +-- = — 2 z-----

6y  6X

e xx

e e yy

e

(2.1)

Yxz = YVZ = 0 xz yz и физические соотношения

о

x

E

1 — ц ²

( e xx

+ ^ц • e yy )

E • z

^{1 -}ц ²

6 w

^ 6 X

+ ц •

2..,

6 ^w 0

J

о

y

E

1 ^-Ц ²

⁽ e yy

+ ц- e_xx ) =

E • z

^{1 -}ц ²

^w 2°

I 6 y

+ ц

^ww ⁰

6 X J

(2.2)

E 6 ² w₀

XZ          i Xy

1 + ц 6X 6y где Е - модуль упругости, G - модуль сдвига, р - коэффициент Пуассона. Все обозначения соответствуют принятым в [3].

Потенциальная энергия, накапливаемая элементарным объемом при упругой деформации пластинки, в соответствии с вышеназванными допущениями имеет следующее выражение:

dn = ¹ (а,- е_ + а • e _v +т -у„ ) dxdydz .            (2.3)

₂ x xx y yy xy xy

Принимаем, что пластинка совершает одно из главных колебаний, в этом случае ее прогиб определяется соотношением

W o ( x , y , z ) = w ( x , y ) • sin ( p • t + a ) .                 (2.4)

Для таких колебаний максимальные значения потенциальной и кинетической энергий будут иметь выражения:

Птах

= D л

22 w w (a x ²    a y ²

Т max

^ 2 p j j w ² dxdy

Тогда функционал примет вид

–

a ² w o a ² w o a x ² a y ²

( д2   A2

a w (^{a x a} y ^J

> dxdy

> . (2.5)

действие по Остроградскому-Гамильтону

⁵ ( T max

^^^^^^^.

П max ) = 0.

(2.6)

В результате подстановки в функционал T max , П_тах получается вариационное уравнение собственных форм поперечных колебаний пластинки:

jj D -^д ( s ) ⁽

2 У • ^ 2 W--p • W ^g

a

5 wds - □ M L — (5 w ) dl a n

+

(2.7)

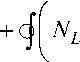
aHl ) --L 5wdl = 0, ai J

где M_L - изгибающий момент на контуре пластинки; N_L - поперечная сила на контуре пластинки; H_L - крутящий момент на контуре пластинки.

Если края пластинки жестко закреплены, то

( 6 w ) =sf^ w 1 = 0,                   (2.8)

L   кВn ) l если края пластинки свободны [3], то

N l - H = 0; M l = 0.               (2.9)

В l

3.    Анализ чувствительности

Как правило, для каждой собственной частоты существует хотя бы один параметр конструкции (геометрический, физический, конструктивный и т. д.), варьированием которого можно на нее влиять. Такие параметры называются чувствительными. С помощью их изменения можно переместить самые значимые резонансы за пределы исследуемой области.

Чувствительные параметры оказывают максимальное влияние на изменение собственных частот. Границы определения чувствительных и нечувствительных параметров зависят от поставленных целей и специфики решаемой задачи [4].

В результате исследования строятся функции чувствительности, определяющие количество резонансных пиков в зависимости от толщины верхней пластины, плотности материала и некоторых конструктивных особенностей, которые наглядно показывают, что и как нужно изменить в оснастке для уменьшения количества резонансных пиков в заданном диапазоне.

Приведенные выше соотношения для канонических элементов, таких как пластины, являются удобными, но реальная оснастка - сложная пространственная конструкция. Ее динамические характеристики могут оказаться отличными от динамических характеристик, которые были описаны ранее. Поэтому во втором варианте, оговоренном ранее, будем использовать численную процедуру метода конечных элементов. В данном случае удобна среда ANSYS, которая позволяет решать задачи любой сложности. Можно воспользоваться средой ANSYS как для пластин, так и для трехмерных конструкций, что дает возможность провести сравнение численных исследований с теоретическими результатами (первый вариант) и сформулировать практические рекомендации.

Сама оснастка изготовлена из материала Ал9М, а верхние ребра жесткости - стали 45х, характеристики приведены в табл. 1 [5].

Свойства материала оснастки

Таблица 1

Материал	Плотность, кг/м3	Модуль упругости, ГПа	Коэффициент Пуассона
Ал9М	2660	71	0,3
Сталь 45х	7826	200	0,26

Вынужденные пространственные колебания в эксперименте реализуются с помощью кинематического возбуждения, которое в нашем случае совпадает с осью Z. Самостоятельный интерес представляет динамическая реакция верхней части оснастки.

В качестве первой задачи рассмотрим динамическое поведение сплошной прямоугольной пластины. Теоретическое исследование проводится по методике В.С. Гонткевича [6], это один из немногих способов, который позволяет найти точное решение. Результаты теоретического исследования приведены в табл. 2.

В качестве граничных условий задается жесткое закрепление в двух противоположных краях, а остальные края свободны.

Частота собственных колебаний находится по формуле

® = kn! JD, f =   ,(3.1)

• a 2 m2

где ю - круговая частота (рад/с), f - частота колебаний (Гц), a - длина пластины (см), b - ширина пластины (см), h - высота пластины (см), E h ³

D - цилиндрическая жесткость (кгсм); D =т—.

12(1 -Ц 2)

Приведенная собственная частота колебаний пластинки вычисляется по формуле к2 = л2Х; X2 = С* + -4С,4 + 2—\yHH, + (1 -ц)J,J,],   (3.2)

где ц - коэффициент Пуассона [6].

При реализации принято: a = 42 см, b = 32 см, h = 2,5 см . Материал пластины Ал9М (см. табл. 1). Первые семь собственных частот колебаний пластины приведены в табл. 2.

Таблица 2

Теоретические значения собственных частот колебания пластины

Номер частоты	1	2	3	4	5	6	7
f, Гц	24,1	32,6	63,9	70,9	79,3	109,7	116,3

Выполняя необходимую процедуру тестирования и учитывая, что оснастка является трехмерной конструкцией, реализуем последовательность динамических задач в среде ANSYS. При этом будем оговаривать специфику реализации.

Граничные условия и свойства материала те же, что и в теоретическом исследовании.

Верхняя пластина оснастки имеет вид объемного тела, следовательно, разбиение производится 3D-элементами Solid.

В программном комплексе ANSYS используется несколько видов конечных элементов типа Solid. Выбирая готовые опции, заложенные в пакете ANSYS , получаем различные результаты. Иллюстрация данного эксперимента приведена на рис. 2.

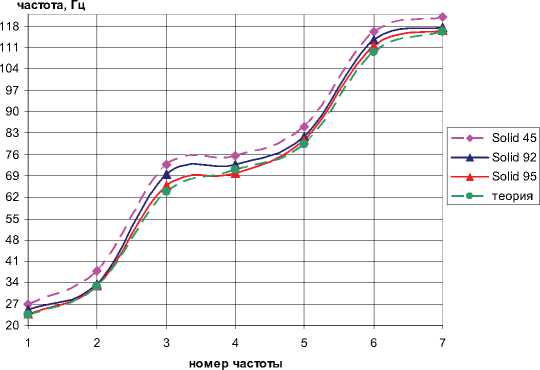
Рис. 2. Сравнение собственных частот колебаний пластины в зависимости от вида конечного элемента

Проведенный модальный анализ показывает, что практически все выбранные элементы дают хороший результат, однако элемент Solid 95 дает значения собственных частот, более близкие к теоретическим. Поэтому в дальнейших расчетах будем использовать указанный выше элемент дискретизации. Он является квадратичной версией объемного (3D) элемента и в состоянии использовать нерегулярную форму сетки без потери точности. Элемент Solid 95 имеет совместные формы перемещений и описывает модели с искривленными границами. Элемент определяется 20 узлами, имеющими три степени свободы в каждом: перемещения в направлении осей X, Y и Z узловой системы координат.

Геометрия, расположение узлов и система координат элемента, показана на рис. 3.

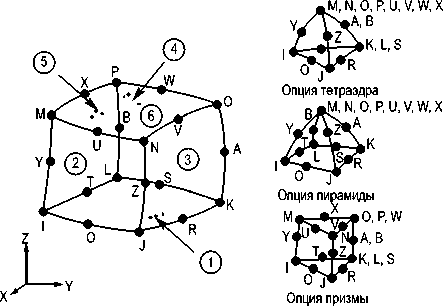
Рис. 3. Геометрия конечного элемента Solid 95

Так же при разбиении можно варьировать размеры конечных элементов, всего в ANSYS предусмотрено десять автоматических режимов разбиения, отличающихся величиной элементов. Проведен модальный анализ пластины, разбитой конечными элементами Solid 95 разной величины (рис. 4).

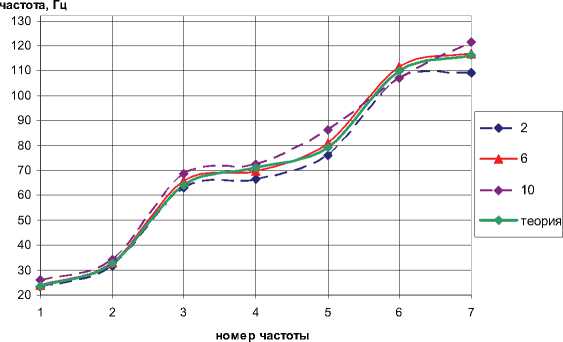
Рис. 4. Графическое сравнение собственных частот колебаний в зависимости от режима разбиения

Из рис. 4 видно, что к теоретическим значениям наиболее близок шестой режим разбиения.

Следовательно, в дальнейших расчетах будет использоваться разбиение конструкции элементом Solid 95 в шестом режиме.

Точность решения определяется шагом интегрирования: чем меньше шаг, тем выше точность. Использование процедуры автоматического выбора шага дает возможность программе менять его величину в процессе решения в зависимости от частоты отклика и влияния нелинейностей, что уменьшает общее число шагов и сберегает ресурсы компьютера [7]. В дальнейшем все результаты получены при автоматическом шаге.

Рассматриваемая пластина имеет более простой вид по сравнению с реальной (рис. 5). В процентном соотношении их различие по массе составляет около 5 %.

Рис. 5. Упрощенная и реальная пластины

Проведем модальный анализ этих двух пластин и сравнение их собственных частот и форм колебаний (рис. 6).

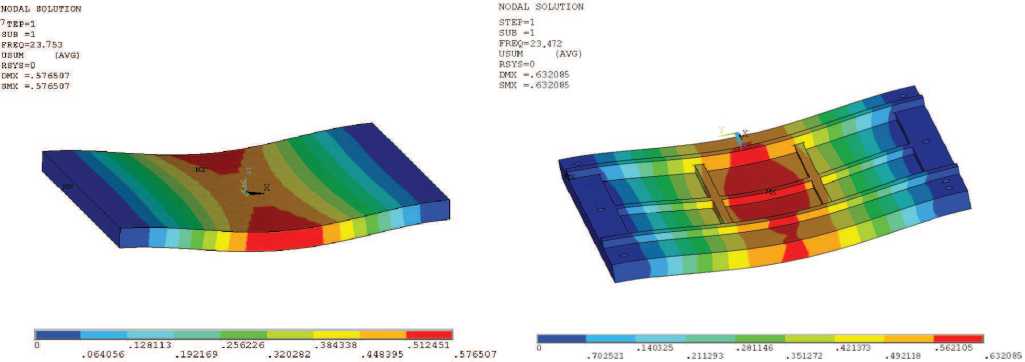
Рис. 6. Первая форма колебаний упрощенной и реальной пластин

Из рис. 6 видно, что различия в частотах и формах колебаний рассматриваемой и реальной пластин несущественные. Поэтому в дальнейшем при исследовании конструкции будет использована упрощенная модель пластинки.

Модальный анализ в среде ANSYS позволяет установить параметры колебаний конструкций, с его помощью определяются собственные частоты и формы колебаний. Кроме того, он используется как отправная точка для других, более подробных динамических расчетов, таких как нестационарный динамический анализ или отклик системы на гармоническое воздействие [8].

В результате модального анализа получается спектр собственных частот колебаний оснастки. В интервале 5-2000 Гц находится большое количество этих частот. При частотах до 170 Гц колебания происходят за счет верхней пластины. Колебания тонких боковых ребер происходят на более высоких частотах - 170-1000 Гц, при частотах более 1000 Гц колеблется конструкция в целом.

В качестве вариантного исследования был проведен модальный анализ оснастки с добавлением боковых ребер и верхних ребер жесткости двух видов из материала сталь 45х (табл. 3).

Таблица 3

Собственные частоты колебания конструкции в зависимости от конструктивных особенностей

Номер частоты	m = 31,32 кг	m = 31,65 кг	m = 32,76 кг	m = 35,64 кг
	Частоты, Гц
1	22,3	22,5	24,3	23,8
2	31,6	31,5	37,4	39,1
3	34,8	34,4	40,2	42,1
4	51,7	51,8	50,8	49,5
5	65,9	65,5	67,1	61,6

Анализ результатов показал, что добавление различных ребер жесткости не оказывает существенного влияния на собственные частоты колебания конструкции. Поэтому выполним конструктивные изменения других жесткостных элементов оснастки. В середине верхней пластины делается абсолютно жесткая подпорка, что в пакете ANSYS выглядит как защемление центрального узла, то же самое - в четырех узлах, далее крепится ребро жесткости посредине конструкции в продольном направлении, что в программе реализуется как защемление ее по средней линии. Результаты численного эксперимента сведены в табл. 4.

Таблица 4

Собственные частоты колебания конструкции в зависимости от добавления жестких элементов разного рода

Номер частоты	Защемление верхней пластины в одной точке	Защемление верхней пластины в четырех точках	Защемление оснастки по средней линии
	Частоты, Гц
1	35,7	47,1	36,7
2	39,5	57,5	45,4
3	45,9	73,1	83,5
4	61,1	79,4	87,1
5	66,8	88,3	104,9

Как видно из табл. 4, защемление нескольких узлов верхней пластины приводит к большему увеличению значений частот по сравнению с добавлением ребер.

Одним из вариантов конструктивных изменений оснастки является варьирование свойств материала, что было сделано в расчетах, а результаты сведены в табл. 5.

Таблица 5

Собственные частоты колебания конструкции в зависимости от вида материала

Номер частоты
	Оснастка из Ал9М m = 32,76 кг	Оснастка - Ал9М, верхние ребра жесткости - сталь 45х m = 34,48 кг	Оснастка из стали 45х m = 96,38 кг
Частоты в зависимости от вида материала, Гц
1	24,3	24,3	23,7
2	37,4	37,4	36,4
28	189,6	188,1	185,8

Окончание табл. 5

Номер частоты	Оснастка из Ал9М m = 32,76 кг	Оснастка - Ал9М, верхние ребра жесткости - сталь 45х m = 34,48 кг	Оснастка из стали 45х m = 96,38 кг
29	193,9	188,9	198,8
43	242,4	239,4	237,7
44	247,5	247,4	241,7

При использовании стали масса оснастки существенно увеличивается, что приводит к уменьшению значений частот.

Для определения наиболее значимых частот (тех, при которых амплитуда имеет наибольшее значение) проводится гармонический анализ. Этот вид анализа гораздо более сложен, чем модальный, поэтому, вообще говоря, необходимо предварительное выполнение анализа работой по изучению физики проблемы, что может существенно сократить затраты инженерного труда и компьютерные ресурсы. Такая работа может состоять из следующих этапов:

• -    анализ более простых моделей (во многих случаях расчетные модели из пружин, масс и балок оказываются достаточными для получения динамического отклика сложной конструкции);

• -    проведение статического анализа перед введением нелинейностей (иногда можно убедиться, что в учете нелинейности нет необходимости);

• -    выполнение модального анализа для оценки реакции системы и определения шага решения по времени.

На интервале частот в пределах от 5 до 2000 Гц, получаются амплитудо-частотные характеристики оснастки (рис. 7, 8) в четырех точках крепления датчиков (рис. 9).

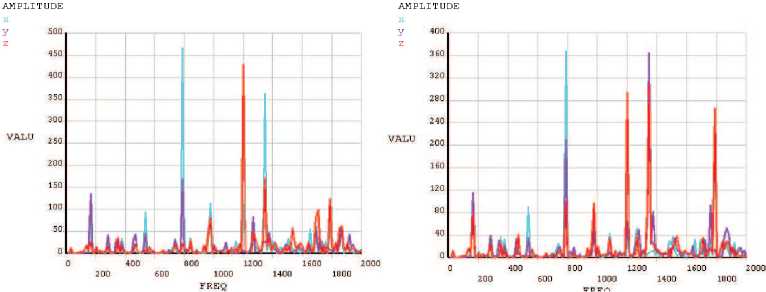
Рис. 7. Амплитудо-частотная характеристика конструкции в 1-й и 2-й точках

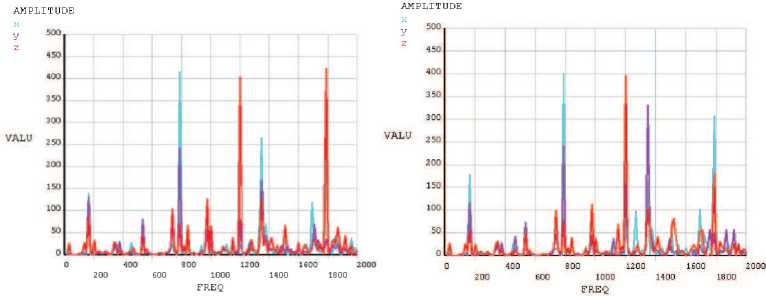
Рис. 8. Амплитудо-частотная характеристика конструкции в 3-й и 4-й точках

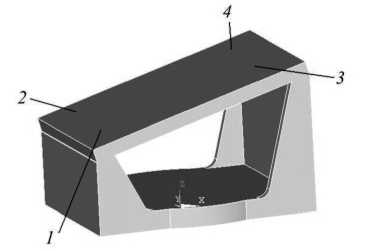
Рис. 9. 1, 2, 3, 4-я точки крепления датчиков

При сопоставлении полученных амплитудо-частотных характеристик с экспериментальными данными (результаты разработчика оборудования и оснастки) получаются количественные и качественные совпадения.

Из всех геометрических параметров конструкции можно варьировать только толщиной верхней пластины, так как все остальные размеры имеют определенные значения, которые изменять нельзя. От 5 до 1000 Гц колебания оснастки в основном происходят за счет пластины, поэтому данный анализ проводится в этом диапазоне. Начальная ее толщина 25 мм, при постепенном увеличении получается набор амплитудо-частотных характеристик.

С помощью метода наименьших квадратов [9] по полученным точкам строится функция чувствительности к изменению геометрических параметров.

Получается полиномиальная функция, точность которой составляет 97-99 % (рис. 10, 11).

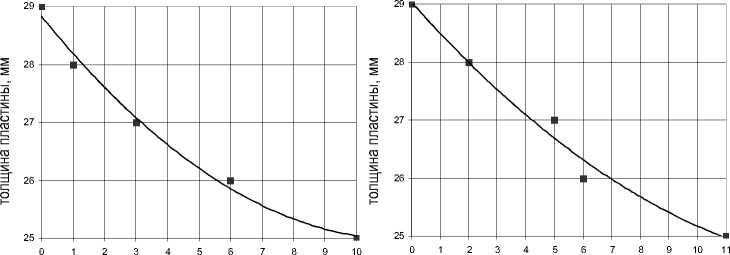
количество резонансов      R 2 = 0.9⁹⁰⁷                    количество резонансов      R 2 = 0.9⁷⁹⁹

Рис. 10. Функция чувствительности к изменению геометрических параметров в 1-й и 2-й точках

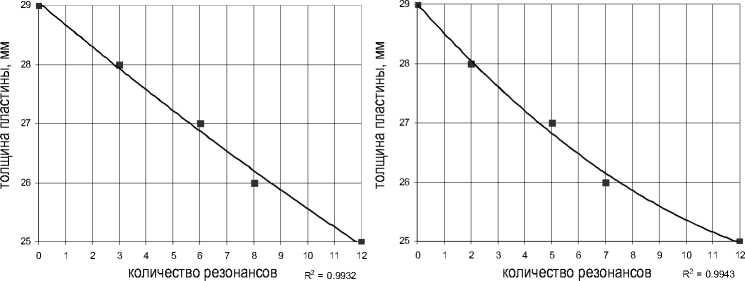
Рис. 11. Функция чувствительности к изменению геометрических параметров в 3-й и 4-й точках

При задании толщины верхней пластины свыше 29 мм происходит значительное увеличение массы оснастки и дальнейшее ее варьирование теряет свою эффективность. Для того чтобы уйти от резонансных режимов на диапазоне частот 5-1000 Гц нужно увеличить толщину верхней пластины оснастки с 25 мм до 29 мм.

Рассмотрим более жесткие материалы оснастки, их свойства приведены в табл. 6.

Таблица 6 Свойства используемых материалов оснастки

Материал	Плотность, кг/м3	Модуль упругости, ГПа	Коэффициент Пуассона
Ал9М	2660	71	0,3
Сталь 45х	7826	200	0,26
Титан	4505	112	0,32
Бронза	8800	110	0,35

С помощью метода наименьших квадратов строится функция чувствительности к изменению физических параметров (это степенная функция) с точностью 88-98 % (рис. 12, 13).

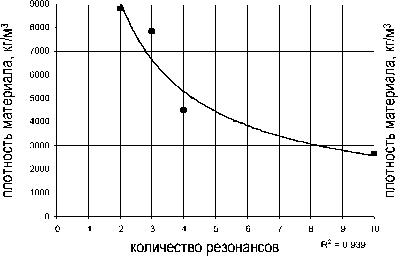
Рис. 12. Функция чувствительности к изменению физических параметров в 1-й и 2-й точках

0     1     2     3     4     5     6     7     8     9     10    11

количество резонансов      R² = 0.9⁷⁶⁶

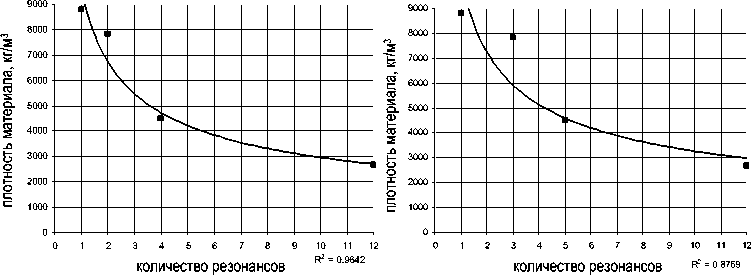
Рис. 13. Функция чувствительности к изменению физических параметров в 3-й и 4-й точках

Для того чтобы уйти от резонансных режимов на диапазоне частот 5-1000 Гц оснастку нужно изготавливать из материалов с более высокой плотностью. Учитывая исходные материалы проектировщиков, было рекомендовано заменить алюминий.

Проведем также анализ чувствительности оснастки с добавлением боковых ребер и верхних ребер жесткости из материала АЛ9М. Из полученных результатов видно, что это не приводит к значительным изменениям амплитудо-частотных характеристик, то есть не является эффективным.

Выводы

• 1.    Проведено численное моделирование динамического поведения реальной экспериментальной оснастки, используемой в динамических испытаниях топливной аппаратуры.

• 2.    Установлены частотные диапазоны, содержащие резонансные режимы оснастки, и проведено их сравнение с соответствующими динамическими режимами испытуемого объекта.

• 3.    Детально изучено влияние параметров оснастки (материал, геометрия, конструктивная жесткость) на амплитудо-частотные характеристики. Результаты представлены в виде функций чувствительности.

• 4.    Выполнено всестороннее тестирование используемых при численном моделировании опций среды ANSYS.

• 5.    Предложены технические и конструктивные решения для применения в инженерной практике при проведении динамических экспериментов.