Численное моделирование динамики ионосферно-плазмосферного обмена в спокойных и возмущенных условиях

Потребности теоретического описания процессов и явлений в околоземной космической плазме средствами математического моделирования возникают при решении прикладных задач в области радионавигации, радиосвязи, практической космонавтики, экологии, метеорологии.

Исследована динамика плазмы среднеширотной ионосферы и плазмосферы в спокойных и возмущенных условиях.

Ишанов Сергей Александрович доктор физико-математических наук, профессор, профессор Института высоких технологий. Балтийский федеральный университет имени Иммануила Канта, Калининград. Сфера научных интересов: математическое моделирование, численные методы и комплексы программ. Автор более 150 опубликованных научных работ.

Численное моделирование динамики ионосферно-плазмосферного обмена ...

ной плазмы, кинетики сверхтепловых электронов, электрического дрейфа, ионосферно-плазмосферного взаимодействия и химической кинетики.

Используемая в данной работе математическая модель системы «ионосфера – плазмосфера», основанная на системе уравнений магнитной гидродинамики, включает элек- троны и положительные ионы: O +, H +, He +, N+, N +, NO +, O+, H2O +, OH +, метастабильные

O 2 ( 1 A q ) , O ( ¹ D ) , N ( ² D )

и малые компоненты с полным учетом их динамики, что позволя- ет корректно описывать околоземную плазму в интервале высот от нижней границы

F -области до нескольких радиусов Земли в различных геофизических ситуациях.

Представлены полученные при численном моделировании среднеширотной ионосферы и плазмосферы результаты вычислительных экспериментов в естественных условиях и условиях техногенных воздействий.

Математическая модель и вычислительные методы

Полагаем, что макроскопическое движение плазмы происходит вдоль геомагнитного поля. Выбором дипольной системы координат сведем физическую задачу трехмерного движения плазмы к двумерной математической задаче в переменных s (координата вдоль силовой линии) и t (время).

Математическая модель основана на численном решении системы уравнений гидродинамики частично ионизированной плазмы для ионов и электронов. Система уравнений непрерывности, импульса и теплового баланса для заряженных компонентов может быть записана в следующем виде [5; 8]:

a n i    1 ^{д (} An i v i )

1---= Ч, - Li, дt A    д5        i i nimi

' д v,д v

L + vii- д t

д P i

+--= -nm^ sin I + д5       '

n i ^д P e

N e д 5 ’

⁺ n i ^ ^Sij ⁽ v j - v i ) ⁺ n i R i ⁽ v nx cos I - v i ) - j = 1

³ kn

2 ⁱ

' д T     д ТЛ р,	д ( Av i )	1 д (	д Т )	(3)
+ v   i- +	-	—	A ^ i^T" 1 = P ie + P in + P ij , д 5 )
ч д t     i д 5 ) A	д 5	A д 5 1
д Т     д T ) рЕ —- + и,—- +—	д ( AU e )	1 д	д Т)	(4)
		—	1 A ^ e — 1 = P g + P ei - P en ,
e	д 5	A д 5	l       д 5 ) g

где индекс n в величинах v_nx , P_in , P_en связывает их с нейтральными частицами; индекс e в величинах N e , p e , P ie , T e , u e , X _e , P_ei , P en - с электронами; u e - скорость электронов; n_i , m_i , v_i , T_i – концентрация, масса, скорость и температура ионов i -го сорта соответственно ( i = 1 ^ O ⁺ , i = 2 ^ H ⁺ , i = 3 ^ O ₂ ⁺ , i = 4 ^ NO ⁺ , i = 5 ^ N ₂ ⁺ ) ; 5 - координата вдоль геомагнитной силовой линии, положительная в направлении от Северного полюса к Южному; A – расходимость силовых линий магнитного поля; I – магнитное наклонение; g – ускорение силы тяжести; v_nx – меридиональный компонент скорости нейтрального ветра; L_i , Q_i – коэффициент рекомбинации и функция ионизации ионов сорта i ; N_e – электронная концентрация; p_i – давление ионного газа, состоящего из частиц i -го сорта;

pe - давление электронного газа; Te - электронная температура; Ae, Ai - коэффициенты теплопроводности электронного и ионного газов соответственно; k – постоянная Больцмана; Ri – коэффициент силы трения между ионами i -го сорта и нейтральными части- цами; Sij – коэффициенты силы трения между ионами i -го и j -го сортов; Pg – скорость нагрева тепловых электронов сверхтепловыми фотоэлектронами; Pei – скорость теплообмена электронов с ионами; Pie – скорость теплообмена i -го иона с электронами; Pij – скорость теплообмена i -го иона с ионами j -го сорта; Pin – скорость теплообмена i -го иона с нейтралами; Pen – скорость охлаждения электронов на нейтральных частицах.

Положим справедливым условие квазинейтр и. = — f ■ N e „

альности плазмы n i v i .

Химические реакции, определяющие кинетику ионов, а также образующихся в резуль- тате их взаимодействия с нейтральными компонентами молекулярных ионов, представлены в [2; 5; 6; 9].

Реакции резонансной перезарядки, влияющие на существование плазмосферы Земли, имеют следующие коэффициенты [13]:

O + + H ^ H ⁺+ O , к₁₂ = 2.5 - 10 ¹¹ V T ;

H ++ O ^ O ++ H, к 21 = 2.2-10 11 VT , где T – эффективная температура.

Члены Pei,Pin,Pie,Pen,Pij , входящие в уравнения теплового баланса (3), (4), которые учитывают упругие и неупругие процессы обмена энергией между заряженными частицами и нейтральными составляющими, взяты из [2]. Учет взаимодействия плазмы с горизонтальным термосферным ветром на ионосферных высотах проводится так же, как в [5]. Для расчета Pg согласно [4] решалось кинетическое уравнение для сверхтепловых электронов. Нестационарные уравнения фотохимического равновесия для молекулярных ио- нов O2+, NO +, N2+ записываются в виде

V = Q i - «i n i , i = 3,4,5. d t

Численное решение системы уравнений модели осуществлялось вдоль геомагнитной силовой линии с применением метода конечных разностей. Линеаризация разностных уравнений проводилась с использованием значений неизвестных функций, взятых с пре- дыдущего временного слоя, с последующими итерациями по нелинейности и связанности уравнений. При решении системы уравнений (1), (2) использован подход, приведенный в [3; 7; 11]. Сначала запишем уравнение (2) в дивергентной форме [5]:

^d n i v i + £ ^d An i v i² + 8 P i = F d t    A d s       d s     i .

Здесь F_i учитывает действие внешних сил:

F i = n i Y i ⁺ v i ( Q i ^{- a} i n i ),

Y i =^- g sin I ⁺ - ^{i L (} v j ^- v i ) ⁺ R i" ⁽ v nx cos I ^- v i )-- 1— ^ p e" .

m i            m i                 m i N e d s

Численное моделирование динамики ионосферно-плазмосферного обмена ...

Используя метод суммарной аппроксимации [7; 11], можно разделить исходную систему уравнений на последовательно решаемую систему уравнений переноса дni + 1 дAnivi _ о; dnivi + 1 dAnivi2 + dpi _ ^ д t A д s      ’ д t A дs дs

и систему обыкновенных дифференциальных уравнений, учитывающих элементарные процессы (фотохимию и столкновения)

dndv

— + «ini _ Qi;    - + Дv _ fi, dtdt где pi и fi учитывают силы взаимодействия (сила тяжести, электрическая сила, силы трения ион – ион, ион – нейтрал):

S

в _—+—; f. _ Yi + PiVi.

mimi

Решение уравнений (8) дается формулами

П, _ne-™‘ + ^-(1 -eai ); Vt _ve~тв + Ь-(1 -e""^i), i i            ai'                    i i ^i где ni,vi – концентрация и скорость, полученные решением системы (7); nˆi,vˆi – результирующие значения концентрации и скорости, полученные за два шага: перенос + элементарные взаимодействия.

Для решения системы уравнений переноса (7) применялся алгоритм, основанный на явной консервативной схеме [3; 11].

Результаты численного моделирования

Для расчета пространственно-временных вариаций концентраций и температуры нейтральных компонентов O , H , N , N ₂, O ₂, He используется модель MSIS [12].

Пространственно-временное распределение нейтральных компонентов H ₂ O , H рассчитывалось так же, как в работе [6]. В некоторый момент времени включается инжектируемый компонент H ₂ O , который учитывается при решении уравнения диффузии для атомарного водорода как дополнительный химический источник.

В качестве модельной задачи был выбран расчет суточных вариаций ключевых параме-трое ионосферы для геомагнитной трубки с параметром Макилвейна L _ 2 (наибольшая высота над поверхностью Земли 6356 км) для средней геомагнитной солнечной активности (индексы K_p _ 3, Г ₁₀ .7 _ 150) и начала года в Южном (лето) и в Северном (зима) полушариях, а также для равноденствия.

Рассмотрим суточные вариации структурных параметров максимума слоя F 2.

На Рисунке 1 показан суточных ход h_mF 2, N_mF 2 в Северном полушарии при инжекции H ₂ O для зимних условий (начало воздействия LT _ 12 ч), начало возмущения ионосферы Южного полушария LT _ 12,13 ч.

Значения N_mF 2 для локального несопряженного выброса в Северном полушарии в сравнении с фоном уменьшились на 30 % (интервал времени 0…6 ч), а для разнесенных по пространству и времени воздействий – примерно в 2 раза.

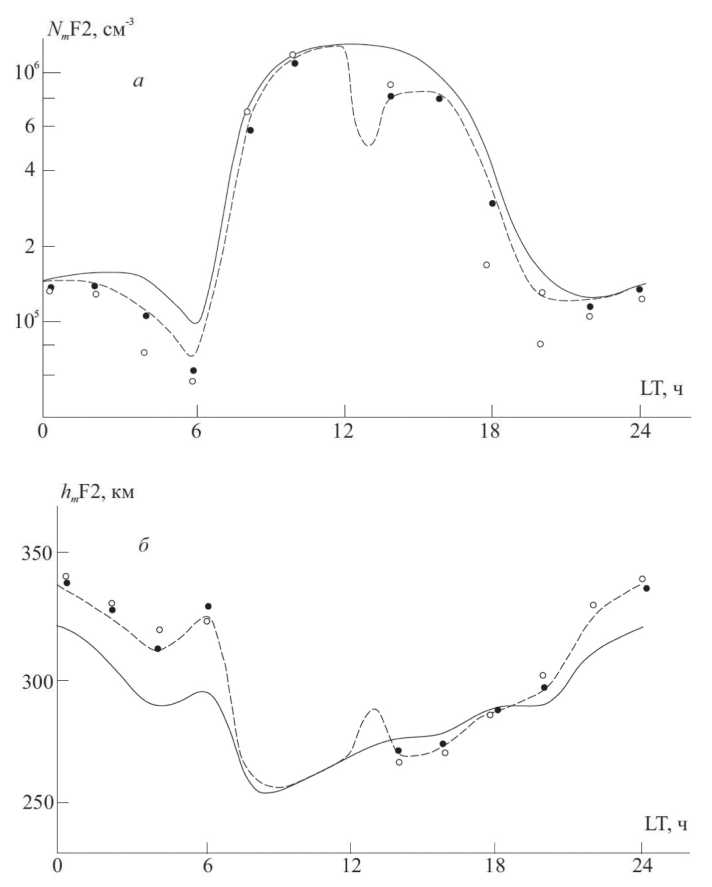
Рисунок 1. Суточные вариации N_m F2 (а), h_m F2 (b) в Северном полушарии. Сплошные линии – профили, соответствующие невозмущенным условиями, штриховые – локальное несопряженное воздействие с 12.00 LT; темные точки – техногенное возмущение в Северном и Южном полушариях (12.00 LT), светлые – воздействие в Северном (12.00 LT) и Южном (13.00 LT) полушариях

Для Южного полушария наблюдается подобное поведение структурных параметров

N_mF 2, h_mF 2 . Это можно объяснить тем, что в случае сопряженных возмущений плазмосфера сильнее обедняется, и в ночное время это обеднение проявляется наиболее заметно.

Соответствующие этому модельному сценарию плазменные потоки заметно меняют свою величину (см. Рисунки 2, 3).

Спустя 3 часа в Южном полушарии ионный поток, направленный в Северное полушарие (см. Рисунок 2) в случае сопряженных возмущений (в Южном полушарии 13.00 LT, в Северном полушарии 12.00 LT) меняет свою величину в 5…6 раз по сравнению с локальным возмущением только в одном полушарии.

Для возмущений, отличающихся временным сдвигом, наблюдается заметное расхождение в потоках плазмы в сравнении с фоновым случаем (см. Рисунок 3).

Расчеты суточных вариаций h_m F 2, N_m F 2 для условий весеннего равноденствия при различных сценариях техногенного воздействия показывают, что ввиду известной симметрии заметного эффекта взаимодействия магнитосопряженных областей в этом случае получить не удается.

Численное моделирование динамики ионосферно-плазмосферного обмена ...

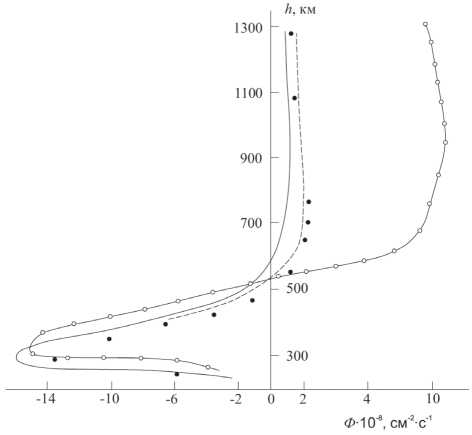
Рисунок 2. Высотные профили ионных потоков в Южном полушарии в 15.00 LT. Линия со светлыми точками соответствует сопряженным выбросам в Северном (12.00 LT) и Южном (13.00 LT) полушариях. Другие обозначение те же, что на Рисунке 1

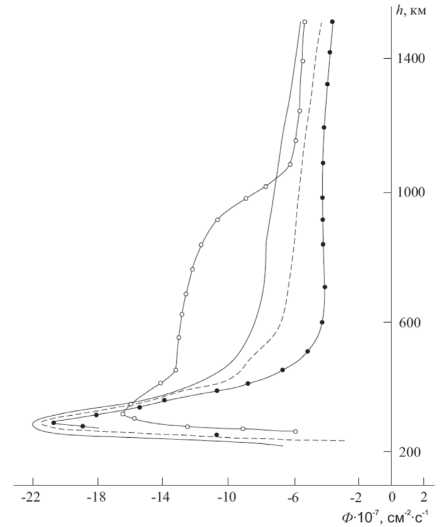
Рисунок 3. Высотные профили ионных потоков в Северном полушарии в 04.00 LT. Линия с темные точками – одновременные (12.00 LT) сопряженные выбросы. Другие обозначения те же, что на Рисунках 1 и 2

Анализируя характер пространственных вариаций полного потока плазмы, можно заключить, что, например, техногенное возмущение в Северном полушарии в полдень, а в Южном – в 13.00 ч приводит к увеличению примерно в 2,5 раза потока из Северного полушария в Южное ( LT = 15 ч) по сравнению с несопряженным локальным возмущением.

Поведение концентрации электронов в максимуме и высоты максимума слоя F 2 в случае аналогичного ночного воздействия приведено для двух полушарий на Рисунках 4, 5.

WJ2, см'1

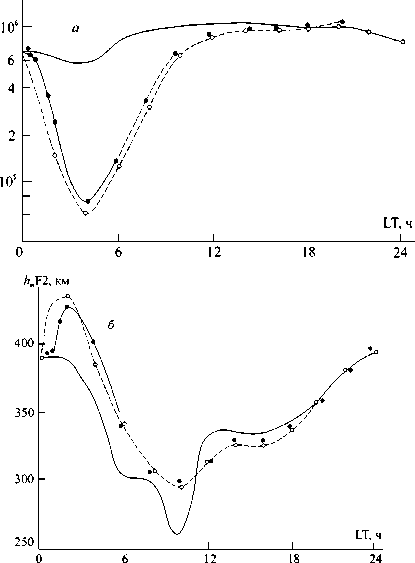
Рисунок 4. Суточные вариации N_m F2 (а), h_m F2 (б) в Южном полушарии. Линии со светлыми точками – сопряженные техногенные воздействия в 00.00 LT, с темными – воздействие в Северном (00.00 LT) и Южном (01.00 LT) полушариях; сплошные линии – в невозмущенных условиях

В случае одновременного возмущения магнитосопряженных ионосфер в полночь величина N_mF 2 отличается от соответствующей величины для несопряженного воздействия в 1,5 раза на интервале LT = 4…6.

Для случая техногенного воздействия на ионосферу Южного полушария со сдвигом на 1 ч 01.00 LT ввиду известной инерционности плазмосферы этот эффект меньше.

Необходимо отметить, что при околополуночных воздействиях увеличивается существенно электронная температура: несопряженное возмущение по отношению к фону повышает температуру ионосферной плазмы в среднем на 500 К, а сопряженные инжекции H₂O – на 1300 К.

Ионосферно-плазмосферный обмен при разнесенных по пространству и времени техногенных возмущениях проявляется в заметных изменениях потоков плазмы из сопря-

Численное моделирование динамики ионосферно-плазмосферного обмена ...

женных областей и долговременных изменениях электронных концентраций в области главного ионосферного максимума.

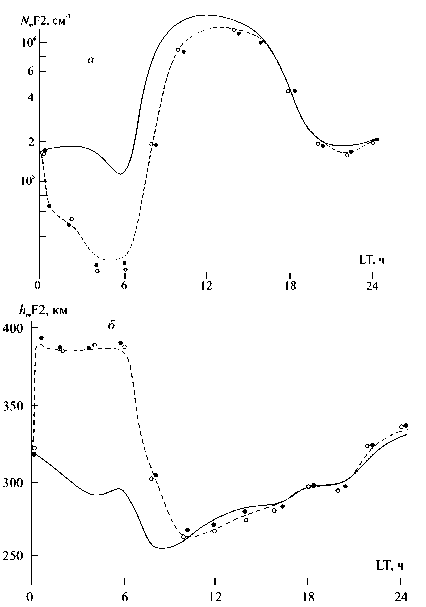
Рисунок 5. Суточные вариации N_m F2 (а), h_m F2 (б) в Северном полушарии. Сплошные кривые – невозмущенные условия, штриховые – «локальное» несопряженное воздействие с 00.00 LT; светлые точки – одновременное (00.00 LT) антропогенное возмущение в сопряженных ионосферах, темные – воздействие в Северном (00.00 LT) и Южном (01.00 LT) полушариях

Заключение

На основе гидродинамической усовершенствованной модели динамики тепловой плазмы в геомагнитных силовых трубках исследованы процессы переноса плазмы и энергии в ионосфере и плазмосфере Земли в различных геофизических условиях.

Численное исследование показало, что корректная постановка задачи моделирования физико-химических процессов в околоземной космической плазме формулируется для полной системы уравнений движения и непрерывности гиперболического типа.

В результате численного моделирования получены и проанализированы пространственно-временные распределения макроскопических параметров ионосферно-плазмос-ферной плазмы в спокойных и возмущенных условиях.

Показано, что динамика ионосферно-плазмосферного взаимодействия при техногенных возмущениях сопряженных ионосфер проявляется в заметном увеличении плазменной температуры, существенных изменениях структуры F области и ионных потоков из магнитосопряженных областей.