Численное моделирование динамики испаряющейся многофракционной парокапельной смеси метана в трубе с учетом закрутки потока

Различные процессы в промышленной энергетике связаны с течениями газов и жидкостей. В связи с этим задачи экспериментального, теоретического и численного исследования гидродинамических процессов имеют актуальность для конструирования и оптимизации технологий промышленной энергетики. Для многих задач классической гидродинамики получены точные решения, которые возможно использовать в практических приложениях. Но в ряде случаев возникает необходимость моделирования течений сред в отличие от классической гидродинамики, не являющихся однородными и включающих в себя две и более компоненты. Неоднородные среды могут содержать компоненты с различными агрегатными состояниями, в этом случае такие среды именуются многофазными [1–3]. Одним из видов многофазных сред являются аэрозоли – смесь газа и жидких капель или твердых частиц [2]. В этом случае кроме механических эффектов в течениях могут протекать термодинамические процессы – например, испарение капель. В данной работе рассматривается динамика парокапельной среды с испаряющимися каплями. Течения парокапельных смесей с испарением дисперсной фазы протекают в аппаратах, предназначенных для подогрева газожидкостных смесей [4] в технологиях промышленной энергетики, работающих со сжиженным природным газом. В работе [5] с помощью численных методов моделировалось течение газа с дисперсными частицами. Необходимость исследования связана с проблемами течения запыленных сред в проточных элементах газотурбинных двигателей летательных аппаратов. Движение двухфазной смеси описывалось в плоском нестационарном случае с учетом вязкости несущей среды и взаимодействия несущей среды и дисперсной фазы. В публикации [6] описан численный алгоритм, предназначенный для расчетов течений смеси, в рамках односкоростного подхода, на криволинейных сетках, проведен анализ уравнений математической модели. Исследование [7] посвящено разработке математической модели двухфазного течения, учитывающей эффекты дробления и испарения капель жидкости в потоке газокапельной среды. В работе разработана математическая модель и проведены численные расчеты процессов испарения и механического разрушения капель жидкости как в дозвуковых, так и в сверхзвуковых потоках. В публикации [8] в автомодельной постановке получено решение для процесса диффузионного перемешивания аэрозоля с газом при одномерной геометрии моделируемого процесса. Особенностью модели является учет фазовых переходов. Исследованы температурные и концентрационные поля при моделировании различных первоначальных температур газа и дисперсной фазы. Также рассмотрены различные парциальные плотности пара в газе. Анализировались типы перемешивания аэрозоля с газом, имеющим различные температуры, а также моделировалось перемешивание с перегретым паром. В работе [9] численно моделировался процесс распространения дисперсной примеси и теплообмен в закрученном газокапельном потоке, движущемся за расширением трубы. Газовая фаза описана трехмерной системой уравнений Навье – Стокса, осредненной по Рейнольдсу, с учетом обратного влияния частиц на динамику несущей фазы. Эйлерово и лагранжево описания дают качественно близкие результаты для мелкодисперсных капель (d ≤ 30 мкм), при этом для самых крупных, исследованных в данной работе частиц (d = 100 мкм), отличие в результатах расчетов является существенным. В работе [10] представлена численная модель и результаты расчетов межфазного тепломассообмена в двухфазном потоке, создаваемом при форсуночном распы-ливании жидкости в газ. В качестве основы предлагаемой математической модели использованы нестационарные дифференциальные уравнения течения сжимаемой среды, дополненные уравнениями тепло- и массопередачи от капель к газу. Для интегрирования уравнений динамики двухфазной среды использована явная схема Лакса – Вендроффа. В публикации [11] с помощью анализа экспериментальных данных по газификации кислорода на стационарной установке газификации выполнена идентификация дифференциальной параметрической модели теплообмена в газификаторах закрытого типа. Разработаны методики оптимизации работы газификатора по достижению заданного диапазона выходной температуры в ста- ционарном и нестационарном режимах работы. В статье [12] рассматривается процесс газификации угольной пыли в потоке дутья с высоким содержанием кислорода. С помощью математической модели в одномерном стационарном приближении исследуется изменение характеристик процесса при добавлении к кислородному дутью диоксида углерода и смеси диоксида углерода и водяного пара. Расчеты показывают, что добавление диоксида углерода позволяет снизить удельные затраты кислорода на газификацию и повысить полноту конверсии топлива. В публикации [13] численно моделируется деформация границы раздела «газ – жидкость» на ранних стадиях разрушения столба вязкой жидкости, для математического описания процесса численно интегрируется совокупность из двух систем уравнений Навье – Стокса для моделирования двухкомпонентной смеси. В работе [14] проведены исследования гидродинамических и тепловых эффектов в турбулентных течениях однородной воды, однородного этиленгликоля и водно-этиленгликолевой смеси с твердыми частицами оксида алюминия. Было проанализировано влияние различных жидкостей – несущих сред и различных объемных долей твердых частиц для течений с числами Рейнольдса в диапазоне от 5000 до 50 000. Поля потока жидкости и температуры были смоделированы с использованием коммерческого программного обеспечения CFD FLUENT.

В публикации [15] с помощью проведения ряда физических экспериментов изучены теплогидродинамические процессы в устройствах охлаждения микросхем вычислительной техники. В статье [16] изучались магнитогидродинамические эффекты на нестационарное вращательное течение несжимаемой жидкости. Уравнения математической модели описывали нестационарное течение несжимаемой жидкости с частицами, движущимися под действием термофореза. С помощью пакета MATLAB уравнения математической модели интегрируются численным методом конечных элементов. В публикации [17] получена двухмерная численная модель детонации в неоднородной среде, основанная на методе Эйлера – Лагранжа и учитывающая дробление капель. Модель учитывала межфазный обмен массой, импульсом и межфазный теплообмен. Было обнаружено существенное влияние межфазного взаимодействия на процесс детонации. Без применения полного гидродинамического подхода, используя уравнения акустики, в исследовании [18] численно моделировалась конденсация атмосферного аэрозоля, образующегося в результате эксплуатации объектов промышленной энергетики, рассмотрены различные механизмы конденсации капель аэрозоля. В приведенных выше исследованиях объектом исследования являются различные виды течений в неоднородных средах. Это могут быть запыленные среды без фазовых переходов либо же дисперсные среды, в которых происходит дробление или же испарение дисперсной фазы, что обусловлено практическими приложениями, связанными с различными промышленными технологиями. Новизна работы заключается в том, что динамика полидисперсной парокапельной среды в осесимметричной постановке исследована с учетом межфазного обмена импульсом и теплом, а также азимутальной составляющей скорости обоих фаз смеси. Целью работы было исследование течения парокапельной среды с различными размерами дисперсных включений в трубе с нагретой стенкой. Выявлены отличия в распределении концентрации дисперсной компоненты с различными размерами капель при учете их испарения.

Постановка задачи

Парокапельная смесь состоит из дисперсной фазы, включающей в себя четыре капельных фракции жидкого метана и паров метана. Фракция мелкодисперсных включений состоит из капель с диаметром d = 2 мкм. Фракция крупнодисперсных капель образована каплями с диаметром d = 100 мкм. Также присутствуют капли с промежуточным размером d = 20 мкм и d = 40 мкм. Скорость звука в парах метана составляет c = (γ RT )^1/2 ≈ 297 м/с, где γ = 1,31 – постоянная адиабаты, R = 518 Дж/(кг∙К) – газовая постоянная метана. При величине радиальной координаты у = L y фиксировалась температура нагретой стенки. В численных расчетах количество узлов в осевом направлении – N_x , в радиальном направлении – N_y , расчетная сетка задавалась равномерной по всем пространственным направлениям с количеством узлов N x x N y = 200 x 100. На входной границе x = 0 задавалось однородное граничное условие Неймана для всех газодинамических функций. На оси симметрии при y = 0 и на стенках ( y = h ) для азимутальных составлющих скоростей компонент смеси задавались однородные граничные условия Дирехле. На твердой поверхности для всех составляющих векторов скоростей паровой фазы и дисперсных фракций задаются однородные граничные условия Дирихле. Для давления, плотности, энергии пара и температуры на выходе из трубы ставились однородные граничные условия Неймана. В численных расчетах задавались следующие значения скоростей паровой фазы и фракций жидкой компоненты смеси: u ( t = 0, x , y ) = 0,05 с 0 , v ( t = 0, x , y ) = 0, w ( t = 0, x , y ) = 0,1 с 0 , u i ( t = 0, x , y ) = 0,05 с 0 , v i ( t = 0, x , y ) = 0, w i ( t = 0, x , y ) = 0. Начальная температура фракций дисперсной фазы – T i = 108 К, начальное объемное содержание фракций – α i = 0,00025. Физическая плотность дисперсной фазы – ρ ж = 416 кг/м³, начальные температура и плотность пара – T 0 = 130 К, ρ 0 = 1,29 кг/м³. Температура стенки трубы составляла Т w = 200 К.

Теоретическая часть

Течение парокапельной среды моделировалось системой уравнений динамики многоскоростной и многотемпературной газовзвеси [19, 20] c вязкой несущей средой [21], включающей в себя несколько фракций. Моделируемое течение имеет осевую симметрию [20]:

др + д ( р u ) + д ( р v ) д t    д x     д у

Р v   .

--+ j ,

y

^д(р ^и )   д /    2            \   д /           \

⁺ — ( р ^{и +} Р ^— Т xx ) ⁺ — ( р uv ^{— Т} xy ) = д t     д x ^х                 '   д у ^х           ’

—

Р ^{uv Т} xy

y

д Р

^— Z F xi ^+a^ ⁺ j ' ^u , i = 1, n           ^д x

^д(р ^v )   д /           \   д /    2           \

—— ⁺ —(р uv ^{— т} xy ) ⁺ — ( р ^{v +} Р ^т уу ) = д t     д x ^х            '   д у '               '

—

Р v ⁺ Р ^{— т} уу

y

д Р

^— Z ^Fyi ^+a^ ⁺ j ■ v , i = 1, n           ^д у

д ( р w ) д ( р uw ) д ( р vw )     р vw

——— +—--— +—--— = — -

д t

д x

д у

y

— Z F i , i = 1, n

д e д (_г . д T — + — I e + p — т_гх I и — т.., v + Л— д t д x V xx^J xy д x

, д T v — т„ и + Л— x     д у

[ e ⁺ Р ^{— T} уу ] ^{v — T} xy^{u + Л}

------------ ----------^{у —} Z Q i ^— Z (I F xi l^{( u —} u i ⁾⁺I F ni^^{v —} v ) ) + ^у                       i = 1, n i = 1, n

( д ( pu ) д ( pv ) ) . _{r T} .2    2хЛ

+a I1I + j ■ L , e = I + p( u + v )/2, a= / ^ a

V ^{д x       д} у J                                        i = 1, n

(,д u  2 ^)         (, д v  2 ^]         (д u  д v ]  „ д u  д v  v

^T xx = P I ²~ ^— ” D I , ^T уу = P 2T"^— T D , ^T xy = P T ⁺ T , D =^Г⁺я , кд x  3 J        V д у  3 J        (д у  д x J д x  д у  у

Fa = 3 ТгЧ C di pV( ^{U — U}i ) 2 ⁺( ^{v —} vi ) ⁺( w ^— w i ) ² ( ^{U — U}i ) ⁺

⁴ ( ² ri)

( 8 u    d u   d u |        fd u    d u   d u  d u

+a i pl — + и — + v — I + 0,5 a i pl — + и —+ v---

(d t    d x    d y )         (d t     8 x    d y    8 1

—

8 U; ^ui ⁱ

8 x

—

8 и | v- I , 8 y )

F yi = 3 TTC C di p V( ^{U — U}i ) 2 ⁺( v ^— v ) 2 ⁺( w ^— w i ) 2 ( v ^— v ) ^{+ 4 ( 2} r i )

f 8 v    8 v    8 v |          (8 v    8 v    8 v  8 v_f

+a i pl — + и — + v — I + 0,5 a i pl — + и — + v

(8 t    8 x   8 y )        (8 t    8 x   8 y  8 t

—

8 v u_i ⁱ

8 x

—

8 v | v i - I, 8 y )

F zi = 3 T iT C C dip^ ( ^{U — U}i ' ) 2 ⁺( v ^— v ) 2 ⁺( w ^— w i ) ² ( w ^— w i ) , ⁴ ( ² ri )

C di = C di ^ ( M_toWiY C di =

f

1<Г ⁺ 1^0,5 ⁺ 0,4 (1 ^{+ 0} - ^{25 №} ’°¹/ Lp⁰* " ), ( ^Re i 0 ^Re i 0        )

v ( M io 0 ) = ¹ + exp

^{f 0,427} )

—

( M ^J

, ф ( а i ) = ( 1 ^{— a} i )

^2,5, Re i o =p V — Vd^ ,

Mi 0 = V ^— VJc , We i =p V ^— V if d i /с , ^L P i pⁿ d i A² , J = 2 Ji .

i = 1, n

В записи формул применяются обозначения: u, v, w, ui, vi, wi – пространственные компоненты векторов скорости несущей среды и фракций дисперсной фазы; р, е, с, X, ц, di - плотность несущей среды, удельная полная энергия, коэффициент поверхностного натяжения несущей фазы, коэффициент теплопроводности и коэффициент вязкости несущей фазы, диаметр капли i-й фракции; ji – интенсивность массообмена между i-й фракцией дисперсной фазы и несущей средой. Объемное содержание жидкой фазы парокапельной среды является суммой объемных содержаний фракций: a = 2 ai. Коэффициент аэродинамического сопро-i=1,n тивления капель Сdi описывается с учетом сжимаемости несущей фазы ψ(Мi0) и большого объемного содержания дисперсных включений φ(αi) [2]. При описании динамики несущей фазы смеси учитывалось уравнение для азимутальной составляющей импульса, записанное в предположении об азимутальной симметрии потока при его вращении и без учета составляющих вязкого трения [22]. Пространственные компоненты вектора обмена импульсом между несущей фазой и i-й фракцией – Fxi, Fyi, Fzi [1–3, 22]. Здесь I = ρRT/(γ – 1) – внутренняя энергия газа; R, γ – газовая постоянная и постоянная адиабаты несущей

1) (e /ρ – 0,5( u ² + v ²))/ R ;

среды соответственно. Температура несущей среды определяется как T = (γ

-

Q i = 6α i Nu i λ ( T - T i )/(2 r i )² – тепловой поток [1, 2, 13], возникающий вследствие теплообмена между несущей средой и каплями i -й фракции, где Nu i = 2 r i α p /λ – число Нуссельта, r i – радиус капель i -й фракции. Число Нуссельта определяется при помощи известного из литературы приближения [1, 2]. Дисперсная фаза парокапельной смеси имеет многофракционный состав – фракции отличаются размером капель. Для каждой фракции дисперсной фазы решается полная гидродинамическая система уравнений с учетом обмена массой, импульсом и тепловой энергией между фракциями дисперсной фазы и несущей средой [20]:

⁸ p i + ^{8 (} p iud + ^{d (} P i^vi )

8 t     8 x

8 y

—

p i v i ^y

—

j i ,

^d ( p i ^Ui ) ₊_d_ d t      d x

( ^p i^u 2 ) + d y ( ^p i u i- v / ) =

—

ft Uvi  v

1 1 1 1 A. P .

xi

—

d ( p_z vi ) d ,        , d /

—---- + — ( p/ uvi ) + — p v / = — d t        8x^v i i’ 8y' i /

y p^Lf-yi y

dp ai--Ji • ui, dx

—

8p a i -— Ji • vi, 8y

d ( p iWi ) д ₍         \ 8 (        \     p v,-w,

---⁺ — ( p i uiwi ) ⁺ — ( p ^vi w i ) =-- ⁺ F zi ,

8 1     8 x            8 y^x      ' y

8""L + "8"(eUi) + "8-(ev) = — ei-i- + Nuz 6ai2 X(T — T) — Ji ■ L, 81    8x^ 1 i7 8yV i i’ y 1 (2r)2 V i7 vi , pi =aipio, ei = piCpiTi, j =2 j.

i = 1, n

Давление паровой фазы смеси определяется следующим уравнением p = p rt[ ^f 1 - р ж ) , / к Р ж )

где Т, R, ρ – температура пара, газовая постоянная и плотность пара; ρж – суммарная средняя плотность капель по всем фракциям. Здесь ρ0ж – истинная плотность дисперсной фазы; ρж ρ0ж – объемная доля смеси, занимаемая дисперсной фазой. Испарение мелкодисперсных капель описывается математической моделью [8, 20]. Математическая модель предполагала, что при поглощении теплоты парообразования про- исходит уменьшение температуры пара.

Для крупных дисперсных включений жидкой фазы использовалась математическая модель изменения температуры и массы капель [7, 20]. Температура движущейся в потоке крупнодисперсной капли описывается дифференциальным уравнением

д Tp д t

^{6 а} pi d i C p ж ^р ж

^{f 1} + ^МОтн

^-1) Vf l + m² ( ^Y- ¹⁾ 1- T 2 )! к         2 )

где М отн – относительное число Маха, М отн = | V - V i |/ с ; С р ж , ρ ж – удельные теплоемкость и плотность жидкости; T – температура несущей среды. Здесь α pi = Nu∙λ/ d i – коэффициент поверхностного теплообмена между несущей средой и поверхностью капли i -й фракции. Процесс испарения капли описывается дифференциальным уравнением

д mi

д t

ⁿ di ^2a pi L ( T p )

T f l + m O _th

^{( Y} - ¹⁾ 1/f i + m²^ 1- T ( p )

2 )/ к          2 )

В формуле (5) при температуре Т_р L ( T_p ) – теплота парообразования жидкости; для давления р Т_s ( p ) – температура насыщения; m_i – масса капли i -й фракции. Решение дифференциальных уравнений (4), (5) осуществляется численным методом Эйлера [23]:

д TD (t)

T p ( t + A t ) » T p ( t ) +       A t ,

д t дm, (t) A m, (t + At) ® m (t) +------- A t,

ix,      дt

Система уравнений математической модели динамики двухфазной полидисперсной парокапельной смеси интегрировалась явным конечно-разностным методом Мак-Кормака [24] c оператором расщепления по пространственным направлениям [25]. Для подавления численных осцилляций применялась схема нелинейной коррекции сеточной функции [26]. Термодинамические параметры жидкой и паровой компонент парокапельной метановой смеси определялись известными из литературы аппроксимациями [27, 28].

Практическая часть

В конструкцию устройства технологического нагревателя газожидкостных смесей входят коаксиально расположенные цилиндрические трубы с нагреваемыми боковыми стенками (рис. 1) [4].

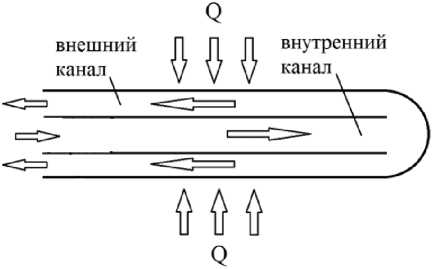
Рис. 1. Схематичное изображение коаксиальных труб в устройстве нагревателя газожидкостных смесей Fig. 1. A schematic representation of coaxial pipes in a heater for gas-liquid mixtures

На рис. 2а схематически изображена расчетная обаласть – цилиндрическая труба. Длина моделируемой трубы составляет L_x = 1 м, радиус трубы – L_y = 0,1 м; неоднородная среда втекает в трубу при x = 0 и вытекает из трубы при x = 1 м (рис. 2b).

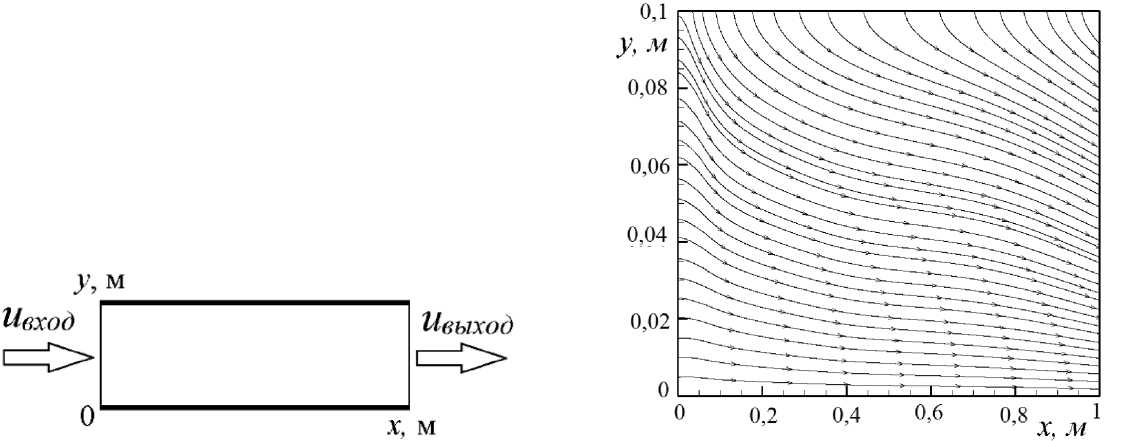
Рис. 2. Схематичное изображение моделируемой области (а), векторное поле скоростей паровой фазы, момент времени t =1,5 с (b)

Fig. 2. A schematic representation of the simulated area (a), vector field of vapor phase velocities, time t = 1.5 s (b)

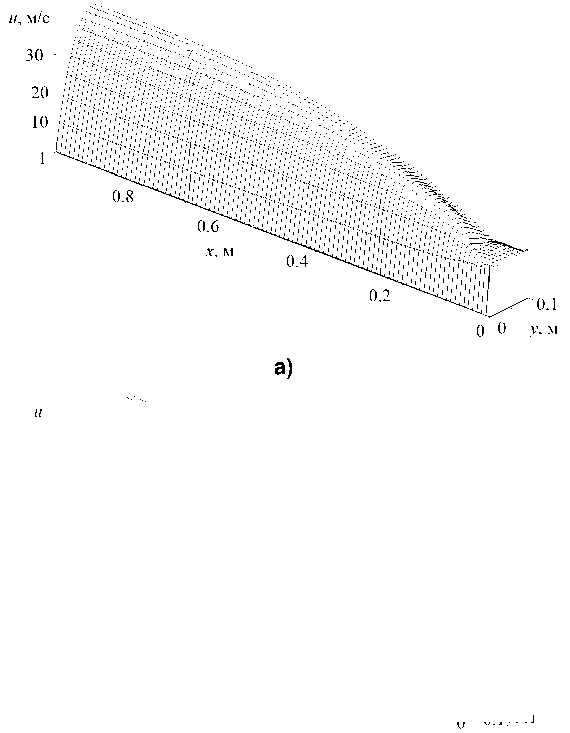
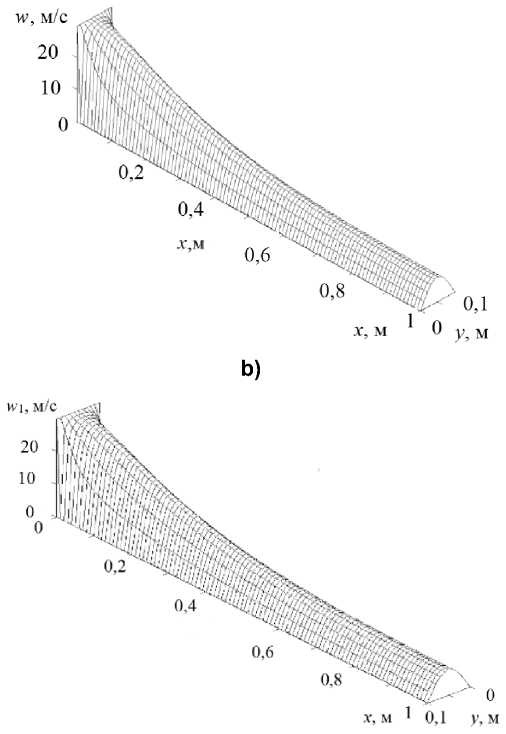
На рис. 3a–d представлены результаты расчетов азимутальной и продольной составляющих скорости для несущей фазы и фракции мелкодисперсных капель c диаметром d = 2 мкм. Составляющие скоростей мелкодисперсных капель и несущей среды согласуются между собой. При задании равномерного граничного условия на входе в трубу для продольной составляющей вектора ско- рости наблюдается формирование из изначально равномерного распределения скорости «параболического» профиля, характерного для течения вязкой среды [21]. Азимутальная составляющая скорости значительно убывает по сравнению со значением, заданным на входном отверстии, при прохождении трубы, что согласуется с теоретическими выкладками [22]. В поперечном направлении

c)

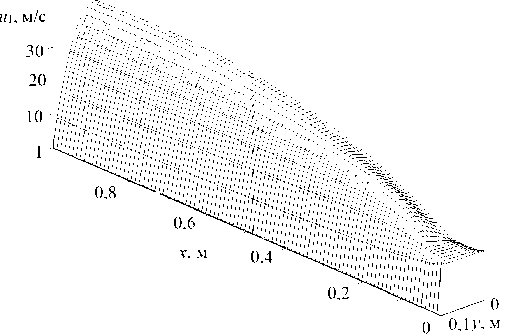
Рис. 3. Пространственное распределение продольной и азимутальной составляющих скорости несущей среды (a, b) и фракции дисперсной компоненты с размером капель d = 2 мкм (c, d)

Fig. 3. The spatial distribution of the longitudinal and azimuthal components of the velocity of the carrier medium (a, b) and the fraction of the dispersed component with a droplet size d = 2 μm (c, d)

d)

наибольшее значение азимутальной и продольной составляющих векторов скорости достигается между осью симметрии трубы и поверхностью стенки (рис. 3b, d).

На рис. 4а–с представлены пространственные распределения температуры несущей фазы и температуры двух фракций дисперсной фазы с различными размерами капель. Для мелкодисперсных капель ( d = 2 мкм) отличие поля температуры от поля температуры несуйщей фазы несущественно, тогда как для фракции капель с диаметром d = 20 мкм распределение температуры лишь на несколько градусов отличается от их начальной температуры. Распределение температуры мелкодисперсных капель ( d = 2 мкм) имеет наибольшее значение вблизи стенки, распределение температуры фракции мелкодисперсных капель ( d = 20 мкм) равномерное.

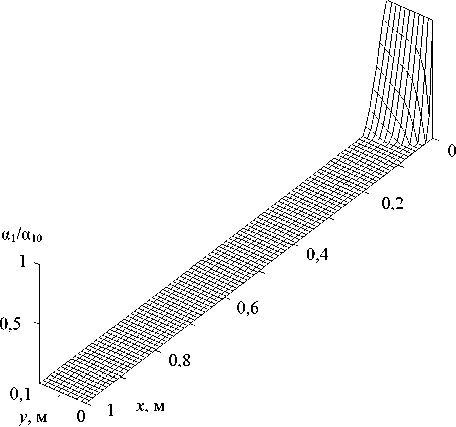
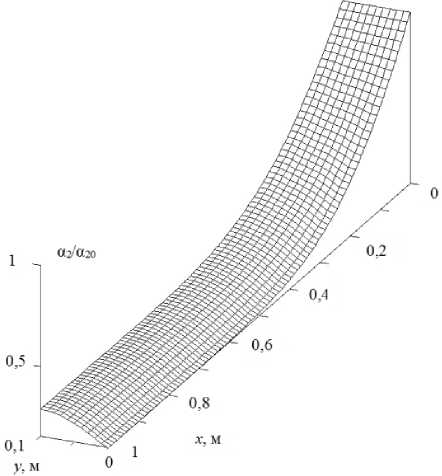
На рис. 5a–d для каждой фракции дисперсной фазы представлены двухмерные распределения отношения объемного содержания фракции на входе в трубу и на всём протяжении трубы. Мелкодисперсные фракции испаряются непосредственно вблизи входа в трубу (рис. 5а). Чем больше размер капель, составляющих фракцию дисперсной фазы, тем меньший объем данной фракции испаряется при прохождении трубы с заданной длинной. Для крупнодисперсных капель диамет- ром d = 100 мкм при прохождении трубы капли не успевают испариться. За счет скоростного скольжения и пристеночной вязкости капли замедляют движение и объемное содержание фракции крупнодисперсных капель выше, чем при входе в трубу.

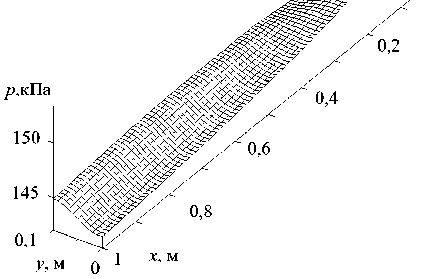
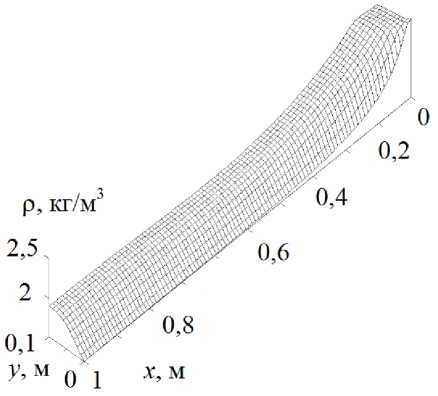
На рис. 6 представлены двухмерные распределения давления (рис. 6а) и плотности (рис. 6b) паровой фазы смеси. За счет испарения мелкодисперсных капель происходит увеличение плотности паровой фазы, наибольшее значение давления и плотности несущей фазы наблюдается вблизи входного отверстия трубы.

В результате моделирования определено, что закономерности испарения капель различного размера в трубе-нагревателе отличаются. Численные расчеты демонстрируют, что крупнодисперсные капли не только не испаряются. Для мелкодисперсной фракции капель ( d = 2 мкм) наблюдается хорошее согласование полей скорости и температуры с несущей фазой. Объемное содержание крупнодисперсной фракции капель в трубе немного выше начального объемного содержания крупнодисперсных капель на входе в трубу. Также численные расчеты показывают, что за счет испарения мелкодисперсных фракций наблюдается возрастание давления паровой фазы смеси вблизи входного отверстия в канал.

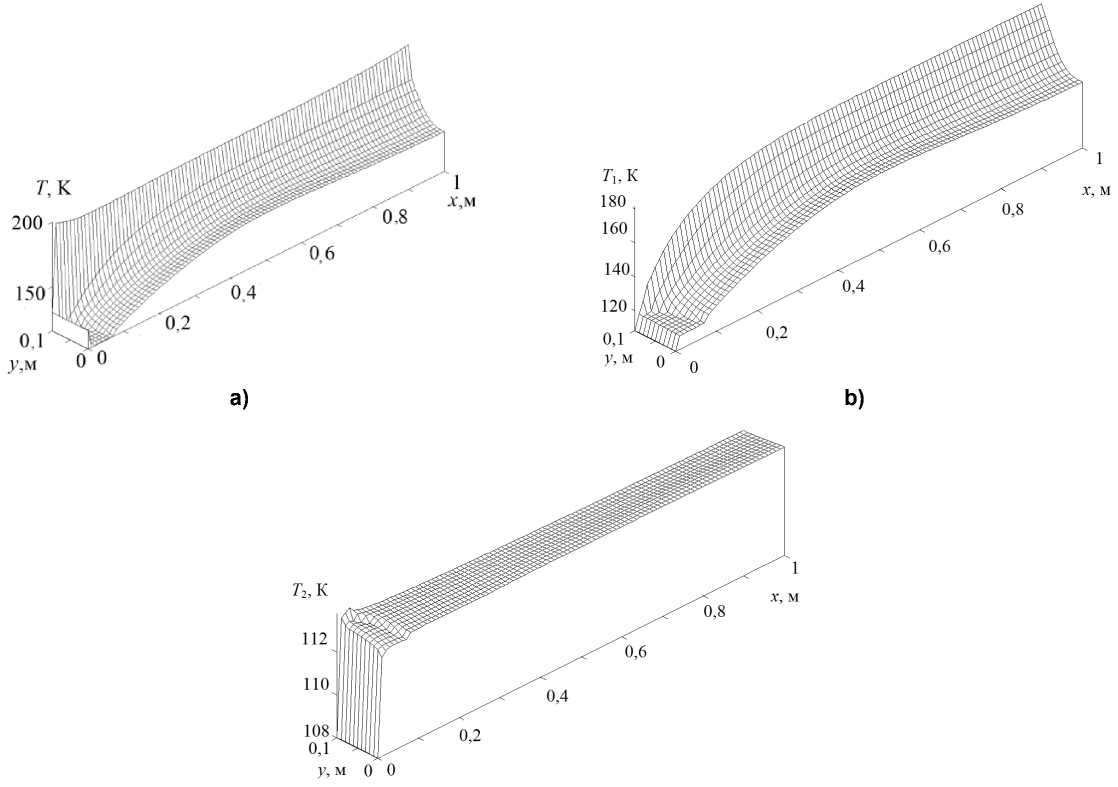
c)

Рис. 4. Пространственное распределение температуры компонент смеси: а – несущая среда; b – фракция с начальным размером 1 мкм; c – фракция с начальным размером d = 20 мкм Fig. 4. The spatial temperature distribution of the mixture components: a – carrier medium; b – fraction with an initial size of 1 μm; c – fraction with initial size d = 20 µm

а)

b)

c)

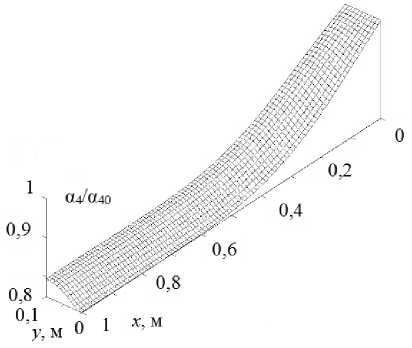
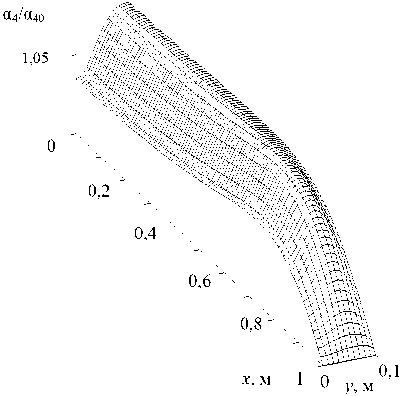
Рис. 5. Пространственное распределение средних плотностей дисперсных фракций: a – фракция с начальным размером 2 мкм; b – фракция с начальным размером 20 мкм; c – фракция с начальным размером 40 мкм; d – фракция с начальным размером 100 мкм

Fig. 5. The spatial distribution of the average densities of the dispersed fractions: a – fraction with an initial size of 2 μm; b – fraction with an initial size of 20 μm; c – fraction with an initial size of 40 µm; d – fraction with an initial size of 100 μm

d)

а)

b)

Рис. 6. Пространственное распределение давления (а), плотности (b) несущей среды Fig. 6. The spatial distribution of pressure (a), density (b) of the carrier medium

Заключение

В работе проведены численные расчеты динамики пара с многофракционной дисперсной фазой с учетом теплообмена и обмена импульсом между несущей средой и дисперсной компонентой. Математическая модель учитывала азимутальную составляющею скорости капель и их испарение. Численное моделирование демонстрирует, что азимутальная составляющая течения несущей среды существенно уменьшается вдоль трубы. Поперек трубы, между осью симметрии трубы и стенкой, происходит возрастание азимутальной составляющей скорости несущей среды. Скоростная и температурная дифференциация между несущей фазой и фракцией мелкодисперсных капель не имеет существенного значения. По причине малого отличия поля температуры несущей фазы и фракции мелкодисперсных капель мелкодисперсные капли размером d = 2 мкм почти полностью испаряются на входе в трубу. Также в процессе движения по трубе происходит существенное уменьшение фракций дисперсной фазы с размером капель d = 20 мкм и d = 40 мкм. Крупнодисперсные капли d = 100 мкм из-за своей массы при движении по трубе не успевают испариться и из-за скоростного скольжения накапливаются в трубе, и их объемное содержание несколько выше объемного содержание на входе в трубу. Из-за испарения мелкодисперных капель в трубе, особенно вблизи входного отверстия, наблюдается увеличение плотности и давления паровой фазы. Выявленные закономерности течения испаряющейся парокапельной смеси с полидисперсным составом жидкостной фазой в цилиндрической трубе с нагретыми стенками могут быть использованы при оптимизации работы теплообменных труб, применяемых в устройстве нагревателя газожидкостных смесей [4].