Численное моделирование динамики температуры и диэлектрических параметров нефтематеринской породы при СВЧ-нагреве

Актуальность и практическая значимость данной работы связана с необходимостью решения проблемы, остро вставшей перед российской нефтяной отраслью и связанной с существенным увеличением доли трудноизвлекаемых запасов в общей структуре запасов нефти. Месторождения трудноизвлекаемых запасов характеризуются сложным геологическим строением, низкой проницаемостью коллекторов и высокой вязкостью нефти. И если в мире добыча трудноизвлекаемых запасов составляет примерно 20 % от общей добычи, то в России вовлечено в разработку менее 1 %. Отчасти это объясняется тем, что эффективная разработка таких месторождений не может быть обеспечена существующими технологиями. Необходима разработка новых технологий, основанных на воздействии на пласт физическими полями. Одним из таких воздействий является электромагнитное воздействие на нефтеносную породу, направленное на её нагрев по меньшей мере в призабойной зоне пласта.

Физика процесса электромагнитного нагрева основана на характере поведения диэлектриков в электрических полях. Полярные молекулы диэлектрика ориентируются вдоль силовых линий внешнего электрического поля, так что направление их дипольного момента совпадает с направлением внешнего поля. В переменном электрическом поле молекулы начинают совершать вращательные движения, при этом часть энергии электрического поля уходит на работу поворота молекул. Количество энергии, ушедшей на поляризацию дипольных молекул, оценивается величиной тангенса угла диэлектрических потерь, который является отношением активной составляющей электрического тока к реактивной. В идеальном диэлектрике величина тангенса угла диэлектрических потерь равна нулю.

Было показано, что плотность распределения тепловых источников в объеме диэлектрика при его электромагнитном нагреве выражается через диэлектрическую проницаемость и тангенс угла диэлектрических потерь [1].

По сравнению с традиционными методами нагрева призабойной зоны электромагнитный нагрев имеет ряд преимуществ: более высокая скорость нагрева, отсутствие необходимости прямого контакта между источником нагрева и нагреваемым материалом, возможность избирательного нагрева, увеличение степени контроля процесса нагрева, уменьшение размера оборудования и количества отходов.

Текущее состояние исследований и разработок указывает на то, что электромагнитная энергия может сыграть важную и, возможно, решающую роль в технологиях извлечения углеводородов из нефтематеринских пород [2–4].

В случае коллекторов и сланцев, содержащих кероген, при воздействии на них электромагнитных полей (ЭМП) нагрев происходит в достаточно широком диапазоне частот: от 100 кГц до 2,4 ГГц. Нагрев нефтяных сланцев до температур в диапазоне 200–360 °C и выдерживание их при данных температурах в течение определенного периода времени приводит к процессу пиролиза, в ходе которого из сланца выделяются маловязкая нефть, газ и пар [5–6].

Если электромагнитное поле действует на сланец путем всенаправленной антенны и тщательно контролируется по амплитуде и согласованию, оно будет постепенно проникать в сланцевый пласт, обеспечивая высокое извлечение нефти. Кроме этого, воздействие электромагнитного поля определенной частоты на сланцевую породу может привести к развитию в ней термоупругих напряжений, трещиноватости, разупрочнению и разрушению породы [7]. Термические напряжения возникают в результате термического расширения породы при её неравномерном нагреве, вызванном неоднородным распределением диэлектрических параметров [8–9].

Ключевой задачей при этом подходе является подбор оптимальных для среды с данными диэлектрическими параметрами частоты и мощности излучателя электромагнитного поля, поскольку от них зависят как скорость нагрева, так и геометрия области нагрева. Затрудняется это тем, что диэлектрические параметры среды зависят не только от её состава, но и от частоты приложенного ЭМП и от температуры [10–12]. Как правило, диэлектрические параметры измеряются соответствующим оборудованием. Этот подход ограничен тем, что это оборудование является относительно труднодоступным и дорогостоящим, а также ограниченным по частотному диапазону. Более того, с ростом температуры значительно увеличивается погрешность измерения диэлектрических параметров. В связи с этим в данной работе предложен метод определения их температурной зависимости по экспериментальным данным электромагнитного нагрева. Валидность метода подтверждена количественным совпадением экспериментальных данных с результатами численного моделирования. Проведено сравнение моделей электромагнитного нагрева с постоянными и однородными диэлектрическими свойствами, зависящими от температуры.

Экспериментальное исследование

В качестве объекта исследования был выбран образец горной породы баженовской свиты цилиндрической формы длиной 12 см и диаметром 10 см. На рис. 1 приведена схема лабораторного стенда. Слева установлен волновод с магнетроном ( ω = 2,45 ГГц, P = 800 Вт). Справа под защитным экраном расположен образец керна, который был теплоизолирован. Замер температуры проводился при помощи системы термопар, помещённых на поверхность образца, и регистратора температуры. Термопары пронумерованы по направлению от излучателя и расположены на расстоянии 1 см друг от друга.

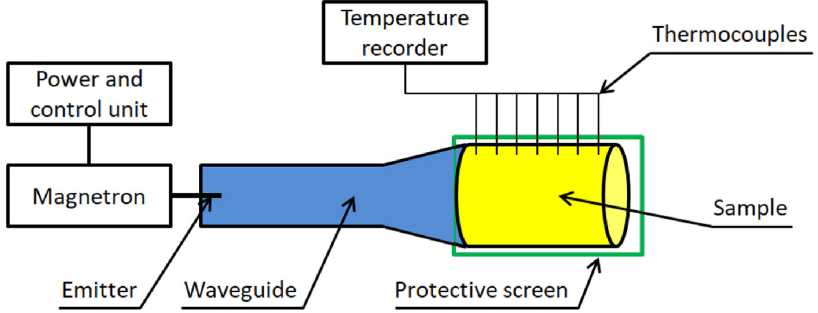
Рис. 1. Схема лабораторной установки для исследования распределения температуры в образце нефтематеринской породы при воздействии микроволновым излучением

Fig. 1. Schematic layout of the laboratory setup for studying the temperature distribution in a source rock sample under microwave irradiation

Постановка задачи

Рассматривается образец нефтематеринской породы цилиндрической формы длиной L и диаметром D . Ввиду радиальной симметрии моделируемой установки расчётная область является двумерной. Её схема приведена на рис. 2. В расчётную область входит только сам образец, как видно по расположению координатной оси. Считается, что он помещается в область воздействия СВЧ электромагнитного поля, под действием которого в среде возникают внутренние распределенные источники тепла.

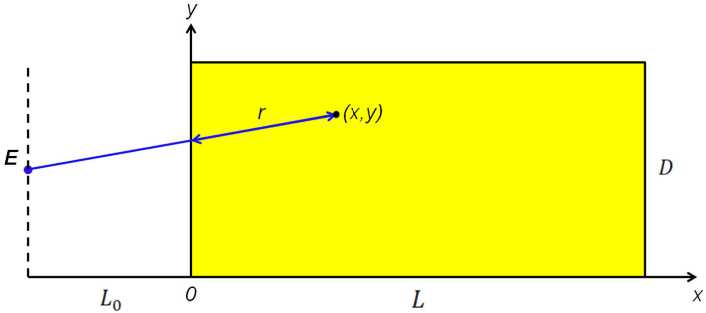
Рис. 2. Схема расчетной области

Fig. 2. Scheme of the computational domain

При построении математической модели насыщенная пористая среда рассматривается как сплошная среда с осредненными значениями физических величин. Рассматривается однотемпературная постановка задачи. Источник ЭМП считается точечным и расположенным от образца на расстоянии L 0 , как показано на рис. 2. В первоначальной постановке считается, что физические параметры насыщенной пористой среды, включая диэлектрические, не изменяются в процессе электромагнитного воздействия.

Математическая модель

Распределение температуры определяется из решения уравнения теплопроводности для насыщенной пористой среды с распределенными источниками тепла [13]:

ат at

Л q

= — дт + —

ср ср

где cρ – объемная теплоемкость; λ – коэффициент теплопроводности; q – плотность распределенных источников тепла.

Считается, что в начальный момент времени распределение температуры однородно, а все грани образца теплоизолированы:

Т(х,у, t = 0) = Т_о V Т\_г — 0,

где Г – граница расчетной области.

В соответствии с условиями проведения эксперимента плотность распределенных источников тепла записывается с учетом затухания электромагнитной волны:

q = 2аР₀е^-2“^г                                                       (3)

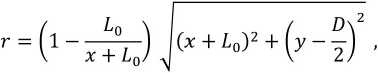
где α – коэффициент поглощения электромагнитной волны; P₀ – плотность потока энергии, излучаемой магнетроном; L 0 – расстояние от источника ЭМП до образца, D – диаметр образца, x и y – координаты расчётной точки, r – длина проникновения электромагнитной волны в образец, отсчитываемая от точки вхождения до расчётной точки, как показано на рис. 2.

Коэффициент поглощения α является интегральным параметром, отображающим диэлектрические свойства материала в электромагнитном поле данной частоты:

anTctgS а =                                                                     (5)

где ω – циклическая частота электромагнитного поля, ε – диэлектрическая проницаемость, tgδ – тангенс угла диэлектрических потерь, с – скорость света. Его физический смысл заключается в степени поглощения энергии электромагнитной волны при её распространении через среду.

Плотность потока энергии P₀ определяется как отношение выходной мощности магнетрона P к площади сечения образца:

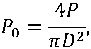
Табл. 1. Расчетные параметры

Table 1. Modeling parameters

Длина расчетной области L	12	см
Диаметр расчетной области D	10	см
Расстояние от источника ЭМП до образца L 0	10	см
Начальная температура T0	20	°C
Выходная мощность магнетрона P	800	Вт
Плотность образца породы ρ	2700	кг/м3
Теплоемкость образца породы c	1050	Дж/(кг·К)
Коэффициент теплопроводности образца породы λ	1.9	Вт/(м·K)

Математическая модель была реализована в открытой программной среде FreeFem, ориентированной на решение дифференциальных уравнений в частных производных с использованием метода конечных элементов. Были использованы следующие расчётные параметры.

В первоначальной постановке коэффициент поглощения электромагнитной волны α был определён валидацией модели экспериментальными данными и составил 5.8 м^-1. Сопоставление результатов моделирования с экспериментальными данными приведено на рис. 3–4. Зависимость температуры от времени варьируется по координате x , а от координаты x – по времени. Маркерами обозначены экспериментальные данные, а линиями соответствующего цвета – результаты моделирования. Цвет маркеров и линий соответствует определённому значению варьируемого параметра.

На рис. 3–4 видно, что расхождение между экспериментальными и численными кривыми тем больше, чем больше значение температуры. Количественное расхождение результатов

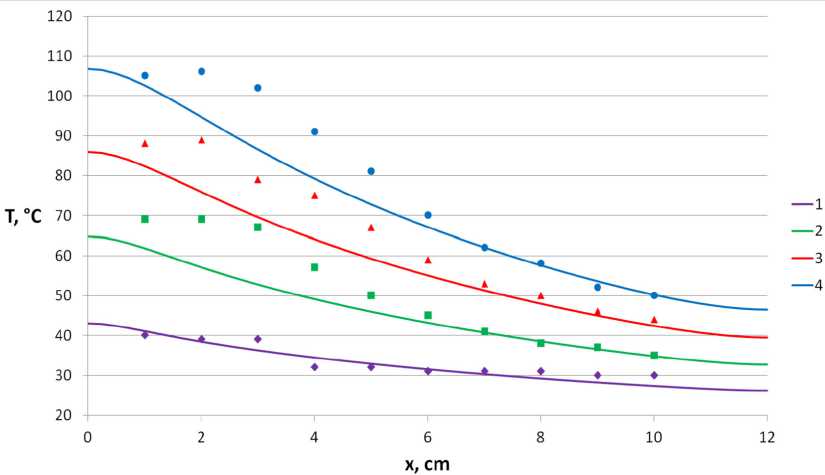
Рис. 3. Распределение температуры по длине образца в разные моменты времени; маркеры – эксперимент, линии – моделирование: 1–60 с, 2–120 с, 3–180 с, 4–240 с; α = 5.8 м^-1

Fig. 3. Temperature distribution along the length of the sample at different points in time: markers – experiment, lines – modeling; 1–60 s, 2–120 s, 3–180 s, 4–240 s; α = 5.8 m^-1

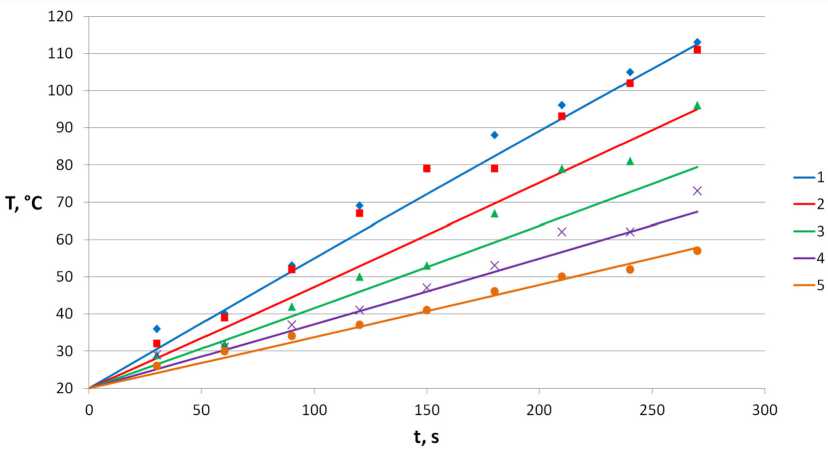
Рис. 4. Динамика температуры на разных участках образца; маркеры – эксперимент, линии – расчёт: 1–1 см, 2–3 см, 3–5 см, 4–7 см, 5–9 см; α = 5.8 м^-1

Fig. 4. Temperature dynamics in different parts of the sample; markers – experiment, lines – modeling: 1–1 cm, 2–3 cm, 3–5 cm, 4–7 cm, 5–9 cm; α = 5.8 m^-1

может быть обусловлено тем, что диэлектрическая проницаемость и тангенс угла диэлектрических потерь изменяются в зависимости от температуры. При этом характер этих изменений уникален для всех материалов, их структуры, насыщенности и т.д. Существуют лишь зависимости этих параметров от температуры в определенном диапазоне частот, которые устанавливаются экспериментально для каждого отдельного материала и диапазона частот. В данной постановке коэффициент поглощения α считается постоянным, что и вызывает значительное расхождение с экспериментом.

Также на основе этой модели было спрогнозировано время достижения образцом температуры 300 °C и глубина проникновения области с температурой выше 300 °C в конечный момент времени. В некоторых породах при этих температурах происходит пиролиз [14]. Расчетная область остается такой же, за исключением увеличения ее длины до 50 см. На рис. 5 представлено распределение температуры по длине образца в разные моменты времени.

Из рис. 5 видно, что тепловой фронт за 1200 с достигает глубины примерно в 35 см, хотя самые высокие температуры наблюдаются лишь до 5–10 см. Область, в которой возможен пиролиз, на этот момент времени составляет около 5 см. Температура 300 °C достигается примерно за 800 с. Это время может быть обозначено как время начала пиролиза в образце.

Решение обратной задачи

Для увеличения достоверности модели был разработан метод косвенного определения температурной зависимости коэффициента поглощения α путём решения обратной задачи, суть которого заключается в выражении коэффициента поглощения α через остальные известные параметры модели.

Формула распределённых источников тепла умножается и делится на r , и производится замена γ = 2αr :

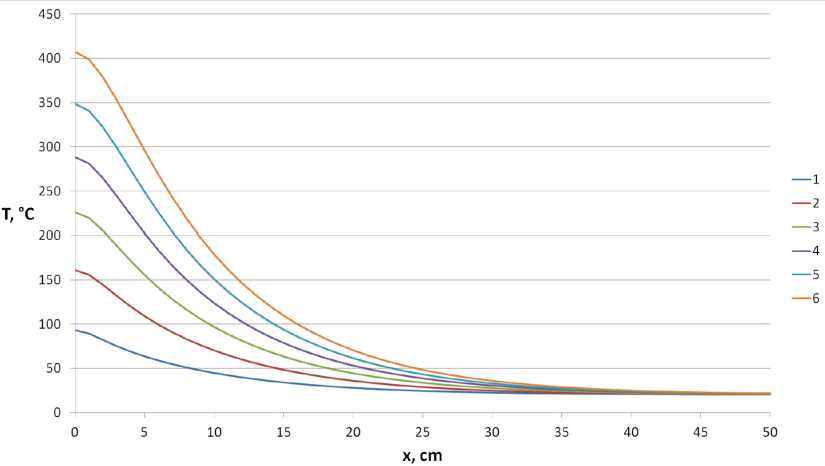
Рис. 5. Прогнозируемое распределение температуры по длине образца в разные моменты времени: 1–200 с, 2–400 с, 3–600 с, 4–800 с, 5–1000 с, 6–1200 с; α = 5.8 м^-1

Fig. 5. Predicted temperature distribution along the length of the sample at different points in time: 1–200 s, 2–400 s, 3–600 s, 4–800 s, 5–1000 s, 6–1200 s; α = 5.8 m^-1

9 D -2«r ^P^^{e У}

q = 2aPoe =------.

Затем из уравнения теплопроводности выражается q. Слагаемое λΔT много меньше cρ∙∂T/∂t , поэтому им можно пренебречь:

dT A q         дТ          dT

— = — AT H-- =^ q = cp —--АЛТ ^ cp —. dt cp cp ^H dt          ^p dt

Производная температуры по времени дискретизируется и рассчитывается по экспери- ментальным данным:

дТ Т,₊₁-Т,

Два выражения q приравниваются, и из этого уравнения выражается ye Y :

ЭТ

7^' = -^-

Обозначим правую часть этого уравнения как Φ . Получим следующее уравнение:

ye-Y — ф ^> у — -W(-O), где W обозначает функцию Ламберта. Наконец, рассчитываются значения коэффициента поглощения α:

Полученные значения α сопоставляются соответствующим средним арифметическим температур, по которым они были рассчитаны. В итоге получается набор точек, который в первом приближении был аппроксимирован экспоненциальной зависимостью:

Данные температурной динамики были взяты с самых близлежащих к источнику ЭМП термопар ввиду того, что используемая формула распределённых источников тепла получена с предположением о постоянности и однородности коэффициента поглощения электромагнитной волны а [15]. Даже если предполагать однородность состава образца, это неверно ввиду неоднородности температурной зависимости, а от которой мы пытаемся установить. Соответственно, чем дальше от поверхности вхождения ЭМ волны в образец расположена термопара, тем менее валидно применение метода решения обратной задачи для определения её температурной зависимости. В данном случае использование данных с первых двух термопар допустимо, поскольку разница измеренных ими температур остаётся пренебрежимо малой на протяжении всего времени эксперимента.

Математическая модель, в свою очередь, также изменяется для учёта неоднородности коэффициента поглощения:

дР

На рис. 6–7 приведено сопоставление результатов реализации обновлённой модели с экспериментальными данными. Зависимость температуры от времени варьируется по координате x , а от координаты x – по времени. Маркерами обозначены экспериментальные данные, а линиями соответствующего цвета – результаты моделирования. Цвет маркеров и линий соответствует определённому значению варьируемого параметра.

На рис. 6–7 видно, что учёт температурной зависимости увеличил степень совпадения результатов моделирования с экспериментальными данными.

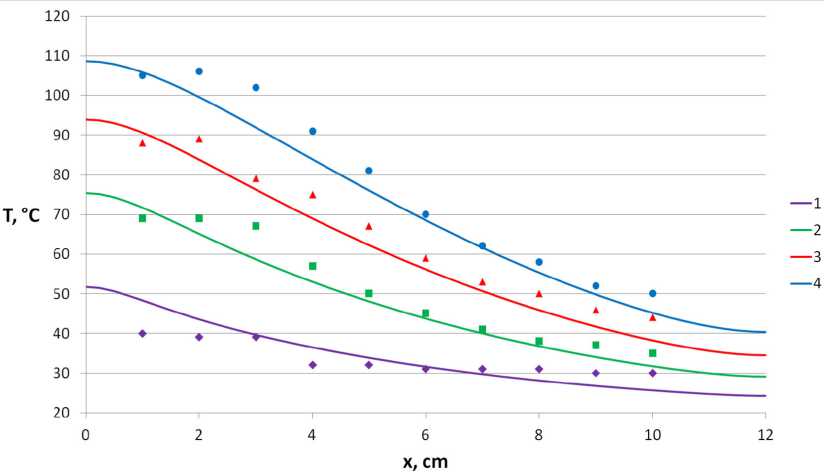
Рис. 6. Распределение температуры по длине образца в разные моменты времени: маркеры – эксперимент, линии - моделирование; 1-60 с, 2-120 с, 3-180 с, 4-240 с; а = а(Т)

Fig. 6. Temperature distribution along the length of the sample at different points in time: markers – experiment, lines - modeling; 1-60 s, 2-120 s, 3-180 s, 4-240 s; а = a(T)

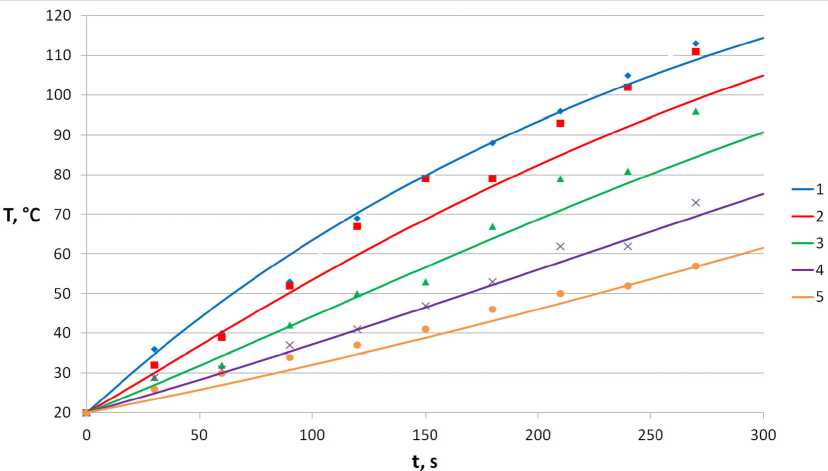
Рис. 7. Динамика температуры на разных участках образца: маркеры – эксперимент, линии – расчёт; 1–1 см, 2–3 см, 3–5 см, 4–7 см, 5–9 см; α = α(T)

Fig. 7. Temperature dynamics in different parts of the sample: markers – experiment, lines – modeling; 1–1 cm, 2–3 cm, 3–5 cm, 4–7 cm, 5–9 cm; α = α(T)

Заключение

В результате проведённого исследования показано, что предложенный метод позволяет приемлемо оценить температурную зависимость коэффициента поглощения α, отображающего диэлектрические параметры среды, находящейся под действием электромагнитного воздействия данной частоты. Ограничением этого метода является отсутствие возможности экстраполяции полученных зависимостей за пределы температурного диапазона, достигнутого в эксперименте. В соответствии с этим для его успешного применения в прогнозировании интенсивности и геометрии электромагнитного нагрева той или иной среды необходимы эксперименты, достигающие более высоких температур.