Численное моделирование движения ионов в газонаполненных магнитных масс-сепараторах

Газонаполненные масс-сепараторы обладают высоким аксептансом по заряду и скорости разделяемых ионов. Они широко используются в тех областях ядерной физики, где требуется высокое пропускание пучков заряженных частиц с широким зарядовым распределением и где их основной недостаток — невысокая разрешающая способность по массам — не играет большой роли [1]. Одна из таких областей — исследование продуктов полного слияния ядер в асимметричных реакциях с образованием сверхтяжелых элементов при бомбардировке быстрыми ионами твердых мишеней [2]. Чрезвычайная редкость процессов синтеза (сечение в 1011 раз меньше суммарного сечения всех остальных реакций) делает актуальным усовершенствование ионно-оптических схем газонаполненных сепараторов, направленное на увеличение их чувствительности и повышение эффективности очистки от продуктов побочных реакций.

В литературе представлено несколько работ, посвященных построению компьютерных моделей газонаполненных сепараторов [3–8]. Все эти модели основаны на методе статистического моделирования и привязаны к конкретным схемам сепараторов: GARIS в Осаке [3], HECK в Дармштадте [5], RITU в Jyväskylä [8], DGFRS в Дубне [6], BGS в Беркли [7]. Диспергирующим элементом сепаратора является дипольный магнит. С целью увеличения пропускания этот магнит либо имеет наклонные границы поля, обеспечивающие вертикальную фокусировку (GARIS, HECK, DGFRS), либо перед магнитом установлена вертикально фокусирующая квадрупольная линза (RITU, BGS). В работе [4] моделировался сепаратор на основе магнитного спектрографа, состоящего из двух магнитных диполей с общей обмоткой, разделенных областью слабого магнитного поля.

В указанных работах с той или иной степенью подробности учитывались основные физические процессы, происходящие при движении тяжелой заряженной частицы в газовой среде ионнооптического тракта сепаратора и влияющие на его характеристики. Такими процессами являются: 1) торможение ионов и уширение их энергетических распределений; 2) рассеяние на малые углы при столкновениях с молекулами газа; 3) флуктуации ионного заряда вследствие захвата и потери электронов при столкновениях.

Как отмечалось в работе [9], можно выделить четыре независимые составляющие вклада в полные размеры изображения в фокальной плоскости сепаратора:

• •    ионно-оптические аберрации и поперечные размеры пучка на выходе из мишени;

• •    скоростная зависимость среднего равновесного заряда иона;

• •    флуктуации ионного заряда;

• •    рассеяние ионов в газе.

Разрешающая способность сепаратора определяется главным образом последними тремя из указанных факторов. Уширение изображения пучка ионов в плоскости детектора за счет эффектов ионно-молекулярных столкновений существенно доминирует над вкладом в это уширение нелинейных эффектов движения ионов в магнитных полях.

Несмотря на большой объем моделирования, проведенного при разработке существующих схем газонаполненных сепараторов, в имеющейся литературе недостаточно полно приведено описание используемых при этом математических моделей. Настоящая работа призвана дополнить существующие описания для того, чтобы сделать возможным адекватный синтез и анализ различных схем газонаполненных сепараторов.

Отметим, что такой анализ требует развития существующего математического обеспечения расчетов газонаполненных сепараторов в двух аспектах. Во-первых, оптимизация новых ионнооптических схем требует разработки методов моделирования сепараторов, построенных на основе комбинации достаточно широкого набора дипольных и квадрупольных элементов, порядок следования которых может варьироваться. Метод компьютерного конфигурирования таких схем был разработан в работе [10]. Во-вторых, требуют уточнения и модели физических процессов, происходящих при транспортировке быстрых тяжелых ионов в газовых средах.

В настоящей работе представлена компьютерная модель широкого множества газонаполненных сепараторов, построенных на основе дипольных и квадрупольных магнитов. Модель реализована в виде двух компьютерных процедур. Первая основана на расчете матриц перехода в параксиальном приближении и обеспечивает имитационное моделирование на широком множестве ионнооптических схем с минимальными временными затратами на генерирование ионно-оптической схемы и на получение статистики большого объема. Вторая внедрена в пакет SIMION 7.0 и позволяет проводить численное моделирование без ограничений, налагаемых параксиальным приближением при расчете траекторий. В работе приведены примеры расчетов по указанным моделям, которые могут являться основой для усовершенствования ионно-оптических схем трактов газонаполненных магнитных сепараторов.

1. МОДЕЛИРОВАНИЕ ТРАЕКТОРИЙ

Для описания траекторий использовалась стандартная техника статистического моделирования. В ее основу положена микроскопическая модель движения ионов в газовой среде, учитывающая процессы обмена электронами иона с молекулами газа, рассеяние ионов на малые углы в результате многократных столкновений и потери энергии. В этой части работы мы следуем в основном работам [4–6].

В настоящей работе мы не затрагиваем проблем моделирования начальных распределений ионов, которые в газонаполненных сепараторах формируются в результате реакций взаимодействия первичных пучков энергетичных атомов с веществом бомбардируемой ими мишени. Отметим лишь, что эти распределения в типичных случаях отличаются широким зарядовым, энергетическим и угловым распределениями ионов.

1.1. Моделирование флуктуаций ионного заряда в сепараторе

Начальное зарядовое состояние иона после выхода из мишени может быть представлено, например, нормальным распределением

p ( q ) =

exp

V 2 ⁿ°_q

•)

где q_in — средний равновесный заряд ионов, составляющий, как правило, несколько десятков единиц элементарного заряда. Здесь и в дальнейших формулах под зарядом иона q подразумевается (как это принято в литературе, посвященной газонаполненным сепараторам) зарядовое число, т. е. отношение заряда иона к заряду протона. На практике модель начального зарядового распределения не имеет заметного влияния на результат расчетов движения ионов в сепараторе, поскольку трансформация начального зарядового распределения в равновесное распределение для ионов в газе со значениями среднего заряда в несколько единиц реализуется всего за несколько десятков столкновений. Поскольку тяжелый ион при движении в разреженном газе с давлением 1 Торр изменяет свое зарядовое состояние при атомных столкновениях 10²–10³ раз на 1 м пути в зависимости от типа иона и газа [15], то данная релаксация происходит на промежутке в несколько десятков сантиметров. Поэтому, если длина бесполевого промежутка от мишени до первого ионно-оптического элемента сепаратора больше длины релаксации, траектории ионов в сепараторе не зависят от вида начального зарядового распределения.

В качестве промежутка дискретизации траектории принимается случайная величина — длина пробега l между двумя последовательными столкновениями, в которых происходит изменение заряда иона. Длина пробега генерируется в соответствии с соотношением

l = -X In R ,

где R — равномерно распределенное на промежутке [0,1) случайное число. Средняя длина пробега X определяется полным сечением o t процесса изменения заряда и концентрацией n молекул газа

X = 1/( n o t ).

Отметим, что сечение изменения заряда тяжелых ионов при движении в гелии существенно больше сечения при движении в водороде [9]. Средняя длина пробега между столкновениями с изменением заряда для тяжелых атомных ионов

в водороде при давлении 1 Торр составляет порядка 3–5 мм, в гелии эта длина порядка 1 мм.

Представленные в литературе модели обычно ограничиваются учетом одноэлектронных процессов обмена зарядом, т. е. захватом или потерей ионом одного электрона. Как показано в работе [11], в более адекватную модель следует включить процессы захвата ионом одного электрона (сечение процесса a _c ) и процессы потери одного или двух электронов (сечения процессов соответственно a l и a 2 l ), поскольку процессы потери двух электронов приводят к асимметрии равновесных зарядовых распределений, наличие которой отмечалось в экспериментальных исследованиях [12]. В работе [11] было показано, что в случае симметричных зарядовых распределений ионов в пучке флуктуации ионного заряда приводят к увеличению среднего радиуса кривизны траектории иона в магнитном поле. Для зарядовых распределений с асимметрией средний радиус кривизны траектории в магнитном поле может как увеличиваться, так и уменьшаться. Последнее обстоятельство приводит к заметной деформации пространственных распределений ионов в пучке в плоскости дисперсии сепаратора и должно приниматься во внимание при определении начальных настроек сепаратора.

В соответствии с принятой моделью:

a ( q ) = a ( q ) + a ( q ) + a 1 ⁽ q )■            ⁽⁴⁾

Для сечений одноэлектронных переходов, как и в работах [4, 5], у нас используется экспоненциальная аппроксимация:

a ⁽ q ) = A c exp⁽ a c ⁽ q - q o )X           (5)

a(q) = Ai exp(-ai(q - q o)X где q — текущий заряд иона, q0 — величина, которую приближенно можно считать равной среднему равновесному заряду иона q . Такую же аппроксимацию мы используем для сечения потери двух электронов a21(q) = A21 exp(-a 21(q - q0)) -               (6)

Вероятности переходов определяются из соотношений

P c ⁽ q ) = a ⁽ q )/ ^a t ⁽ q ),

P i ⁽ q ) = a ⁽ q V a ⁽ q ),                (7)

p 2 1 ⁽ q ) = ^a 2 1 ⁽ q V a ⁽ q )•

Заметим, что в случае одноэлектронных переходов, когда a _{2 1} = 0, среднее значение равновесного заряда q = q ₀. При учете потери двух электронов средний равновесный заряд увеличивается:

q >  q o .

Значения коэффициентов в формулах (5) и (6) на настоящий момент являются наименее точно известными из всех параметров ионно-молекулярного взаимодействия. Их значения определяются из экспериментальных данных или аппроксимируются, исходя из соответствия данных моделирования и результатов эксперимента (см. раздел 2 настоящей работы).

Скоростная зависимость среднего равновесного заряда зависит от диапазона энергий ионов и атомных номеров ионов и атомов газа. В частности, в случае движения тяжелых атомных ионов в водороде в области скоростей 0.8 <  и / и ₀ <  2.6, где и ₀ = e ²/ h = 2.19 х 10⁸ см /с — боровская скорость, эта зависимость может аппроксимироваться простым выражением, полученным при обработке большого массива экспериментальных данных [13]:

q = 3.26( и / и ₀) - 1.39. (8)

Аппроксимация (8) не содержит зависимости от атомного номера иона Z . Отметим, что существует множество других аппроксимаций, как например предложенная в работе [14]:

q = Z {1 - C , exp[ - C 2 U /( и Z ^Y )]}. (9)

Параметры C1, C2 и / определяются эмпирически для каждого иона и газа. В случае C1 = C2 = 1, / = 2/3 и и/(u0ZY) << 1 соотношение (9) переходит в известную формулу Бора q = — Z1/3. (10)

^U 0

В случае взаимодействия ионов с атомными номерами 36 <  Z <  102 с гелием в области скоростей 1.5 <  и / и ₀ <  4.5 аппроксимация экспериментальных данных [14] дает значения параметров C 1 = 1.04, C ₂ = 0.91, / = 2/3.

Для ионов небольших масс (например, ионов первичного пучка) зависимости (8) и (9) дают неадекватное значение среднего заряда, в некоторых случаях превышающее атомный номер иона. В этом случае реалистическая аппроксимация среднего заряда имеет вид [16]

q « Z { 1 - exp[ - 1.25 X + 0.32 X ² - 0.11 X ³] } , (11)

где X = и [мм/мкс]/(3.6 х 10³ Z ^0.45).

На рис. 1 приведены графики скоростной зависимости среднего равновесного заряда в водороде (формула (8), кривая 1) и в гелии (формула (9) при Z = 102, кривая 2). На этом же рисунке приведены соответствующие скоростные зависимости

B p

а

q

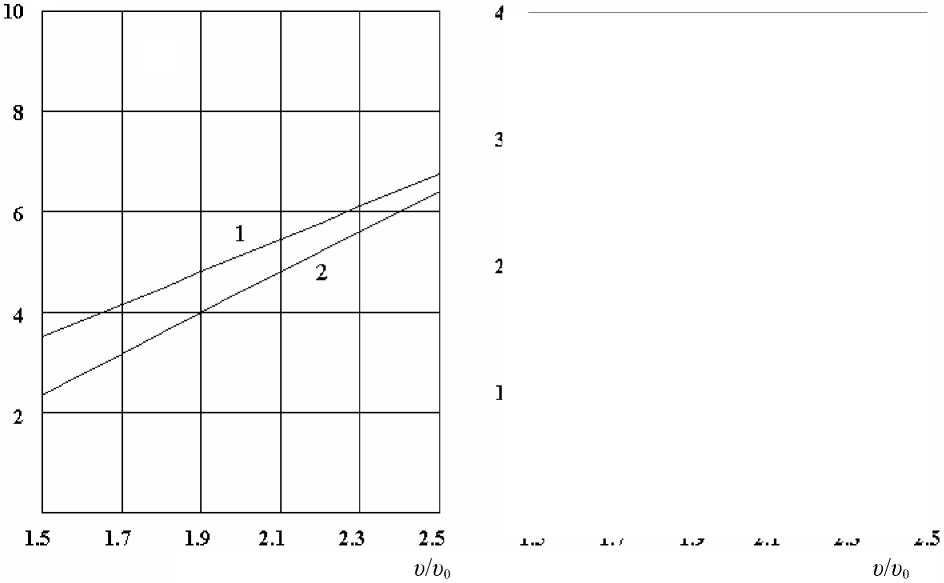
Рис. 1. Скоростная зависимость среднего равновесного заряда q в единицах элементарного заряда (а) и магнитной жесткости B p в единицах [Тл^м] (б) 252 No в водороде в аппроксимации [13] (формула (8), кривые 1) и в гелии в аппроксимации [14] (формула (9), кривые 2)

б

магнитной жесткости. Зависимости демонстрируют убывающий характер — дисперсия магнитной жесткости по скорости отрицательна. Заметим, что для бóровской зависимости (10) эта дисперсия равна нулю, т. е. в приближении (10) наблюдается фокусировка ионов по скорости. Дисперсия магнитной жесткости по скорости (энергии) иона, присутствующая в более реалистичных моделях среднего заряда, вносит значительный вклад в ширину изображения ионного пучка в плоскости детектора газонаполненного сепаратора.

В каждом узле дискретизации траектории производится изменение заряда иона в соответствии с вероятностями (7). В аппроксимирующих выражениях для сечений (5) и (6) в качестве значения q ₀ берется значение среднего равновесного заряда.

• 1.2.    Моделирование углового рассеяния ионов

В принципе длина пробега ионов между двумя столкновениями с молекулами газа меньше расстояния между узлами дискретизации, рассчитываемыми в модели, поскольку не каждое столкновение приводит к изменению заряда иона. Однако в рамках модели многократного углового рассеяния можно производить пересчет направления движения и энергии частицы лишь в каждом узле дискретизации.

В соответствии со стандартно принятой моделью угол отклонения траектории иона в узле дискретизации разыгрывается по нормальному закону

Р ( B ) = J- exP V 2 ПСТ д

- ^

к ^{2 ст} е )

Дисперсия распределения о_в ² пропорциональна длине l отрезка траектории, пройденной ионом между точками дискретизации, и концентрации молекул газа n . Ее численное значение определяется на основе формализма Мейера [17] и Зигмунда [18].

Удобная аппроксимация для полуширины распределения приведенного угла рассеяния предложена в работе [19]:

Д _/2 = 0.92 т ^й56,                     (13)

где

A =__Ea__A • A ^в 1/2             2 ^в 1/2 ; И/2

2 ZZe

— полуширина рас-

пределения угла рассеяния; E — энергия иона; e — элементарный заряд; Z1 и Z2 — атомные номера иона и атома газа соответственно; т = na2nl — приведенная длина отрезка траектории l; a = 0.885a0 (Z2/3 + Z2/3 )"’/2 ; a0 = //'mee2 = = 0.529 x 10-8 см — боровский радиус. Стандартное отклонение распределения (13) может быть оценено по формуле

² 2 Z ₁ Z ₂ e

^U в ~ ^1/2              ^1/2 .

Ea

В грубом приближении для рассеяния тяжелых атомных ионов ( Z ® 100) в водороде при давлении 1 Торр и энергии иона 40 МэВ из формулы (14) можно получить оценку о_в ~ 10 - 4 мм^-1/2.

• 1.3.    Моделирование потерь энергии

Энергия частицы на отрезке траектории длины l уменьшается на величину

A E = sl ,                   (15)

где s = - d E /d x — коэффициент торможения, значения для которого могут быть взяты из таблиц [20]. Скоростная зависимость коэффициента торможения определяется в соответствии с формулой Линдхарда—Шарфа [21], если скорость иона сравнима со скоростями атомных электронов, но не слишком велика ( и <  Z , ^{2 3} и ₀, Z ₁ — атомный номер иона, и ₀ = c /137 = 2.19 x 10⁸см/с — боровская скорость):

s = C_LSn - ,                 (16)

^U 0

или в соответствии с формулой Бете—Блоха [22] для больших значений скорости s = CBBn ^0rln(2 mu2/1),             (17)

u где I — средний потенциал возбуждения атомов среды. Коэффициенты CLS и CBB определяются атомными номерами иона и атомов среды [11]. Для тяжелых атомных ионов в водороде при типичной энергии ионов 40 МэВ и давлении газа 1 Торр можно получить оценку s ~ 1 МэВ/м. Для движения ионов в гелии значение s примерно вдвое меньше.

• 1.4.    Моделирование движения ионов на длине свободного пробега

• 2.    МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ ИОНОВ В ГАЗОНАПОЛНЕННЫХ СЕПАРАТОРАХ

На длине свободного пробега l ионы движутся по траекториям, определяемым магнитным полем элементов сепаратора. Выражения для этих траекторий могут быть взяты в параксиальном приближении, поскольку вклад ионно-оптических аберраций в размеры изображения пучка ионов на детекторе сепаратора значительно меньше вклада, обусловленного взаимодействием с молекулами газа.

НА ОСНОВЕ МЕТОДА МАТРИЦ ПЕРЕХОДА

Представленные в разделе 1 параметризации процессов ион-молекулярных столкновений были использованы при разработке программы расчета газонаполненных сепараторов, основанной на применении метода матриц перехода [23]. Ионнооптическая схема сепаратора представляется в программе последовательностью блоков, каждый из которых относится к определенному типу: бес-полевой промежуток, диафрагма, дипольный магнит, квадрупольный магнит, приемник. Каждому блоку ставится в соответствие свой набор параметров и своя процедура расчета траектории. Такой подход позволяет в рамках единого кода сконфигурировать любую схему, построенную с использованием дипольных и квадрупольных магнитов. Более подробное описание процедуры конфигурирования схемы сепаратора содержится в работе [10].

Расчет отдельной траектории начинается с вызова процедуры генерирования или считывания из файла данных начальных условий движения. Далее для каждой траектории производится последовательный проход по элементам схемы, представленных блоками. Данные, полученные в результате работы программы, хранятся в виде одномерных и двумерных гистограмм распределений частиц по координатам, энергиям и зарядам.

Программа позволяет проводить моделирование траекторий без учета взаимодействия ионов со средой, а также с включением лишь отдельных факторов этого взаимодействия: малоуглового рассеяния, потери энергии, изменения заряда. Это позволяет исследовать вклад каждого из перечисленных факторов в отдельности.

На рис. 2–6 приведены некоторые результаты тестовых расчетов с целью настройки параметров программы и получения данных о влиянии различных факторов на разрешение сепаратора. Ионно-оптическая схема соответствует газонаполненному сепаратору DGFRS Лаборатории ядерных

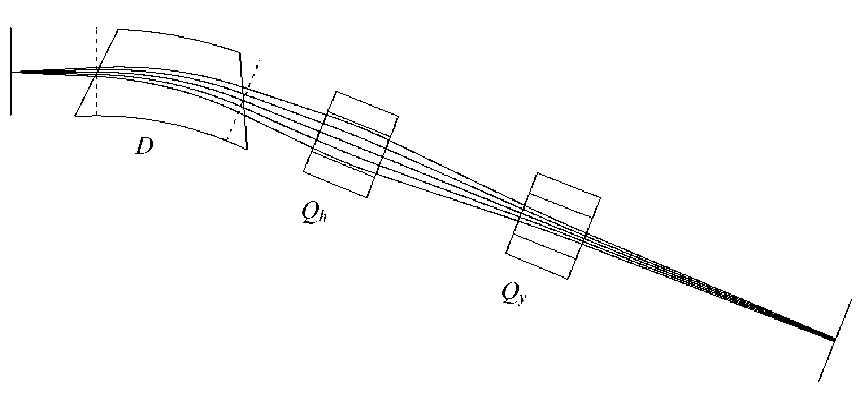
Рис. 2. Ионно-оптическая схема газонаполненного сепаратора DGFRS Лаборатории ядерных реакций ОИЯИ [6] в плоскости дисперсии. Приведены параксиальные траектории ионов без учета взаимодействия со средой

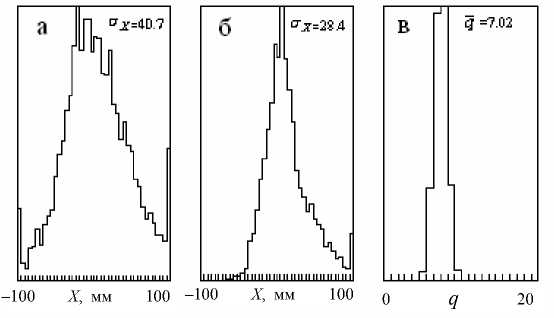
Рис. 3. Гистограммы распределений пучка ионов в плоскости детектора сепаратора по координате X в горизонтальной плоскости (в плоскости дисперсии). а — отключены все процессы взаимодействия со средой, присутствует только начальный энергоразброс — гауссово распределение со средним E ₀ = = 40 МэВ и стандартным отклонением σ E = 5 МэВ, все ионы имеют одинаковый фиксированный заряд; б — включена флуктуация ионного заряда со значениями параметров a c = a l = 2, A c = A l = 1, A 2 l = 0, приводящая к симметричному распределению по ионному заряду q — гистограмма (в)

реакций ОИЯИ [6]. Сепаратор имеет конфигурацию DQ_hQ_y : {дипольный магнит с однородным полем с косым входом и выходом, обеспечивающим фокусировку в вертикальной плоскости (ортогональной плоскости дисперсии)}—{квадруполь-ный магнит с фокусировкой в горизонтальной плоскости}—{квадрупольный магнит с фокусировкой в вертикальной плоскости}. Горизонтальный разрез его ионно-оптической схемы приведен на рис. 2. Здесь же показаны параксиальные траектории ионов без учета взаимодействия со средой. Физические параметры соответствуют ионам ²⁵²No, получающимся в реакции

• ⁴⁸Ca + ²⁰⁶Pb → ²⁵²No + 2n.

Тестовые расчеты показывают следующее.

• 1.    Пространственные распределения пучка ионов в плоскости детектора не зависят от начального зарядового распределения ионов, когда средняя длина свободно г о пробега по отношению к изменению заряда λ ≤ 3мм . При этом ион до входа в магнитное поле дипольного магнита претерпевает не менее ста столкновений.

• 2.    Наблюдается заметное уширение распределения пучка ионов в плоскости детектора по координате в горизонтальной плоскости X (в плоскости дисперсии) с увеличением ширины начального распределения ионов по энергиям (рис. 3, а). Включение процессов флуктуации ионного заряда со скоростной зависимостью среднего равновесного заряда (9) (кривая 2 на рис. 1) приводит к существенному сужению этого распределения (рис. 3, б), Это сужение более сильно выражено со стороны отрицательных значений X , соответст-

• вующих меньшим значениям магнитной жесткости ионов, т. е. большим значениям скорости (см. рис. 1), где отрицательная дисперсия магнитной жесткости по скорости стремится к нулю. При нулевой дисперсии происходит фокусировка ионов по скоростям.

• 3.    Угловое рассеяние ионов в результате многократных столкновений с атомами среды приводит к уширению пучка, примерно пропорциональному величине стандартного отклонения σ_θ в формуле (12) — рис. 4.

• 4.    Пространственные X -распределения (в горизонтальном направлении) пучка ионов в плоскости детектора с ростом коэффициента торможения s ионов в газовой среде при неизменных настройках дипольного магнита сдвигаются в сторону отрицательных значений. Для устранения этого сдвига в программе предусмотрена автоматическая перенастройка магнитных элементов схемы с учетом изменения магнитной жесткости ионов при их торможении.

  

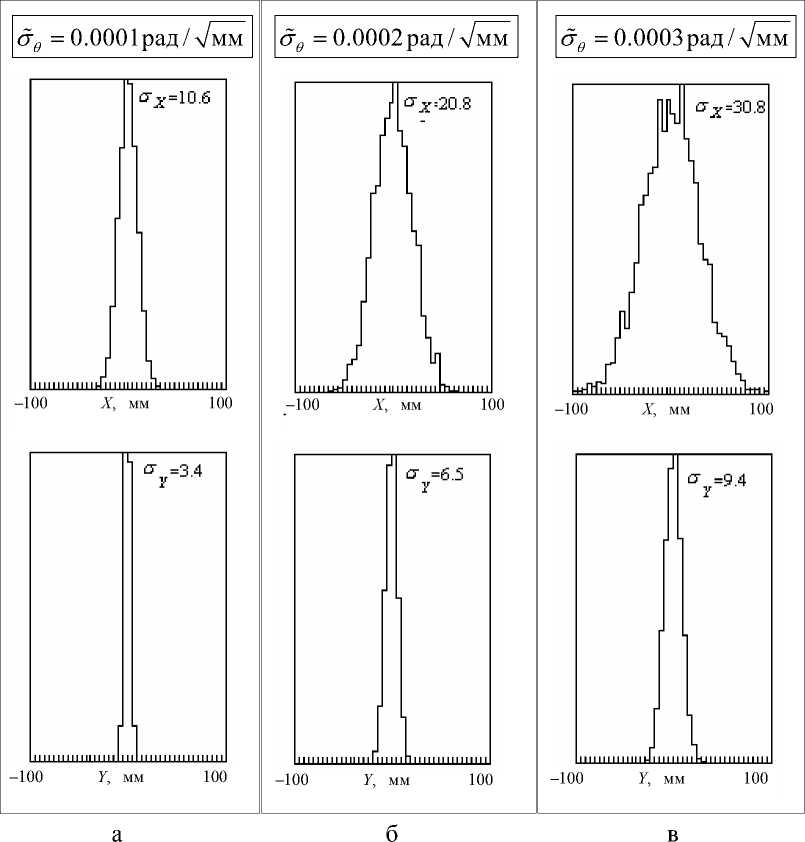
  Рис. 4. Гистограммы распределений моноэнергетического ( σ E = 0) пучка ионов в плоскости детектора в зависимости от интенсивности рассеяния.

  
  

• 5.    При увеличении ширины равновесного зарядового распределения происходит уширение пространственных распределений пучка ионов в плоскости детектора как в горизонтальном, так и в вертикальном (хотя и в меньшей степени) направлениях (рис. 5). Для симметричных зарядовых распределений, когда отключены процессы потери двух электронов, пространственные распределения в горизонтальной плоскости сдвигаются в сторону положительных значений. В этом смысле торможение ионов и флуктуации заряда при симметричных зарядовых распределениях — противоположно действующие факторы. В работе [11] было показано, что в случае симметричных зарядовых распределений ионов в пучке флуктуации ионного заряда приводят к увеличению среднего радиуса кривизны траектории иона в магнитном поле. Для зарядовых распределений с асимметрией средний радиус кривизны траектории в магнитном поле может как увеличиваться, так и уменьшаться.

• 6.    При включении всех ф изических процессов со значениями параметров 1 = 3 мм, о _Е = 3 МэВ,

  s = 1000 эВ/мм, <7 _д = 0.0001 мм ^1/2, a c = a l = a ₂ l = 1, A c = A l = 1, A 2l = 0.2 приведенные на рис. 6 пространственные распределения удовлетворительно аппроксимируют экспериментальные данные, полученные на сепараторе в Дубне [6].

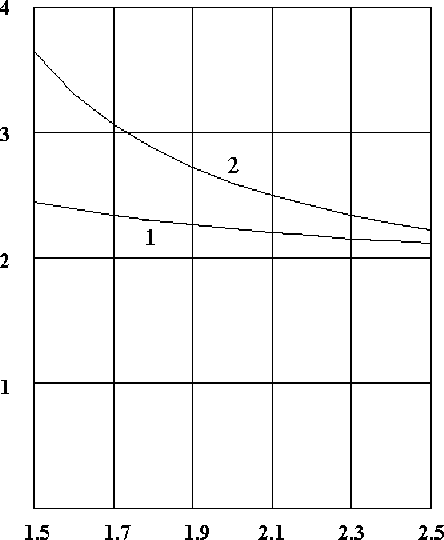
• 7.    Зависимости от давления p ширины пространственных распределений пучка ионов в плоскости детектора в горизонтальном и вертикальном направлениях, представленные на рис. 7, демонстрируют наличие минимума. При низких давлениях пучок уширяется за счет флуктуаций ионного заряда и отклонения зарядового распределения от равновесного. При высоких давлениях усиливается угловое рассеяние пучка при многократных столкновениях с молекулами газа, усиливается торможение ионов и, как следствие, уменьшается средний равновесный заряд ионов, что приводит к усилению негативной роли флуктуаций ионного заряда.

  

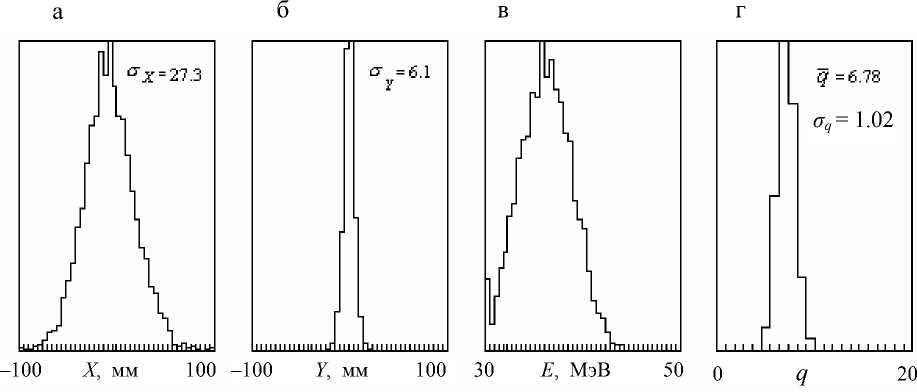
  Рис. 6. Гистограммы распределений пучка ионов в плоскости детектора:

  а — по координате в горизонтальной плоскости X (в плоскости дисперсии); б — по координате в вертикальной плоскости Y ; в — по энергии E ; г — по ионному заряду q . Включены все рассматриваемые процессы

  
  
  

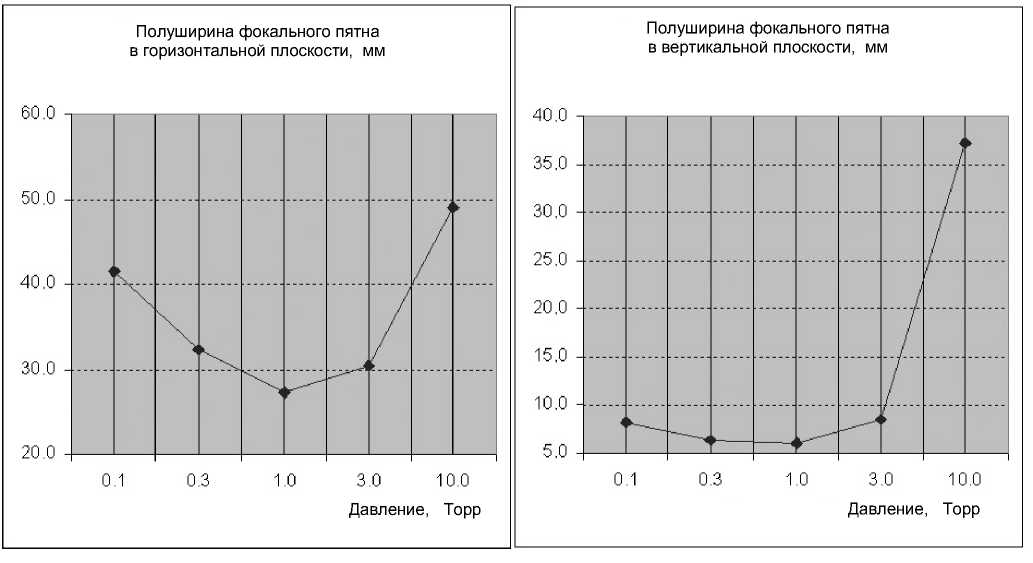
  Рис. 7. Зависимость от давления p стандартных отклонений о X и O Y пространственных распределений пучка ионов в плоскости детектора в горизонтальной и вертикальной плоскостях соответ с твенно. Включены все рассматриваемые процессы. Зависимыми от давления являются параметры Я = 3 p 0 / p (мм), с ~ _в = 0.0001 ^p / p ₀ (мм^-1/2), $ = 1000 p / p ₀ (эВ/мм). При p = p ₀ = 1 Торр значения параметров соответствуют значениям, аппроксимирующим экспериментальные данные, полученные на сепараторе в Дубне [6]

  
  

• 3.    МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ ИОНОВ В ГАЗОНАПОЛНЕННЫХ СЕПАРАТОРАХ

Варьируется (а, б, в) σ ^~ _θ — стандартное отклонение σ _θ в формуле (12), приведенное к промежутку l = 1 мм (величина указана на поле рисунка). Отключены процессы потери энергии ( s = 0) и флуктуации заряда

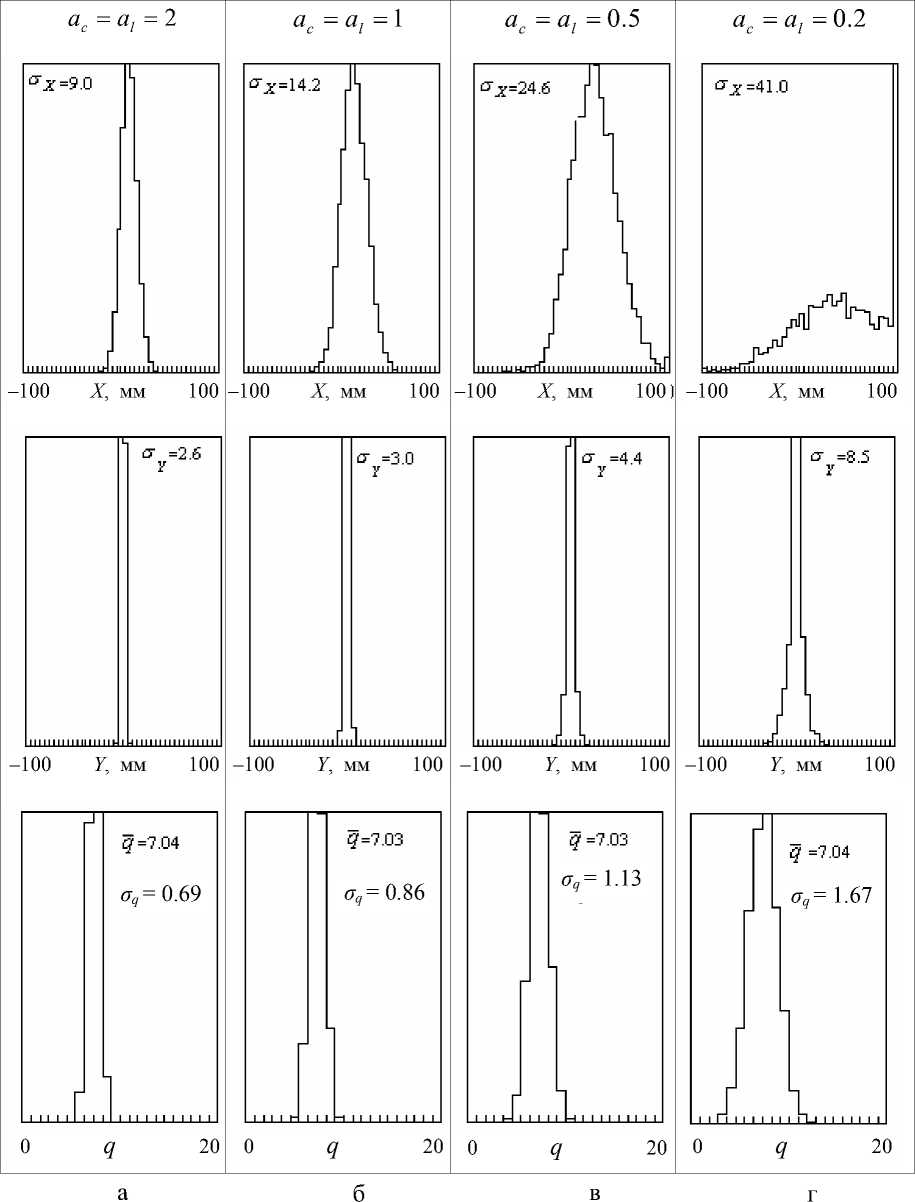
Рис. 5. Гистограммы распределений моноэнергетического ( σ E = 0) пучка ионов в плоскости детектора в зависимости от параметров флуктуации ионного заряда.

Варьируются (а, б, в, г) a_c , a_l при фиксированных значениях A_c = A_l = 1 , A _{2 l} = 0 . Отключены процессы потери двух электронов, торможения ( s = 0) и рассеяния ионов

НА ОСНОВЕ ПРОГРАММЫ SIMION

Альтернативной реализацией расчета представленных в разделе 1 параметризаций процессов в газонаполненных сепараторах является программа моделирования, выполненная на основе компьютерного пакета SIMION 7.0 [24]. С целью учета процессов ион-молекулярных взаимодействий для этого пакета была написана пользовательская программа, включающая разыгрывание случайных процессов столкновений ионов с молекулами газа, торможения ионов, углового рассеяния и перезарядки ионов. Поля магнитов в программе рассчитывались в приближении бесконечной магнитной проницаемости ферромагнитных элементов их конструкций.

Преимуществом моделирования на основе программы SIMION является отсутствие ограничений, связанных с параксиальным приближением расчета траекторий ионов между столкновениями. В частности, это позволяет более реалистично описывать поведение ионов с магнитной жесткостью, сильно отличающейся от жесткости, на которую настроен прибор (ионов первичного пучка), а также фокусировку ионов с большими значениями относительного энергоразброса (см. пример ниже). Дополнительным преимуществом является удобство визуализации ионных траекторий, включая результаты процесса столкновений.

В целом результаты расчетов пропускания сепаратора и степени очистки ионов от нежелательных примесей, выполненных по указанной программе, и расчетов, выполненных с применением матричного метода (см. раздел 2), совпадают с хорошей точностью.

В качестве примера визуализации программой SIMION ионно-оптических систем газонаполненных сепараторов ионов на рис. 8 приведено трехмерное изображение геометрии масс-сепаратора DGFRS Лаборатории ядерных реакций ОИЯИ [6] и двумерные проекции пучка ионов продукта реакции слияния 30Si + 244Pu → 271Hs + 3n при толщине плутониевой мишени 0.4 мг/см2 на плоскость дисперсии сепаратора и перпендикулярную ей плоскость.

Квадрупольный магнит

Дипольный магнит

Детектор

Квадрупольный магнит

б

в

Пучок ионов в плоскости дисперсии

Пучок ионов в плоскости, перпендикулярной плоскости дисперсии

Рис. 8. Трехмерная визуализация (а) геометрии сепаратора DGFRS Лаборатории ядерных реакций ОИЯИ [6] программой SIMION и фокусировка пучка ионов в плоскости дисперсии (б) и перпендикулярной ей плоскости (в) при моделировании пропускания продукта реакции ³⁰Si + ²⁴⁴Pu → ²⁷¹Hs + 3n. Толщина плутониевой мишени 0.4 мг/см²

На рис. 9 изображено соответствующее расчетное распределение ионов в плоскости детектора. Рассматриваемая асимметричная реакция создает экстремальные начальные условия для сепаратора, поскольку характеризуется низкой средней энергией выхода ионов из мишени (около 13 МэВ) и очень большим 70 %-м энергоразбросом ионов, становящимся почти 100 %-м на выходе сепарато- ра из-за торможения ионов в газе (Н2). Значительное расширение пучка ионов в бесполевом пространстве перед детектором обусловлено в основном этим энергоразбросом. Начальный угловой разброс ионов в конус с углом полураствора, большим 10°, приводит к отсечке существенной части пучка анализатором прежде всего за счет узкого межполюсного зазора дипольного магнита.

• -4° -|----------------1----------------1----------------1----------------1----------------1----------------1----------------1----------------1----------------1----------------1----------------1----------------1

• -150       -100        -50         0          50         100        150

• X , мм

Рис. 9. Расчетное распределение попаданий ионов продукта реакции ³⁰Si + ²⁴⁴Pu → ²⁷¹Hs + 3n при толщине плутониевой мишени 0.4 мг/см² на плоскость детектора

ЗАКЛЮЧЕНИЕ

Представленные в работе алгоритмы и программы расчета свойств газонаполненных магнитных масс-сепараторов позволяют учесть все процессы взаимодействия ионов с молекулами газа в ионно-оптических трактах и адекватно моделировать пропускание и разрешающую способность таких сепараторов в широком диапазоне их геометрий и исследуемых продуктов реакций при условии использования внешних процедур моделирования начальных условий для пучков ионов, выходящих из мишени сепаратора. Это открывает возможность для сравнительного анализа ионнооптических схем газонаполненных сепараторов и синтеза схем сепараторов нового поколения.