Численное моделирование формы мениска расплава в индукционной тигельной печи с использованием открытого программного обеспечения

Расплавленный металл в электромагнитном поле индукционной тигельной печи (ИТП) под воздействием радиальной составляющей объемных сил Лоренца f л начинает движение, образующее мениск на свободной поверхности расплава (рис. 1). Формирующаяся естественная двухконтурная электродинамическая циркуляция расплава имеет как положительные – выравнивание температуры и химического состава, химическое взаимодействие металла со шлаком, – так и отрицательные свойства – прорыв окисной пленки, неэффективное использование шлаков, сравнительно слабое смешивание циркулирующих контуров и пр. [1–3].

Выделим уже известные зависимости для мениска в ИТП: высота мениска растет при увеличении удельной мощности; при неизменной мощности, передаваемой в расплав, силовое воздействие на него усиливается с понижением частоты [2]. Также известно, что выраженность мениска будет зависеть не только от электромагнитных (ЭМ), но и от геометрических параметров ЭМ-системы, а именно от положения торца катушки относительно поверхности расплава, от расстояния между расплавом и катушкой [1, 2].

Исследования мениска проводились с помощью аналитических методов [1, 2], одномерными численными моделями без учета гидродинамики [4], двухмерными осесимметричными численными моделями с учетом гидродинамики [5], а также с использованием современного мениск

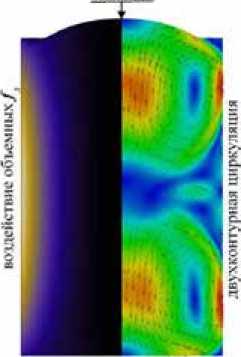
Рис. 1. Формирование мениска в тигле индукционной печи

Fig. 1. The formation of the meniscus in the crucible of an induction furnace программного обеспечения с доработками для связывания ЭМ и гидродинамических задач: Ansys classic + CFX [6], Ansys classic + Ansys fluent [7], Elmer + OpenFOAM [8] и Comsol + Ansys fluent [9]. Свободная поверхность расплава в переменном электромагнитном поле является МГД-задачей, относящейся к разряду комплексных физических задач. Для решения такого типа задач предложено использование открытой библиотеки EOF-Library [10], поскольку она обладает рядом преимуществ перед остальными связками решателей: имеет открытый исходный код, распространяется бесплатно и позволяет выполнять связку двух решателей параллельно, без дополнительных программ, которые увеличивают время расчета.

Целью данной работы служит выявление основных закономерностей формирования мениска на свободной поверхности эвтектического сплава GaInSn в электромагнитном поле (ЭМП) ИТП. Теоретический эксперимент проводили на математической модели МГД-процессов, решаемой численным методом с помощью открытой библиотеки EOF-Library. Исследование зависимостей параметров мениска от энергетических и геометрических параметров позволило оценить возможности и выполнить отладку созданных моделей.

Описание расчетной системы

При исследованиях электромагнитных процессов в ИТП рассматривается система «индуктор – загрузка». Индуктор в зависимости от энергетических параметров системы может быть выполнен в виде многовитковой катушки переменного тока с естественным воздушным охлаждением или в виде массивной трубки с принудительным водяным охлаждением. Загрузкой в случае применения непроводящего тигля или тигля прозрачного для ЭМП на данных частотах является только расплав.

Для численного решения были приняты следующие допущения: витки реального индуктора заменяют одним витком с соответствующей магнитодвижущей силой (МДС); непроводящие и незначительные геометрические элементы конструкции не учитываются; задача решается в двухмерной осесимметричной постановке; поле в электромагнитной задаче изменяется по гармоническому закону; тепловыми процессами и естественным конвективным движением расплава пренебрегается. Допущения являются стандартными для данного класса задач и не приводят к значительному увеличению отклонения результатов, однако позволяют значительно сэкономить вычислительные ресурсы. Схематичное представление геометрии расчетной области с основными размерами показано на рис. 2, где 1 - расплав, 2 - индуктор. Размеры брали в масштабах физической модели индукционной тигельной печи для изучения МГД-явлений на низкотемпературном эвтектическом сплаве с металлической проводимостью.

Гидродинамическую задачу решали только в области расплава. Ожидаемое число Рейнольдса в расплаве Re ≈ 38 000, что много больше критического значения, и следует ожидать образование турбулентных течений. Их учет производили с помощью k-s -модели турбулентности. В условиях переменного магнитного поля в гидродинамической задаче учитывали силовое воздействие через дополнительный источник движения. Моделирование свободной поверхности реализовано с помощью метода объема жидкости (VOF ), где а характеризует объемную долю жидкости в ячейке сетки.

Электромагнитную задачу решали в квазистационарной постановке, с указанием эквивалентной плотности тока. Расчетная область, помимо индуктора и загрузки, заполнена возду-

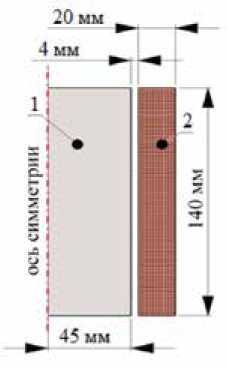
Рис. 2. Геометрия расчетной области

Fig. 2. Geometry of the computational domain

Таблица 1. Физические свойства материалов

Table 1. Physical properties of materials

п/п Параметр Обозначение Единицы измерения Величина Расплав GaInSn 1 Плотность ρ кг/м3 6080 2 Проводимость σ См/м 3.85×106 3 Кинематическая вязкость ν м2/с 2.6315×10-7 Медный индуктор 4 Относительная магнитная проницаемость          µ о.е. 1 5 Проводимость σ См/м 5.96×107 Окружающая среда – воздух 6 Плотность ρ кг/м3 1 7 Кинематическая вязкость ν м2/с 1.48×10-5 8 Поверхностное натяжение расплав – воздух         γ Н/м 0.72 хом, границы которого в электромагнитной задаче удалены от индуктора для снижения влияния граничных условий.

Во время расчета МГД-задачи пересчет ЭМ-части инициировался в зависимости от изменения положения свободной поверхности, определяемой в ходе решения гидродинамической части. Такой подход позволяет сократить количество внутренних решений электромагнитной части, за счет чего сильно сокращается общий объем вычислений. Далее по тексту и на графиках для обозначения величины МДС используется полный ток I, A ∙ вит . Все результаты исследования, связанные с границей раздела сред, будут показаны для α = 0,5. В результатах представлен установившийся режим нестационарного расчета указанной МГД-задачи. Свойства используемых материалов, необходимые для решения МГД-задачи, представлены в табл. 1.

Исследование формы мениска в зависимости от энергетических и геометрических параметров

Определение зависимостей, связывающих параметры ИТП и форму мениска, потребовало ввести следующие оценочные параметры: общая высота мениска Δ h = h max – h min , где h max , h min – максимальное и минимальное осевое положение мениска; отклонение мениска от положения равновесия Δ h 0 = h max – h 0 , где h 0 – начальный уровень расплава (рис. 3 а ); U cp , – средняя скорость циркуляции расплава.

Данные параметры позволили охарактеризовать наблюдаемые процессы в расплаве с точки зрения гидродинамики. По мере проведения численного эксперимента варьировались два ЭМ параметра системы – частота питания индуктора f 0 и полный ток I , а также наполненность тигля расплавом. Рассмотрим зависимость оценочных параметров от полного тока, представленную на рис. 3 б .

На рис. 3 б наблюдается квадратичная зависимость высоты мениска (Δ h ) от тока и, соответственно, линейная зависимость от мощности системы. Средняя же скорость ( U cp ) линейно связана с величиной тока.

На рис. 4 представлена зависимость оценочных параметров от относительной глубины проникновения d'-l/fR^rf^ , где R – радиус расплава, μ₀ – магнитная постоянная; σ – проводимость расплава; f 0 – частота питания индуктора.

Увеличение частоты питания индуктора (уменьшение Δ' ) дает монотонный рост интегрального значения сил Лоренца F Л , что отражается увеличением всех оценочных параметров. Когда глубина проникновения становится близкой к радиусу заготовки (для используемых в расчете размеров порядка 500 Гц), рост электромагнитного давления вызывает увеличение гидростатического давления для уравновешивания системы, что видно из отклонения мениска от положения равновесия (Δ h 0 ). Скорости расплава ( U cp ) зависят от величины F Л , в то время как параметры свободной поверхности и силы Лоренца имеют более сложную взаимосвязь. Форма мениска зависит от величины, однако локальный характер распределения сил F Л , а именно осевое распределение в зоне мениска из-за проявления краевого эффекта, имеет большее влияние на свободную поверхность, что характеризуется разными значениями Δ' максимумов

а )

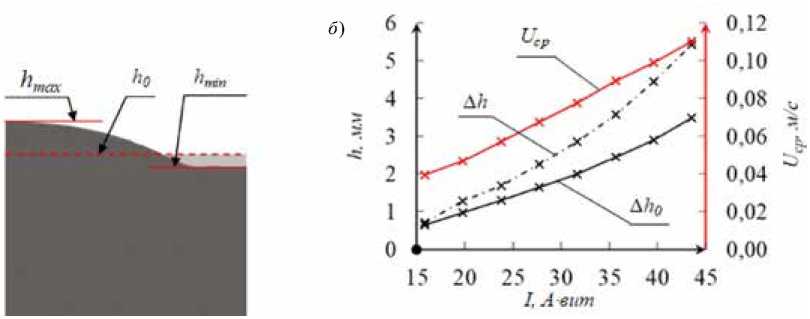
Рис. 3. Осевые положения мениска ( а ); зависимость оценочных параметров от полного тока ( б )

Fig. 3. Axial position of the meniscus ( а ); dependence of estimated parameters on the total current ( б )

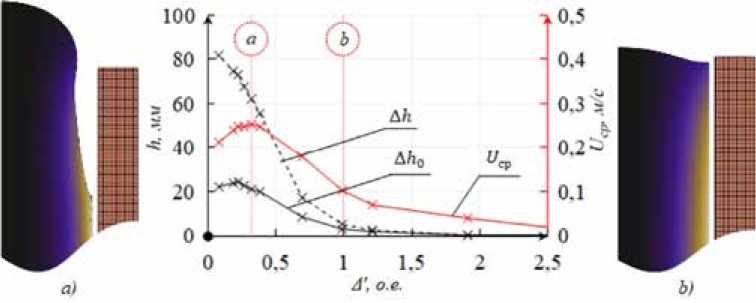
Рис. 4. Зависимость оценочных параметров от относительной глубины проникновения

Fig. 4. The dependence of the estimated parameters on the relative depth of penetration указанных параметров. Дальнейшее увеличение частоты приводит к снижению интегрального значения, но к увеличению плотности сил Лоренца, чем можно объяснить различие в характере поведения параметров Δh0 и Δh в данном диапазоне частот. Такой характер увеличения высоты мениска (Δh) объясняется тем, что снижение точки мениска hmin связано с увеличением ЭМ-давления в пограничном слое на поверхность расплава вплоть до полного отрыва расплава от стенок тигля.

Для обозначения наполненности тигля расплавом относительно индуктора введен параметр k m = h 0 / h ind , где h ind – высота индуктора, и выполнен анализ его влияния на характеристики мениска (рис. 5).

При опустошении тигля k m < 1 (рис. 5 а ) высота мениска будет увеличиваться, это объясняется возрастанием осевой составляющей силы Лоренца из-за краевых эффектов. Создаваемое дополнительное давление на свободную поверхность около точки контакта трех сред (воз-

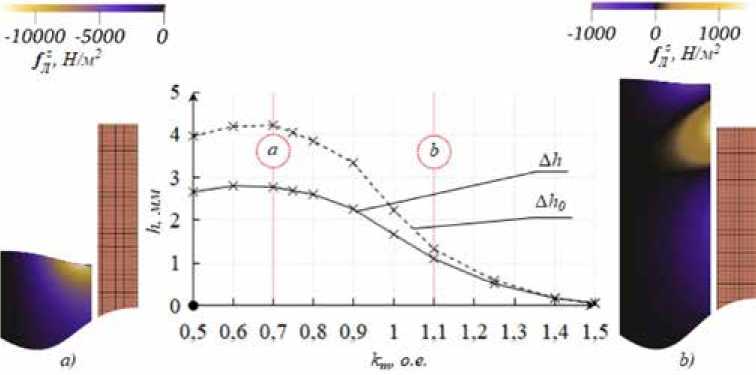
Рис. 5. Зависимость оценочных параметров от наполненности тигля расплавом

Fig. 5. The dependence of the estimated parameters on the filling of the crucible with the melt дух-расплав-тигель), усиливает верхний контур циркуляции и увеличивает высоту мениска. Дальнейшие опустошение тигля приводит к незначительному снижению высоты мениска из-за ограничения общего объема расплава для замыкания гидродинамических течений. При переполнении тигля km > 1 (рис. 5b) исчезает осевая составляющая электромагнитных сил и вместе с ней мениск. Из [1] также известно, что в данной зоне возможно формирование вторичных течений над индуктором.

Заключение

Результаты нестационарного расчета созданных моделей после отладки коррелируют с верифицированными результатами, проведенными в авторитетных работах по данным направлениям, что говорит о достаточной достоверности модели при сохранении ее преимуществ перед остальными способами сопряженного численного решения МГД-задач.

Полученные результаты позволили выбрать базовые значения основных параметров системы для дальнейшего решения нестационарной задачи, направленной на изучение переходных и колебательных гидродинамических процессов.

Проведенный анализ выполненных исследований с учетом гидродинамики дополняет задачу свободной поверхности в электромагнитном поле. В частности, анализ положения катушки относительно поверхности расплава дает более полное представление о формировании мениска, что может быть использовано для более эффективного проведения плавки различных металлов и сплавов в холодном тигле с учетом технологических требований и ограничений. Также возникает возможность проведения исследований локального воздействия на свободную поверхность расплава с целью управления формой мениска и характером локальных течений, что позволит исключить отрицательные свойства связанных явлений в индукционной тигельной печи.

Благодарность / Acknowledgement

Исследование выполнено при финансовой поддержке РФФИ и Правительства Красноярского края в рамках научного проекта № 18-48-242013 «Исследование влияния пространственных и частотно-временных распределений электромагнитных сил в расплаве на характер протекания МГД-процессов в жидком металле».

No. 18-48-242013 «Study of the influence of spatial and frequency-time distributions of electromagnetic forces in the melt on the nature of the course of MHD processes in liquid metal.»