Численное моделирование гибридных систем явным методом третьего порядка в инструментальной среде ИСМА
Автор: Новиков Антон Евгеньевич, Новиков Евгений Александрович, Шорников Юрий Владимирович, Достовалов Дмитрий Николаевич
Журнал: Проблемы информатики @problem-info
Рубрика: Математическое и имитационное моделирование сложных систем
Статья в выпуске: 3 (7), 2010 года.
Бесплатный доступ
На основе трехстадийной схемы типа схемы Рунге - Кутты третьего порядка точности разработан ал- горитм переменного шага. Построены неравенства для контроля точности вычислений и устойчивости численной схемы. Для гибридных систем разработан алгоритм выбора шага интегрирования с учетом событийной функции.
Метод рунге - кутты, контроль точности и устойчивости, переменный шаг, гибридные задачи
Короткий адрес: https://sciup.org/14320036
IDR: 14320036 | УДК: 519.622
Текст научной статьи Численное моделирование гибридных систем явным методом третьего порядка в инструментальной среде ИСМА
Введение. Для большого количества технических задач характерно наличие событий, которые означают наличие точек разрыва в первых производных от фазовых переменных. Такие комбинированные дискретно-непрерывные системы называются гибридными, или системами с переключением [1–3]. В них события происходят в моменты времени, соответствующие нулям некоторой алгебраической функции. Во многих случаях проблема усугубляется большой размерностью и жесткостью рассматриваемой задачи. При решении жестких задач большой размерности основные вычислительные затраты приходятся на декомпозицию матрицы Якоби [4–6], поэтому эффективность алгоритма интегрирования обычно повышается за счет замораживания матрицы Якоби [7]. В случае умеренно жестких задач можно применять алгоритмы интегрирования на основе явных методов с контролем точности вычислений и устойчивости численной схемы [8].
В данной работе создан алгоритм интегрирования переменного шага на основе трехстадийной схемы типа схемы Рунге – Кутты третьего порядка точности. Построены неравенства для контроля точности вычислений и устойчивости численной схемы. Алгоритм интегрирования может быть использован при решении гибридных задач, в том числе умеренно жестких. Разработан также алгоритм обнаружения событий гибридной системы. Рассмотренные
Работа выполнена в рамках АВЦП “Развитие научного потенциала высшей школы (2009-2010 гг.)” (код проекта РНП 2.1.2/4751), ФЦП “Научные и научно-педагогические кадры инновационной России” на 2009-2011 гг. (государственный контракт № П-297), а также при финансовой поддержке РФФИ (код проекта 08-01-00621) и Совета по грантам Президента РФ для государственной поддержки ведущих научных школ РФ (грант № НШ-3431.2008.9).
методы реализованы в среде моделирования гибридных систем ИСМА (инструментальные средства машинного анализа) [9].
1. Трехстадийный метод типа метода Рунге – Кутты. При численном решении задачи Коши для системы обыкновенных дифференциальных уравнений
У = f ( У ) , У ( 1 0 ) = У 0 , 1 0 < t < t k (1)
рассмотрим явный трехстадийный метод типа метода Рунге – Кутты вида
Уп+1 = Уп + P1 k 1 + P 2 k 2 + P з k з, k 1 = hf (Уп), k 2 = hf (Уп + в 21 k 1), (2)
k 3 = hf ( Уп + в31k 1 + в32 k 2), где y и f — вещественные N -мерные вектор-функции; t — независимая переменная; h — шаг интегрирования; k1 ,k2 и k3 — стадии метода; p1, p2, p3, β21, β31 и β32 — числовые коэффициенты, определяющие точность и устойчивость (2). В случае неавтономной системы y' = f (t, У), У (t0) = У0, 10 < t < tk, схема (2) записывается в виде
Уп+1 = Уп + P1 k 1 + P 2 k 2 + P 3 k 3, k 1 = hf (tn,Уn), k2 = hf (tn + в21 h, Уп + в21 k 1), k3 = hf(tn + [в31 + в32]h, Уп + в31k 1 + в32k2).
Ниже для упрощения выкладок будем рассматривать задачу (1). Однако разработанные методы можно применять для решения неавтономных задач.
Получим соотношения, определяющие коэффициенты метода (2) третьего порядка точности. Для этого разложим стадии k 1 ,k 2 и k 3 в ряды Тейлора по степеням h до членов с h 4 включительно и подставим в первую формулу (2). В результате получим
У п +1 = У п + ( P 1 + P 2 + P 3 ) hf + [ в 21 P 2 + ( в 31 + в 32 ) P 3 ] h 2 f n f n +
+ h 3 [ в 21 в 32 P 3 У п 2 f n + 0 , 5( в 21 P 2 + ( в 31 + в 32 ) 2 P 3 ) /""^ 2 ] +
+ h 4 [0 , 5 в 21 в 32 P 3 f ' f ' fn + в 21 ( в 31 + в 32 ) в 32 P 3 f '' f ' f 2 +
+ {[ в21P 2 + ( в31 + в32)3 P 3] / 6 }f'"f3] + O ( h5), где элементарные дифференциалы вычислены на приближенном решении y .
Точное решение y ( t п +1 ) в окрестности точки t,1 можно представить в виде
У(tn+1) = У(tn) + hf + 0, 5h2f'f + (h3/6)[f'2 f + f''f 2] + + (h 4 / 24)[ f'3 f + 3 f ''f 'f 2 + f 'f ''f 2 + f '"f3] + O (h 5), где элементарные дифференциалы вычислены на точном решении y (t.^). Сравнивая ряды для приближенного yп+1 и точного y (tп+1) решений до членов с h3 включительно при условии Уп = У(tn), запишем условия третьего порядка точности схемы (2):
-
1) P 1 + P 2 + P 3 = 1;
-
2) в 21 p 2 + ( в 31 + в 32 ) p 3 = 1 / 2;
-
3) в 21 p 2 + ( в 31 + в 32 ) 2 p 3 = 1 / 3;
-
4) в 21 в 32 Р 3 = 1 / 6 •
В предположении y n = y ( t n ) локальную ошибку 5 п схемы (2) можно вычислить по формуле 5 n = y ( t n +1 ) — y n +1 . Учитывая представления y ( t n +1 ) и y n +1 в виде рядов Тейлора, получаем
S n = h 4 [ f 0; f 0 3 f + f — — 9 в 21 в 32 p 3^) f 0 f 00 f 2 + ( 7 — в 21 в 32 ( в 31 + в 32 ) p 3^) f"/ 0 f 2 +
24 у 24 2 у у 8 у
+ Гт7 — 7 в 21 p 2 — 7( в 31 + в 32 ) 3 p 3 ^ f 000 f 3 ] + O ( h 5 ) •
У 24 6 6
В нелинейной системе условий третьего порядка точности численной схемы имеется два свободных коэффициента. Положим в 21 = 0 , 5 и в 31 + в 32 = 1 • Тогда на каждом шаге к 1 , к 2 и к 3 вычисляются в точках t n , t n + 0 , 5 h и t n + h соответственно. Условия третьего порядка запишем в следующем виде:
-
1) Р 1 + Р 2 + Р 3 = 1;
-
2) 0 , 5 p 2 + p 3 = 1 / 2;
-
3) 0 , 25 p 2 + p 3 = 1 / 3;
-
4) в 32 p 3 = 1 / 3 •
-
6 . = 24 h 4 / 0 3 / — /”/ 0 / 2 — 3 / 000 / 3) = O ( h 5 ) •
Из второго и третьего уравнений данной системы находим p 2 = 2 / 3 и p 3 = 1 / 6. Из первого и последнего уравнений получаем p 1 = 1 / 6 и в 32 = 2 • Из равенства в 31 + в 32 = 1 следует в 31 = — 1. В результате коэффициенты метода (2) имеют вид
p 1 = p 3 = 7 , p 2 = 7 , в 21 = 7 , в 31 = — 1 , в 32 = 2 • 63 2
При данных соотношениях локальную ошибку 5 n схемы (2) можно записать следующим образом:
Построим неравенство для контроля точности вычислений метода третьего порядка. Для этого рассмотрим вспомогательную схему
-
У п +1 , 1 = У п + r 1 к 1 + r 2 к 2 ,
где k 1 и k 2 определены в (2). Потребуем, чтобы данный метод имел второй порядок точности. Сравнение рядов для y ( t n +1 ) и y n +1 , 1 показывает, что требование второго порядка будет выполнено, если r 1 + r 2 = 1 и в 21 r 2 = 0 , 5 • Отсюда и из (3) получаем r 1 = 0 и r 2 = 1. С использованием идеи вложенных методов ошибку Е п, 3 метода третьего порядка можно оценить по формуле
£ п, 3 = y n +1 — y n +1 , 1 = ( p 1 — r 1 ) к 1 + ( p 2 — r 2 ) к 2 + p 3 к 3 •
Тогда неравенство для контроля точности вычислений имеет вид
||k 1 — 2 к 2 + k 3 || < 6 E, где || • || — некоторая норма в RN; e — требуемая точность расчетов.
Построим неравенство для контроля устойчивости (2) предложенным в [8] способом. Запишем стадии к 1, к2 и к3 применительно к задаче у0 = Ay, где A — матрица с постоянными коэффициентами. Используя соотношения (3), в результате получим к 1 = Xyn, к 2 = ( X + 0,5 X 2) Уп, к 3 = [ X + X2 + X 3] Уп, где X = hA. Найдем коэффициенты d 1, d2 и d3 из условия выполнения равенства d 1 к 1 + d 2 к 2 + d з к 3 = X3 Уп.
Данное требование будет выполнено, если d 1 = d 3 = 1 и d 2 = — 2 . Нетрудно заметить также, что к 2 — к 1 = X 2 y n . Тогда согласно [8] оценку максимального собственного числа v n, 3 = hX max матрицы Якоби системы (1) можно вычислить по формуле
V n 3 = 0 , 5 max ( \к\ — 2 к ^ + к | \/к — кЦ ) . (4)
1 ≤i≤N 1 2 3 2 1
Функция устойчивости Q(x) метода (2) с коэффициентами (3) имеет вид Q(x) = 1 + x + x2/2 + x3/6. Область устойчивости схемы (2), построенная в среде ИСМА [9, 10], приведена на рис. 1. Построены линии уровня |Q(x) | = q при q = 0,05; 0,30; 0,70; 1,00. Интервал устойчивости численной формулы (2) приблизительно равен 2,5, поэтому для контроля ее устойчивости можно использовать неравенство vn, 3
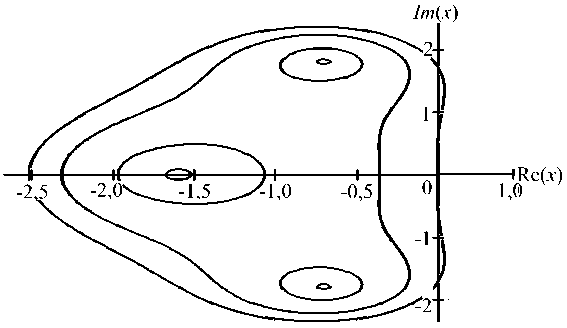
Рис. 1. Область устойчивости трехстадийного метода (2) третьего порядка точности
-
< 2 , 5.
-
2. Гибридная система. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений вида
Полученная оценка (4) является грубой, поскольку максимальное собственное число необязательно значительно отделено от остальных, в степенном методе применяется небольшое количество итераций, дополнительные искажения вносит нелинейность задачи (1). Поэтому в данном случае контроль устойчивости используется как ограничитель на размер шага интегрирования. В результате прогнозируемый шаг h n +1 вычисляется следующим образом.
Новый шаг по точности hac определим по формуле hac = q 1 hn, где hn — последний успешный шаг интегрирования; q 1 задается уравнением q3||еп, 31| = E с учетом соотношения En,3 = O(hn). Шаг по устойчивости hst зададим формулой hst = q2hn, где q2 определяется из уравнения q2vn, 3 = 2,5 с учетом равенства vn, 3 = O (hn). В результате прогнозируемый шаг hn+1 вычисляется по формуле hn+1 = max[hn, min(hac, hst)].
Данная формула позволяет стабилизировать поведение шага на участке установления решения, где определяющую роль играет устойчивость. Именно наличие данного участка существенно ограничивает применение явных методов при решении жестких задач.
y = f ( y ) , y ( t 0 ) = y о , g ( y,t ) < о ,
где g (y, t) — событийная функция или нелинейный предохранитель. Поскольку многие модели, представляющие интерес, линейны, будем рассматривать их как наиболее важный класс событийных функций. Заметим, что любой нелинейный предохранитель можно привести к линейному виду добавлением дополнительной фазовой переменной x = g (y, t). В результате задачу (5) можно записать в виде y0 = f(У), x = ^f(У) + Ig, x < 0 • ∂y ∂t
Здесь принимается, что событийная функция линейна. Также для упрощения рассуждений будем предполагать, что исходная задача скалярная. Однако все приведенные ниже выводы будут распространяться и на системы уравнений. Особое внимание следует уделить выбору метода интегрирования. Полностью неявный метод использовать нельзя, поскольку он требует вычисления f (y) в потенциально опасной области, где модель не определена. В то же время известно, что явные методы слабоустойчивы. Поэтому будем использовать построенный выше метод (2) с контролем точности вычислений и устойчивости численной схемы. В этом случае событийная динамика описывается соотношением gn +1 g (yn +1, tn + hn+1), где yn+1 вычисляется по формуле (2). Отметим, что стадии к2 и к3 в формуле (2) вычисляются в потенциально опасных точках tn + 0,5h и tn + h. Поэтому рассмотрим событийную функцию вида gn+1 = g(yn + hn +1 fn, tn + hn +1), т. е. на решении, полученном с использованием явного метода Эйлера. Разлагая gn+1 в ряд Тейлора и учитывая линейность функции g(y, t), имеем gn+1 = gn + hn+1 д^ fn + dsn) , (6)
+ dy dt )
где gn = g(yn , tn ),
∂g n ∂y
9g ( y n , t n ) dg n = dg ( y n , t n )
∂y , ∂t ∂t
В результате получаем зависимость gn+1 от прогнозируемого шага hn+1 Теорема [5]. Выбор шага по формуле hn+1 = (Y - Dgn! (dy fn + dt1) , (7)
где y G [0 , 1) , обеспечивает поведение событийной динамики как устойчивой линейной системы, которая приближается к поверхности g ( y, t ) = 0 • Кроме того, если g ( y о , t о ) < 0, то
g ( У п , t n ) < 0 для всех n .
Доказательство. Подставляя (7) в (6), имеем
9 n +i = Yg n
Преобразовав рекуррентно данное соотношение, получим g n +1 = Y n +1 g 0 . Так как Y < 1, то g n ^ 0 при n ^ то. Кроме того, из соотношения Y > 0 следует, что функция g n не меняет знак. Следовательно, при g 0 < 0 будет выполняться неравенство g n < 0 для всех n . Тогда событийная функция никогда не пересечет потенциально опасную область g ( y n , t n ) = 0. Теорема доказана.
Сформулируем алгоритм интегрирования с учетом прогноза шага через событийную функцию. Пусть решение y n в точке t n вычислено с шагом h n . Кроме того, известны значения стадий k 1 , k 2 и k 3 метода (2). Тогда можно выполнить следующий шаг:
Шаг 1. Вычисляется f n = f ( y n , t n ).
Шаг 2. Вычисляются gn = g(yn, tn), dgn/dy = dg(yn, tn)/dy, dgn/dt = dg(yn, tn)/dt.
Шаг 3. Вычисляется шаг h p n +1 по формуле (7).
Шаг 4. Вычисляется новый шаг hn+1 по формуле hn+i = min(hn+i, hnr+oi), pro где hn+1 задается соотношением hno = max[hn, min(hac, hst)].
Шаг 5. Выполняется следующий шаг интегрирования.
-
3. Результаты расчетов. С целью тестирования работы алгоритма рассмотрена типичная гибридная система двух осциллирующих масс на пружинах [11]. Система может находиться в одном из двух локальных состояний: “Раздельно” или “Вместе”. Поведение системы в каждом из состояний описывается системой дифференциально-алгебраических уравнений.
При s < Ik 1 n 1 — k2n2 — x 1(k 1 — k2)| имеем x1 = v 1, v 1 = k1(n 1 — x 1)/m 1, a 1 = k 1(n 1 — x 1)/m 1, x2 = v2, v*2 = k2(n2 — x2)/m2, a2 = k2(n2 — x2)/m2, (8)
при x 1 = x 2 и v 1 > v 2
a 1 = [ k 1 n 1 + k 2 n 2 — x i( k 1 + k 2)] /(m 1 + m 2), v 1 = [ k 1 n 1 + k 2 n 2 — x 1( k 1 + k 2)] /(m 1 + m 2), xL = v1, (9)
a 2 = [ k 1 n 1 + k 2 n 2 — x 1( k 1 + k 2)] /(m 1 + m 2), v 02 = [ k 1 n 1 + k 2 n 2 — x 1( k 1 + k 2)] /(m 1 + m 2), x02 = v2 , s = —s, где m1 и m2 — массы грузов; k1 и k2 — жесткости пружин; n1 и n2 — нейтральные координаты грузов; x1 и x2 — координаты грузов; v1 и v2 — скорости грузов; a1 и a2 — ускорения грузов; s — общая жесткость пружин в состоянии “Вместе”.
Ниже приведен текст компьютерной модели гибридной системы двух осциллирующих масс на языке LISMA [12].
k1=1; k2=2;
n1=1; n2=2;
m1=1; m2=1;
x1=0;
x2=3;
separate [s x1'=v1; v1'=k1*(n1-x1)/m1; a1 ~=k1*(n1-x1)/m1; x2'=v2; v2'=k2*(n2-x2)/m2; a2~=k2*(n2-x2)/m2; from; together [(x1>=x2) and (v1>=v2)] is s=10; v1=(m1*v1+m2*v2)/(m1+m2); v2=v1; v1' =(k1*n1+k2*n2-x1*(k1+k2))/(m1+m2); a1 ~ =(k1*n1+k2*n2-x1*(k1+k2))/(m1+m2); x1'=v1; v2' =(k1*n1+k2*n2-x2*(k1+k2))/(m1+m2); a2~ =(k1*n1+k2*n2-x2*(k1+k2))/(m1+m2); x2'=v2; s'=-s; from separate; Результаты анализа (8) и (9) в инструментальной среде ИСМА [9] с разработанным алгоритмом обнаружения (рис. 2,a) совпадают с результатами расчета эталонной модели в системе HyVisual [13]. Традиционный анализ системы без алгоритма обнаружения приводит к некачественным результатам (рис. 2,б). Рис. 2. Результаты компьютерного анализа гибридной системы двух масс, полученные с использованием алгоритма обнаружения (a) и без него (б) Заключение. Использование неравенства для контроля устойчивости фактически не приводит к увеличению вычислительных затрат, поскольку оценка максимального собственного числа матрицы Якоби системы (1) осуществляется через ранее вычисленные стадии и не приводит к росту числа вычислений функции f . Такая оценка получается грубой, однако применение контроля устойчивости в качестве ограничителя на рост шага позволяет избежать негативных последствий. Предложенный способ прогноза шага через событийную функцию распространяется на все явные методы типа метода Рунге – Кутты, поскольку при выборе шага используется только явный метод Эйлера.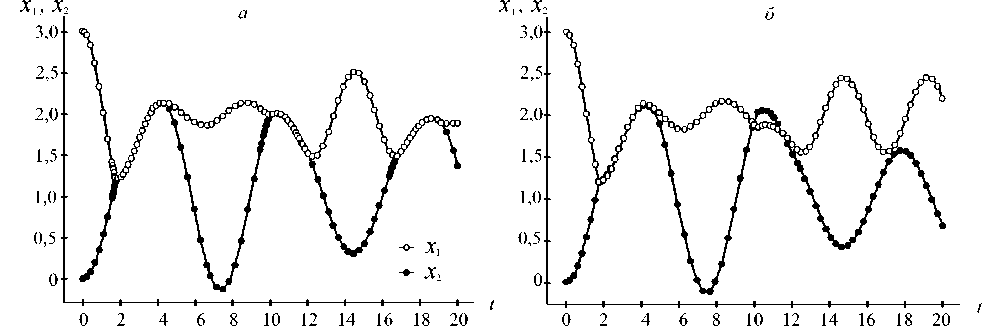
Список литературы Численное моделирование гибридных систем явным методом третьего порядка в инструментальной среде ИСМА
- Esposito J., Kumar V., Pappas G. J. Accurate event detection for simulating hybrid systems // Proc. of the 4th Intern. workshop "Hybrid systems: computation and control (HSCC 2001)", Rome (Italy), March 2001. Berlin: Springer-Verlag, 2001. V. 2034 P. 204-217. Новиков Е. А., Шорников Ю. В. Численное моделирование гибридных систем методом Рунге - Кутты второго порядка точности // Вычисл. технологии. 2008. Т. 13, № 2. С. 98-104. Новиков A. E., Новиков E. A., Шорников Ю. В. Моделирование гибридных систем явными методами // Вестн. КрасГАУ. Ресурсосберегающие технологии механизации сел. хоз-ва. 2009. № 5 С. 88-92. Хайрер Э. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи / Э. Хайрер, Г. Ваннер. М.: Мир, 1999. 685 c. Новиков Е. А., Шитов Ю. А., Шокин Ю. И. Одношаговые безытерационные методы решения жестких систем // Докл. СССР. 1988. Т. 301, № 6. С. 1310-1314. Новиков Е. А., Шитов Ю. А., Шокин Ю. И. О классе (m,k)-методов решения жестких систем // Журн. вычисл. математики и мат. физики. 1989. Т. 29, № 2. С. 194-201. Новиков Е. А., Шитов Ю. А. Алгоритм интегрирования жестких систем на основе (m,k)-метода второго порядка точности с численным вычислением матрицы Якоби. Красноярск, 1988. (Препр. ВЦ СО АН СССР; № 20). Новиков Е. А. Явные методы для жестких систем. Новосибирск: Наука, 1997. 197 с. Свидетельство об офиц. регистрации программы для ЭВМ № 2005610126. Инструментальные средства машинного анализа / Ю. В. Шорников, В. С. Дружинин, Н. А. Макаров, К. В. Омельченко, И. Н. Томилов. М.: Роспатент, 2005. Шорников Ю. В., Новиков Е. А., Достовалов Д. Н. Анализ устойчивости явных методов Рунге - Кутты в инструментальной среде ИСМА // Пробл. информатики. 2009. № 3. С. 42-51. Шорников Ю. В. Моделирование сложных динамических и гибридных систем в ИСМА // Науч. вестн. НГТУ. 2007. № 1. С. 79-88. Свидетельство об офиц. регистрации программы для ЭВМ № 2007611024. Программа языкового процессора с языка LISMA (Language of ISMA) / Ю. В. Шорников, И. Н. Томилов. М.: Роспатент, 2007.
- Lee E. A., Zheng H. Operational semantics of hybrid systems//Proc. of the 8th Intern. workshop "Hybrid systems: computation and control (HSCC 2005)", Zurich (Switzerland), March 2005. Berlin: Springer-Verlag, 2005. V. 3414. P. 25-53.


