Численное моделирование и экспериментальные оценки характеристик выносливости элементов конструкций
Автор: Маньшин Ю. П., Маньшина Е. Ю.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Машиностроение и машиноведение
Статья в выпуске: 1 т.20, 2020 года.
Бесплатный доступ
Введение. В алгоритме прогнозирования ресурса элементов машин взаимодействуют модели внешнего воздействия, сопротивления разрушению и развития во времени того или иного вида повреждения этих элементов. Рассматриваются прикладные вопросы сопротивления элементов машин усталостному разрушению. Выполняется адаптация научных исследований и нормативных материалов по определению характеристик выносливости к специфике конструкций и материалов строительно-дорожных машин и сельхозтехники. Цель работы - с помощью анализа существующих методов разработать рекомендации по расчетному определению параметров выносливости конструктивных элементов сельхозмашин.Материалы и методы. Исходными данными послужили научные исследования механики разрушения машиностроительных материалов и конструкций, а также стандарты по методам определения характеристик выносливости. Необходимость апробации методов определения характеристик выносливости для использования в проектах строительно-дорожных машин и сельхозтехники вытекает из специфики их конструкций, условий работы и отраслевых сортаментов материалов...
Предел выносливости, усталостное разрушение, усталостная трещина, сварное соединение, расчетно-экспериментальные методы
Короткий адрес: https://sciup.org/142223724
IDR: 142223724 | УДК: 62-192(075.8) | DOI: 10.23947/1992-5980-2020-20-1-79-86
Текст научной статьи Численное моделирование и экспериментальные оценки характеристик выносливости элементов конструкций
УДК 62-192(075.8)

Машиностроение и машиноведение
Numerical modeling and experimental estimates of structural member fatigue characteristics
Yu. P. Man’shin, E. Yu. Man’shina
Don State Technical University (Rostov-on-Don, Russian Federation)
Introduction. In the algorithm for predicting the resource of machine parts, models of external actions, fracture resistance, and temporal development of a particular type of damage to these units interact. The applied issues of the resistance of machine parts to fatigue failure are considered. The scientific research and regulatory materials are adapted to determine the characteristics of endurance to the specifics of structures and materials of the construction-and-road machinery and agricultural machinery. The work objective is to use the analysis of existing methods to develop recommendations for the calculated determination of the endurance parameters of structural members of the agricultural machines.
Materials and Methods. The initial data were scientific studies on the fracture mechanics of the engineering materials and structures, as well as standards for endurance characterization methods. The need to test methods for determining fatigue characteristics to use them in the road construction machinery and agricultural machinery projects follows from the specifics of their designs, operation conditions and industry-specific range of materials. Based on the analysis of existing methods, it is required to develop recommendations for the calculation of the endurance parameters of structural parts of the agricultural machines. For this, the components of the load-bearing systems of the staged design were presented in the form of a set of plates of the corresponding thickness; and the concept of the critical radius of the stress raiser at the welding sites was also used. Numerical methods using mathematical models were applied. The calculation results were verified through comparing them to experimentally determined fatigue characteristics of the members of a combine harvester on a test bench.
Results. Radius critical values of the stress raisers for various types of welds are obtained. The tables of the calculated and experimental endurance limits of the combine bearing components are well correlated and can be used under designing.
Discussion and Conclusions. The theoretical foundations laid down in the study open up great opportunities for applications to the design of various machines. The considered fragment of adaptation of the theoretical approach to the agricultural engineering objects can be used in the design of load-bearing systems in the related fields of engineering.
Введение. В расчетном и экспериментально-расчетном методах прогнозирования долговечности силовых конструкций наземных мобильных машин массового производства (автомобили, тракторы, строительнодорожные, гидромелиоративные, сельскохозяйственные, военная техника и др.) рекомендуется в качестве основного критерия надежности принимать начало образования усталостной трещины длиной 0,2–0,5 мм в условиях многоциклового разрушения 1 . При этом исходной информацией о свойствах конструкции является характеристика кривой усталости. Рассмотрим возможность развития методов определения характеристик сопротивления усталости деталей машин 2 .
Элементы конструкции представляются состоящими из пластин и работающими на растяжение-сжатие. Концентрация напряжений вызывается резким изменением толщины пластин с определенным радиусом кривизны ρ в местах перехода, вплоть до резкого надреза. Концентрация напряжений, связанная с образованием сварного шва на рассматриваемых пластинах, считается предметом самостоятельных исследований и учитывается как результат.
Правильный выбор параметров сопротивления усталостному разрушению деталей машин и несущих систем является основой расчетов ресурсов и прогнозирования надежности [1]. Рассмотрим методику и результаты расчетного определения характеристик сопротивления усталости элементов (зон) несущей конструкции на основе модели, представленной на рис. 1.
-
1 Когаев В. П., Махутов Н. А., Гусенков А. П. Расчеты деталей машин и конструкций на прочность и долговечность : Справочник. М. : Машиностроение, 1985. 224 с.
-
2 МР 206–86. Расчеты и испытания на прочность. Методы определения характеристик сопротивления усталости деталей машин с учетом рассеяния : Методические рекомендации / Всесоюзный научно-исследовательский институт по стандартизации в машиностроении. М. : ВНИИНмаш, 1986. 50 с.
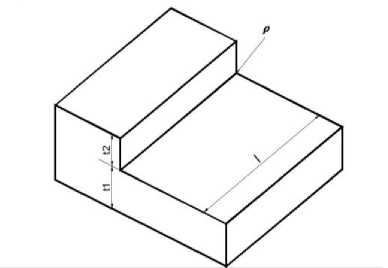
Рис. 1. Схема к расчетному определению характеристик сопротивления усталости
Модель представляет собой фрагмент сварного соединения из толстостенных элементов. Она типична для многих самоходных и прицепных машин наземного транспорта, например, рамно-каркасной системы самоходных комбайнов. Исходные данные для расчета приведены в табл. 1.
Таблица 1
Исходные данные для определения характеристик выносливости соединения деталей, представленных на рис. 1
|
Вариант |
1 |
2 |
3 |
4 |
|
Марка стали |
09Г2 |
09Г2 |
20 |
20 |
|
Условия работы |
коррозия |
коррозия |
||
|
ст b , МПа |
460 |
460 |
420 |
420 |
|
ст T , МПа |
300 |
300 |
250 |
250 |
|
ст ч , МПа |
232 |
232 |
213 |
213 |
|
V -1 |
0,069 |
0,069 |
0,062 |
0,062 |
|
K f ст |
0,85 |
0,55 |
0,85 |
0,58 |
|
KV |
0,50 |
0,50 |
0,50 |
0,50 |
|
K А |
0,95 |
0,95 |
0,95 |
0,95 |
|
t = t 2 , мм |
10 |
10 |
4 |
4 |
|
р , мм |
0,1–2 |
0,1–2 |
0,1–2 |
0,1–2 |
|
р , мм |
0,5 |
0,5 |
0,5 |
0,5 |
|
V P |
0,36 |
0,36 |
0,36 |
0,36 |
|
l , мм |
200 |
200 |
80 |
80 |
Медианное значение предела выносливости вычисляется по выражению 1, 2 :
ст
1 g где ст_1 — медианное значение предела выносливости, определяемого на гладких лабораторных образцах стан дартного диаметра d0 = 7,5 мм; K — коэффициент снижения предела выносливости:
K 1Л 1
--1---1,
Kdст Kfст J KvKa где K = ^-d — эффективный коэффициент концентрации напряжения; Kd — коэффициент влияния абсо- ст-1 g лютных размеров; KF ― коэффициент влияния состояния поверхности; KV ― коэффициент влияния поверх-
Машиностроение и машиноведение
1 Когаев В. П., Махутов Н. А., Гусенков А. П. Указ. соч. С 112–224.
2 ГОСТ 25.504–82. Расчеты и испытания на прочность. Методы расчета характеристик сопротивления усталости / Государственный комитет СССР по стандартам. Режим доступа : URL: (дата обращения : 11.12.2019).
ностного разупрочнения от металлургических процессов сварки; K ― коэффициент анизотропии свойств материала.
Для рассматриваемого примера воспользуемся рекомендациями [2]. Примем K V = 0,5, КА = 0,95 . Для нормальных условий эксплуатации примем KFa = 0,85 . При эксплуатации или хранении машины с попаданием пресной воды, влаги и образованием коррозии примем для стали 09Г2 по ГОСТ 5521-93 KFa = 0,55, для стали 20 по ГОСТ 2591-2006 KFa = 0,58 . Исходные данные для расчета выносливости образцов и их коэффициентов вариации V 1 приведены в табл. 1.
Для определения характерных отношений параметров методика 1 рекомендует формулу:
K а а а
Kdа 0,5Z, где а„ — теоретический коэффициент, определяющий степень возрастания напряжений в зоне их концентрации, рассчитывается по местному напряженно-деформированному состоянию с помощью конечно-элементных моделей; Z — параметр распределения.
Уравнение подобия усталостного разрушения близко по форме к распределению Вейбулла. Для пластинчатых элементов имеет вид 2 :
J = - 2,3lg(1 - p ) =
t + 1 2 ( u Y
( £-1Г •-------------------------------
G i I z J ( p + 1 )( p + 2 ) Z 2
,
где G 1 ― градиент первого главного напряжения, определяется по формуле: в
G i = 23/ p ; I u I = 0,0152 ( p + 1 ) ,
V z )
здесь V ― чувствительность металла к концентрации напряжений:
V a= 0,2 - 0,0001 а ь ;
р = — - 0,64.
V a
Медианное значение параметра Z получим при вероятности разрушения P = 0,5 из решения уравне- ния подобия (1). Для рассматриваемых деталей значения Z приведены в табл. 2.
Расчетные параметры сопротивления усталости конструкции (рис. 1)
Таблица 2
|
Вариант |
1 |
2 |
3 |
4 |
|
p кр , мм |
0,5 |
0,5 |
0,5 |
0,5 |
|
« а |
2,2 |
2,2 |
1,7 |
1,7 |
|
V aa |
0,19 |
0,19 |
0,22 |
0,22 |
|
Z |
2,12 |
2,12 |
2,51 |
2,51 |
|
V o |
0,154 |
0,154 |
0,158 |
0,158 |
|
в |
5,85 |
5,58 |
5,69 |
5,69 |
|
G 1 , 1/мм |
4,6 |
4,6 |
4,6 |
4,6 |
|
K а / K d а |
2,07 |
2,07 |
1,35 |
1,35 |
|
K |
4,74 |
6,09 |
3,22 |
4,57 |
|
0 |
0,49 |
0,49 |
0,20 |
0,20 |
|
V а max |
0,05 |
0,05 |
0,06 |
0,06 |
|
V а- 1 g |
0,21 |
0,21 |
0,24 |
0,24 |
|
^ Kth , МПа |
9,53 |
9,53 |
9,53 |
9,53 |
1 МР 206–86. Указ. норм. док. 1986. 50 с.
2 МР 206–86. Указ. норм. док. 1986. 50 с.
Средний градиент напряжений в зоне радиуса р , которая является местом концентрации, определен для условия:
Р = ( р кр ) » 0,5 - 0,0004 ( а 6 - 500 ) .
Для рассматриваемых сталей установлено критическое значение радиуса кривизны в соединении деталей
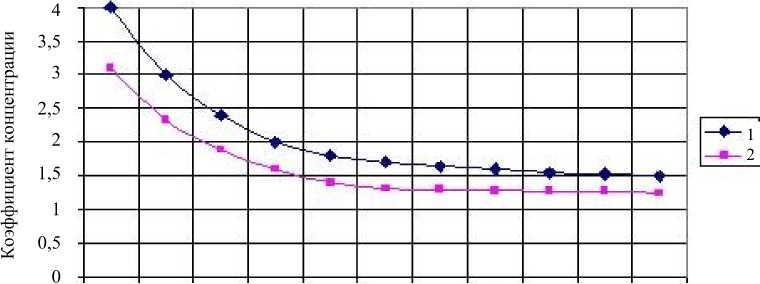
Рк? = 0,5 мм. Ему соответствует образование не распространяющихся в дальнейшем трещин усталости 1. По данному критерию проведен выбор величины aG. На рис. 2 представлены зависимости теоретического коэф- фициента концентрации напряжений от радиуса кривизны для различных геометрических параметров кон- струкции. Вычисленные медианные значения пределов выносливости для рассматриваемых деталей представлены в табл. 3.
0,1 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2
Радиус кривизны, мм
Рис. 2. Зависимости теоретического коэффициента концентрации напряжений от радиуса кривизны:
1 — t i = 1 2 = 10 мм; 2 — t i = 1 2 = 4 мм
Расчетные характеристики сопротивления усталости деталей, представленных на рис. 1
по исходным данным табл. 1
Таблица 3
|
Вариант |
1 |
2 |
3 |
4 |
|
a- 1 g |
49 |
38 |
66 |
46 |
|
( a- 1 g ) P = 0,05, МПа |
32 |
25 |
40 |
28 |
|
( a- 1 g ) P = 0,95, МПа |
66 |
51 |
92 |
64 |
|
m |
4,54 |
3,52 |
6,36 |
4,48 |
|
N ,106 циклов |
2,9 |
2,6 |
2,9 |
2,7 |
|
ya |
0,11 |
0,11 |
0,10 |
0,10 |
|
a- 1 gkp , МПа |
34 |
- |
- |
- |
Коэффициент вариации предела выносливости определен по выражению:
V a-i g = v V L+ V>V r, (2)
где V max ― коэффициент вариации максимальных напряжений в зоне концентрации; V 1 ― коэффициент вариации предела выносливости образца; V ― коэффициент вариации теоретического коэффициента в зоне концентрации.
Коэффициент вариации V 1 задан 2 и представлен в табл. 1 в виде исходных данных. Коэффициент вариации V max определяется по выражению 3 :
Машиностроение и машиноведение
-
1 Когаев В. П., Махутов Н. А., Гусенков А. П. Указ. соч. С. 112–224.
-
2 Когаев В. П., Махутов Н. А., Гусенков А. П. Указ. соч. С. 112–224.
-
3 МР 206–86. Указ. норм. док. 1986. 50 с.
V
a max
0,1
1 + 9 v a ,
где 9 — относительный критерий подобия усталостного разрушения:
.
88,3 G 1
Расчетные величины параметров приведены в табл. 2. Коэффициент вариации V определяется по рекоменда-циям 1 :
V aa
daa др
■ — V .
- а р р=р a
Для нахождения модуля производной осуществляется линейная аппроксимация функции aa = ф ( р / 1 ) , которая представлена на рис. 2 в окрестностях среднего значения параметра р . Результаты вычисления приведены в табл. 2. Там же содержатся результаты вычисления коэффициента вариации предела выносливости по выражению (2).
Определим значения предела выносливости в предположении его нормального распределения с вероятностью разрушения 5 % и 95 % по формуле:
( a -1 g ) P = a -1 g (1 + ZPVa-1 g ),
где Z P ― квантиль нормального распределения. В табл. 3 приведены значения предела выносливости с указан-
ными вероятностями разрушения.
Далее приведем зависимости для расчета параметров кривой усталости:
• показатель наклона левой ветви кривой усталости2:
m = 5 + — / K ;
I 80 J a
-
• абсцисса точки кривой усталости:
N = 1q 5 — (0.997-0.003 m ) ;
-
• коэффициент чувствительности к асимметрии цикла3:
Фс = 0.02 + 2 ■ 10 - 4 a b .
Результаты расчета этих характеристик для рассматриваемых деталей приведены в табл. 3.
Исследованиями установлено 4 , что в зонах концентрации напряжений существуют критические радиу
сы кривизны в диапазоне значений р кр = 0.1-0.6 мм [1]. При р < р кр имеют место другие закономерности подо
бия усталостного разрушения по сравнению с областью р > ркр . В этом случае рассматривается трещиноподобный предельно острый надрез, характерный для зон сварных швов соединяемых деталей в различных отраслях машиностроения [3, 4]. Рекомендуется 5 определить два предела выносливости:
1. Предел выносливости a _1 g при р > р . Он определяется по критериям появления первых микро-
скопических трещин усталости и зависит от радиуса кривизны.
2. Предел выносливости окончательного разрушения a_, при р < ркр . Он не зависит от радиуса кри-
визны надреза и определяется по формуле:
a , - 1 др
11,5 A K th
V t + р кр ’
где A Kth — порог развития усталостных трещин; t — глубина ступеньки в зоне концентратора напряжения.
Порог развития усталостных трещин для малоуглеродистых сталей с учетом коэффициента асимметрии ориентировочно можно определить по формуле 6 :
1 МР 206–86. Указ. норм. док. 1986. 50 с.
-
2 МР 206–86. Указ. норм. док. 1986. 50 с.
-
3 Когаев В. П., Махутов Н. А., Гусенков А. П. Указ. соч. С. 112–224.
-
4 Когаев В. П., Махутов Н. А., Гусенков А. П. Указ. соч. С. 112–224.
-
5 МР 206–86. Указ. норм. док. 1986. 50 с.
-
6 МР 206–86. Указ. норм. док. 1986. 50 с.
-
∆ Kth ≈ 6,74 1 - R . (3)
Параметр ∆ K th для рассматриваемых деталей указан в табл. 2 при R = 1 . Вычисленные по выражению (3) значения σ 1 g приведены в табл. 3.
Для оценки правомерности расчета усталости элементов конструкций, представленных в виде пластин с различными радиусами перехода в зонах соединения вплоть до предельно острого надреза, проведены стендовые испытания натурных образцов. Результаты испытаний представлены в табл. 4.
Экспериментальные характеристики сопротивления усталости металлоконструкций зерноуборочных машин
Таблица 4
|
Зона сварки |
m |
( σ -1 g ), МПа |
( σ -1 g ) P = 0,05 МПа |
( σ -1 g ) P = 0,95 МПа |
V V σ-1 g |
N ⋅ 106 циклов |
||||||
|
min |
сред нее |
max |
min |
среднее |
max |
по среднему |
по min |
по среднему |
по max |
|||
|
Фланца и корпуса моста ведущих колес |
3,2 |
3,7 |
4,3 |
31 |
37 |
43 |
4 |
4 |
70 |
81 |
0,54 |
3,7 |
|
Кронштейна КПП и корпуса ведущих колес |
3,1 |
3,9 |
4,7 |
31 |
39 |
47 |
24 |
19 |
54 |
65 |
0,23 |
3,6 |
|
Опорной плиты и корпуса моста ведущих колес |
3,5 |
4,1 |
4,8 |
33 |
38 |
43 |
21 |
18 |
55 |
62 |
0,27 |
3,9 |
|
Стойки каркаса |
4,2 |
4,9 |
5,6 |
38 |
45 |
52 |
35 |
29 |
55 |
64 |
0,14 |
4,1 |
Для проведении стендовых испытаний выбрана самая высокая группа точности при относительной погрешности 0,1 ≤ε≤ 0,2 , доверительная вероятность β= 0,8 . Число испытуемых конструкций находилось в диапазоне 11–14 ед.
Данные табл. 4 показывают большие разбросы эмпирических оценок. Даже если исключить из рассмотрения зону сварки фланца и балки моста ведущих колес, разброс значений для которой вызван нестабильностью технологического процесса, в заданном доверительном интервале величина σ 1 g отличается в 1,8– 2,9 раз.
Машиностроение и машиноведение
Выводы . Сравнение расчетных (табл. 3) и экспериментальных (табл. 4) характеристик сопротивления усталости в зонах сварных соединений показывает их хорошую сопоставимость. Интервалы доверительной вероятности экспериментальных значений перекрывают аналогичные интервалы расчетных значений для зон моста ведущих колес. Средние значения для условий нормальной работы отличаются в 1,3 раза, а при коррозии совпадают. Для металлоконструкций каркаса расчетные значения по нормальным условиям отличаются в 1,5 раза, а по условиям коррозии практически совпадают. Хорошее соответствие реальным значениям показывают величины σ 1 g , вычисленные по порогу развития усталостных трещин.
Представленные материалы позволяют сделать вывод о достаточной достоверности на этапе прогнозирования долговечности использования расчетных характеристик сопротивления усталости по предлагаемой методике. Корректные характеристики сопротивления усталости при известном или полученном из полевого эксперимента распределении могут служить фундаментом для расчета ресурса конструкции с требуемой вероятностью безотказной работы, вытекающей из технического задании для соответствующей машины [5].
Таким образом, путем анализа существующих методов разработаны рекомендации по расчетному определению параметров выносливости конструктивных элементов сельхозмашин. При доработке проекта или опытного образца изделия до нормативной долговечности с помощью конструктивных и технологических при-
ёмов характеристики сопротивления усталости используются в методах приближенных и функциональных оценок ресурса [6, 7].
Список литературы Численное моделирование и экспериментальные оценки характеристик выносливости элементов конструкций
- Спиченков, В. В. Современные методы расчетной оценки силовых конструкций / В. В. Спиченков, А. Б. Шостенко; Ростовский институт автоматизации и технологии машиностроения // Разработка конструкций и исследование технологических процессов сельскохозяйственных машин: сб. статей. - Ростов-на-Дону, 1993. - С. 69-75.
- Кeшe, Г. Коррозия металлов. Физико-химические принципы и актуальные проблемы / Г. Кeшe. - Москва: Металлургия, 1984. - 400 с.
- Ефремов, Л. В. Практика инженерного анализа надежности судовой техники / Л. В. Ефремов. - Ленинград: Судостроение, 1980. - 175 с.
- Лукинский, В. С. Прогнозирование надежности автомобилей / В. С. Лукинский, Е. И. Зайцев. - Ленинград: Политехника, 1991. - 222 с.
- Маньшин, Ю. П. Вопросы надежности деталей при проектировании механических систем / Ю. П. Маньшин, Е. Ю. Маньшина // Вестник Московского государственного технического университета им. Н. Э. Баумана. Сер. Машиностроение. - 2019. - № 5. - С. 56-73.
- Маньшин, Ю. П. Приближенная оценка ресурса детали, обеспечивающая ее требуемый ресурс с заданной вероятностью безотказной работы / Ю. П. Маньшин, Е. Ю. Маньшина // Вестник машиностроения. - 2017. - № 12. - С. 20-24.
- Man'shin Yu.P. Estimating the Life of a Machine Part / Yu.P. Man'shin, E. Yu. Man'shina// Russian Engineering Research. - 2018. - Vol. 38, no. 3. - P. 157-162.


