Численное моделирование эксперимента по импульсному воздействию на пьезоэлектрический генератор стекового типа

Введение. В последние годы получили развитие исследования, посвященные разработке пьезоэлектрических преобразователей механической энергии колебаний объектов в электрическую. Наиболее известны пьезоэлектрические преобразователи энергии двух конфигураций: осевого (стекового) и кантилеверного типа, которые имеют неограниченный срок эксплуатации, если внешние механические и температурные воздействия не приводят к необратимому уменьшению поляризации их активных элементов или их разрушению [1 –3]. Большинство из этих работ посвя-

Механика

щены изучению характеристик пьезоэлектрических генераторов (ПЭГ) кантилеверного типа («мода колебаний d 31 »). ПЭГ осевого типа исследованы в меньшей степени. В частности, известны работы, в которых приведены результаты теоретических исследований характеристик ПЭГ, работающих на «продольной моде d 33 колебаний» [3, 4]. Работы [4– 7] посвящены построению моделей ПЭГ на основе колебаний механической системы с сосредоточенными параметрами. Использование таких систем является удобным модельным подходом, так как позволяет получить аналитические зависимости между выходными параметрами ПЭГ (потенциалом, мощностью и т.п.) и электрическими, механическими характеристиками и сопротивлением внешней электрической цепи, однако, как показано в [8] диапазон их применения весьма ограничен. Более полные результаты исследований многослойных ПЭГ осевого типа приведены также в других работах [10, 11]. В них описаны результаты исследований характеристик ПЭГ, как осевого, так и кантилевер-ного типов. В [10] приведены интересные результаты температурных зависимостей параметров ПЭГ с чувствительным элементом (ЧЭ) из сегнетомягкой пьезокерамики ПКР–46. К сожалению, константы этого состава пьезокерамики не приведены, а это не позволяет провести сравнительный анализ достоверности измеренных параметров ПЭГ с известными, описанными, например, в [9]. В обзоре [11], опубликованном позднее, описаны области применения маломощных ПЭГ в основном кантилеверного типа с присоединенной массой. Также приведены только общие данные о разработанных за рубежом ПЭГ осевого типа, в которых используется механическая энергия при движении человека, т.е. в режиме циклических нагрузок. Более подробных данных о результатах исследований таких ПЭГ, к сожалению, не приведено. Выбор импульсного режима нагружения обусловлен областью применения ПЭГ осевого типа в качестве перспективных автономных источников энергии, преобразующих механическую энергию периодических воздействий из внешней среды, в том числе не гармонических, в электрическую. В частности, эти ПЭГ могут быть использованы для преобразования механической энергии колебаний рельсов железнодорожного транспорта или дорожного полотна автодороги в электрическую энергию.

Приведенный выше краткий анализ известных работ показал, что задача создания ПЭГ осевого типа большой мощности с эффективными выходными параметрами при действии импульсных нагрузок в полном объеме пока не решена, хотя и достаточно актуальна. Авторами получены экспериментальные и численные результаты исследований временных зависимостей выходных характеристик многослойного пьезоэлектрического генератора осевого типа от величины импульсных механических сжимающих напряжений при различных значениях электрического сопротивления нагрузки.

Объект исследования и методика эксперимента . Приведем результаты исследований характеристик одной модели многослойного ПЭГ стекового типа. Его ЧЭ состоит из 11 параллельно соединенных пьезоэлементов (ПЭ) дискового типа каждый толщиной 1 мм с внешним и внутренним диаметром 18 и 8 мм, соответственно. Общая высота ЧЭ составляет 11,3 мм, а общая электрическая емкость 20,22 нФ. При этом каждый из ПЭ поляризован по толщине, в качестве материала ЧЭ была использована пьезокерамика ЦТС-19, материальные константы которой приведены в таблице 1.

Таблица 1

	Материальные константы пьезокерамики ЦТС-19:
E C 11 , ГПа	C 1 E 2 ,          C 1 E 3 ,          C 3 E 3 ,          C 4 E 4 ,           e 31 ,           e 33 ,           e 15 ,         ε 11 / ε 0       ε 33 / ε 0 ГПа     ГПа     ГПа     ГПа     Кл/м 2      Кл/м 2     Кл/м 2       -        -
109	61        54        93        24       -4.9       14.9       10.6      820      840

Испытание ПЭГ производились на лабораторной установке импульсного нагружения ПЭГ, работающих на продольных колебаниях. Структурная схема установки представлена на рис. 1.

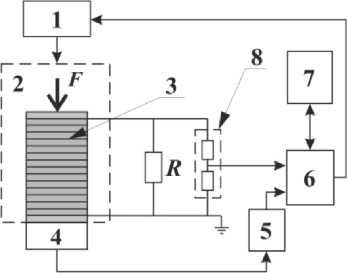
Рис. 1. Структурная схема испытательного стенда. 1 — частотный преобразователь; 2 — нагружающий модуль;

3 — испытуемый образец многослойного пьезопреобразователя (ПЭГ осевого типа); 4 — тензометрический динамометр;

5 — тензоусилитель; 6 — АЦП/ЦАП; 7 — персональный компьютер с установленным ПО PowerGraph;

8 — делитель напряжения; R — сопротивление электрической нагрузки

На рис. 2 приведена фотография нагружающего модуля испытательной установки, размещенной на общем основании, справа вверху — фотография ЧЭ (аппаратная часть стенда не показана).

Рис. 2. Фотография лабораторной силовой части испытательной установки для определения характеристик ПЭГ осевого типа.

1 — частотный преобразователь, задающий частоту вращения двигателя от 10 до 1400 об/мин; 2 — двигатель с редуктором и эксцентриковым диском, и шатуном; 3 — механический рычажный усилитель изменения сжимающего усилия с коэффициентом преобразования 50; 4 — испытуемый образец ПЭГ; 5 — тензометрический динамометр; 6 — опорный кронштейн

Образец подвергался механическому циклическому нагружению при сжимающей импульсной силе с амплитудой от 1 кН и до 4 кН. Для каждого цикла сжимающего усилия, измеряемого с помощью динамометра, регистрировались временные зависимости величины сжимающей силы и выходного напряжения пьезогенератора при различных дискретных значениях нагрузочного сопротивления R от 10 кОм до 22 мОм. Регистрация временных зависимостей характеристик ПЭГ проводилась с учетом влияния сопротивления нагрузки на форму импульсов выходного напряжения ПЭГ. Такое влияние характеризуется «степенью неискаженности передачи электрического сигнала», а в нашем случае пьезоэлектрического отклика ЧЭ. Как известно [12], режим неискаженной передачи электрического импульса на регистратор сигнала определяется соотношением

RC ≥ τ , где τ — длительность импульса сжимающего усилия; R — сопротивление электрической нагрузки; C — электрическая емкость активного элемента ПЭГ.

Результаты экспериментальных измерений. По результатам экспериментальных измерений получены сопряженные временные зависимости силового механического воздействия и выходного электрического напряжения испытуемой модели ПЭГ от величины механического усилия и электрического нагрузочного сопротивления R .

Механика

На рис. 3 показаны сопряженные временные зависимости воздействующего сжимающего механического импульса силой амплитудой до 3,1 кН (кривая 4) и соответствующих пьезоэлектрических откликов на выходе ПЭГ при различных значениях сопротивлениях нагрузки R : 0,374; 2,572 и 22,77 МОм (кривые 1, 2 и 3).

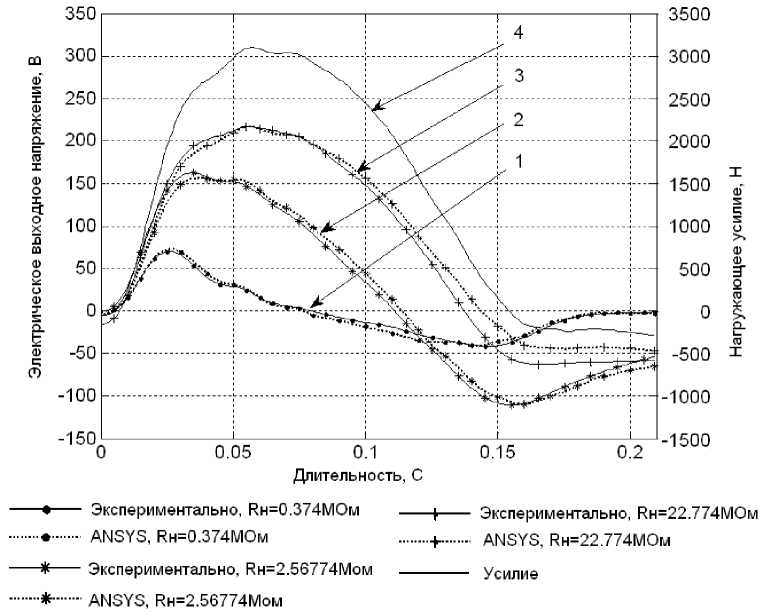
Рис. 3. Временные зависимости воздействующего сжимающего механического импульса величиной силы амплитудой до 3,1 кН (кривая 4) и соответствующих пьезоэлектрических откликов на выходе ПЭГ при различных значениях сопротивлениях нагрузки R : 0,374; 2,572 и 22,77 МОм (кривые 1, 2 и 3) соответственно, полученные из физического эксперимента (сплошные линии) и численного конечно-элементного расчета (пунктирные линии)

Сравнение форм сигналов пьезоэлектрического отклика при различных значениях R (кривые 1, 2, 3) и импульса усилия сжатия (кривая 4) показало, что с ростом R формы выходного напряжения стремятся к форме возбуж- дающего импульса механического напряжения.

Конечно-элементное моделирование. В ANSYS была построена осесимметричная конечно-элементная мо дель ПЭГ (рис. 4), адекватная физической модели, рассмотренной выше.

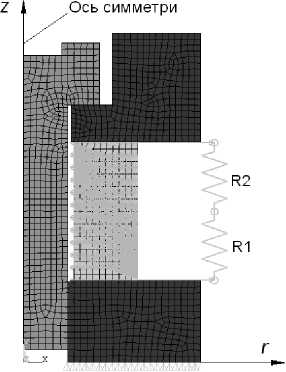
Рис. 4. Осесимметричная конечно-элементная модель ПЭГ с активной нагрузкой

На первом этапе было проведено численное исследование по выбору шага интегрирования по времени уравнений МКЭ по схеме Ньюмарка для нестационарной задачи, в результате которого он был выбран равным 0,2 мкс. При этом результаты зависимости выходного напряжения от времени близки к результатам физического эксперимента (рис. 3, кривые 1-3).

Далее была решена статическая задача для случая сжимающего усилия, воздействующего на ЧЭ ПЭГ равного 3,1 кН, в результате которого было получено значение выходного напряжения V0, равное 722 В. Проведенная серия нестационарных расчетов для различных значений величины R активной нагрузки при импульсном нагружении показала, что при возрастании R выходное напряжение стремится к форме напряжения для разомкнутой цепи, максимальное значение которого совпадает с V0.

Далее были проведены расчеты в ANSYS , по результатам которых были получены зависимости выходного напряжения от времени с изменением сжимающей нагрузки на участке от 0 до 0,21 с. при R равном 0,374; 2,572 и 22,77 МОм. Результаты этих расчетов отражены на графике временной зависимости выходного напряжения, полученной из физического эксперимента (рис. 3). Сравнение результатов расчетов и эксперимента в этих случаях показывает достаточно хорошее их совпадение. Так как скорость нагружения ЧЭ ПЭГ достаточно мала по сравнению со скоростью упругих волновых процессов, то численное решение задачи соответствуют квазистатической постановке.

Следующий этап численного исследования связан с анализом частотной зависимости выходного напряжения ПЭГ при гармоническом возбуждении колебаний силой с амплитудой 3 кН. Эти расчеты показали, что при величине активного сопротивления 22 МОм и выше, значение выходного потенциала достигает некоторого предельного значения, начиная с частоты колебаний 0,2 Гц, в широком частотном диапазоне до первого резонанса.

Однако это не означает, что при этих значениях частоты и сопротивлении нагрузки можно на выходе достигнуть максимума выходной мощности ПЭГ. Авторами ранее было доказано, что зависимости выходного напряжения и выходной мощности от скорости механического нагружения существенно отличаются, во всяком случае в диапазоне скоростей до 4,1 кН/с [13]. Поэтому для более детального анализа этой особенности возникла необходимость расчета выходных характеристик ПЭГ в достаточно широком диапазоне скоростей нагружения. Ниже приведены результаты такого расчета с помощью аппроксимации нагрузки рядом Фурье на основе упрощённой электромеханической модели многослойного ПЭГ [14].

Предполагается, что генератор возбуждается осевым сжимающим нагружением p(t) на частотах, гораздо меньших собственной резонансной частоты, что в свою очередь позволяет описать динамику системы с электромеханической связью уравнением первого порядка. Если к ПЭГ, состоящему из N слоев, поляризованных по толщине, параллельно подключено сопротивление нагрузки R , то определяющее уравнение, описывающие систему выглядит следующим образом

N d

Е- f- DndA i i = 1 dt ( Ai

v ⁽ t ) R ’

где v(t) — напряжение на резисторе; D — вектор электрического смещения; n — вектор нормали поверхности электрода; A i — площадь поверхности электрода i- го слоя. Представим вектор электрического смещения в виде:

D i = d ijk T ij _+Б Tj E j .                                                     (2)

Подставив (2) в (1), получим уравнение (3), описывающее динамику системы:

C peq V ( t ) + 1 v ( t ) = d ef Ap ( t ),                                                (3)

R

Cp = Me T3 A / h, d3ff = Nd33 , где Cp — эквивалентная емкость; h — толщина одного слоя ПЭГ; def — эффективный пьезомодуль; X и ц — эмпи- рические константы, введённые в силу различия между моноблочной и многослойной конфигурациями ПЭГ, а также эффектов, накладываемых технологией производства многослойных ПГ.

В случае, если нагружение обладает произвольной формой, как например, на рис. 3, то амплитудные значения механической нагрузки p(t) можно представить набором дискретных значений, а затем интерполировать с помощью рядов Фурье:

N

Р(t) = m о ' Е k=1

(. 2nt A         f , 2nt m cosl k 1 + n sml k k       Tk T

где m₀ — среднее значение; О — длительность нагружения; m k , n k — коэффициенты Фурье:

1 гT z x ,             2 _o         f, 2nt A ,            2 T _x f, 2nt A ,

^m о = T I ° P ⁽ t ) ^{dt ,    m} k = T f o P ⁽ t ^)cos l ^kT I ^{dt ,   n} k = T f o P ⁽ t ^)sin l k T I ^dt .

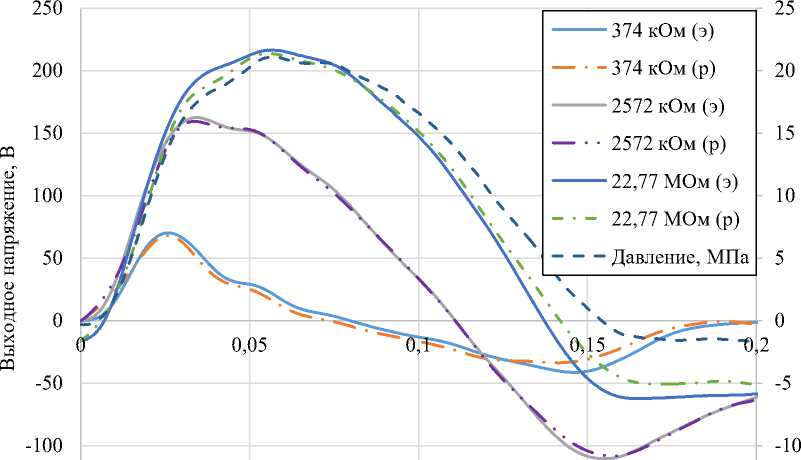
Затем полученное приближение (4) можно подставить в уравнение (3) и решить численно, например, методом Рунге-Кутта. Результаты численного моделирования с использованием одномерной модели, приведённые на рис. 5, показали высокую сходимость с результатами КЭ расчета, приведённого на рис. 3, во всяком случае в диапазоне низких частот колебаний ПЭГ стековой конфигурации. Однако, объем вычислений в последнем случае меньше, чем при

Механика

конечно-элементном моделировании. При расчете зависимости выходного напряжения ПЭГ при частоте импульсного воздействия ниже 0,2 Гц и сопротивлении нагрузки до 22 МОм можно получить выходное напряжение не более 100 В. Однако, расчет выходной мощности ПЭГ при указанной выше скорости механического нагружения составляет всего 0.05 мВт в случае сопротивления нагрузке 22 МОм, а при сопротивлении 0.374 МОм можно достичь существенно большей выходной мощности, равно при прочих равных условиях 8 мВт.

-150                                                                               -15

Время, с

Рис. 5. Результаты численного расчета выходных характеристик ПЭГ с помощью аппроксимации механической нагрузки рядом Фурье: (э) — эксперимент, (р) — расчёт

Выводы.

• 1.    Разработана методика и изготовлена лабораторная установка для проведения экспериментальных измерений параметров ПЭГ при их механическом импульсном нагружении.

• 2.    Разработана конечно-элементная модель устройства в ANSYS и проанализирована аналитическая упрощенная одномерная модель.

• 3.    Установлено, что временные зависимости воздействующего сжимающего механического импульса и соответствующих пьезоэлектрических откликов на выходе ПЭГ при различных значениях сопротивлениях нагрузки, полученные из физического эксперимента и численного, как конечно-элементного, так и аналитического расчета показывает достаточно хорошее их совпадение.

• 4.    Сравнение форм сигналов пьезоэлектрического отклика при увеличении R (кривые 1, 2, 3 на рис. 3) и импульсов усилия сжатия (кривая 4, рис. 3) показало, что с ростом R формы выходного напряжения стремятся к форме возбуждающего импульса механического напряжения.

• 5.    Показано, что режим неискаженной передачи пьезоэлектрического отклика ПЭГ стекового типа достигается при электрическом сопротивлении нагрузки выше 22 МОм для данного ПЭГ. Результаты КЭ расчета выходных характеристик ПЭГ исследованного типа подтвердили достоверность этого вывода.

• 6.    Установлено, что частотная зависимость выходного напряжения ПЭГ осевого типа имеет сложный характер, зависящий как от уровня сжимающей импульсной нагрузки и величины пьезомодуля d 33 материала чувствительного элемента ПЭГ, так и от электрического сопротивления нагрузки.