Численное моделирование мозгового кровотока методом крупных частиц

Проведено комплексное исследование, которое позволило численно

Передняя соединительная

Средняя мозговая

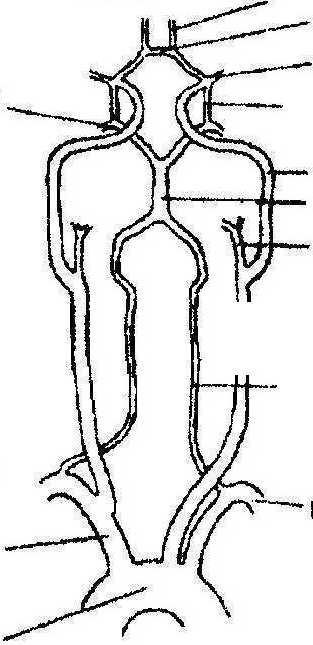
промоделировать течение крови в артериях головного мозга и, в частности, в окрестности области бифуркации сонной артерии человека [1-5]. Структура артерий головного мозга описана в ряде отечественных и зарубежных монографий [6-8 и др.]. На рис. 1 приведена схема сосудов, питающих головной мозг человека, взятая из [4]. На правой стороне этого рисунка видна общая сонная артерия (Common Carotid), разветвляющаяся в области бифуркации на внутреннюю сонную артерию (Internal Carotid) и внешнюю сонную артерию (External Carotid). В области бифуркации канал общей сонной артерии разделяется на два канала существенно разной толщины: диаметр внутренней сонной артерии значительно больше диаметра внешней сонной артерии. С гидродинамической точки зрения данная задача аналогична задаче о течении жидкости в окрестности точки разветвления трубопроводов (например, в жидкостной системе охлаждения атомных реакторов).

Передняя мозговая

Задняя мозговая

Плече-головной ствол (безымянная артерия)

Задняя соединительная

---Общая сонная

— Позвоночная

Подключичная

Внутренняя сонная

Основная

Наружная сонная

На рис. 2 изображён реальный вид этих артерий в окрестности области бифуркации (Б): общая сонная артерия (ОСА), внутренняя сонная артерии (ВнутрСА) и внешняя сонная артерия (ВнешСА).

Дуга аорты

Рис. 1. Схема сосудов, питающих головной

мозг человека

Рис. 2. Вид артерий в окрестности области бифуркации

Изучение кровотоков в сосудах головного мозга весьма актуально и представляет собой сложную задачу. В [4, 5] обсуждается постановочная часть численного эксперимента ио изучению гемодинамики в сосудах головного мозга с помощью метода крупных частиц - наиболее мощного современного метода вычислительного эксперимента. Этот метод был предложен в нашей стране одним из авторов настоящей статьи и стал в прямом смысле энциклопедическим: вошёл во все математические энциклопедии мира [9 - И и др.]. С помощью метода крупных частиц решены многие сложнейшие нелинейные задачи науки и техники [12 и др.].

С геометрической точки зрения постановка данной задачи о течении в окрестности точки бифуркации общей сонной артерии включает в себя следующую иерархию моделей:

• 1)    рассмотрение соединения вод надлежащими углами трёх жёстких круглых груб соответствующих калибров,

• 2)    рассмотрение соединения 'трёх гидроупругих труб,

• 3)    соединение каналов с усложнённой геометрией (например, с учётом конфигурации склеротической бляшки).

Любая сложная геометрия сосудов (в том числе с патологи веским и изменениями) может быть описана с помощью предложенной одним из авторов данной статьи методики дробных ячеек [13].

Численный эксперимент проводится методом крупных частиц [9 - 11]. Используется электрически нейтральная физическая модель (без учёта электрических зарядов частиц крови и стенок сосудов). Стенки сосудов предполагаются жёсткими с неизменной геометрией. Так как скорость течения крови в общей сонной артерии (^30 см/с) существенно дозвуковая, то при постановке краевых условий в начальном и выходном сечениях для обеспечения вычислительной устойчивости целесообразно использовать правый и левый инварианты Римана [14].

При реализации численного эксперимента необходимо свойства крови определить как с качественной, так и с количественной точек зрения. Нужно знать, к какому типу жидкостей принадлежит кровь, чтобы выбрать адекватную реологическую модель. Далее нужно получить количественные коэффициенты реологических констант (например, вязкости).

Рядом отечественных и зарубежных авторов [15 и др.] приводятся различные данные по механическим свойствам крови. При этом движение крови в крупных и средних сосудах считается этими авторами ламинарным. Молекулярная вязкость определяется эффектами обмена импульсом и энергией на микроуровне [16, 17]. В реальных течениях, в том числе при кровотоке в крупных и средних сосудах, обмен обычно существенно более интенсивен и определяется турбулентным переносом.

Существуют традиционные методы определения вязкости крови. Однако вязкость, определяемая в визкозимстрах, соответствует вязкости не собственно крови, текущей в кровеносных сосудах живого организма, а вязкости некоторой искусственно созданной дисперсной среды. Дело в том, что кровь, взятая для анализа, быстро свёртывается и её нельзя непосредственно ввести в визкозиметр. Первые нити фибрина в извлечённой из здорового организма крови появляются через 2 минуты, полное свёртывание крови заканчивается через 5 минут. Для сохранения крови в жидком состоянии в неё необходимо ввести антисвёртывающий препарат (например, гепарин). При этом в дальнейшем мы будем с необходимостью исследовать вязкость не чистой крови, а смеси крови с антисвёртывающим препаратом.

В результате проведённых авторами физических экспериментов были определены нелинейные характеристики вязкости крови и её плазмы в зависимости от концентрации введения в кровь гепарина. Некоторые результаты приведены ниже в таблицах (табл. 1 - табл. 3).

В табл. 1 вязкость определялась в ротационном визкозиметре при большой скорости сдвига (128 1/с). Это соответствует условиям течения крови в крупных сосудах.

В табл. 2 вязкость определялась в ротационном визкозиметре при умеренной скорости сдвига (28 1/с), что соответствует условиям течения крови в мелких сосудах.

В обоих случаях как для крупных (табл. 1), так и для мелких сосудов (табл. 2) мы наблюдаем чёткий максимум вязкости гидровзвеси «кровь - гепарин» при определённой концентрации гепарина. Отметим, что этот максимум отчётливо проявляется в крови всех доноров, сдавших свою кровь для исследования. Возраст доноров варьировался в широких пределах.

Исследование зависимости вязкости плазмы крови от концентрации вводимого гепарина дало качественно аналогичные результаты. Для плазмы максимум вязкости достигается при несколько большем значении концентрации гепарина (0,0077). В целом вязкость плазмы, как и следовало ожидать, в несколько раз меньше вязкости крови. Это происходит оттого, что в плазме отсутствуют форменные элементы крови.

Таблица 1

Зависимость вязкости крови от концентрации гепарина для большой скорости сдвига

Номер пробы крови	Объём взятой крови (мл)	Объём введённого гепарина (мл)	Вязкость крови и 102[П|-= ц ГСП]	Концентрация гепарина	Относительная вязкость крови
1	4	0,01	4,668	0,002494	0,9739203
	4	0,05	4,793	0,012346	1
	4	0,09	4,657	0,022005	0,971625287
	4	0,13	4,498	0,031477	0,938451909
2	4	0,01	4,94	0,002494	0,97320725
	4	0,05	5,076	0,012346
	4	0,09	4,953	0,022005	0,975768322
	4	0,13	4,849	0,031477	0,95 5279748
3	4	0,01	4,226	0,002494	0,973957133
	4	0,05	4,339	0,012346	1
	4	0,09	4,158	0,022005	0,958285319
	4	0,13	4,09	0,031477	0,942613 505
4	4	0,01	5,008	0,002494	0,96511852
	4	0,05	5,189	0,012346	1
	4	0,09	4,989	0,022005	0,961456928
	4	0,13	4,793	0,031477	0,923684718
5	.      4	0,01	6,424	0,002494	0,974218987
	4	0,05	6,594	0,012346	1
	4	0,09	6,401	0,022005	0,970730968
	4	0,13	6,278	0,031477	0,952077646
6	4	0,01	4,457	0,002494	0,969334493
	4	0,05	4,598	0,012346	1
	4	0,09	4,413	0,022005	0,959765115
	4	0,13	4,291	0,031477	0,93 323184

В табл. 3 для контроля приведены вязкости крови для новой группы доноров (для скорости сдвига 128 1/с) с иными, чем в табл. 1, концентрациями гепарина.

В табл.1 -табл. 3 приведены относительные вязкости крови, равные частному от деления вязкости исследуемого образца на максимальную вязкость крови данного донора при концентрации гепарина, равной, как отмечалось выше, 0,005.

При дальнейшем уменьшении концентрации гепарина (< 0,0025) вначале по-прежнему заметно снижение величины вязкости, хотя градиент уменьшается и в дальнейшем становится нулевым (при концентрации гепарина ~ 0,00215).

Экспериментально выявленная сложная нелинейная зависимость чётко соответствует физике процесса и логически непротиворечива. Из физических соображений следует, что в «нулевой точке отсчёта», где концентрация гепарина равна минимальному физиологическому уровню живого организма, вязкость крови будет больше, чем при введении дополнительного гепарина. Так как гепарин уменьшает вязкость, то при его введении вязкость жидкостной системы «кровь - гепарин» будет уменьшаться, что мы и наблюдаем при малых концентрациях гепарина. В некоторой точке будет достигнут минимум вязкости. При дальнейшем увеличении концентрации гепарина эффект разведения нивелируется биохимическими реакциями и наблюдается аномальное возрастание вязкости крови с увеличением доли гепарина в смеси. Далее вновь вязкость крови понижается по мере увеличения доли гепарина.

Таблица 2

Зависимость вязкости крови от концентрации гепарина для небольшой скорости сдвига

Номер пробы крови	Объём взятой крови (мл)	Объём введённого гепарина (мл)	Вязкость крови ц-1оТп] = = Р.ГСП1	Концентрация гепарина	Относительная вязкость крови
1	4	0,01	6,049	0,002494	0,9503 53496
	4	0,05	6,365	0,012346	1
	4	0,09	6,052	0,022005	0,950824823
	4	0,13	5,839	0,031477	0,917360566
2	4	0,01	6,838	0,002494	0,970204313
	4	0,05	7,048	0,012346	1
	4	0,09	6,891	0,022005	0,977724177
	4	0,13	6,68	0,031477	0,947786606
3	4	0,01	5,418	0,002494	0,990493601
	4	0,05	5,47	0,012346	1
	4	0,09	5,207	0,022005	0,951919561
	4	0,13	5,155	0,031477	0,942413163
4	4	0,61	6,996	0,002494	0,977231457
	4	0,05	7,159	0,012346	1
	4	0,09	6,962	0,022005	0,97248219
	4	0,13	6,728	0,031477	0,93 9796061
5	4	0,01	9,152	0,002494	0,966624419
	4	0,05	9,468	0,012346	1
	4	0,09	9,099	0,022005	0,961026616
	4	0,13	8,894	0,031477	0,939374736
6	4	6,01	6,672	0,002494	0,9793042 71
	4	0,05	6,813	0,012346	1
	4	0,09	6,529	0,022005	0,958314986
	4	0,13	6,397	0,031477	0,938940261

Таблица 3

Зависимость вязкости крови от концентрации гепарина для большой скорости сдвига и новой группы доноров

Номер пробы крови	Объём взятой крови (мл)	Объём введённого гепарина (мл)	Концентрация гепарина	Вязкость крови ц102[П] = - МСП]	Относительная вязкость крови
1	4	0,01	0,002494	4,361	0,990011
	4	0,02	0,004975	4,405	1
	4	0,03	0,007444	4,373	0,99273 6
	4	0,04	0,009901	4,299	0,975936
2	4	0,01	0,002494	4,426	0,974675
	4	0,02	0,004975	4,541	1
	4	0,03	0,007444	4,457	0,981502
	4	0.04	0,009901	4,396	0,968069

Важным экспериментальным средством исследования кровотока является ультразвуковая доплерография [18-20 и др.]. Она позволяет проводить сканирование крупных и средних кровеносных сосудов и определять скорости кровотока. При этом могут быть обнаружены особенности кровотока: зоны аномально турбулизированных областей за склеротическими бляшками и т.п. Эти данные могут служить тестами при численном моделировании . кровотока, На рис. 3 - 4 приведены результаты доплерографии, проведённые одним из авторов. На рис. 3 показан кровоток во внутренней сонной артерии (дан вариант кровотока при наличии в сосуде склеротических бляшек). Разным оттенкам на рисунках соответствуют разные величины скорости. Видно, что за бляшками реализуется зона с пониженными величинами модулей скоростей (тёмная область). На рис. 4 показано турбулентное течение в изгибе позвоночной артерии (резко меняющаяся от точки к точке гамма оттенков). .

Рис. 3. Кровоток во внутренней         Рис.4. Турбулентное течение в изгибе сонной артерии                       позвоночной артерии

В расчётах методом крупных частиц диаметр общей сонной артерии варьировался в пределах 10-12 мм, диаметр наружной сонной артерии - 5-7 мм, диаметр внутренней сонной артерии — 9-10 мм. .

Авторами были проведены многочисленные расчёты. Отмечена вихревая структура потока в окрестности места ветвления сосудов. В пристеночном слое преобладает плазма, в которой клетки крови - единичные эритроциты - ориентированы параллельно продольному сечению сосуда. Некоторыми авторами допускается формирование из нескольких эритроцитов так называемых "монетных, столбиков" (слипание эритроцитов) при движении в крупных сосудах. В этом случае данные дисперсные частицы с соответствующими линейными размерами будут' представлять ещё одну компоненту несомой среды.

Рассмотрим вначале ламинарный режим течения крови (рис. 5) на прямолинейном (неискривлённом) участке кровеносного сосуда радиусом R. В этом случае реализуется течение Пуазейля (рис. 5, рис. 6,а) с параболическим распределением скоростей по радиусу [16. 17]:

и(у) = (th -pi)(R2 -у2)/(4р1).

В случае турбулентного течения распределение скоростей по поперечному сечению кровеносного сосуда становится существенно более равномерным (рис. 6,6). Это происходит потому, что в турбулентной среде производится гораздо более интенсивный обмен импульсами в поперечном направлении и реализуется существенное перемешивание разных слоёв текущей крови. Уровень турбулентного обмена на много порядков превышает уровень молекулярного обмена, определяющего ламинарное течение.

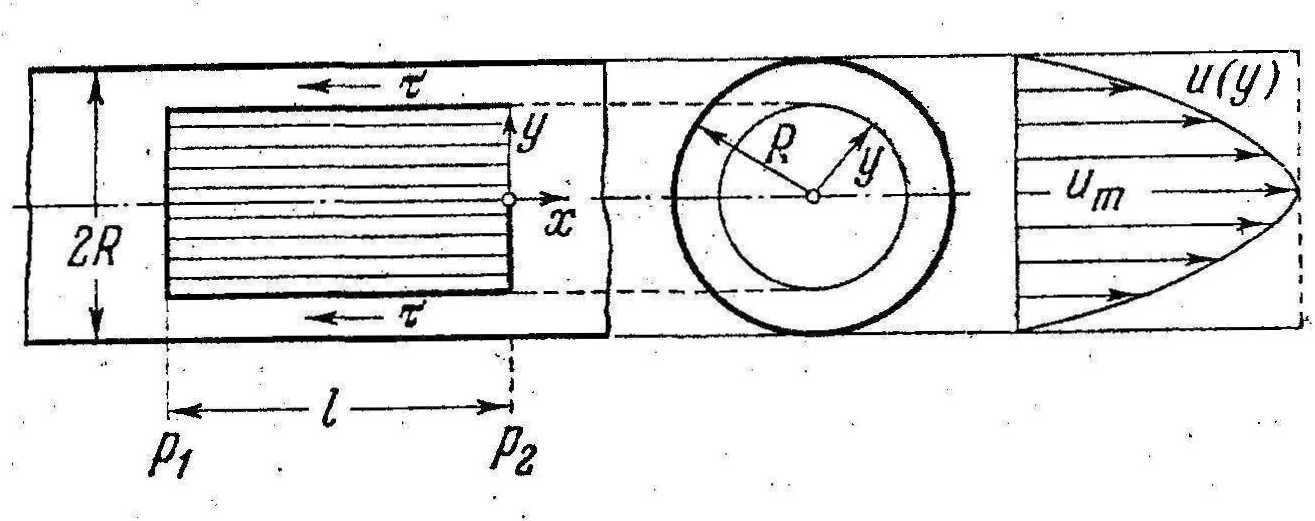
Рис.5. Ламинарный режим течения крови

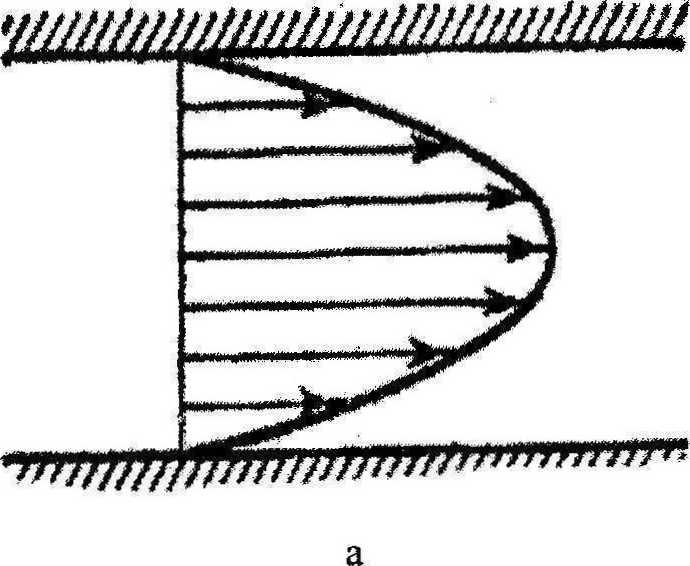
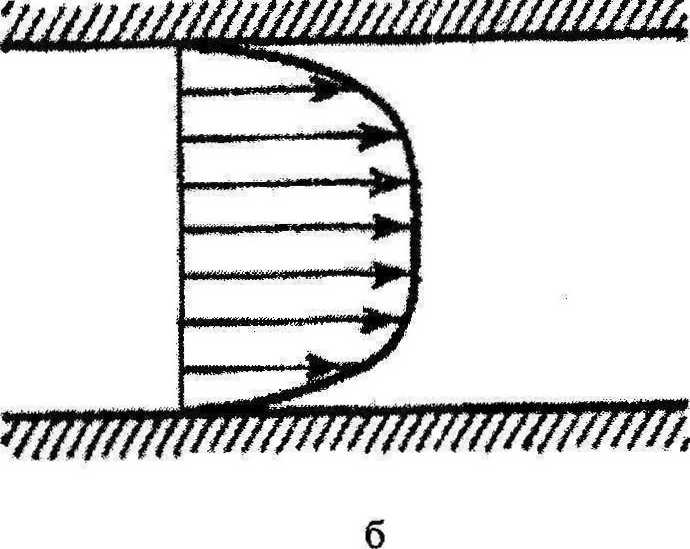
Рис.6. Распределение скорости течения крови по радиусу кровеносного сосуда: а) для ламинарного (параболическое распределение) и б) для турбулентного течений

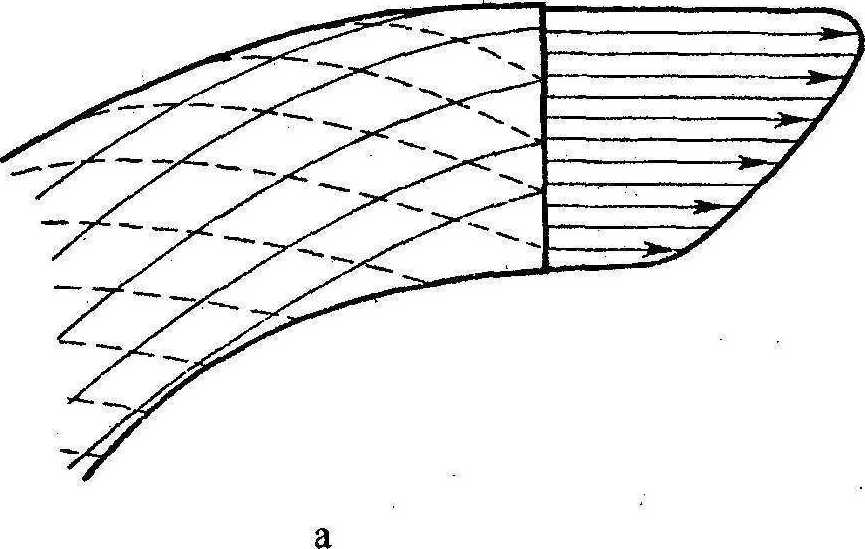
Рис.7. Распределение скоростей течения крови на криволинейных участках кровеносных сосудов: а) в диаметральном и б) в поперечном сечениях

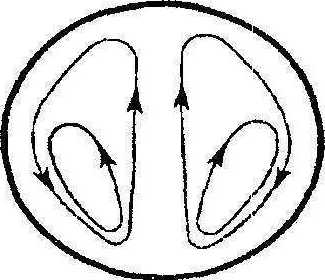
На криволинейных участках кровеносных сосудов характер течения крови существенно усложняется. На рис. 7 приведено распределение скоростей в диаметральном сечении на изогнутом участке кровеносного сосуда (левая часть рисунка). В правой части этого же рисунка показана структура течения крови в поперечном сечении. Вследствие вязкостного пристеночного торможения скорость течения крови вблизи стенок кровеносного сосуда меньше, чем в его середине. Поэтому величина центробежной силы, действующей на частицы крови на изогнутом участке, больше для быстрых частиц крови, первоначально движущихся в середине кровеносного сосуда. Из-за этого возникает вторичное течение, направленное от внутреннего к внешнему радиусу в середине кровеносного сосуда и от внешнего радиуса к внутреннему радиусу на периферии кровеносного сосуда (см. рис. 7). При этом распределение скоростей в диаметральном сечении качественно меняется: максимум продольной скорости смещается из центра кровеносного сосуда к его наружному радиусу (см. рис.7).