Численное моделирование начальной стадии возникновения восходящего закрученного потока

При описании сложных течений политропного сжимаемого газа, обладающего вязкостью и теплопроводностью, используется полная система уравнений Навье-Стокса, которая в безразмерных переменных с где значения безразмерных положительных постоянных коэффициентов вязкости и теплопроводности следующие:

^ = 0 . 001 , к = 0 . 00145833

Эта система в дифференциальной форме передает законы сохранения массы, импульса и энергии в движущейся сплошной среде. В системе (1):

t - время;

x , y , z - декартовы координаты;

p - плотность газа;

V = ( u , v , w ) - вектор скорости газа с проекциями на соответствующие оси;

T - температура газа;

g = ( 0,0, - g ) - вектор ускорения силы тяжести;

• - 2 0 X V = ( av - bw , - au , bu ) - вектор ускорения силы Кориолиса, где a = 2 0 sin у , b = 2 0 cos y ;

—

• О - вектор угловой скорости вращения Земли;

• у - широта точки О - начала декартовой системы координат Oxyz , вращающейся вместе с Землей;

V и div - операторы градиента и дивергенции по декартовым пространственным переменным. Функции u = 0, v = 0, W = 0,     (2)

T 0 ( z ) = 1 - kz ; k = lx ⁰⁰,

T ₀₀

l = 0.0065 K , X ₀₀ = 10⁵ м , T _oo = 288 ^oK (3) м

• ^и p ₀ ( z ) = (1 - kz ) ^{v - 1};   v = ^g = const > 0    ⁽⁴⁾

задают точное решение [3] системы (1) и используются в качестве начальных условий при описании течений сжимаемого вязкого теплопроводного газа в случае постоянных значений коэффициентов вязкости и теплопроводности.

Расчетная область представляет собой прямоугольный параллелепипед с длинами сторон x ⁰ = 1 , y ⁰ = 1 и z ⁰ = 0.1 вдоль осей Ox , Oy и Oz соответственно.

Для плотности на всех шести гранях параллелепипеда:   x = 0 , x = x 0 , y = 0 , y = y 0 , z = 0 ,

Z = Z - ставится «условие непрерывности» потока [4], которое означает, что значения искомой функции на границу области сносятся линейной интерполяцией по нормали к данной граничной поверхности из внутренней части расчетной области.

Краевые условия для компонент вектора скорости газа берутся соответствующими «условиям непротека-ния» для нормальной составляющей вектора скорости

интерполяцией по значениям функций в двух точках вдоль каждого из трех ребер.

Расчеты начальной стадии формирования восходящего закрученного потока [5-7] проводились при следующих входных параметрах: масштабные размер-

ные значения плотности, скорости, расстояния и вре-

мени равны соответственно

P 00 = 1.2928 y-3 ,

и «условиям симметрии» для двух других компонент вектора скорости течения. А именно:

f § = 0, § = § ⁰    0,

dg д§

= 0, § = 0, §=§ ⁰

u ₀₀ = 3 3 3—, ^x 00    ¹⁰⁰⁰⁰⁰ /' , t 00 = ^x 00 / u 00 = 300.3 c .

Разностные шаги по трем пространственным переменным A x =A y = A Z = 0.01 , а шаг по времени

где f – нормальная составляющая вектора скоро сти газа к поверхностям § = 0, § = §0 , а g - две дру-

гие составляющие вектора скорости газа, то есть тан-

генциальные по отношению к поверхностям § = 0, § = § 0 .

Для температуры на пяти гранях задаются условия теплоизоляции

d т

д§

= 0.    (6)

§ = 0, § = § ⁰

A t = 0.001 , модуль угловой скорости вращения Земли Q = 0 . 0218 .

На рис. 1 представлен график функции температуры для плоскости Z = 0 и для 1000 расчетного шага по времени. Нагрев поверхности Z = 0 осуществлялся в соответствии с формулой (7) до температуры Т = 1.125 (размерное значение 324 ° K = 51 o C ).

На рис. 2 приведен график функции плотности газа на плоскости Z = 0 и для 1000 расчетного шага по времени. В центре нагрева наблюдается область пониженной плотности.

На плоскости Z = 0 значения температуры заданы в виде функции [8]

Т^₀ = Т _о( t , x , y ) = 1 + 0.125 ( 1 - e⁴⁰t ) cos⁶ ^ nJ ( x - 0.5 ) 2 + ( y - 0.5 ) 2 j

,      (7)

которая моделирует локальный нагрев поверхности Земли.

Расчетная область заполняется трехмерной сеткой узлов пересечения трех семейств плоскостей x = X i, y = yj , Z = Zk, где Xi = i-Ax , yj = j-Ay, Zk = k-Az, 0 < i < L , 0 < j < M, 0 < k < N.

Ax = X 0/ L , Ay = y0/ M, Az = z0/ N - разностные шаги по трем пространственным переменным.

Зная в начальный момент времени во всех точках прямоугольного параллелепипеда все искомые функции с помощью явной разностной схемы вычисляются значения искомых функций во всех внутренних точках прямоугольного параллелепипеда.

После этого искомые функции определяются во всех внутренних точках каждой из шести граней: x = 0 , x = x ⁰, y = 0 , y = y ⁰, Z = 0 , Z = Z 0 .

Значения искомых функций во внутренних точках всех двенадцати ребер прямоугольного параллелепипеда находятся как среднее арифметическое двух промежуточных значений, определенных линейной интерполяцией по значениям функций в двух точках на нормалях к ребру в каждой из граней.

В вершинах прямоугольного параллелепипеда значения берутся как среднее арифметическое трех промежуточных значений, определенных линейной

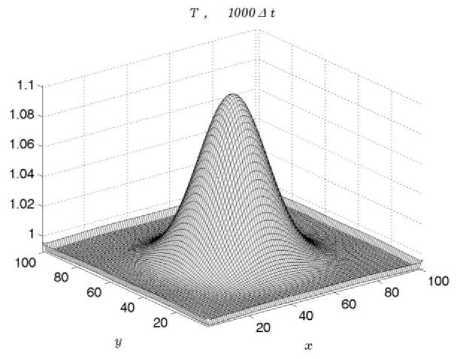
Рисунок 1

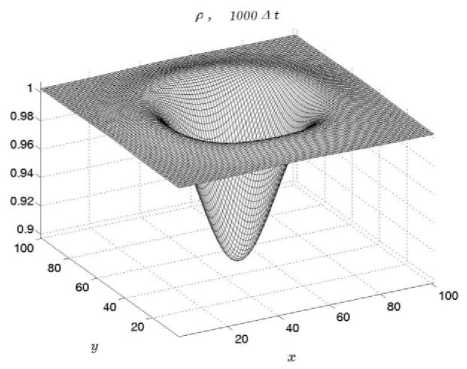
Рисунок 2

На рис. 3-5 даны графики функций для трех компонент скорости в нижней части расчетной области на 1000 расчетном шаге по времени.

и, 1000 Д t

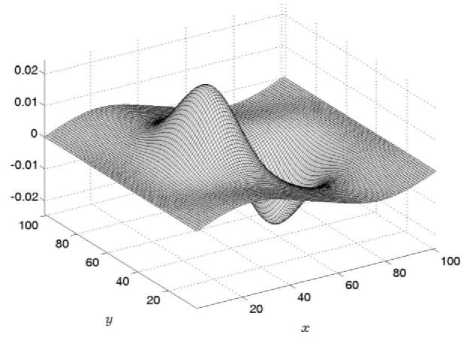
Рисунок 3

в, 1000J I

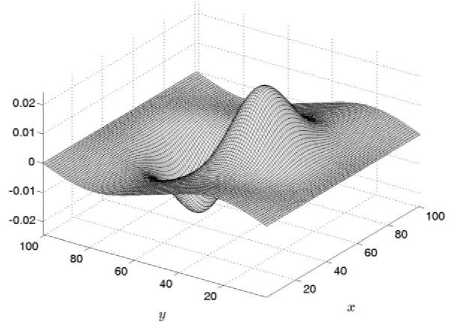
Рисунок 4