Численное моделирование напряженно-деформированного состояния многослойного аэродромного покрытия

4 α ⋅ θ ⋅ E

σ= 1-ν , где а - линейный коэффициент температурного расширения; 9 - максимально возможное падение температуры за 1 ч; ν – коэффициент Пуассона (учитывался не всегда).

Предложенная зависимость (1) была усовершенствована Н.В. Горелышевым в работе [4], где косвенно учитывалось явление релаксации:

σ =

4 ⋅ ( α ⋅ θ ⋅ E - m ⋅ ε n )

1 - ν

где ε n – ползучесть асфальтобетона; m – коэффициент пропорциональности.

Позднее А.Р Красноперов [5], используя способ определения температурной трещино-стойкости асфальтобетонного слоя усиления с учетом длины участка свободного контакта, установил аналитическую зависимость для определения полных температурных растягивающих напряжений в покрытии:

σ

полн .

п

α o Δ Т o - τ o L + 2 τ п l o 2 h o E o 1 E п ( L 2 l o - 1 ) + h п h o Ε o

+ βα п ⋅Δ Т п ⋅ Е п

где о_п полн - полные (собственные и за счет основания) температурные растягивающие напряжения в покрытии; α_о и α_п – линейные коэффициенты температурного расширения основания и покрытия соответственно; h _о и h _п - толщины основания и покрытия; Е _о и Е _п - расчетные модули деформации основания и покрытия; ∆ Т _о и ∆ Т _п – расчетные перепады температур основания и покрытия; L – длина плит основания; l о – длина скользящего контакта покрытия с основанием (на одном крае плиты); β – поправочный (понижающий) коэффициент, отражающий степень податливости соединения покрытия с основанием; τ о и τ п – осредненные напряжения трения на границе с основанием и покрытием.

В ВСН 197-91 представлена методика расчета напряжений о в зависимости от температурного градиента в нижележащем слое A T_inf :

с =

c • E -A T i„f

2       ^,

где

^- h sup

A T ,= A • e inf п

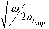
^- h sup

1 - e

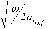
где Ап - перепад температуры в течение суток на поверхности асфальтобетонного покрытия, oC; го - угловая частота суточных колебаний температуры, рад/ч, го = 0,26 рад/ч; at = 0,002 м2/ч и a = 0,004 м2/ч - коэффициенты температуропроводности соответственно асфальтобетона и tinf цементобетона.

Обобщением и анализом приведенных методик установлено, что все они не свободны от недостатков. Во-первых, не учитывается изменение температурных полей по глубине многослойной конструкции. Во-вторых, в расчетах игнорируются касательные напряжения, возникающие на границе сращивания слоев покрытия и/или основания. В-третьих, аналитические – 1256 – зависимости не учитывают динамического изменения значений физико-механических характеристик асфальтобетона, обусловленного сезонным градиентом температуры.

В связи с этим методика прогнозирования изменения НДС асфальтобетонных слоев наращивания сборных аэродромных покрытий, учитывающая динамическое изменение значений физико-механических характеристик асфальтобетона вследствие сезонного градиента температуры, требует дальнейшего совершенствования.

Процесс образования трещин в асфальтобетонных слоях усиления можно описать с использованием различных теорий: теории упругости; теории, основанной на критерии Мизеса; метода Шмидта; теории, разработанной в центральной лаборатории мостов и дорог Франции, и др. [6-8]. Указанные теории в той или иной степени учитывают градацию состояния асфальтобетона от вязко-упругого до хрупкого.

Очевидно, что при отрицательной температуре асфальтобетон перестает быть пластичным и возможен переход к твердому хрупкому состоянию. При определенных условиях, например при Т в < минус 20 ^оС асфальтобетон приобретает свойства сплошного твердого тела. Указанное обстоятельство определяет возможность применения положений теории упругости для моделирования НДС многослойного аэродромного покрытия в условиях градиента температуры путем решения квазистатической задачи термоупругости, без учета эффекта связности полей температур и деформаций, а также сил инерции, обусловленных нестационарным температурным полем.

Модельное представление аэродромного покрытия - многослойный упругий пакет, лежащий на жестком основании. Пакет состоит из асфальтобетонного слоя и трещиновато-блочного основания, инициатора трещин.

В общем случае при температурно-зависимом изменении НДС трехмерного твердого тела, свободного от внешних механических воздействий (объемные силы не учитываются), возникают перемещения и , и и w [9].

При модельном представлении в аэродромном покрытии выделяется плоскость единичной толщины dh (рис. 1). Допущение: мгновенная температура dT в момент времени dτ ввиду малой толщины плоскости стационарна ( T_dh = const). Поскольку размеры рассматриваемых единичных плоскостей в плане многократно превышают толщину, то перемещения любой точки будут происходить исключительно вдоль осей x и у, а перемещениями вдоль оси h можно пренебречь:

и = и ( x,у, т ), и = и (x,у, т ), w = 0.

Тогда зависимость относительных деформаций от перемещений принимает вид

e

x

ди т", e У дx

d u         д и  d u

—, g xy =—+— , e h = g yh = g hx = ° д y       d y   д x

где e x , e y , e_h , - относительные деформации; y xy , Y yh , Y hx , - угловые деформации.

Выделим единичный блок в плоскости аэродромного покрытия со сторонами dx, dy, dh (рис. 1). Воздействие температурного поля формирует в покрытии плоское деформированное состояние с составляющими деформации: Adx , Ady и Y xy . При наличии указанных деформаций в элементарном объеме будут возникать нормальные и касательные напряжения o_x, о_у и T xy .

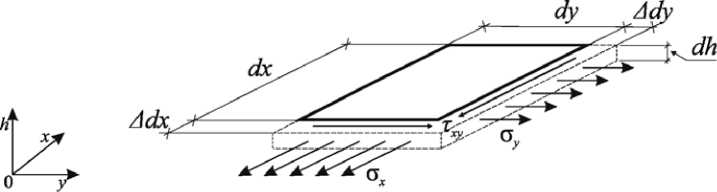
Рис. 1. Расчетная схема единичного слоя

Относительные тепловые деформации элемента е в соответствии с гипотезой Неймана таковы:

e XT ⁾ = e (T ⁾ = a T ,                                                                     (8)

где a - линейный коэффициент температурного расширения; Т - температура единично- ( T ) _Л( T )

го объема; e _х , e у - относительные тепловые деформации в декартовой системе координат.

При неравномерном нагреве (охлаждении) упругого тела, а также при закреплении одной из его сторон в нем возникают термоупругие напряжения, обусловленные несвободным расширением (сжатием). Общая деформация на основании соотношений Дюамеля - Неймана будет складываться из связи термоупругих напряжений и деформаций и выражаться следующими равенствами:

E x = |( a - va y ) + a T , E y = |( a y -vo, ) + a T , ₇ y = 1 t„ ,                 (9)

EEG где Е - модуль упругости; v - коэффициент Пуассона; G = Ej2(1 + v) - модуль сдвига.

Выразив из (9) напряжения через деформации, получим:

o x = 2 G e x + Z e - (3Z + 2 G ) a T, o _y = 2 G e y + Ze - (3Z + 2 G ) a T , T xy = G T ^ ,

где Z = 2 v G, 1 - 2 v - коэффициент, не зависящий температуры; е - объемная деформация [9].

Уравнения равновесия для случая плоской задачи имеют вид

Во дт Во  Вт

--x_ + _^L = 0,   y + _2y. = 0.

В x    В y         B y    В x

Подставив выражение (10) в (11) с использованием (7), выразим относительные и объемные деформации через перемещения.

В результате получим общую закономерность развития деформации слоя аэродромного покрытия, свободного от внешнего механического воздействия, в условиях нестационарного температурного поля с учетом динамики изменения характеристик материала конструкции:

д Т д x	=-----1----- (3Х+2 G ) а	■ Г G )	д д x	ди ди' д x + д у	1+ G	д 2 и + д 2 и дд?
д Т д у	=-----1----- (3Х+2 G ) а	■ (l+ G )	д д у	д и ди д x + д у	1 + G'	д 2 и д2и д x 2 д у2

где T - распределение температуры в слое аэродромного покрытия; и и и - перемещения относительно осей x и y соответственно; λ - коэффициент, не зависящий температуры; G - модуль сдвига.

Левая часть выражения (12) описывает температурное поле конструкции, а правая - деформации, возникающие при воздействии указанного поля, с учетом термоупругих характеристик материала конструкции слоя. Решение уравнения (12) при учете реальных начальных и граничных условий аналитическим путем является громоздким и сложным. В связи с этим решение реализовано методом конечных элементов в форме метода перемещений элемента в программном комплексе COMSOL Multiphysics в соответствии с разработанным алгоритмом, представленным на рис. 2.

В программном комплексе используется итеративная процедура метода Ньютона - Раф-сона, объединяющая тепловой и прочностной анализы и предусматривающая совместное термопрочностное решение, обусловленное наличием как тепловых, так и прочностных степеней свободы конечных элементов.

Средства термопрочностного анализа программы COMSOL Multiphysics позволяют использовать результаты решения задачи теплообмена при оценке НДС конструкции. Тепловая нагрузка задана как определяющая. Последовательными итерациями уточняется совместное решение тепловой и прочностной задач, пока не будет достигнут установленный критерий сходимости решения. Сходимость контролируется по величине невязки вектора нагрузок (потока тепла) и/или по изменению температуры от итерации к итерации. Для производства расчетов использовали модули Geomechanics (геомеханика), Heat Transfer (теплоперенос) и Radiation (радиация), тип расчета - Time Dependet (нестацио-нарный).

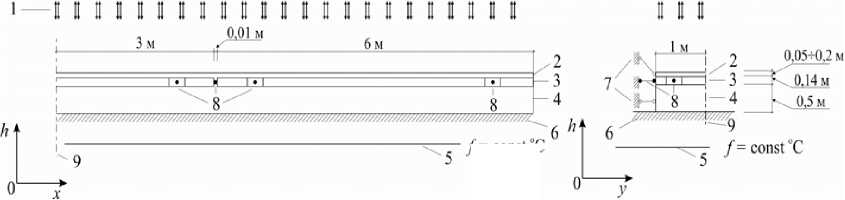
В качестве объекта моделирования принята конструкция аэродромного покрытия, включающая: слой усиления из плотного асфальтобетона; сборное аэродромное покрытие из плит ПАГ-14; слой щебеночного искусственного основания. Значения физико-механических характеристик материалов слоев аэродромного покрытия представлены в табл. 1.

Варьируемым параметром, оказывающим влияние на температурный режим и изменение напряженно-деформированного состояния конструкции в целом, назначили толщину асфальтобетонного слоя. Параметр варьировали от 0,05 до 0,2 м.

Расчетная схема многослойного аэродромного покрытия с введенными допущениями моделирования представлена на рис. 3. Расположение подошвы и кровли слоев основания задано горизонтальным. Нижняя граница основания жестко закреплена, что исключает горизонтальные и вертикальные перемещения и вращение участка. В расчетах учтен собственный вес покрытия. Выравнивающую прослойку в модели не учитывали. Передача усилий между плитами в деформационных швах осуществляли посредством введения шарниров, расположенных в местах стыковых и монтажных соединений.

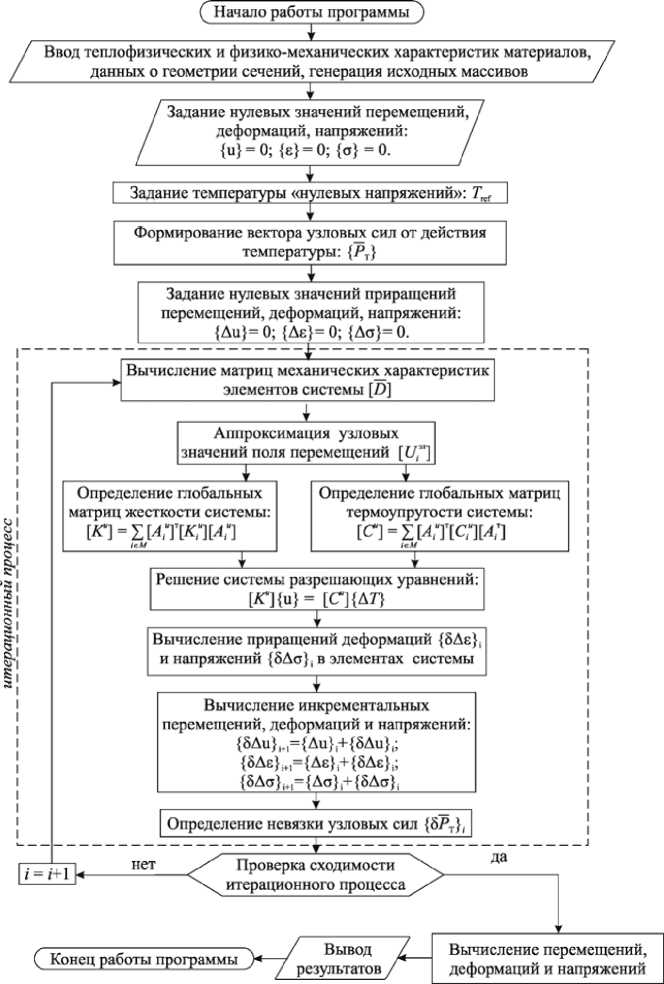
Рис. 2. Алгоритм моделирования НДС конструкции аэродромного покрытия

Неподвижность во всех направлениях по левой и нижней границам участка обеспечивали введением жесткой заделки.

Моделирование производили с численными данными, приведенными в табл. 2 [10].

В ходе численного моделирования приняты следующие допущения: начальная температура покрытия до линии нулевых температурных колебаний одинакова; конвективный и радиационный теплообмен происходит только через верхний слой покрытия; материал покрытия термоупругий; температура нулевых напряжений 5 оС [13]; контакты между слоями идеальные.

Таблица 1. Значения физико-механических характеристик слоев аэродромного покрытия

Наименование слоя	Толщина слоя, м	Плотность, кг/м3	Модуль упругости, МПа	Коэффициент Пуассона	Теплопроводность, Вт/(м·0С)
Асфальтобетон плотный мелкозернистый на битуме БНД 60/90	0,05…0,2	2100	3200	0,3	0,9
ПАГ-14	0,14	2500	30400	0,2	1,86
Щебень фракционированный	0,5	1800	400	0,25	0,11

/= const С

Рис. 3. Расчетная схема моделирования теплового воздействия и изменения НДС многослойного аэродромного покрытия: 1 – факторы, воздействующие на покрытие; 2 – асфальтобетонный слой усиления; 3 – плита ПАГ; 4 – щебеночное основание; 5 – линия нулевых температурных колебаний; 6 - жесткая заделка; 7 – подвижные шарниры; 8 – неподвижные шарниры (сварные соединения); 9 – ось симметрии

Таблица 2. Исходные данные для проведения расчетов

Параметр	Значения
Местоположение	Россия, Ленинградская область
Координаты	60о06’11” с.ш. 30о12’27” в.д.
Месяц/2015 г.	январь
Часовой пояс	+4
Цикл измерений, ч	24 ч
Тепловой поток солнечного излучения, Вт/м² [11]	1000
Глубина затухания колебаний температуры, м [10]	0,8
Температура на глубине, оС [10]	2,2
Коэффициент поглощения солнечной радиации [12]	0,89
Коэффициент поверхностного излучения [12]	0,93
Коэффициент, учитывающий ослабление солнечного облучения вследствие запыленности приземной атмосферы воздуха [12]	0,6
Характеристики режима отрицательной температуры, оС	Т в ср = – 7,9; ∆T в min = 0,8; ∆T в max = 15,1

Моделирование осуществлялось поэтапно. На первом этапе моделировали распределение температурных полей в многослойном аэродромном покрытии, на втором этапе – напряженно-деформированное состояние. Моделирование температурных полей производилось за 24-часовой цикл для трех температурных режимов в две стадии. На первой стадии задавали внешние факторы воздействия, начальные условия и формировалась исходная матрица температур по толщине. На второй стадии решалась задача определения полей распределения температуры в толще аэродромной конструкции при лучисто-конвективном обмене верхнего слоя с воздушной средой.

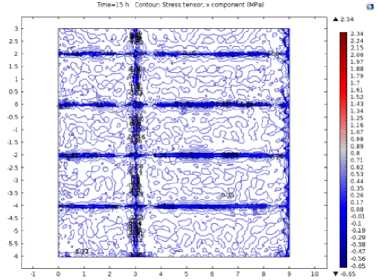
В результате моделирования получили распределение температуры по толщине аэродромного покрытия, значения нормальных и касательных напряжений в слоях конструкции и величины деформаций железобетонных плит покрытия, обусловленные градиентом температуры. Графически результаты численного моделирования представлены на рис. 4 и 5.

Анализом результатов моделирования установлено, что асфальтобетонный слой усиления в пределах границы контакта с железобетонной плитой независимо от толщины в течение 24-часового цикла испытывает растягивающие напряжения, изменяющиеся по гармоническому закону. С увеличением толщины слоя наращивания диаграмма изменения напряжений практически совпадает с диаграммой изменения температуры воздуха.

Рис. 4. Объемные деформации конструктивных слоев аэродромного покрытия в районе шва

а)

Изополя напряжений в плоскости

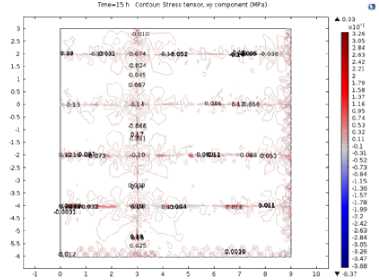
б)

аэродромного покрытия: а - нормальные напряжения;

Рис. 5.

б - касательные напряжения

Касательные напряжения в центре и на боковых гранях плиты близки к нулю и изменяются в пределах от минус 0,01 до плюс 0,23 МПа. Концентрация наблюдается в угловых участках плит (рис. 5 б ), максимальные значения напряжений преобладают в утреннее время и могут достигать 2,52 МПа. Максимальные нормальные напряжения в зоне контакта слоев концентрируются над поперечным деформационным швом сборного аэродромного покрытия, по остальной площади распределены равномерно, что объясняется собственными температурными напряжениями. Амплитуда колебания нормальных напряжений сдвинута во времени по отношению к изменению температуры воздуха. Установлено, что с увеличением толщины слоя наращивания максимум напряжений по времени наступал позднее (рис. 6). Значения напряжений изменялись в интервале от 0,2 до 11,02 МПа соответственно увеличению толщины слоя усиления и глубине места измерения. Установлено, что на глубине 35 см и более напряжения в покрытии стремятся к нулю. Напряжения в покрытии от воздействия температуры по глубине конструкции изменялись неоднозначно. В железобетонной плите наблюдалось незначительное возрастание напряжений практически по линейному закону, при этом напряжения увеличивались от 0 до 3,6 Мпа.

На границе сращивания двух слоев отмечали скачок напряжений, обусловленный различием значений физико-механических характеристик используемых материалов. При этом величина скачка напрямую зависела от толщины слоя усиления: при H sup = 5 см , a max = 11,02 МПа; H_sup = 13 см , σ_max = 7,32 МПа; H_sup = 20 см , σ_max = 1,63 МПа. Графическая интерпретация полученных результатов представлена на рис. 6.

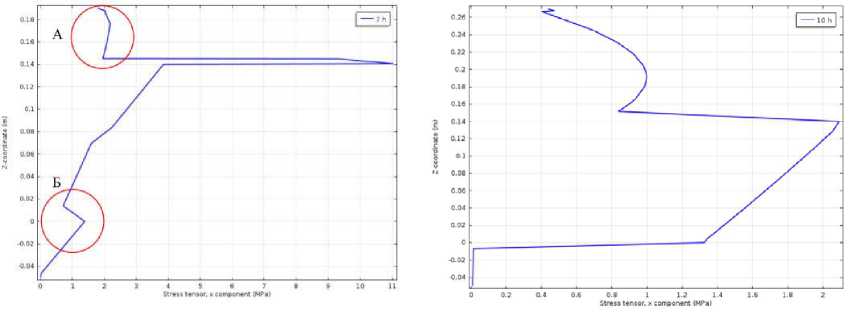
Моделирование позволило установить, что в асфальтобетонном слое в зависимости от времени наблюдения (период нагрева или охлаждения) могут возникать как растягивающие, так и сжимающие напряжения, величина которых зависит от толщины слоя и температуры воздуха. Значения напряжений, например в узле А, изменяются от минус 1,35 до 2,61 МПа (рис. 7 а ). Незначительное скачкообразное увеличение напряжений на границе контакта железобетонной плиты и искусственного основания (в пределах 1 МПа) обусловлено наличием сил трения т _осн.

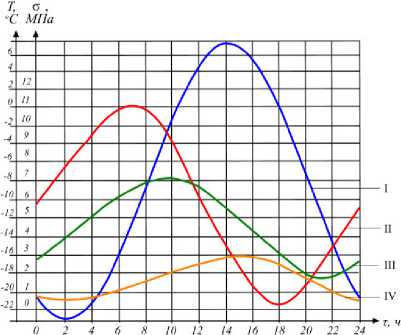
Рис. 6. Динамика изменения нормальных напряжений на границе контакта слоев в покрытии за 24-часовой цикл: I – температура воздуха; II, III, IV – напряжения при H_sup = 5, 13 и 20 см соответственно

Однако в целом на динамику развития деформаций указанное обстоятельство влияния не оказывало. Это проиллюстрировано ломаной кривой в районе узла Б на рис. 7 а .

Аналогичная картина наблюдалась и в центре плиты, хотя скачка напряжений на границе контакта плиты и искусственного основания не было. В то же время на границе контакта со слоем наращивания напряжения значительно ниже, чем на краевых участках. Это свидетельство того, что деформации в железобетонной плите происходят относительно виртуального неподвижного центра, в котором касательные напряжения минимальные, а напряжения в асфальтобетонном слое вызваны только собственными температурными деформациями.

Отсюда следует, что рост напряжений в асфальтобетонном слое над краем железобетонной плиты обусловлен градиентом напряжений по толщине покрытия в целом. Указанное обстоятельство проиллюстрировано на рис. 7 б .

Деформации железобетонных плит при температурном воздействии аналогичны напряжениям, развиваются по закону, близкому гармоническому, и следуют за ходом температуры в покрытии с выраженными максимумами и минимумами. Динамика процессов, происходящих в теле многослойного аэродромного покрытия за 24-часовой цикл при H sup = 20 см, представлена на рис. 8.

Показано, что значения деформаций уменьшаются при увеличении толщины асфальтобетонного слоя. Так, при H sup = 5 см А 5 = 0,054 мм, а при H sup = 20 см - А 5 = 0,031 мм. С увеличением толщины верхнего слоя температурный градиент искусственного основания оказывает влияние на диаграмму деформирования плит ПАГ в большей степени, чем градиент температуры наружного воздуха. Если при H sup = 5 см максимальное значение деформации соответствует максимальной температуре на границе сращивания слоев покрытия, то при H sup = 20 см эти показатели не соответствуют друг другу и максимальное удлинение плиты наблюдается до достижения максимума температуры покрытия. При достижении максимальной температуры деформации плит изменяют знак.

Таким образом, установлена закономерность развития деформаций слоя усиления аэродромного покрытия, свободного от внешнего механического воздействия, при нестационарном

а)                                                    б)

Рис. 7. Распределение нормальных напряжений по глубине при расположении точки измерения у торца плиты и H sup = 5 см (а), при центральном расположении точки измерения и H sup = 13 см (б)

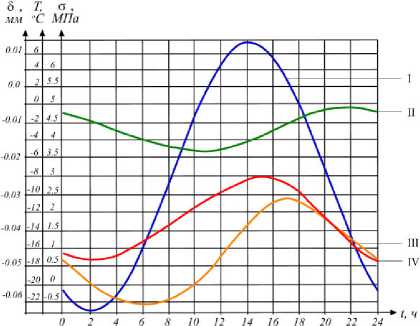
Рис. 8. Динамика процессов, происходящих в теле многослойного аэродромного покрытия за 24 часовой цикл при Hsup = 20 см: I - температура воздуха; II - температура на границе контакта слоев; III – деформации; IV – нормальные напряжения градиенте температуры, с учетом термоупругих характеристик материала конструкции, смоделирован процесс изменения НДС слоистой конструкции во времени и по глубине и оценено влияние толщины асфальтобетонного слоя на динамику развития напряжений и деформаций в указанном слое.