Численное моделирование нейронной сети на основе модели Ходжкина-Хаксли

Нейрон — основной функциональный элемент нервной системы. Типичный нейрон состоит из трех частей: тела, дендритов и аксона. Дендрит принимает сигналы от другого нейрона, а аксон передаёт их другим нейронам. Место контакта аксона одного нейрона и дендрита другого нейрона называется синапсом. Сигналы, принимаемые с дендритов, суммируются в теле нейрона и если данная сумма превышает определённый порог, то возникает нервный импульс или спайк [1]. Кроме возбуждения нейроны могут и тормозить друг друга, уменьшая "сумму" внутри нейрона и препятствуя возникновению спайка.

Оболочка нейрона является хорошим изолятором, поэтому ионные составы вне и внутри нейрона различны. Заряженные частицы переносятся между внутренностью нейрона и окружающей его межклеточной жидкостью с помощью так называемых ионных насосов (существует, например, натрий-калиевый насос). Импульсы от возбуждающих и тормозящих 1

нейронов, приходящие к нашему нейрону, "включают" разные виды ионных насосов. Так регулируется электрическое поле нейрона. В зависимости от того, каким оно будет, импульс либо побежит дальше, либо нет.

Постановка задачи. На данный момент созданы различные как относительно простые модели, например, «Inregrate and Fire», в которой нейрон представляется в виде конденсатора и резистора, так и более детальные, биологически правдоподобные, модели, например, модель Ходжкина-Хаксли, которая гораздо сложнее как в вычислительном плане, так и в плане анализа её динамики, но она гораздо точнее описывает динамику мембранного потенциала нейрона [2].

Классическая модель Ходжкина-Хаксли описывается следующей системой дифференциальных уравнений [3]:

ь т

dV _

Hi = Iext

+ ^ syn ⁽ⁱ⁾

- ^G Na

- ^G k ^{- G} L ,

dm dt dh dt dn dt

a(V)(1 - m) - fi m (V)m, a_h(V)(1-h)-^_h(V)h, a n (V) ⁽ 1 - n) - 0 n ⁽ V)n,

где

^ m (V) =

0.1(25-V)

exp(25 - V)

10       1

PmW = ^4ex P (^-^);

^ h ⁽ V) = 0.07exp (- ^V );

MV =

(30 - V\ ;

1 + exp (-IT)

• ₄    0.01(10-V)

an(V) = “   (10-V\’

• ^{1    + exp} ("ttJ ^ n (V) = 0.125exp(- ^V ); ^G Na = 9 Na ^m3h(V ^{- V} Na ^{); G} K = 9 K ⁿ 4 ^{(V - V} K ^);

^G L = 9 l ^{(V - V} L ).

Начальные условия для системы (1) имеют вид

V(0) = V0; m(0) = m0; h(0) = h0;n(0) = n0.

Здесь V(t) — мембранный потенциал , m(t), h(t), n(t) - так называемые воротные переменные: т, п - активационные переменные для калиевых и натриевых каналов, h -инактивационная переменная натриевых каналов. Эти переменные задают изменения проводимости ионных каналов в зависимости от мембранного потенциала, С_т - мембранная емкость. Остальные параметры были получены экспериментальным путем и имеют следующие значения:

g_Na = 120 мСм; д^ = 36 мСм,; g_L = 0,3 мСм;

V_Na = 115 мВ; V_K = -12 мВ; V_L = 10,6 мВ.

Сумма синаптических токов рассчитывается по следующей формуле:

Ne Nt

^I syn = ^С т ^д ехс [ ^ ^ ^{l(t — t} k ^{) —} К ^ ^ l ^{(t — t} m ^)] . k=1 I m=1 n

Здесь N_e - количество возбуждающих нейронов, N- количество тормозных нейронов, l(t — 4) ^и l(t — t m ) - индикаторные функции, принимающие значение 1, если их аргументы равны нулю, и 0 - в противном случае, t k - время разряда I-го спайка к-го нейрона, С_т — мембранная емкость. Константы, д_ехс = 1 и К = 4 вычислены эмпирически.

Численные расчеты получены методом Рунге-Кутты 4-го порядка при t 6 [0, 300] и следующих параметрах: количество возбуждающих нейронов – 200, количество тормозящих нейронов – 50.

Данная модель была реализованы в среде разработки Google Colaboratory. При программировании использовались библиотеки NumPy и SciPy, а также библиотека Matplotlib, позволяющая визуализировать полученные данные.

Рассмотрим случай, когда значение входного тока I_ext принимает значение, равное 5мА.

На рис. 1 представлен график колебаний мембранного потенциала с течением времени, на рис. 2 – график изменения воротных переменных с течением времени, и на рис. 3 – зависимость мембранного потенциала V от времени.

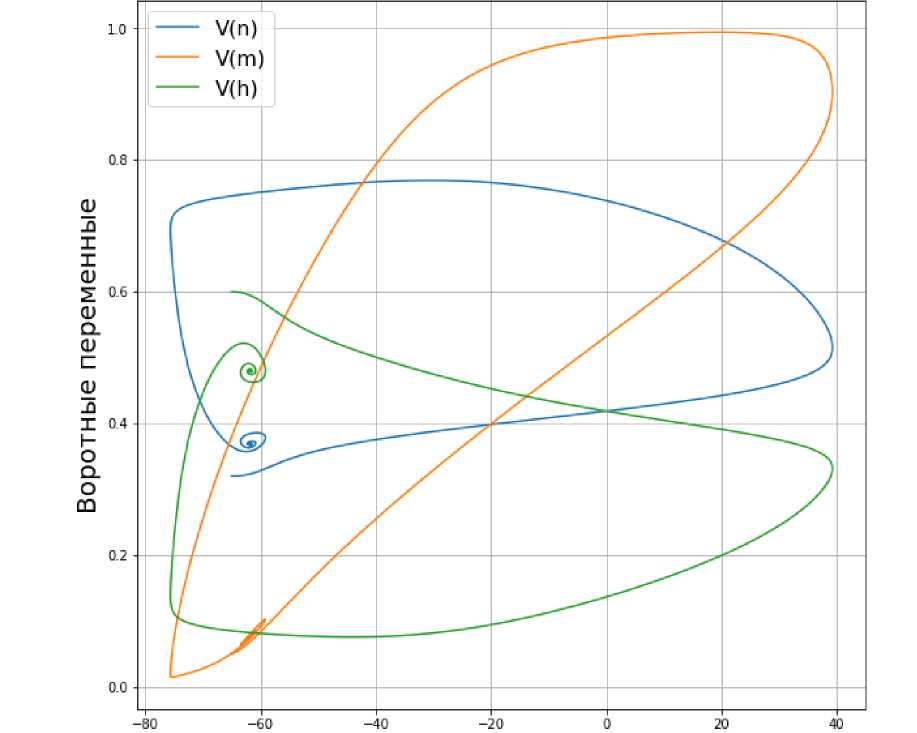
Исходя из данных графиков, можно сделать вывод, что при значении входного тока I_ex t = 5 мА колебания мембранного потенциала исчезают. То же происходит и с воротными переменными. Из рис. 3 видно, что траектория зависимости воротных переменных от мембранного потенциала V не является периодической.

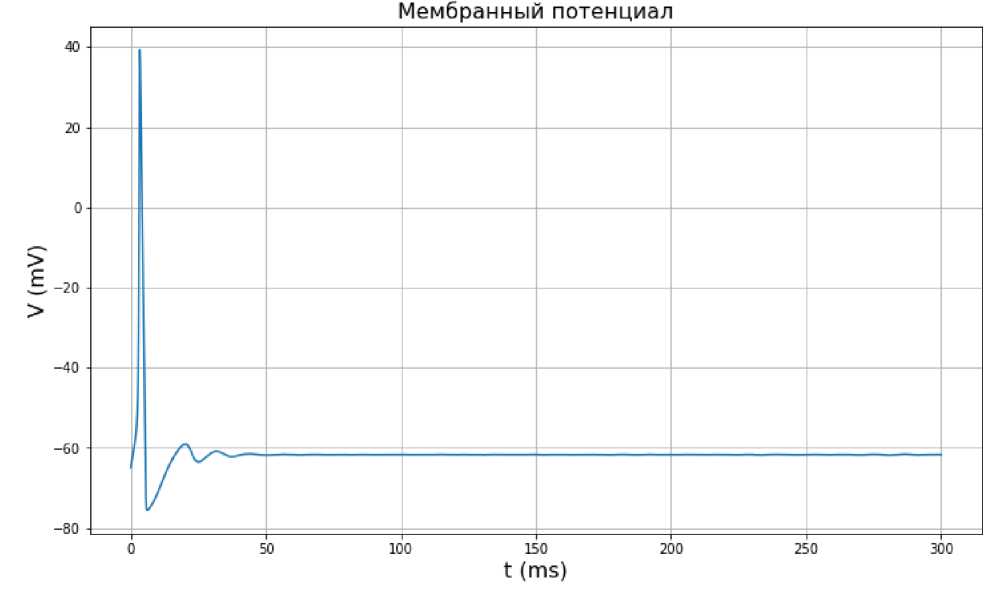
Рис. 1. Зависимость мембранного потенциала V от времени по модели Ходжкина-Хаксли при значении входного тока I _ext = 5 мА.

Воротные переменные

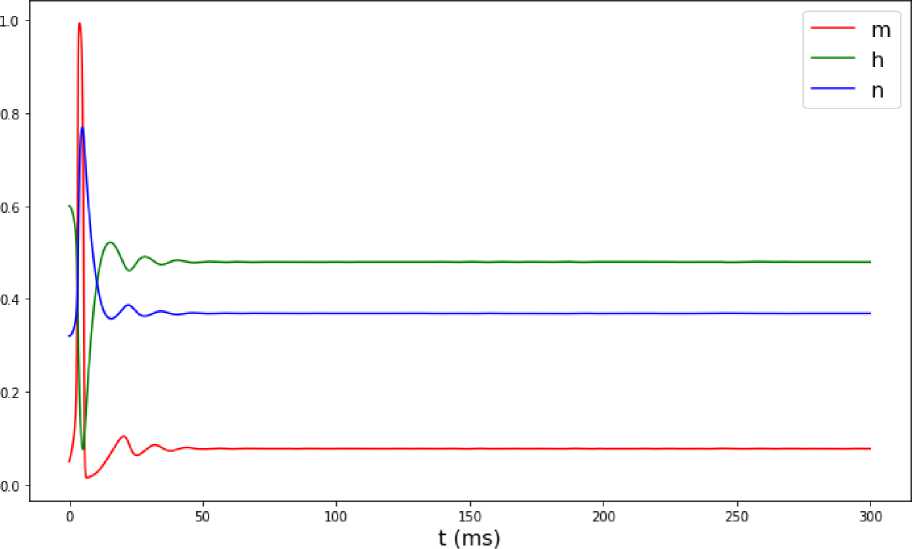
Рис. 2. Изменение воротных переменных с течением времени при значении входного тока Iext = 5 мА.

Мембранный потенциал (V)

Рис. 3. З ависимость воротных переменных от мембранного потенциала V при значении входного тока I_ext = 5 мА.

С другой стороны, если входной ток достигает значения 5 мА, то предельный цикл фактически вырождается. Это значит, что такое значение входного тока слишком мало, чтобы возбудить нейрон.

Увеличим значение входного тока до 10 мА. По графику колебаний мембранного потенциала, представленного на рис. 4, и графику воротных изменения воротных переменных (см. рис. 5), можно предположить, что процесс является периодическим. После 1-2 пиков потенциал стабилизируется. Аналогичным образом ведут себя воротные переменные (см. рис. 5). Можно предположить (см. рис. 6), что траектория з ависимости воротных переменных от мембранного потенциала V представляет собой невырожденный предельный цикл.

Судя по результатам численного эксперимента, при значении входного тока в 10 мА имеем наиболее ярко выраженный предельный цикл. Данное значение является оптимальным для возбуждения нейрона и передачи сигналов от одного нейрона другим.

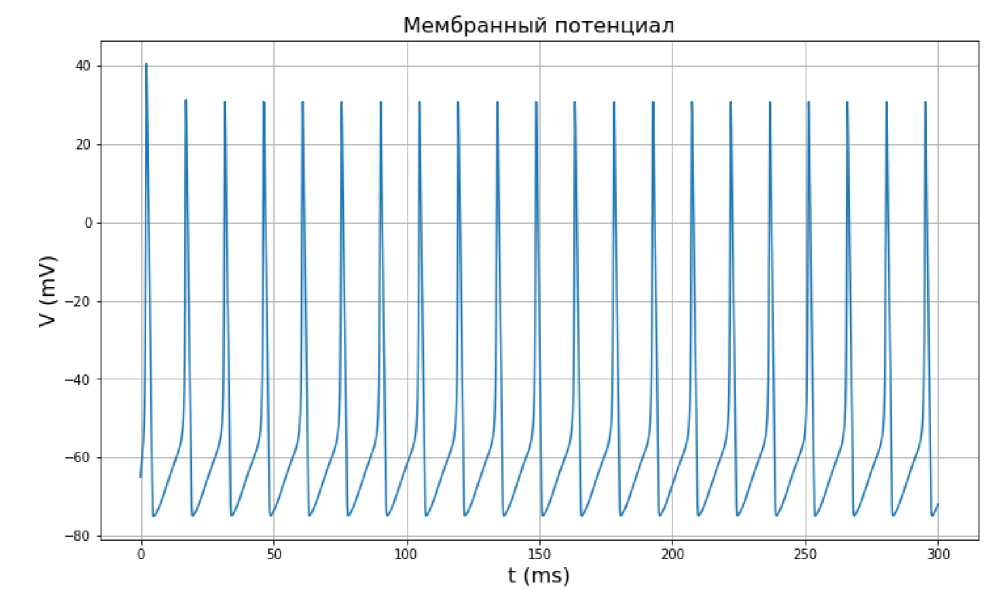
Рис. 4. Зависимость мембранного потенциала от времени по модели Ходжкина-Хаксли при значении входного тока I _ext = 10 мА.

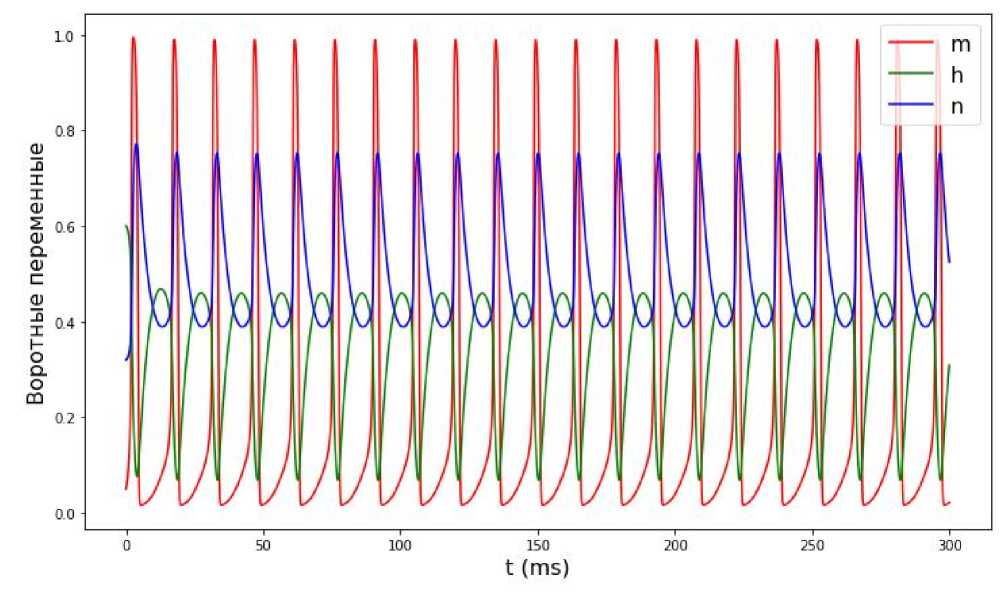
Рис. 5. Изменение воротных переменных с течением времени при значении входного тока I _ext = 10 мА.

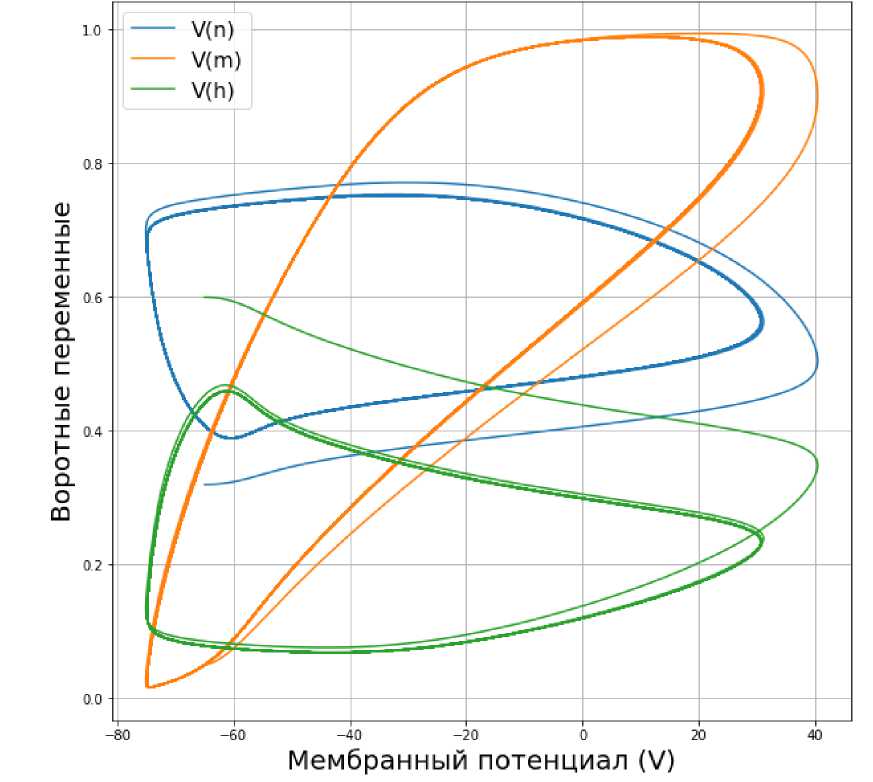
Рис. 6. З ависимость воротных переменных от мембранного потенциала V при значении входного тока I _ext = 10 мА.

Пусть теперь значение входного тока достигает значения I_ext = 50 мА. Если мы посмотрим на графики колебаний мембранного потенциала (рис. 7) и изменения воротных переменных, то увидим, что после первоначального скачка амплитуда колебания мембранного потенциала в периодическом режиме снижается. Это же происходит и с воротными переменными см. (рис. 8). Из рис. 9 следует, что выход на предельный цикл теперь происходит медленнее (траектория делает большее число витков).

При таком значении тока для достижения предельного цикла нужно сделать большее число витков по фазовой траектории. Такое значение входного тока губительно для нейронов головного мозга.

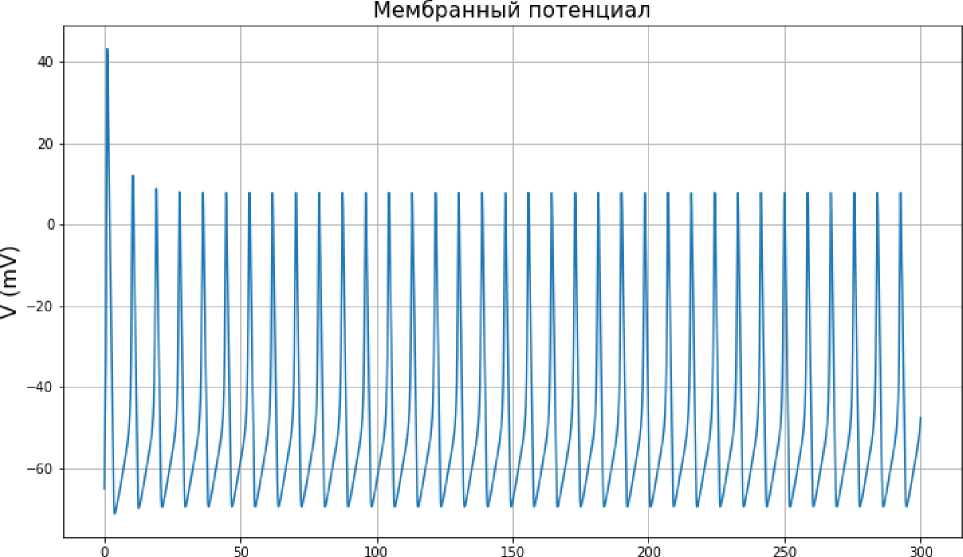
t (ms)

Рис. 7. Зависимость мембранного потенциала от времени по модели Ходжкина-Хаксли

при значении входного тока I _ext = 50 мА.

Воротные переменные

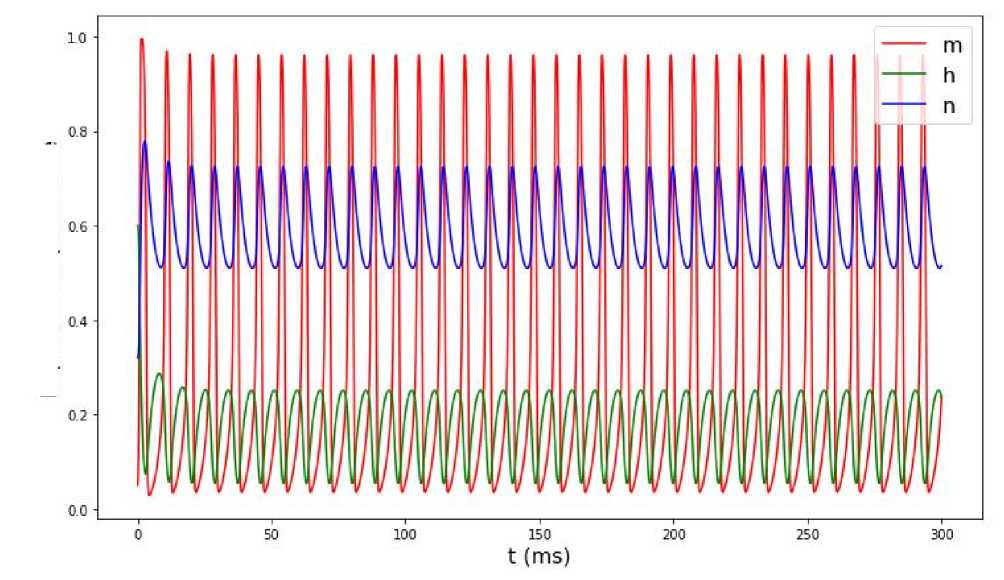
Рис. 8. Изменение воротных переменных с течением времени при значении входного тока I _ext = 50 мА.

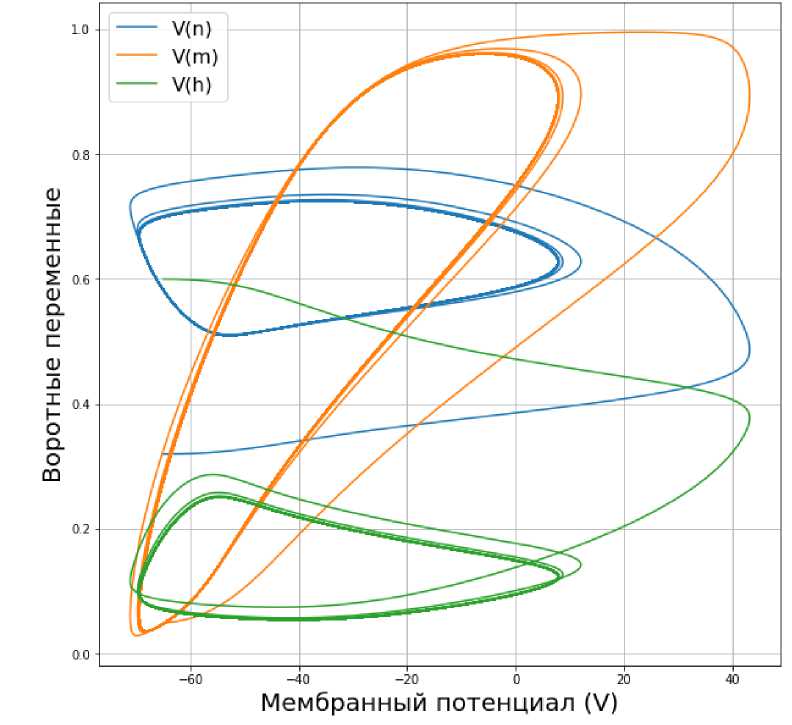
Рис. 9. Зависимость воротных переменных от мембранного потенциала V при значении входного тока Iext = 50 мА.

Заключение. Таким образом, меняя значения входного тока в модели Ходжкина-Хаксли, можно сделать вывод, что наиболее оптимальным значением, при котором возможно возбуждение нейрона и передача сигналов другим нейронам, является значение входного тока, равное 10 мА.