Численное моделирование обобщенной процедуры формирования индексов мягких решений
Автор: Гладких Анатолий Афанасьевич, Климов Роман Владимирович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии телекоммуникаций
Статья в выпуске: 2 т.11, 2013 года.
Бесплатный доступ
Предлагается универсальный метод вычисления индексов мягких решений (ИМР), необходимых для эффективной реализации процедуры мягкого декодирования помехоустойчивых кодов. Вводится показатель эффективности схемы формирования ИМР и определяются его асимптотические границы для различных видов сигналов. Граничные оценки аналитического моделирования синтезированных систем формирования ИМР выверяются результатами статистических испытаний соответствующих моделей.
Индексы мягких решений, численное моделирование
Короткий адрес: https://sciup.org/140191618
IDR: 140191618 | УДК: 621.391
Текст научной статьи Численное моделирование обобщенной процедуры формирования индексов мягких решений
Одной из особенностей передачи данных в мобильных мультисервисных сетях является обеспечение заданного уровня достоверности на участке радиоинтерфейса. Эта цель достигается путем использования различных методов, среди которых важное место принадлежит средствам помехоустойчивого кодирования [1-3]. Невзирая на значительное число исследований в этой предметной области, вопросы мягкого декодирования, в частности способы вычисления ИМР, остаются недостаточно изученными. Известны следующие способы формирования ИМР: на основе логарифмического отношения функций правдоподобия [1-2], на основе квантования модулируемого параметра сигнала на несколько уровней [1], на основе кортежа стираний в случае организации стирающего канала связи [3; 7-8]. При определении ИМР методом вычисления логарифма отношения функций правдоподобия приемником формируются нецелочисленные значения ИМР, что снижает производительность его процессора. Квантование сигналов по нескольким уровням требует решения системы неравенств, но существенным достоинством подобного подхода является возможность формирования целочисленных индексов. Третий способ требует специального построения решающего устройства для оценки сигналов с выделением некоторой зоны неопределенности (классический стирающий канал). Перечисленные методы противоречивы по своей сути, не пригодны для адаптивной выработки ИМР, не решают задачу формирования мягких решений при использовании сложных видов мо- дуляции и недвоичных преобразований данных. Целью работы является разработка унифицированного метода формирования целочисленных ИМР в системе мягкой обработки избыточных кодов.
Постановка задачи
Рассмотрим некоторое множество последовательностей конечной длины n , которые являются словами корректирующего кода. В мягком декодере каждый i -й бит принятого кодового вектора представляется в виде жесткого решения, сопровождающегося ИМР в виде некоторого л . Обозначая жесткие решения через «минус» для информационного нуля и через «плюс» для единицы, на выходе приемника получают кортеж данных • • • + Л - А+1 - А+2 + Л+З + Л + 4 • ■ • ’ который в последующем обрабатывается в мягком декодере, например итеративным методом.
Пусть {л} конечный алфавит множес
тва цело
численных индексов, для которых {А' /
^тт ■ ^тах ’
и для любого кодового вектора допустимо среди зафиксированных ИМР выделение
s
Обозначим для таких условий приема через Pos вероятность ошибочного декодирования кодовой комбинации. Очевидно, что
Pos^Pi-P^ Т^м (1)
z=О z=S+1
где Pj – вероятность появления таких значений ИМР, которые в алгоритме декодирования стираются, а р, – вероятность появления ошибок в этой же кодовой комбинации при наличии ровно i стираний, которые обеспечивают снижение вероятности ошибок, следовательно P;>PUX, Q = O;l...t/-1 = s).
Установим, что ^Oconst – вероятность ошибочного декодирования комбинации избыточного кода, когда всякий раз, используя принцип ранговой метрики, в принятом кодовом векторе формируется ровно I = S стираний. В этих условиях при реализации в процедуре декодирования требования ^;i для кодовых комбинаций длины n выполняется соотношение . Действительно, составим очевидное неравенство
Р^Р^Р^Р&Р.^Р.. (2)
/ = 0 /=5+1 / = 0 / = 5 + 1
НоЕ^+Ё^ = Ги p^p.+ ^p^p;, i=Q i=s-v\ /=0
тогда Р- > Р-+х и Pf^Pj <^Р^ • и, усили-/=о/=0
вая это неравенство, получаем
Р^Р^У.Р^Р'х-(3)
/=0/=5+1
Следовательно, PqS > Pticonst . Отсюда следует: во-первых, при декодировании комбинаций избыточного кода среди принятых символов отдельной комбинации, используя ранжированные ИМР, целесообразно выделить d — 1 стирание и исправить их выбранным способом; в таком случае, во-вторых, вероятность появления ошибочных символов среди нестертых позиций с высокими значениями ИМР должна быть минимальной.
Процедура формирования индексов
Широко распространенный способ формирование логарифмического отношения правдоподобия в модели гауссовского канала обеспечивает получение ИМР по правилу:
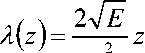
ст
где z – реализация сигнала; E – энергия сигнала на бит; <т2 – дисперсия условной плотности распределения вероятностей параметра z . Известно, что ст = No / 2 , где No – спектральная плотность гауссовского шума [4; 6]. Это обстоятельство приводит к изменениям динамического диапазона получаемых по данному методу ИМР, вызванных стохастическими вариациями соотношения «сигнал-шум». Следовательно, для различных условий обработки сигнала необходимо иметь некоторый набор линейных функций, формирующих ИМР при разных отношениях «сигнал-шум».
Справедливость этого вывода с определенным поправочным коэффициентом сохраняется и для каналов связи с замираниями различной природы. Таким образом, при изменениях ^о , но одинаковых z , возможно получение отличающихся друг от друга ИМР. Это снижает эффективность процедуры мягкого декодирования, особенно при использовании длинных кодов, когда одинаковые
ИМР могут соответствовать разным условиям обработки сигнала. Для оперативной актуализации значений X( z ) в ходе сеанса связи возникает необходимость постоянного мониторинга значений .
В целях совершенствования процедуры вычисления ИМР предлагается в решающей схеме приемника ввести широкий интервал стирания и всем значениям сигналов, принятых за пределами этой зоны в окрестностях математического ожидания случайной величины z , присваивать максимальную градацию надежности ^ max . Другие значения ^i < ^max необходимо формировать на основе линейной характеристики, как показано на рис. 1, где .
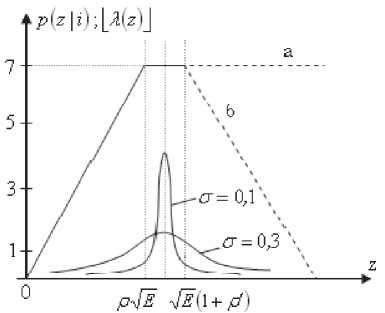
Рис. 1. Характеристики схемы прямого вычисления ИМР: а) для системы с АМ или системы широкополосных сигналов; б) для системы с ФМ-2
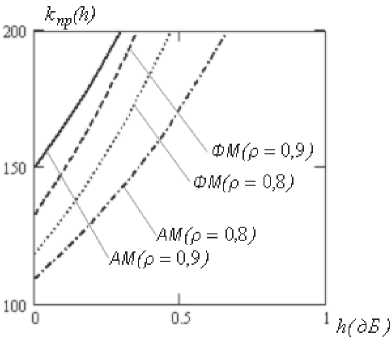
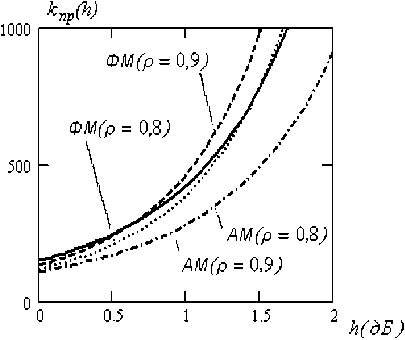
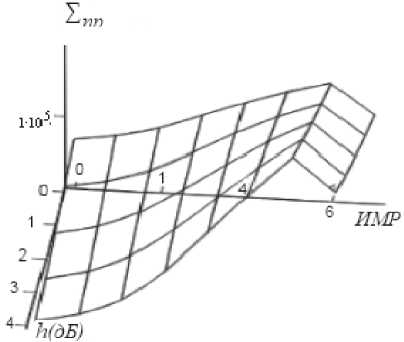
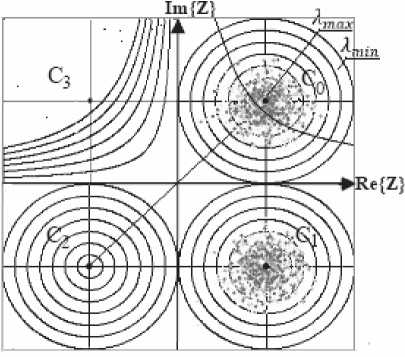
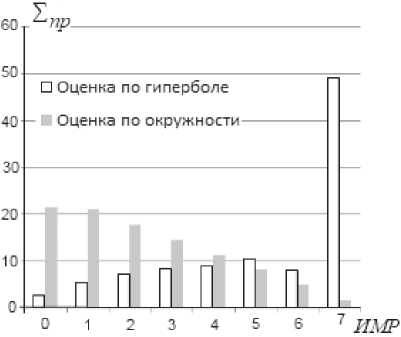
Для систем формирования ИМР с открытым интервалом (характеристика типа «а» на рис. 1) X формируется при условии Z > p^E. В силу особенностей фазовой модуляции рабочая характеристика носит закрытый характер (тип «б»), и ^ max формируется при выполнении условия р4Ё < z Общее для всех видов модуляции аналитическое выражение характеристик в пределах интервала стирания p имеет вид X.^- ^max PMxm где M– математическое ожидание модулируемого параметра. Указанный подход обеспечивает универсальность метода формирования ИМР и оставляет конструктору приемника свободу выбора для значения индекса с максимальным показателем. Важной особенностью метода является независимость показателей ИМР от знания статистических характеристик канала связи. Для системы с AM МИ„=|7Ё|, а для системы с ФМ-2 параметр КДравен номинальному значению фазы. Например, M.mX = ^/^ для «1» И Mлтй =-7tll для «О». В [8] в качестве критерия эффективности системы формирования ИМР был выбран коэффициент правдоподобия ^пр Рправ /Рош ’ где Р прав – вероятность совпадения оценки Д' с правильно принятыми символами, а Рош – вероятность ошибочной регистрации символов с оценкой . Этот показатель позволяет оценить потенциальные возможности проектируемой системы формирования ИМР. Например, для ^тах и ФМ-2 при Р = ^9 значение р оценивалось как г прав прав Вероятность ошибочной регистрации индекса ^тах при выбранном значении р определялось как 1,Ът/2 / _______ Рош = Jexp(-(z + ^/2)2/A^0)t/z /д/^Д . 0.45 л- / Аналогичным образом могут быть вычислены вероятностные оценки для системы с открытым интервалом. Тогда в качестве верхнего предела интегрирования предпочтительно использовать критерий «трех сигма» СУ . Выбирая соответствующие пределы интегрирования, возможно определение коэффициента правдоподобия для любого Л < ^-тах ■ Полученные результаты аналитического моделирования целесообразно использовать в качестве потенциальных оценок для различных кпр , степень приближения к которым указывает на эффективность аппаратных средств, формирующих ИМР. На рис. 2 представлены аналитические оценки k)n(Jp для индекса ^тах , двух значений и различных видов модуляции. Данные приведены для области низких значений параметра h. Заметно некоторое превосходство системы с открытым интервалом относительно системы с ФМ-2.Это свойство в последующем будет играть положительную роль при формировании ИМР в ходе применения сложных видов модуляции. Уменьшение параметра р приводит к снижению к пр W и, следовательно, к росту потерь в ходе мягкого декодирования принятого ко- дового вектора. Рис. 2. Поведение функции правдоподобия для различных видов модуляции и интервалов стирания в области низких отношений «сигнал-шум» С увеличением уровня сигнала значения потенциальных оценок к(/?) меняются в пользу системы с ДФМ. На рис. 3 представлен диапазон изменений отношения «сигнал-шум» от 0 дБ до 2 дБ. Заметно, что в правой части указанного интервал превосходство ФМ-2 проявляется более внятно,и это преимущество увеличивается при дальнейшем росте отношения «сигнал-шум». Рис. 3. Поведение функции правдоподобия для различных видов модуляции и интервалов стирания при увеличении параметра На рис. 4. приведены потенциальные оценки к QT) для других значений X-. В частности, показаны оценки для Л=5 и 4=3 при . Заметен существенный отрыв функции правдоподобия для индекса ^тах от приведенных оценок. Этот факт играет положительную роль при итеративных преобразованиях кодовых векторов независимо от типа кодека. А: Д) ' / Л = 7,р=0,9 ^Л=7,р=0,3 51= 5 Л= 3 0 °-5 ^к(дБ) Рис. 4. Поведение функции правдоподобия для сигналов ФМ-2 Очевидно, что при некотором значении р граница формирования индексов ^тах совпадает с интервалом для подобных оценок, формируемых по методу Витерби [2]. Однако при равномерном разделении пространства сигналов на зоны формирования индексов с использованием этого метода приемнику для поиска соответствующего принятому сигналу индекса необходимо решать систему линейных неравенств, что реализуется несколько сложнее предложенного прямого вычисления ИМР. Процедура формирования ИМР носит универсальный характер и из-за простоты своей реализации может быть успешно использована в процессорах современных цифровых систем обмена данными с ФМ-2, ФМ-4 и т.п. Результаты имитационного моделирования системы формирования индексов мягких решений Имитационное моделирование проводилось для системы с ФМ-2. В соответствии с правилом (3) интервал неопределенности разбивается на ^тт-{ целочисленных участков, которым от границы зоны стирания к жесткому порогу решающей схемы в порядке убывания номеров присваиваются соответствующие значения ИМР. Это означает, что в традиционной схеме со стиранием элементов символы, попавшие в зону неопределенности, должны интерпретироваться как стертые позиции, большинство из которых в обычной схеме стирающего канала связи оказались бы ложными стираниями [7]. В новых условиях символы с ИМР меньшими X также могут трактоваться как стирания, но они в отличие от классического стирающего канала связи будут иметь вполне определенные индексы надежности. В модели осуществлялась обработка 106 двоичных символов [6]. В ходе численного моделирования соответствующие накопители суммировали результаты испытаний в виде Ъ И ^ для каждой оценки, и на основе этого вычислялись частоты появления Рправ и Рош . С помощью этих данных формировались коэффициенты правдоподобия, которые затем сравнивались с соответствующими оценками аналитического моделирования. Формирование ИМР в модели осуществлялось в соответствии с выражением (4), в котором угловой коэффициент tg линейной зависимости определен первым сомножителем, а параметр z определен как . Условные операторы в моделирующем комплексе программ в системе MATLAB имели вид: elseif (0<=fi)&(fi elseif (stgr (2) elseif (-(pi) elseif (stgr (4) В таблице 1 приведены результаты, полученные при использовании аналитического моделирования и соответствующих им имитационных моделей. Результаты соответствуют . Таблица 1. Значения коэффициента правдоподобия Значение h , дБ p = 0,9 р = 0.8 Ан алит, модель Имитац. модель Аналит. модель Имитац. модель 0 131 132 121 118 0,46 228 226 197 196 0,97 445 446 379 374 1,54 1156 1098 851 842 2,22 3717 4022 2462 2677 3,01 117000 136700 10844 11850 Сравнение данных позволяет говорить об адекватности моделей. Превосходство показателей имитационного моделирования относительно аналогичных показателей аналитического моделирования после 1,5 дБ объясняется повышенной точностью имитационных моделей. Результаты статистических испытаний описанных систем выявили интересную особенность, которая заключалась в том, что итоговые оценки ^max не доминируют для интервала p = 0,9 и больше (см. рис. 5), но их к остается лучшим относительно других ^i ^ ^мах * Это указывает на верность разработанной концепции: использовать стирающий канал связи с широким интервалом стирания для выработки за его пределами ИМР с высокими показателями их достоверности. Рис. 5. Сравнения суммарных оценок при /7 = 0,9 Рис. 6. Зависимость коэффициента правдоподобия от соотношения «сигнал-шум» при равномерном разбиении пространства регистрации сигналов (1) и получения ИМР на основе стирающего канала (2) Одновременно с этим показано, что значения к (/z) в области больших отношений «сигнал-шум» для стирающего канала связи превосходят аналогичные данные для системы с равномерным разбиением пространства регистрации сигнала на зоны формирования целочисленных ИМР (см. рис. 6). Формирование индексов мягких решенийвсистеме сложныхсигналов Одним из недостатков современных систем с OFDM является невозможность избирательной адаптации пропускной способности элементарных каналов к частотным характеристикам всего частотного канала [1]. Решение этой проблемы лежит на пути применения мягких декодеров, позволяющих гибко использовать полученную приемником информацию из отдельных частотных каналов. Другим направлением применения мягких методов в ходе обработки сложных сигналов являются системы с иерархической модуляцией [4]. Предложенный метод формирования ИМР в силу своей универсальности пригоден и в этих случаях. Рассмотрим метод формирования мягких решений на примере КАМ-4. На рис. 7 показано созвездие подобных сигналов. Для применения метода необходимо использовать систему концентрических окружностей, которые на комплексной плоскости определят рабочую точку z. Наиболее критическими расстояниями между точками созвездия являются интервалы примыкающих квадрантов. Рис.7. Альтернативные принципы разбиения созвездия КАМ-4 на зоны для получения ИМР Недостатком подобного разбиения является: во-первых, неопределенное пространство сигналов в области начала координат, которое условно можно принять за ^т т 5 во-вторых, завышенное количество низких ИМР из-за формирования подобных оценок в областях, не примыкающих к соседним квадрантам. На рис. 7 (второй квадрант) показан принцип устранения последнего недостатка за счет применения гиперболических границ вместо концентрических окружностей. Но применение подобного подхода возвращает к решению системы линейных неравенств для поиска X, , что противоречит целевой установке. Тогда, принимая за опорные точки номинальные значения k^i } CoX\vXY« КАМ-сигнала и получив комплексное значение сигнала zk ’ приемник выполняет проверку его принадлежности к окружности радиуса iy. |^-q| = //- В этом случае /' = z ’ используя (4), приемник формирует Aj ? при этом зона неопределенности в области начала координат принимается за . Для рационального вычисления индексов ^max целесообразно использовать еще одну границу, которую назначают в виде дробно-линейной функции вида ax + b _ V =----- при c ^ 0. ' ex+ 5 Выражение (5) приводится к уравнению равносторонней гиперболы с переносом начала координат в точку пересечения окружности 7? — ^max с прямыми _v = |,y| . Асимптоты такой равносторонней гиперболы параллельны осям комплексной плоскости. На рис. 8 представлен выигрыш при формировании ИМР по правилу концентрических окружностей и при комплексном использовании этого правила с правилом равносторонней гиперболы. Рис. 8. Сравнительные характеристики правил формирования ИМР в системе КАМ-сигналов Принцип вычисления ИМР в последнем случае несколько усложняется, но это повышает эффективность работы декодера при использовании сложных видов модуляции. Обсуждение результатов В условиях стремительного роста трафика данных относительно иных информационных потоков применение мягких декодеров позволяет решить задачи повышения достоверности данных достаточно эффективно без существенного роста сложности приемных устройств. Предложенная процедура формирования ИМР носит универсальный характер и из-за простоты своей реализации может быть успешно использована в процессорах современных цифровых сис- тем обмена данными, использующих принципы радиоинтерфейса. Свободный выбор диапазона изменения целочисленных ИМР позволяет конструктору приемника эффективно решать задачу сложности реализации мягкого декодера. Важное практическое значение имеет открывающаяся возможность адаптивного изменения интервала стирания путем смены параметра р для выработки ИМР в условиях изменения уровня сигнала. При этом поток оценок 2ц на некотором зачетном отрезке данных может явиться индикатором для смены выбранных параметров. Вслучае исправлениядекодером помехоустойчивого кода стертых позиций решается вопрос об идентификации ложных стираний и назначении приоритетов при перестановочном декодировании или декодировании на основе эквивалентных кодов. Внедрение широкополосных систем обмена данными, применение в них сложных видов модуляции и недвоичных кодовых конструкций открывает новые возможности для мягкого декодирования таких кодов и решения важной задачи снижения сложности реализации декодеров недвоичных кодов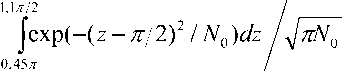
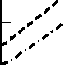
Список литературы Численное моделирование обобщенной процедуры формирования индексов мягких решений
- Скляр Б. Цифровая связь. М.: Радио и связь, 2000. -800 с
- Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. М.: Техносфера, 2005. -320 с
- Гладких А.А. Основы теории мягкого декодирования избыточных кодов в стирающем канале связи. Ульяновск: Изд. УлГТУ, 2010. -379 с
- Волков Л.Н., Немировский М.С., Шинаков Ю.С. Системы цифровой радиосвязи: базовые методы и характеристики. М.: Эко-Трендз, 2005. -392 с
- Возенкрафт Дж., Джекобс И. Теоретические основы техники связи. М.: Мир, 1969. -640 с
- Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. М.: Радио и связь, 1991. -410 с
- Шувалов В.П. Прием сигналов с оценкой их качества. М.: Связь. 1979. -240 с
- Гладких А.А., Мансуров А.И, Черторийский С.Ю. Статистическая оценка индексов достоверности символов, формируемых в системе с мягким декодированием//ИКТ. Т.6, №1, 2008. -С. 39-43


