Численное моделирование обтекания профиля NaCa-0012 в струйно-перфорированных границах

Созданию аэродинамических труб сопутствовало возникновение проблемы влияния стенок рабочей части АДТ, в которой устанавливается испытываемая модель. В результате проведения испытаний получаемые экспериментальные величины отличаются от результатов, соответствующих обтеканию безграничным потоком. Именно поэтому вместе с появлением аэродинамических установок возник вопрос о разработке теоретических и экспериментальных методов корректировки получаемых данных, исключающих индукцию границ.

Проблема, влияния стенок рабочей части на. обтекание тестовых моделей возникает в случае невыполнения определенных законов по границе рабочей части АДТ. Таким образом, если рабочая часть имеет жесткие стенки, то нормальная к поверхности стенок составляющая скорости должна равняться нулю; если же рабочая часть представляет собой свободную струю, то на поверхности струи давление должно быть постоянным и равным

давлению в камере, отделяющей рабочую частв от окружающей атмосферы. Влияние этих граничных условий приводит к тому, что течение около модели, помещенной в рабочую частв АДТ, оказывается отличным от течения, получаемого при обтекании того же тела безграничным потоком. Сплошные стенки ограничивают возможноств свободного отклонения линий тока в месте расположения модели. В итоге, если течение, например, дозвуковое, то это приведет к увеличению осевой скорости в области модели в сравнении с режимной скороствю потока [1]. Особенно актуальным вопрос уменьшения индукции стенок рабочей части аэродинамической трубы стал при создании околозвуковых аэродинамических установок, когда использование непроницаемых стенок стало неприемлемым вследствие явления запирания рабочей части трубы в месте расположения модели.

Одно из первых решений данной проблемы было предложено в 1948 г. группой советских ученых под руководством С. А. Христиановича. Оно представляло собой использование перфорированных панелей вместо сплошных стенок рабочей части АДТ. Благодаря данному решению был осуществлен переход через скорость звука, что позволило получить поток с числом Маха, большим единицы, и в некоторой степени уменьшить влияние границ потока [2]. Однако использование перфорированных границ привело к усложнению методики проведения эксперимента [3]. В частности, возникла проблема учета влияния перфорированных стенок рабочей части АДТ на аэродинамические характеристики испытываемой модели. Кроме этого, использование перфорированных панелей с постоянным коэффициентом проницаемости не позволяет одновременно устранить влияние стенок на все основные аэродинамические характеристики.

Поиски альтернативных способов решения проблемы индукции границ потока привели к развитию концепции «адаптивных» границ. При использовании данного метода граничные условия могут изменяться в темпе эксперимента. Корректная адаптация граничного условия может устранить влияние стенок или, по крайней мере, значительно снизить её [4-6]. Основная идея, на которой базируется данный подход, основана на общеизвестном свойстве течений несжимаемой жидкости: задание на границе области нормальной компоненты скорости полностью определяет течение внутри нее. Если распределение нормальной компоненты скорости вдоль контрольной поверхности около стенки совпадает с аналогичным распределением в случае безграничного потока, то влияние стенок будет устранено. К АДТ с адаптивными границами можно отнести установки с гибкими стенками и их модификации; стенки с секционно-регулируемой проницаемостью, где заданное значение нормальной составляющей скорости достигается путем изменения просвета перфорационных отверстий или щелей; АДТ с секционированной камерой давления. Во всех случаях использования адаптивных границ удается приблизить характер течения к соответствующему обтеканию безграничным потоком и, возможно, устранить качественные отличия обтекания модели в АДТ и в полете, но это не является окончательным решением проблемы индукции. Более того, очевидно, что усложнение граничных условий создает серьезные, а порой и непреодолимые, трудности при попытке определить остаточную индукцию. Использование адаптивных границ в промышленных АДТ большого размера не вошло в практику аэродинамических исследований еще и по причине дороговизны испытаний, поскольку для получения одной экспериментальной точки требуется выполнить длительную итерационную процедуру.

Дальнейшие поисковые исследования более эффективных методов уменьшения индукции границ привели к развитию альтернативных концепций малоиндукционных АДТ. Одна из таких концепций - применение струйных границ - была предложена В.М. Нейланд и В. Я. Вейландом в 1984 г [7]. Авторами было показано, что новый тип границ обладает рядом преимуществ по сравнению с традиционными проницаемыми и позволяет при правильном выборе параметров пристеночных струй практически устранить влияние стенок на все основные аэродинамические характеристики модели.

Согласно расчетным оценкам и полученным В.М. Вейланд и В. Я. Вейландом экспериментальным данным, оптимальные струи вблизи свободных границ должны иметь ско- ростной напор, больший, чем у набегающего потока, а в случае жестких стенок - всегда меньший, чем у основного течения в АДТ.

В.М. Нейланд был получен алгоритм оптимизации струй [8], в результате которого практически устранялось влияние стенок. Остаточная индукция оказалась значительно меньшей, чем в случае оптимальной перфорации при приблизительно одинаковых условиях. Помимо основного преимущества, струйные границы обладают еще рядом свойств, таких как уменьшение уровня шума, по сравнению с перфорированными стенками, возможностью термоизоляции криогенного потока и т.д. Однако данный подход не получил широкого применения из-за технологической сложности реализации управляемых струйных установок в промышленных аэродинамических трубах.

Действенным способом для уменьшения индукции границ оказался метод, основанный на использовании управляемого пограничного слоя [9]. Управляемый пограничный слой на жесткой стенке рабочей части может быть рассмотрен как аналог струйной границы, поскольку пограничный слой является аналогом пристеночной струи с меньшим (по сравнению с основным потоком) скоростным напором. Данный метод оказался достаточно эффективным и технически легко реализуемым. Практическая реализация нового подхода была осуществлена на базе аэродинамической трубы трансзвуковых и сверхзвуковых скоростей Т-112 ЦАГИ [10].

Эффективность применения управляемого пограничного слоя на гладких стенках АДТ для уменьшения индукции границ потока была показана экспериментально с геометрически подобными моделями [11]. Однако в случае, когда испытываемые модели перераз-мерены, толщины пограничного слоя оказывается недостаточной для устранения индукционных возмущений. С целью преодоления возникшей проблемы опробован новый вид граничных условий, которые представляли собой комбинацию управляемого пограничного слоя и перфорированных стенок. С данным граничным условием был проведен ряд экспериментальных работ на базе аэродинамической трубы трансзвуковых и сверхзвуковых скоростей Т-112 ЦАГИ, результаты данных исследований продемонстрировали положительный эффект использования нового граничного условия [12, 13].

2.    Программа и метод расчета

Целью данного численного исследования было подтвердить эффективность использования комбинированного струйно-перфорированного граничного условия для уменьшения индукции границ, а также подобрать комбинацию параметров пограничного слоя и коэффициента проницаемости перфорированной стенки, при которой влияние стенок рабочей части АДТ будет минимально.

Моделирование контролируемого пограничного слоя на входе в тестовую секцию осуществлялось с помощью задания профиля продольной составляющей скорости:

u(y) = tanh((y + ^h)k) • (- tanh((y + 2)k - kh)) • u^,

где h — высота рабочей части; u^ - скорость невозмущенного потока; k - безразмерный коэффициент, определяющий профиль скорости у стенок.

Моделирование перфорированных панелей осуществлялось с помощью задания на стенке граничного условия для перфорированной стенки, которое обычно представляется как линейная связь двух компонент «возмущенной» скорости (так называемое граничное условие типа Дарси):

u + v/R = 0, где u и v - безразмерные компоненты возмущенной скорости, a R - параметр проницаемости.

Для анализа корректности выбранных параметров граничного условия необходимыми являются результаты расчета обтекания тестовой модели в условиях безграничного потока, которые в дальнейшем служат ориентиром при выборе и оптимизации параметров границ.

В настоящей работе численное исследование проводилось с помощью кода EWT-TsAGI, который используется в ЦАРИ с 1996 года. Данный подход хорошо описан в работах [14, 15]. Используемый код позволяет решать стационарные (RANS) и нестационарные (URANS) уравнения Навье-Стокса с использованием усреднения по Рейнольдсу. Все результаты, представленные здесь, основаны на подходе RANS. Для замыкания системы уравнений Рейнольдса используется модель турбулентности SST [16].

3.    Численное моделирование обтекания профиля NACA-0012

При валидации нового метода важным аспектом является возможность использования базы данных достоверных результатов обтекания модели, как, например, для профиля NACA0012. В рамках численного исследования в данной работе характеристики тестовой модели были получены при моделировании обтекания безграничным потоком, в жестких стенках, в стенках с граничным условием типа Дарси и в комбинированных струйно-перфорированных границах. В качестве экспериментальных данных для валидации результатов численного моделирования были выбраны данные, представленные в работе [17]. Геометрические параметры моделируемой рабочей части также были взяты из данной работы [17] (загромождение рабочей части составило порядка 4%). Число Маха составило 0.799, угол атаки варьировался от 0° до 5° с шагом в 1°. Сравнение расчетных и экспериментальных данных показывает, что в некоторых областях на поверхности профиля совпадение кривых распределения давления практически полное (рис. 1).

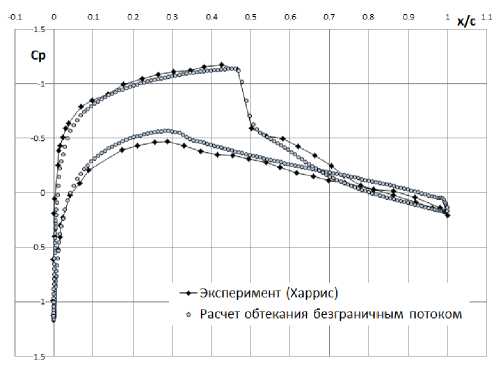
Рис. 1. Сравнение эпюр давления по профилю NACA0012 при М = 0.799, a = 2.26°

На первом этапе научной работы было проведено численное исследование для нахождения оптимального параметра проницаемости для разных углов атаки. Основываясь на том, что при однородном граничном условии на проницаемой границе с параметром Дарси, стремящимся к бесконечности, стенка может быть рассмотрена как свободная граница, а при R = 0 является жесткой стенкой, были рассмотрены следующие случаи для коэффициента Дарси: от 0.01 до 0.04 с шагом 0.005; от 0.05 до 0.1 с шагом 0.01; 0.12; 0.15; 0.2; 0.3; 0.4. В результате данной поисковой работы были выбраны коэффициенты проницаемости для дальнейшей корректировки граничного условия с помощью толщины пограничного слоя. Для примера на рис. 2 представлены полученные результаты коэффициента распределения давления для угла атаки 4°. Также на рис. 3 представлены значения коэффициента подъемной силы при обтекании безграничным потоком и значения коэффициента подъемной силы для разных параметров Дарси. Точка пересечения кривых соответствует параметру Дарси, при котором достигается наименьшее расхождение для коэффициента подъемной силы при обтекании модели безграничным потоком и в перфорированных границах. Таким образом, для угла атаки 4° наименьшее влияние стенок рабочей части АДТ достигается при параметре Дарен R = 0.03.

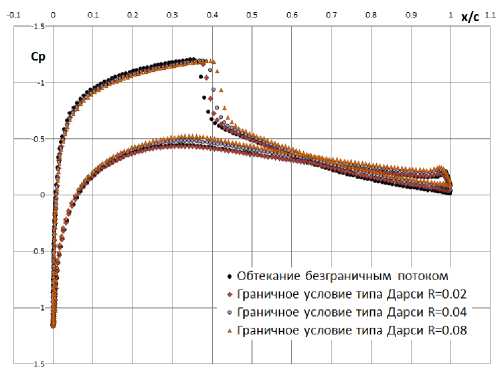
Рис. 2. Эпюры давления по профилю NACA0012 при М = 0.799, а = 4°

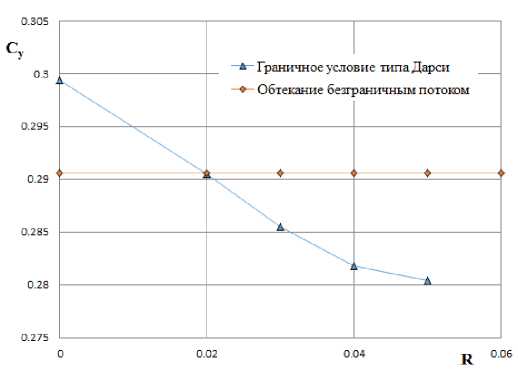
коэффициента, подъемной силы от коэффициента, проницаемости при

Рис. 3. Зависимость М = 0.799, а = 4°

Для анализа. эффективности использования комбинированных струйноперфорированных границ были рассмотрены данные конкретные коэффициенты проницаемости для каждого угла, атаки.

Моделирование управляемого пограничного слоя на входе в рабочую часть осуществлялось с помощью задания профиля продольной компоненты скорости [8]. Исследования эффективности использования комбинированных границ были проведены для следующих значений безразмерного коэффициента к, определяющего профиль скорости у стенок по формуле (1): 0, 10, 15, 17, 19, 20, 23, 25, 25.5, 26, 27, 29, 30, 40.

На рис. 4 представлены распределения числа. Маха, при обтекании профиля на. угле атаки 4° безграничным потоком, в жестких стенках со свободно нарастающим пограничным слоем, в условиях стенки с граничным условием Дарси, а. также при использовании комбинированных струйно-перфорированных границ. На представленных рисунках хорошо видно, как выбор граничного условия влияет на. картину обтекания, в частности по изменениям поведения изолиний числа. Маха.

В результате использование комбинированных границ при обтекании профиля позволило значительно снизить расхождение для интегральных характеристик, как, например, для представленных в табл. 1 коэффициента, подъемной силы и в табл. 2 момента, тангажа.

Таким образом, для коэффициента подъемной силы на угле атаки 2° расхождение между данными в перфорированных границах и при безграничном обтекании составило порядка 0.001, а использование комбинированных струйно-перфорированных границ позволило снизить до 0.0001, для коэффициента момента тангажа данное расхождение удалось снизить с 0.005 при моделировании обтекания профиля в стенках с граничным условием типа Дарси до 0.003 в комбинированных струйно-перфорированных границах.

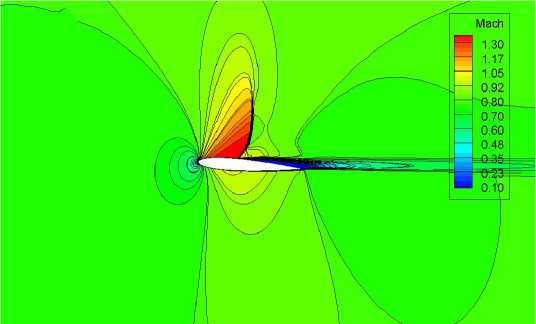
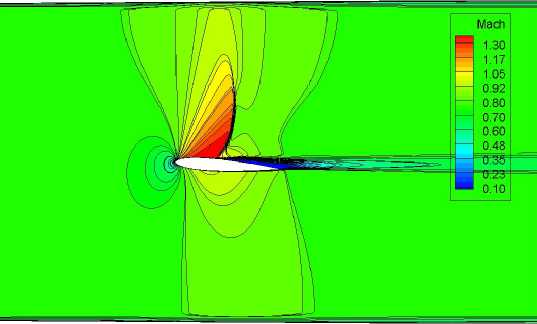
Обтекание безграничным потоком

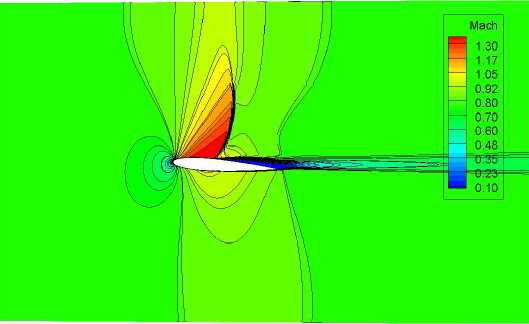
В жестких стенках

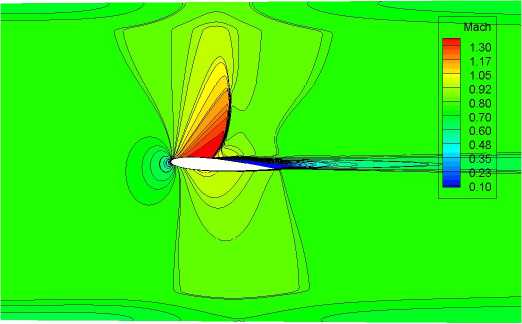
В стенках с граничным условием типа Дарси

В комбинированных струйно-перфорированных границах

Рис. 4. Распределение числа Маха при обтекании профиля NACA0012 а = 4°

Таблица 1

Сравнение результатов для коэффициента подъемной силы при разных граничных условиях

	а = Г	а = 2°	а = 3°	а = 4°
Безграничный поток	0.16973	0.261788	0.284	0.290588
Перфорация	R = 0.07	R = 0.035	R = 0.03	R = 0.03
	0.167686	0.261684	0.283	0.290652
Комбинированные границы	R = 0.07 К =15	R = 0.035 К = 25	R = 0.03 К = 27	R = 0.03 К = 25.5
	0.170192	0.261684	0.283	0.290652

Сравнение эпюр давления по профилю на разных углах атаки также демонстрирует положительный эффект использования комбинированных границ. Получена хорошая сходимость результатов при обтекании модели безграничным потоком, а также в условиях комбинации перфорированных границ и управляемого пограничного слоя на них (рис. 5).

Таблица 2

Сравнение результатов для коэффициента момента тангажа при разных граничных условиях

	а = 1°	а = 2°	а = 3°	а = 4°
Безграничный поток	0.045413	0.062128	0.054019	0.044432
Перфорация	R = 0.07	R = 0.035	R = 0.03	R = 0.03
	0.007155	0.005093	0.004559	0.003378
Комбинированные границы	R = 0.07 К = 30	R = 0.035 К = 27	R = 0.03 К = 27	R = 0.03 К = 30
	0.002583	0.00301	0.003775	0.00246

4.    Заключение

В данной научно-исследовательской работе приводится описание цикла расчетных исследований, направленных на продолжение анализа нового методического подхода к проблеме уменьшения индукции границ потока в рабочей части аэродинамической трубы при трансзвуковых скоростях потока. На примере обтекания модели профиля NACA-0012 был проведен сравнительный анализ полученных численным методом аэродинамических характеристик модели в разных граничных условиях, включая комбинированные струйно- перфорированные границы. Получена хорошая сходимость для эпюр давления на разных углах атаки, а также удалось существенно снизить расхождение между значениями коэффициентов подъемной силы и момента тангажа, соответствующих обтеканию безграничным потоком и в комбинированных границ. Для полученных значений коэффициента подъемной силы при моделировании обтекания в перфорированных и комбинированных границах расхождение с обтеканием безграничным потоком удалось снизить на порядок.

Стоит отметить, что проведенный анализ был осуществлен для случая двумерного обтекания модели профиля NACA-0012, поэтому для дальнейшего развития методики использования комбинированных границ планируется проведение численных исследований в случае трехмерного обтекания.

Авторы выражают глубокую благодарность А. И. Иванову за полезные обсуждения и замечания.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-38-00735.