Численное моделирование полных сечений рассеяния очень холодных нейтронов на сплошном бесконечном круговом цилиндре

Введение ¹

Макроскопические свойства2 материалов сильно зависят от элементов3 структуры4 с характерными размерами от единиц до сотен нанометров. Введение наноразмерных наполнителей

ВЕСТНИК 2014. ВЫПУСК 4

в полимерную матрицу нанокомпозитов позволяет создавать многофункциональные материалы с высоким модулем упругости, большой электропроводностью и теплопроводностью [1]. Они также обладают повышенной прочностью и эластичностью. При создании новых материалов с улучшенными свойствами в качестве наполнителя довольно часто используются многослойные углеродные нанотрубки (МУНТ). Перечисленные выше макроскопические свойства зависят от параметров этих трубок и их распределения в полимерной матрице нанокомпозита. Для определения параметров МУНТ широко используется электронная микроскопия, рентгеновская дифракция и малоугловое рассеяние рентгеновских лучей. Эти методы исследования структуры композиционных материалов наряду с неоспоримыми достоинствами обладают и существенными недостатками. Так, например, электронная микроскопия требует сложной предварительной подготовки образца толщиной от 10-2 до 10 мкм. С помощью рентгеновских лучей нельзя исследовать магнитные структуры. Из-за сильного поглощения рентгеновских лучей и электронных пучков крайне затруднительно применение этих методик при увеличении толщины исследуемых образцов.

Развитие нейтронных методов исследования вещества, использующих высокопоточные пучки нейтронов, привело к созданию уникальных установок на импульсных и стационарных реакторах, таких, как трехкристальные спектрометры, спектрометры обратного рассеяния, малоугловые дифрактометры с высоким разрешением по переданному импульсу. Создание и функционирование подобных приборов требует больших затрат, высокого уровня математического обеспечения. В то же время использование для исследования нейтронов очень низких энергий значительно упрощает экспериментальные установки, хотя и усложняет теоретическое обоснование.

Очень холодные нейтроны (ОХН) - это нейтроны, двигающиеся в вакууме c энергий 5-10-7 < en < 5^ 10 7 (длина волны де Бройля 1 < Xn < 100 нм). При таких энергиях нейтроны эффективно и на большие углы рассеиваются на элементах структуры с характерными размерами от единиц до сотен нанометров. При взаимодействии такой волны с препятствием меняется состояние нейтронов, состояние же мишени не изменяется, так как энергия ОХН много меньше энергии химических связей между атомами и энергии элементарных возбуждений. В этом случае процесс взаимодействия нейтронов с исследуемым образцом сводится к отражению, преломлению и дифракции нейтронной волны. Свойства очень холодных нейтронов определяются оптическим ядерным потенциалом [2-4]:

V ( r ) = (2 п Й ²/ m n ) b р ( r ). (1)

Здесь r - текущая координата нейтрона; Й - постоянная Планка; m n - масса нейтрона; р ( г ) - плотность частиц исследуемого образца. Константа b - это усреднённое значение когерентных амплитуд рассеяния на связанных ядрах рассеивающей системы. Квадрат показателя преломления, полностью описывающий оптические свойства такой среды, определяется выражением:

m ² = 1 - V / E , (2) где E - энергия нейтрона, падающего из вакуума. Отметим также, что оптический ядерный потенциал V ( r ) - это макроскопическая величина. Он зависит только от термодинамического состояния системы и не зависит от мгновенных положений атомов, из которых состоит рассеивающая система. Мы заменили традиционное обозначение коэффициента преломления n на символ m , для того чтобы сохранить обычные обозначения и индексы при записи решения уравнения Бесселя (функций J_n и функций н П ¹’).

В газах, жидкостях и аморфных твёрдых телах V ( r ) - это константа. Значит, и показатель преломления зависит только от скорости нейтронов, падающих из вакуума на исследуемый образец 5 <  v n < 100 м/с. Более подробно смотри теоретические исследования, выполненные в работах [5-9].

В этих работах было подробно обосновано использование простого метода ослабления ОХН, позволяющего получить информацию о наноструктуре исследуемых материалов при пропускании пучка нейтронов через образец, и исследовании зависимостей полных сечений упругого некогерентного рассеяния ОХН от длины волны нейтрона.

Цель настоящей работы - рассмотреть и сравнить поведение полных сечений упругого рассеяния ОХН, построенных на основе решения задачи рассеяния - точного решения скалярного уравнения Шрёдингера и первого бор-новского приближения для ОХН. Углеродные нанотрубки мы будем описывать как цилиндры, длина которых во много раз превосходит радиус R . Оптический ядерный потенциал V ( r ) - это константа, равная U .

Теоретические основы метода рассеяния ОХН

Фундаментальная величина в нейтронной оптике - когерентная волна, ^ ( r ). Она обеспе

чивает полное описание всех когерентных упругих процессов рассеяния. В области достаточно больших расстояний r между рассеивателем и точкой наблюдения она удовлетворяет одноча

циям и граничные условия на поверхности цилиндра, получим для падающей волны V i , внутренней волны v ₁ и рассеянной волны v s выражения: to

V i = Е ( - i ) n J ( kr sin Z ) e - ikcos ^Z z ,    (7)

n =-to

стичному скалярному уравнению Шрёдингера [3]:

[ ( h ²/2 m n ) А + U ] v M = E y ( r ).    (3)

В уравнении (3) h - это постоянная Планка; m n - масса нейтрона; А - оператор Лапласа; U - оптический ядерный потенциал; E - энергия падающего нейтрона. Отметим, что потенциал U и, следовательно, решение ^ ( r ) - это

V i = Е a n ( - i ) J ( kr^m ² - cos² Z ) e - k ^{cos Z} z , (8) n = -to

V s ^{( r} ф , ^z ) =

= £ ( - i ) ⁿ ( b_n /2) H^(kr sin Z ) e¹ ” ” - ^{k cos Z z} . (9) n =-to

макроскопические величины.

Выбор решений уравнения (3) диктуется видом симметрии, которая имеется в задаче. Нанотрубки лучше всего описывать, как цилиндры, длина которых во много раз превосходит диаметр. Поэтому построим точное решение задачи рассеяния на бесконечно длинном круговом цилиндре.

Итак, однородная плоская волна V i = = exp( ik e i x ), распространяющаяся в направлении вектора e i = - sin Z e x - cos Z e z , падает на бесконечно длинный прямой круговой цилиндр радиуса R . Ось цилиндра совпадает с осью OZ прямоугольной системы координат ( x , y , z ). Вектор e i лежит в плоскости ( x , z ), образуя с осью z угол Z . Волновой вектор рассеянной волны k _s лежит в плоскости, проходящей через ось z .

Запишем уравнение (3) в цилиндрической системе координат ( r , ф , z ):

В формуле (9) множитель 1/2 введён для удобства. Так как при упругом рассеянии число частиц сохраняется (квадрат амплитуды сходящейся волны равен квадрату амплитуды расходящейся волны), то мы можем записать:

11 + b n ^ = 1, b = e ²^ - 1, b = b n . (10)

Здесь 5 _n - фазовый сдвиг. Амплитуда рассеяния f ( ф ) определяется из соотношения:

u s = V i ⁺ V s

^^^^^^в

ikr sin Z e - xk- ) ^ f ( ф ) ^e , r

f ( ф ) =

2 n k sin Z

to

Е ( - 1) n ( b n /2) e

Ьф) - i n /4 - ik cos Z z

. (12)

n =-to

Коэффициенты a n и b_n находятся из граничных условий:

V i ^{( r} ) + V s ^{( R} ) = V t ^{( R} ),

[ д / д r ( r • V i ( r ) + r • V s ( r ))] r = r = [ д / д r ( r • V t ( r ))] r = r

Используя тождество

J n - 1 ( x ) H^¹ ( x ) - J n ( x ) H n - 1 ( x ) = 2/ nix ,   (13)

1 д f д --I r— r д r I д r

+

± д ²    д ² k ₂

r² дф ²⁺ дz^{2 +}

V ( r, Ф ,z ) = 0 . ⁽⁴⁾

Однозначные по ф решения уравнения (4) имеют вид:

V n ( r , Ф , z ) = Z n ( р ) e i ^^{+ ihz} , n = 0,1,2,... (5) где р = r V k ² - h² , а Z_n - решение уравнения Бесселя:

Рг I Pp Z n 1⁺ ( р ² - n ²) Z n = 0. (6) d p ^ d р )

Линейно-независимыми решениями уравнения (6) являются функции Бесселя первого и второго рода J_n и Y_n с целочисленными значениями индекса n . Величина константы разделения h определяется видом падающего поля и необходимостью выполнения граничных условий на поверхности рассматриваемого цилиндра (нанотрубки).

Используя разложение по собственным функ-

можно получить:

a = J n ( x ) H14 x ) - J n ( x ) H n **' ( x ) = n    m * J n ( x ') Н П ^!)( x ) - J n ( x ') H n ¹»' ( x )

_            2 / n ix

" m*Jn(x')H^(x)- Jn(x')H^(x), b = m‘Jn (x') Jn (x) - Jn (x')Jn (x)

ⁿ m * J n ( x ') H^( x ) - J n ( x ') H^ ( x )

В формулах (13), (14) и (15) введены обозначения x' = kR^m ² - cos² Z , x = kR sin Z ; штрих, стоящий сверху около функций J_n и H _n ⁽¹⁾ , означает дифференцирование этих функций по их аргументам - либо x , либо x ' ; m* = x ' / x = m ² - cos² Z / sin Z , m ² = 1 - U / E -

показатель преломления препятствия.

Вычислив коэффициенты b_n , можно определить дифференциальное сечение рассеяния на

единицу длины цилиндра:

ВЕСТНИК 2014. ВЫПУСК 4

d ^ sc =1 f Г N =

2 π k sin ζ

∞

| b0 + 2^bn cos пф |2 dф n=1

Выполнив интегрирование дифференциаль-

ВЕСТНИК 2014. ВЫПУСК 4

ного сечения рассеяния на единицу длины цилиндра d o s, по углу ф , мы получим следующую формулу для вычисления полного сечения рассеяния единицей длины прямого кругового цилиндра:                     „     \

- =         Ub 0^{| 2} + 2 ^ 1 b n 1² | .    (17)

k sin Z к 1       )

Рассмотрим задачу рассеяния ОХН бесконечным длинным круговым цилиндром радиуса R при нормальном к оси цилиндра падении ОХН п

( Z = —) в первом борновском приближении [10].

Потенциальная энергия – оптический ядерный потенциал – U рассматривается как возмущение. Волновую функцию мы будем искать в виде ф = = ф ₀ + ф ₁ , где функция ф ₀ = exp( i kr ) - соответствует падающей частице. В цилиндрической системе координат ( р , ф , z ) расходящаяся волна на больших расстояниях от оси имеет асимптотическое выражение функции Ганкеля первого рода [10], и поправка ф ₁ к волновой функции ф ₀ на больших расстояниях от оси цилиндра R ₀

будет:

m ф =-  n5

¹      2 n h h

j U ( p , z ) e^l kr • i n H 0(1) ( k p ) р А р А ф =

= f_B ( ф )

e ikR 0 R

.

Здесь m_n – масса нейтрона; отсюда амплитуда рассеяния f_B ( ф ):

f« ( ^ ) = - mS Й

π i e 4

Й ²                         ,,.,.

,     [---- (4 n Nb_c ) e ^qp p d p d ф =

2 n k 2 m_n

= -\ 2 4 ^ ⁽ Nb c ) e ' ⁴ ■ ^J'^qR)"R 2 , ²’ [см^1/2]   (19)

kqR где q = ki - ks - вектор рассеяния, q = 2k sin ф / 2.

Сделав в (19) замену переменных 9 = п - ф, получим формулу для вычисления дифференциального сечения упругого рассеяния ОХН d^B = 2п (Nb )2 ( 2J,(2ksin(9 /2)R) A 2x d9   kVc к   2 kR sin 9/2   i

Обсуждение результатов численного моделирования

На рис. 1–4 приведены диаграммы рассеяния, вычисленные по формулам, полученным на основе решения уравнения Шрёдингера методом разделения переменных, и по формулам борнов-ского приближения. Для вычисления коэффициентов b_n в (17) использовались алгоритмы, изложенные в работах [13–14]. Время вычисления можно существенно сократить, если воспользоваться методами волновой теории катастроф [15– 22]. На графиках по вертикальной оси отложены полные сечения рассеяния в логарифмическом масштабе (одно деление – 10 единиц), по горизонтальной оси – скорость нейтронной волны в вакууме. Толстая сплошная линия представляет результат вычисления по строгой формуле (17) полного сечения рассеяния o _sc единицей длины прямого кругового цилиндра радиуса R , моделирующего рассеиватель. Тонкая линия – по формуле борновского приближения (21).

Оптический ядерный потенциал для материала рассеивателя U = 1,81∙10^–7 эВ. Значение потенциала соответствует граничной скорости ОХН ν _гр = 5,90 м/с. Все расчётные значения представлены для нейтронов, двигающихся в вакууме со скоростями 6 < ν _n < 100 м/c. Значения радиусов цилиндров представлены в подписях к рисункам.

Полное время вычисления результатов, представленных на рис. 1, меньше 10 секунд на ПЭВМ с процессором Intel Core I5 (тактовая частота процессора – 2,4 ГГц.). По мере увеличения значения радиуса R время работы программы увеличивается до одной минуты за счёт увеличения значения n , при котором останавливается суммирование в формуле (17). При написании

^x ( n R ²)² [см]

и полного сечения упругого рассеяния 2 п

2 п

= 8 П ( Nb c n R ²)²j k

А ф = к d 9 1 _B

J 1 (2 kR sin 9 /2) 2 kR sin 9 /2

А ф (21)

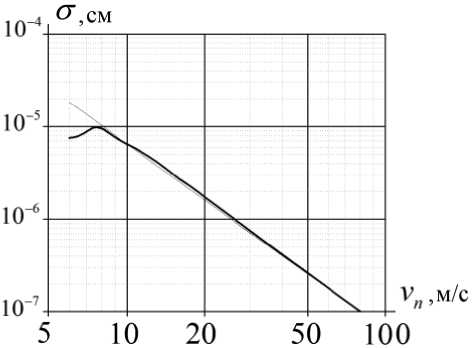
Рис. 1. Полное сечение упругого рассеяния ОХН на цилиндре с радиусом R = 25 нм

в борновском приближении.

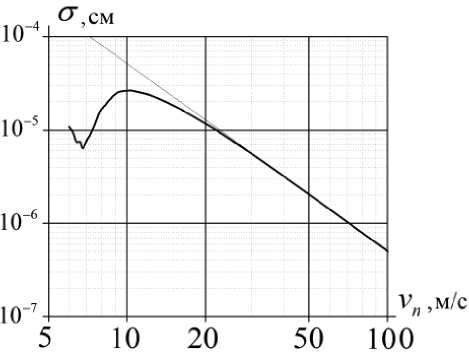
Рис. 2. Полное сечение упругого рассеяния ОХН на цилиндре с радиусом R = 50 нм

программы в качестве языка программирования использовался Фортран-90.

Из представленных в данном разделе результатов видно, что формулы, полученные в борновском приближении, можно использовать для интерпретации экспериментальных данных только для сплошных трубок, внешний радиус которых R <  50 нм. При увеличении радиуса на интервале скоростей от 6 до 20 м/сек на графиках наблюдаются дополнительные минимумы и максимумы, отсутствующие в результатах, полученных в борновском приближении. Различие между строгим и приближённым решениями в несколько раз превосходит ошибку измерения полного сечения рассеяния с помощью время-пролётного спектрометра ОХН [6].

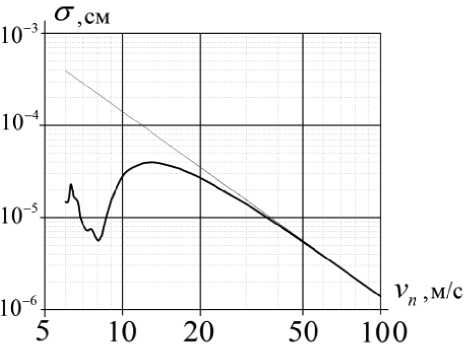
Рис. 3. Полное сечение упругого рассеяния ОХН на цилиндре с радиусом R = 70 нм

В заключение отметим, что методика определения параметров углеродных нанотрубок основана на анализе экспериментальных данных по рассеянию очень холодных нейтронов при прохождении нейтронов через образец и математическом моделировании этого процесса. Алгоритмы, представленные в этой статье, позволяют вычислять полные сечения упругого рассеяния, необходимые для такого моделирования.

ВЕСТНИК 2014. ВЫПУСК 4