Численное моделирование поперечного обтекания пролетных строений балочных мостов

УДК 533.6, 624.046.3                                      

1,2,3 Novosibirsk State Technical University, Novosibirsk, Russian Federation

Введение. Известно, что обтекание ветром инженерных сооружений носит, как правило, нестационарный турбулентный характер, в потоке наблюдаются разномасштабные вихревые структуры [1, 2]. Вблизи плохообтекаемых тел (к которым, в частности, относятся пролетные строения мостов) возникают нестационарные отрывные зоны [3]. В связи с этим адекватное моделирование эффектов турбулентности становится важным требованием к методике вычислительного эксперимента.

Для оценки аэродинамики сооружений используется моделирование крупных вихрей (Large Eddy Simulation, LES) и гибридное описании потока (Detached Eddy Simulation, DES). Однако применение указанных методов осложнено их повышенной ресурсоемкостью, причины которой:

— трехмерность задачи;

— высокие требования к плотности расчетной сетки в пристеночной области и в области «фокуса» [4];

— ограничения на шаг интегрирования по времени;

— относительно большая длительность временного «окна» для сбора нестационарной статистики в установившемся режиме.

В то же время известно [5], что для цилиндрических призм, близких по форме к балочным мостовым пролетным строениям, двумерный подход воспроизводит основные свойства течения (первичная неустойчивая мода в следе за телом существенно двумерна). Так, в работе [6] выполнен POD-анализ (Proper Orthogonal Decomposition — истинное ортогональное разложение) течения вблизи призмы с относительной шириной сечения В/Н =5 (Н — высота сечения). В результате установлено, что 1-я и 2-я моды возмущений двумерны (постоянны по пролету) и соответствуют переносу вихрей вдоль поверхности. Трехмерные моды изменяются по пролету на характерной длине, которая не меньше ширины сечения В.

Для оперативного предсказания аэродинамических характеристик (АДХ) мостовых сооружений и сопровождения продувок в аэродинамической трубе авторы настоящей работы использовали нестационарное двумерное моделирование на основе осредненных по Рейнольдсу уравнений Навье — Стокса (URANS-подход, Unsteady Reynolds-averaged Navier — Stokes). Его применимость к определению АДХ плохообтекаемых тел (неподвижных и колеблющихся) изучалась в ряде работ зарубежных авторов (см., например, [7]).

Механика

Материалы и методы. При постановке компьютерных экспериментов учитывались приведенные в [8– 10] рекомендации. Расчеты проводились в программе Fluent комплекса ANSYS.

Предварительно методика была отработана на тестовой задаче обтекания балок прямоугольного поперечного сечения. В итоге для описания турбулентности потока была выбрана модель переноса сдвиговых напряжений (Shear Stress Transport, SST) k — ω, подобраны параметры сетки и численного алгоритма.

Протяженность прямоугольной расчетной области в продольном направлении — (30 _40)Н, в поперечном — (14 ... 20)Н. Передняя грань обтекаемого тела отстояла от входной границы на (8 ... 12)Н.

Использовались низкорейнольдсовые сетки (безразмерное расстояние первого узла до стенки у + < 4…5), позволяющие рассчитывать отрыв и присоединение пограничного слоя. Ввиду сложности контуров обтекаемых тел строились многоблочные сетки. Внутренний, охватывающий тело, блок состоял из четырехугольных элементов, плотность которых ближе к поверхности тела увеличивалась. Непосредственно у стенки создавался слой со структурированной ортогональной четырехугольной сеткой. Область следа покрывалась сеткой из квадратных ячеек размером не более Н/15...Н/10. К внешним границам размер ячеек возрастал до Н/ 4 ...Н/3. На периметр сечения в зависимости от его формы приходилось порядка 10²...10 ³ ячеек. Общее количество ячеек варьировалось от 40–50 тысяч (для сечений простых форм) до 250–300 тысяч (для сложных). Пример расчетной сетки возле балки трапециевидного сечения с перекрытием и ограждениями приведен на рис 1.

Рис. 1. Пример расчетной сетки (фрагмент)

При решении уравнений Навье — Стокса связь скорость — давление реализовывалась с помощью алгоритма SIMPLE. Конвективные и вязкостные члены уравнений движения жидкости и переноса турбулентных параметров аппроксимировались схемами второго порядка точности.

Численное интегрирование осуществлялось неявной по времени схемой 2-го порядка точности. Шаг интегрирования At составлял (0,02 ... 0,04)Н/К (К» — скорость набегающего потока), т. е. при сходе вихрей с безразмерной частотой /Н/^ = 0,1 был приблизительно в 250-300 раз меньше периода 1//, и это обеспечивало приемлемое разрешение нестационарных параметров потока. Установившаяся вихревая дорожка обычно формировалась к моменту (60 ... 120)Н/ К » . Таким образом, общее число шагов интегрирования составляло в среднем 6000÷10000. Для сбора нестационарной статистики использовался отрезок времени, не меньший 5 периодов.

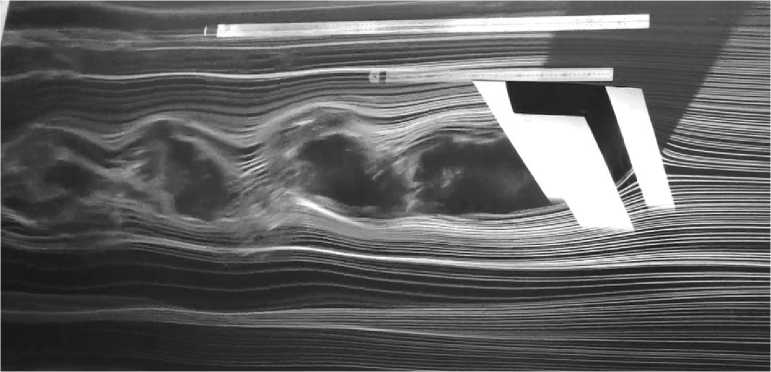
Пример качественного сопоставления расчетной и опытной картин течения вблизи пролетного строения приведен на рис. 2.

а )

б )

Рис. 2. Пример картины обтекания пролетного строения: эксперимент ( а ), расчет ( б )

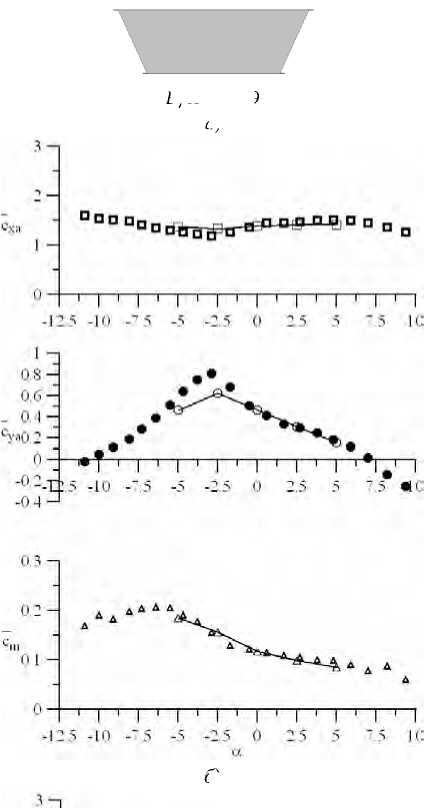
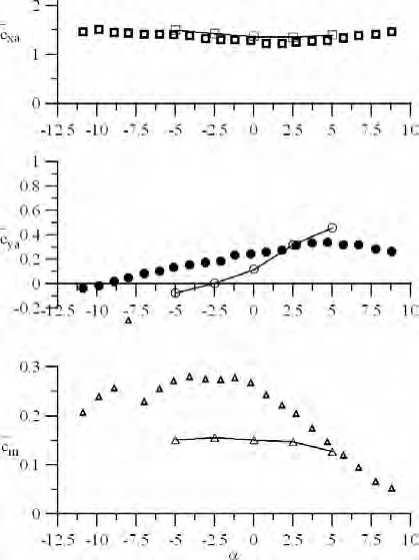
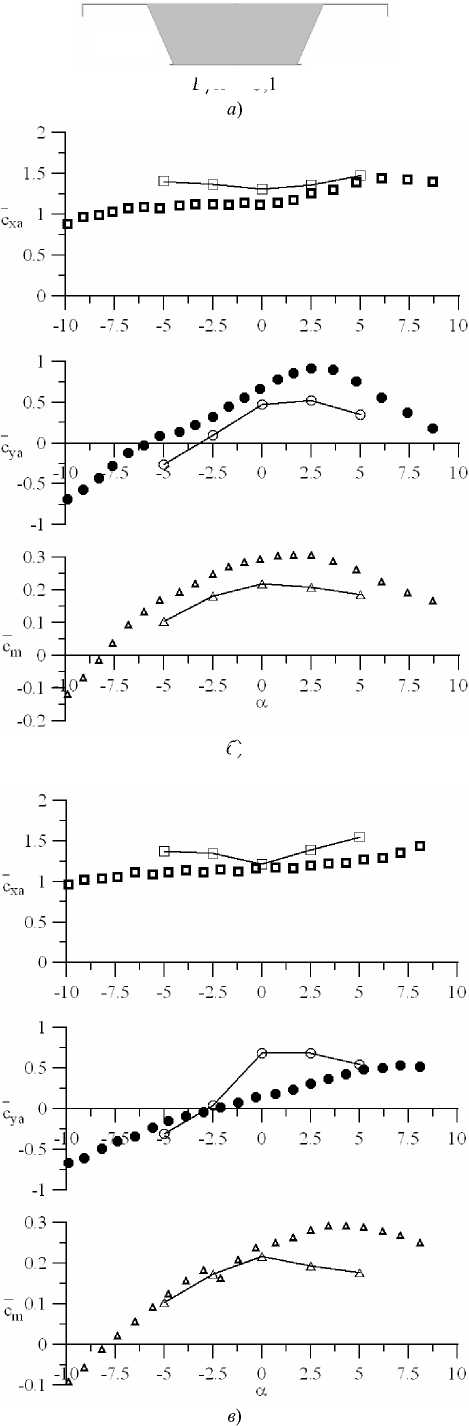
Результаты исследования. Подробные сведения по АДХ типовых поперечных сечений можно найти в [11]. На рис. 3–14 представлено сравнение расчетных и опытных данных по коэффициентам осредненных аэродинамических сил (лобового сопротивления, подъемной силы) и момента для некоторых характерных сечений.

Механика

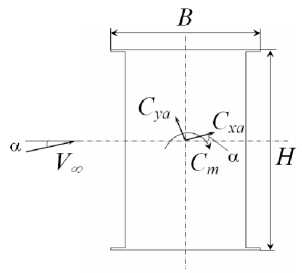
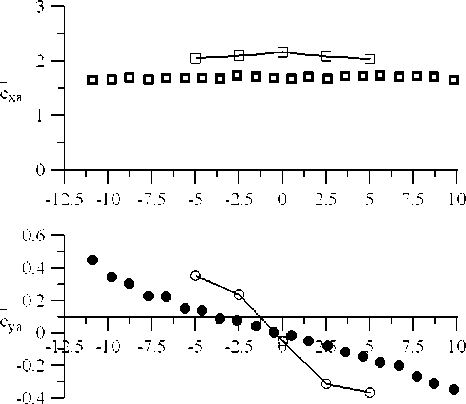
Рис. 3. Коэффициенты осредненных аэродинамических сил.

Здесь: С_ха — лобовое сопротивление; С_уа — подъемная сила; С_т — момент;

В и Н — продольный и поперечный размеры сечения (без учета ограждений); а — угол атаки

Набегающий гладкий поток характеризуется интенсивностью 0,5 %, турбулентный — 8 %. Расчетные данные представлены сплошными линиями.

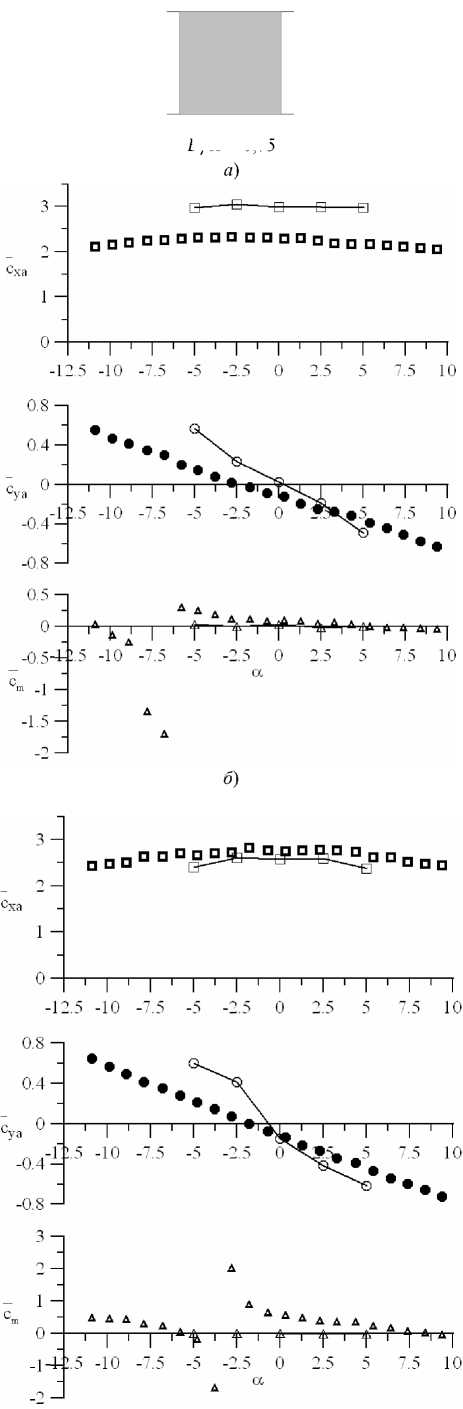
В/Н =0,75

в )

В/Н =1,24 а )

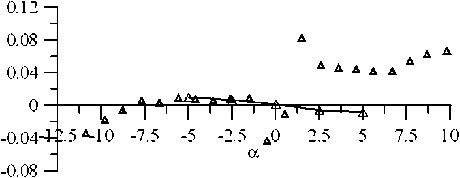
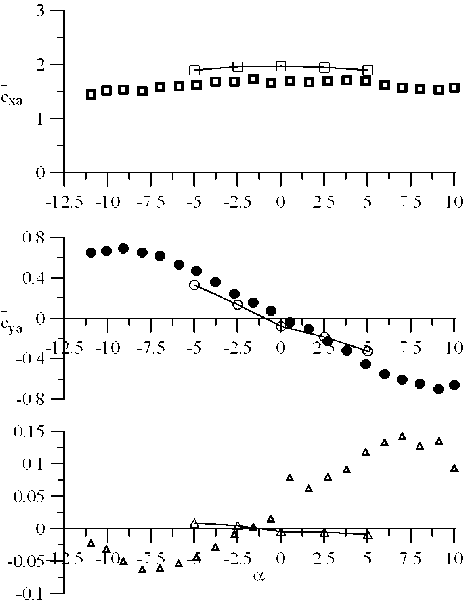
в )

Механика

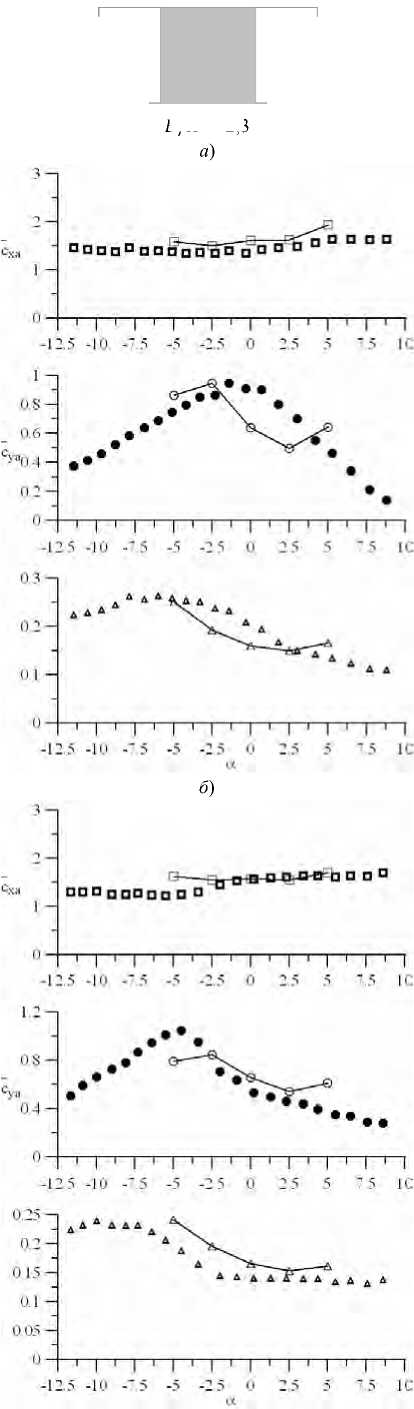
В/Н = 2,3

в )

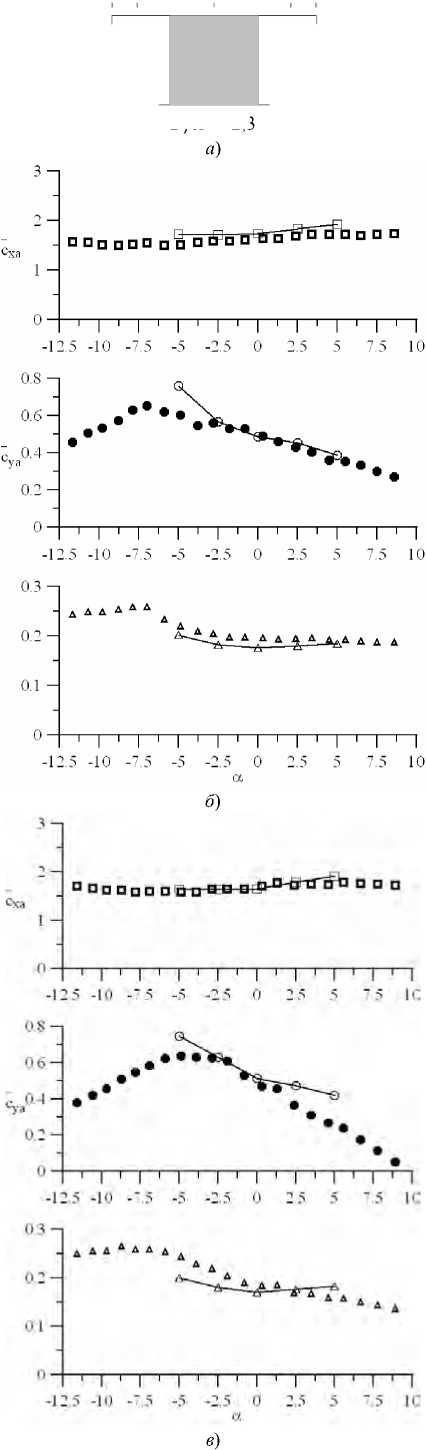
В/Н = 2,3

Механика

В/Н = 1,85 а )

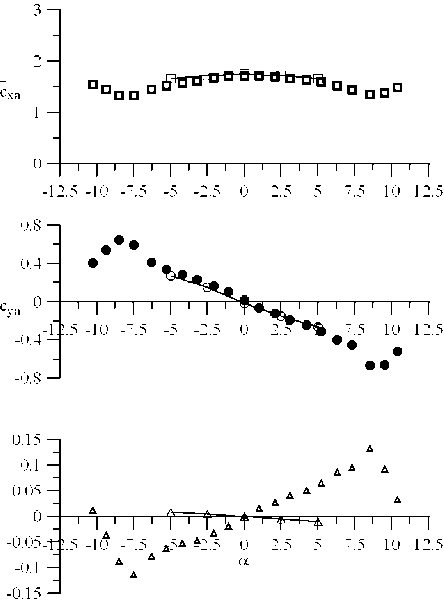
б )

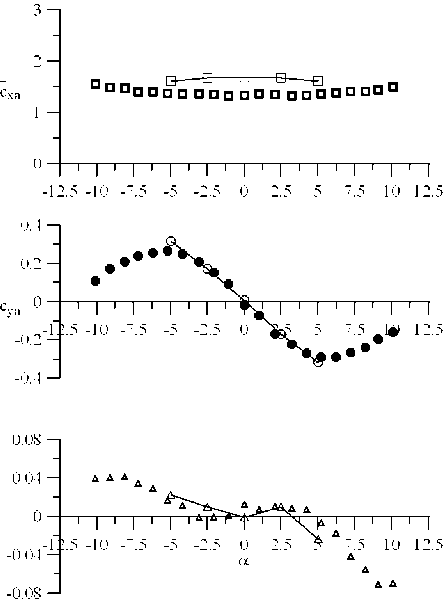
в )

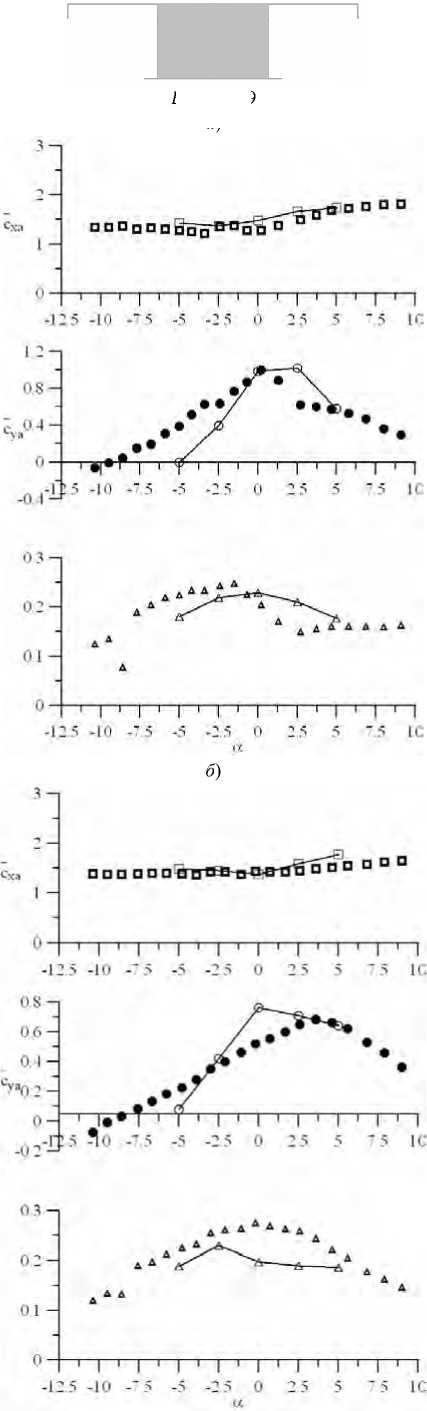
В/Н = 3,9 а )

Механика

в )

б )

В/Н = 3,09 а )

в )

б )

В/Н = 5,1

Механика

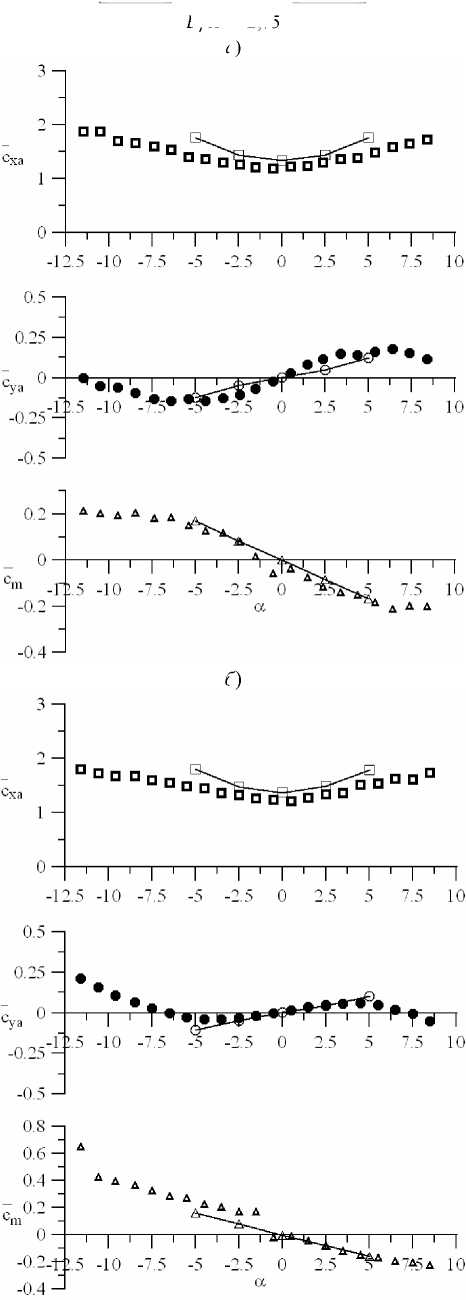
б )

В/Н = 2,75 а )

в )

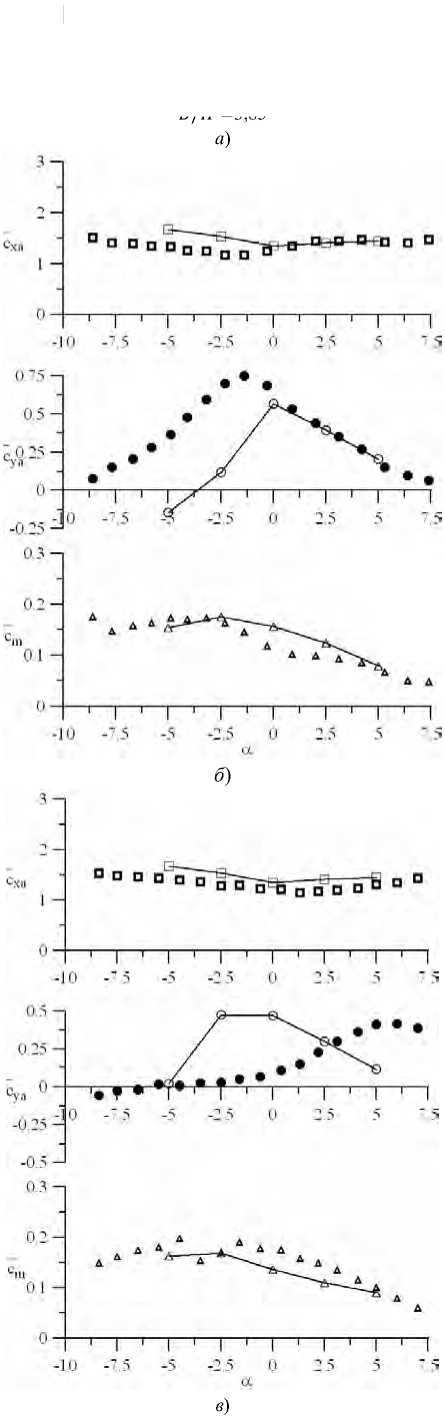
Рис. 13. Двухбалочное строениес перекрытием (соотношение B/H 3,85): форма поперечного сечения ( а ); гладкий поток ( б ); турбулентный поток ( в )

Механика

а )

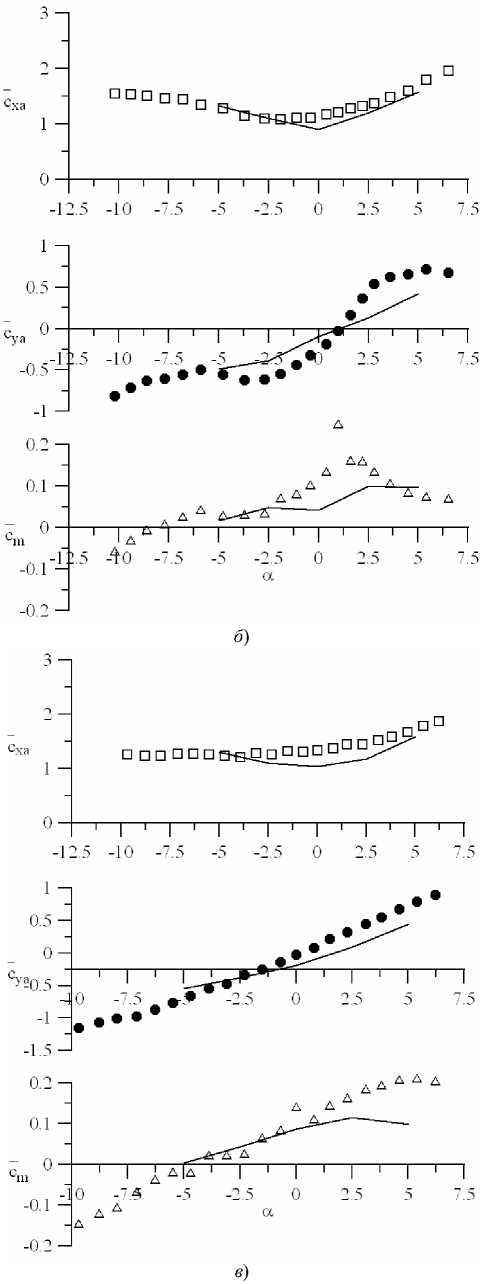
Рис. 14. Многобалочное строение с перекрытием (соотношение B/H 9): форма поперечного сечения ( а ); гладкий поток ( б ); турбулентный поток ( в )

Обсуждение и заключения. Анализируя результаты, можно отметить, что за некоторыми исключениями с увеличением относительной ширины В/Н сечения однобалочного строения точность расчетного предсказания его АДХ несколько возрастает. Как правило, наилучшее согласование отмечается по лобовому сопротивлению сечения. Для большинства конфигураций расчетные данные несколько выше коэффициента лобового сопротивления, полученного экспериментально. Поясним, что для рассматриваемых плохообтекаемых тел преобладающий вклад в лобовое сопротивление сечения вносит сопротивление формы (давления), в основном определяемое разностью сил давления на наветренной и заветренной сторонах сечения. Принятый расчетный подход огрубляет динамику вихревых структур в области за телом, что приводит к заниженному восстановлению давления в указанной области.

Величина подъемной силы более чувствительна к наличию, протяженности и типу (открыта/замкнутая) отрывных зон. Особенно это касается оснащенного плитой пролетного строения — в этом случае возможно повторное присоединение потока к верхней стороне плиты с образованием замкнутой зоны отрыва (примерно при В/Н >5). Поэтому по сравнению с лобовым сопротивлением расчетное определение подъемной силы менее точно, особенно для пролетных строений с плитой перекрытия.

Наиболее проблемным для большинства конфигураций является воспроизведение влияния угла атаки на аэродинамический момент сечения.

Если при поперечном обтекании многобалочных пролетных строений между балками возникает аэродинамическая интерференция [12], точность предсказания АДХ падает с увеличением числа балок (относительной габаритной ширины сечения). В этом случае вместо URANS-подхода целесообразно использовать более точные вихреразрешающие методы DES и LES.