Численное моделирование потока раздробленной горной массы в процессе выпуска руды с использованием программы Rocky DEM

Выпуск руды – технологический процесс извлечения обрушенной горной массы из очистного пространства через специальные выработки, расположенные, как правило, в днище блока или с торца выработки, по которой осуществляется механизированная доставка руды. Из-за конструктивных особенностей систем разработки, а также из-за перемешивания руды с вмещающими породами в процессе выпуска возникают количественные и качественные потери полезного ископаемого, что приводит к ухудшению технико-экономических показателей добычи. Поэтому понимание механизма поведения горной массы при выпуске является важным условием повышения экономической эффективности работы горнодобывающего предприятия.

Исследованиям выпуска руды посвящено значительное количество трудов отечественных и зарубежных ученых. Основополагающими для теории о выпуске являются работы Агошкова М. И., Малахова Г. М., Куликова В. В., Именитова В. Р., Дубынина Н. Г., Kvapil R. и др. [1–4]. В своих работах авторы описывают полученные в ходе исследований кинематическую и динамическую модели истечения руды, приводят закономерности поведения сыпучего материала при выпуске и предлагают расчетные схемы, позволяющие вычислять прогнозные показатели выпуска.

Методики прогнозирования и нормирования показателей извлечения руды, разработанные на основе теории о выпуске, с необходимыми для конкретных условий доработками достаточно широко применяются на горнодобывающих предприятиях России и стран СНГ. Однако рассчитанные по ним значения показателей имеют, как правило, определенную погрешность, которая может составлять до 25 % от фактических. Одна из причин этого – использование в процессе исследования лабораторных стендов, не позволяющих учесть ряд важных особенностей поведения раздробленной горной массы при ее выпуске в реальных условиях. Как правило, для исследований используют визуальные методы наблюдения, основанные на фиксации геометрии границ искусственно создаваемых слоев по мере выпуска порций материала [5]. Данные методы исследований в силу их трудоемкости и низкой вариативности не позволяют комплексно изучать механизм взаимодействия кусков (в том числе разного размера и формы) при выпуске, что требует введения дополнительных коэффициентов для большего соответствия полученных зависимостей реальным условиям [6].

Развитие методов геоинформационного обеспечения горных работ предъявляет новые требования к точности прогнозирования параметров выпуска отбитой руды [7], что достигается использованием методов численного моделирования. Существующие методы численного моделирования процесса выпуска руды позволяют с приемлемой для производственных целей точностью рассчитать прогнозные показатели извлечения, построить планограммы выпуска и проанализировать по полученным результатам эффективность того или иного варианта применяемой технологии. Анализ известных на сегодня программ [8] показал, что существующие на их основе методы прогнозной оценки показателей выпуска требуют существенных уточнений. Особенно это актуально для оптимизации конструктивных элементов системы разработки с подэтажным обрушением и торцовым выпуском руды ввиду слабой применимости к данным условиям методов, основанных на эллипсоиде выпуска1 [9–10]. Улучшить данные методики возможно, используя более совершенные виды моделирования поведения раздробленной горной массы, основанные на цифровом подобии реального механизма взаимодействия кусков различных форм и размеров в процессе их перемещения.

Материалы и методы

В качестве инструмента для теоретических исследований была выбрана программа для моделирования поведения сыпучих сред, использующая в качестве математического аппарата метод дискретных элементов (МДЭ), предназначенный для расчета результата взаимодействия большого количества частиц, таких как галька, молекулы, песчинки и т. д. Поскольку раздробленный массив горных пород можно рассматривать как сыпучую среду, а процесс выпуска – как взаимодействие большого количества частиц, то это позволило применить МДЭ для моделирования процесса выпуска руды.

В результате анализа доступных платформ, реализующих МДЭ, было решено использовать для создания модели выпуска руды программный продукт ROCKY DEM, позволяющий моделировать частицы несферической формы и задавать сыпучей среде неоднородный гранулометрический состав.

Использование МДЭ и программных платформ, реализующих его, для моделирования сыпучих сред в горнодобывающей промышленности достаточно распространено [11–13], однако условием, необходимым для получения достоверных результатов, является точность настройки применяемых моделей расчета и характеристик материала.

Программа ROCKY DEM использует следующие физические модели расчета: тангенциальных и нормальных сил взаимодействия, адгезии, сопротивления качению и др. Для каждой модели можно выбрать алгоритм расчета, влияющий на конечные результаты моделирования.

В качестве характеристик материала используются: плотность, модуль Юнга, гранулометрический состав, форма кусков, сопротивление качению, коэффициенты статического и динамического трения, коэффициент реституции, расстояние начала действия сил адгезии между частицами и величина силы адгезии в долях от силы тяжести. Поскольку некоторые перечисленные свойства не являются справочными величинами, возникает необходимость их подбора.

Одним из методов, широко используемых для калибровки сыпучих материалов в численной модели, является измерение угла естественного откоса (УЕО) при высыпании материала из цилиндрической емкости на горизонтальную поверхность [14]. В качестве исходного материала для калибровки были взяты подкрашенные куски апатит-нефелиновой руды размерами 20–35 мм, которыми заполнялся вертикально расположенный цилиндр диаметром 100 мм на высоту 200 и 400 мм, после чего форма медленно поднималась вверх, и частицы рассыпались по горизонтальной площадке, формируя УЕО (рис. 1, а). Различная высота засыпки цилиндра выбиралась для получения большей точности численной модели, так как углы естественного откоса в таких случаях составляли разные величины. Для получения большей точности измерения процесс был повторен 10 раз для каждой высоты засыпки цилиндра. Большее количество измерений не понадобилось, так как получаемые горизонтальный радиус и высота горки практически не изменялись. В результате средние значения УЕО составили 29,5° для высоты слоя 200 мм и 27,2° для цилиндра, заполненного на 400 мм.

Для численной модели значимые характеристики материала подбирались таким образом, чтобы максимально точно повторить сформированные в физическом эксперименте УЕО, а также поведение сыпучей среды в целом (рис. 1, б, в). В результате выполненной серии численных калибровочных расчетов были подобраны характеристики материала, представленные в табл. 1. Отклонение от средней величины УЕО, полученного в физическом эксперименте, составило менее 1 %. На рис. 1, в изображен результат программного вычисления угла в ROCKY DEM, где θ – полученная величина УЕО; σ – стандартное отклонение; зеленые ромбы представляют собой среднюю высоту расположения куска для каждого радиального положения (на основе всех круговых секторов); красная линия – линия регрессии, по которой вычисляется θ; правая часть рисунка показывает измерение УЕО по каждому сектору/куску.

С использованием данных табл. 1 был произведен ряд численных экспериментов для проверки соответствия модели общепринятым положениям теории выпуска, связанным с влиянием на процесс истечения формы кусков, разнородности гранулометрического состава, геометрических параметров области моделирования.

Одной из задач, решаемых в рамках эксперимента, являлась оценка влияния тех или иных факторов на механизм взаимодействия кусков с целью упрощения модели и ускорения вычислений.

а

б

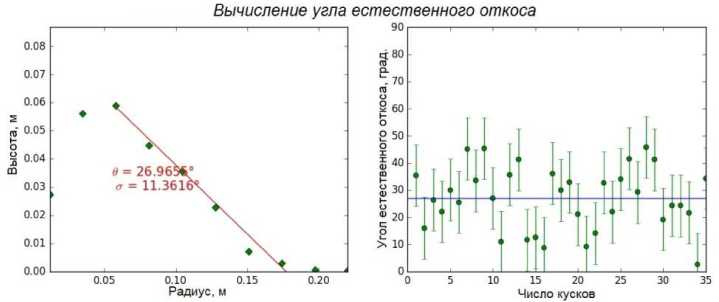
Рис. 1. Валидация сыпучей среды: а – физический эксперимент;

б – моделирование в ROCKY DEM; в – вычисление угла в ROCKY DEM Fig. 1. Bulk validation: a – physical model; б – ROCKY DEM simulation;

в – ROCKY DEM repose angle calculation

Таблица 1. Подобранные характеристики материала Table 1. Selected material characteristics

Параметр	Значение
Сопротивление качению	0,15
Коэффициент статического трения	0,75
Коэффициент динамического трения	0,7
Коэффициент реституции	0,15
Расстояние начала действия сил адгезии между частицами, м	0,002
Величина силы адгезии в долях от силы тяжести	0,1

Результаты и обсуждение

Для ускорения расчетов численные эксперименты производились на моделях бункеров, представляющих собой простую геометрическую форму (параллелепипед, цилиндр) с отверстием круглой формы в нижней ее части (рис. 2). Размеры модели в плане 2,4 × 2,4 м, высота 3 м. Диаметр отверстия 0,5 м. Гранулометрический состав среды однородный с размерами кусков 0,09 м. Модель бункера формировалась послойной засыпкой моделей кусков до верхней границы. Слои сыпучего материала одинаковой толщины. Общее число кусков от 30 до 50 тыс. После заполнения расположенная у отверстия заслонка убиралась, и начиналось свободное истечение материала. В ряде экспериментов бункер сверху постоянно пополнялся новыми порциями кусков.

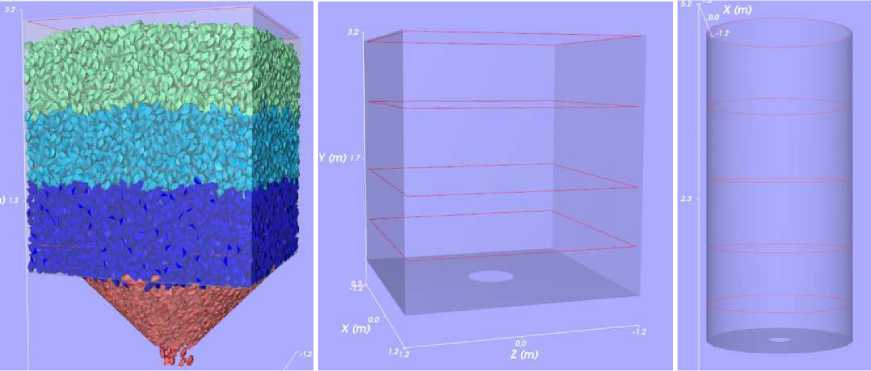
б

в

Рис. 2. Примеры моделей бункеров: а – параллелепипед с воронкой, угол откоса 45° (засыпан кусками); б – паралелепипед с плоским дном; в – цилиндр

Fig. 2. Hopper models: a – parallelepiped with chute, slope angle of 45° (filled with particles); б – parallelepiped with flat bottom; в – cylinder

Анализ численных экспериментов показал, что на результаты существенное влияние оказывают форма кусков, гранулометрический состав среды, геометрические параметры бункера и состояние материала. Упрощение модели путем использования кусков сферической формы приводит к многократному ускорению расчетов, но в то же время значительно изменяет поведение материала. Куски сферической формы стремятся достигнуть выпускного отверстия по траектории, близкой к прямолинейной. Характер перемещения несферических кусков аналогичен описанному в ряде публикаций [1–4]. Кроме того, в модели со сферическими частицами скорость истечения выше, а частицы из верхних слоев гораздо раньше достигают выпускного отверстия. Для примера в табл. 2 представлен послойный выход сыпучего материала из бункеров, изображенных на рис. 3, а, б, с указанием общей массы выпущенных кусков и процентного содержания каждого слоя в этой массе. Из табл. 2 следует, что скорость внедрения слоев сыпучего материала при использовании кусков сферической и несферической формы различна, это наиболее значимо проявляется в количестве выпущенных частиц 4-го слоя. В моделях других бункеров сохранялась та же тенденция.

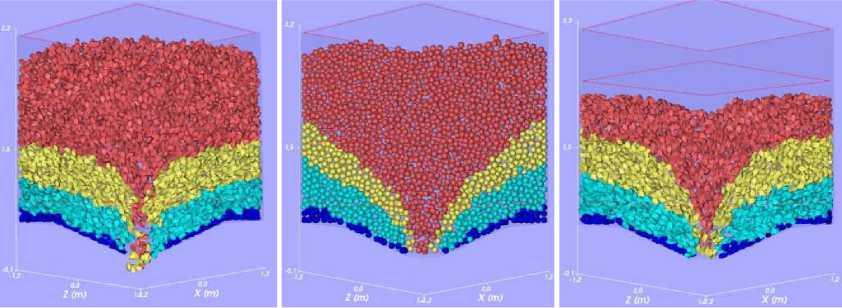
а                              б                             в

Рис. 3. Развитие воронки внедрения в модели через 60 с после начала выпуска: а – несферические частицы; б – сферические частицы;

в – несферические частицы, модель без пополнения

Fig. 3. Infiltration of the layers of matreial after 60 s of draw:

a – faceted particles; б – spherical particles; в – faceted particles, non-rechargeable model

На рис. 3, а–в представлен вертикальный разрез модели и показано положение воронки внедрения через 60 с после начала выпуска в режиме свободного истечения.

Таблица 2. Послойный выпуск материала из бункеров Table 2. Layer-by-layer release of material from the bunkers

о	Выход сыпучего материала
	Сферические куски					Несфе		рические куски
	Общий, кг	1 слой, %	2 слой, %	3 слой, %	4 слой, %	Общий, кг	1 слой, %	2 слой, %	3 слой, %	4 слой, %
12	2323,2	32,5	60,1	7,4	0,0	1857,1	45,4	54,6	0,0	0,0
22	4738,0	23,8	53,2	23,0	0,0	3700,4	38,0	57,6	4,4	0,0
32	7235,9	20,4	48,6	29,9	1,1	5319,7	33,7	57,9	8,5	0,0
42	9698,3	18,2	44,6	32,4	4,9	7176,7	29,5	55,7	14,8	0,0
52	12113,1	16,5	41,5	32,7	9,4	8963,1	26,7	54,2	19,2	0,0
62	14644,0	14,9	38,5	32,0	14,6	10918,4	23,9	50,8	24,5	0,7
72	17104,0	13,5	36,0	31,3	19,2	12654,6	21,8	49,0	26,8	2,4
80	18944,7	12,6	34,3	30,4	22,7	14102,9	20,2	47,5	27,8	4,5

На рис. 4 показаны траектории движения сферических и несферических частиц в процессе выпуска.

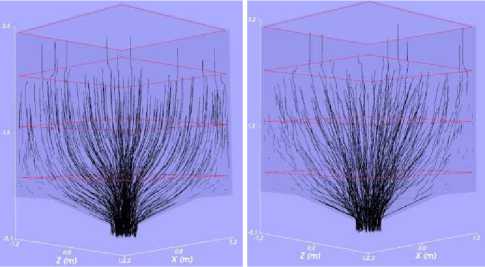
а                       б

Рис. 4. Траектории перемещения частиц при выпуске: а – несферические частицы; б – сферические частицы Fig. 4. Particles' trajectories during the simulations: a – faceted particles; б – spherical particles

Анализ траекторий движения частиц проводился с целью проверки гипотезы, по которой время перемещения куска из начального положения к конечному (выход из выпускного отверстия) зависит от его положения (расстояния и угла) относительно центра выпускного отверстия. Если отверстие круглой или любой другой формы (с определенной высотой над ним), такие куски образуют окружность в горизонтальной плоскости с центром над осью выпускного отверстия, представляя срез эллипсоида выпуска. Отслеживание их траекторий дало следующие результаты: куски двигались симметрично относительно оси выпускного отверстия, однако скорости их перемещения не были равными. Вероятно, это связано с несферичностью формы кусков, которая влияет на характер истечения. Траектории движения частиц и их исходные положения показаны на рис. 5.

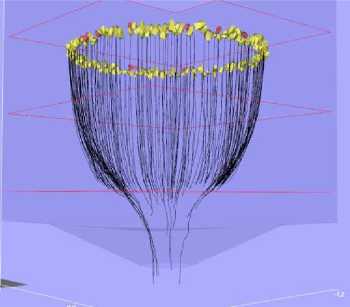
Рис. 5. Траектории перемещения частиц при выпуске Fig. 5. Particles' trajectories during the simulations

Анализ траекторий движения кусков показал отличие результатов численных экспериментов от используемых в теории о выпуске. Принято считать, что в случае донного выпуска кусок, попадающий в зону влияния только одного отверстия, движется к нему по параболической траектории. Анализ результатов численных экспериментов показал, что траектория движения кусков к выпускному отверстию по форме больше похожа на график кубической функции, чем на параболу. По параболической траектории куски стремятся не к выпускному отверстию, а к центральной зоне потока, обладающей наибольшей скоростью движения. Приблизившись к ней на некоторое расстояние, частица плавно меняет направление перемещения и опускается к выпускному отверстию по траектории, близкой к прямолинейной.

На рис. 6 показан вертикальный разрез с траекториями движения кусков, расположенных на расстоянии 0,35, 0,6 и 1 м от оси выпускного отверстия (отображение частиц отключено). Из рис. 4, а, 5 и 6 видно, что если рассматривать траекторию движения каждого отдельного куска, то ее форма может быть описана квадратичным уравнением параболы только до момента приближения к зоне потока. Если же описывать всю кривую, то необходимо воспользоваться кубическим полиномом. Причем кривизна траектории зависит от первоначального положения куска, в особенности от расстояния до оси выпускного отверстия, что при математическом описании отражается в коэффициентах кубического полинома. По графикам траекторий движения отдельных частиц с применением методов математической статистики пакета программ Microsoft Office Excel были построены линии тренда, описываемые квадратичными и кубическими функциями. Коэффициенты достоверности R ² для указанных полиномов составили 0,867–0,895 и 0,975–0,986 соответственно.

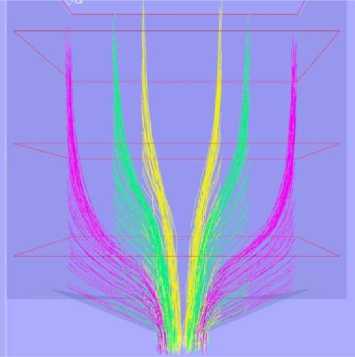
Рис. 6. Траектории перемещения частиц при выпуске Fig. 6. Particles' trajectories during the simulations

Таким образом, результаты моделирования позволяют изменить представления о траектории движения кусков, что после более тщательного исследования может быть использовано для прогнозирования результатов выпуска руды.

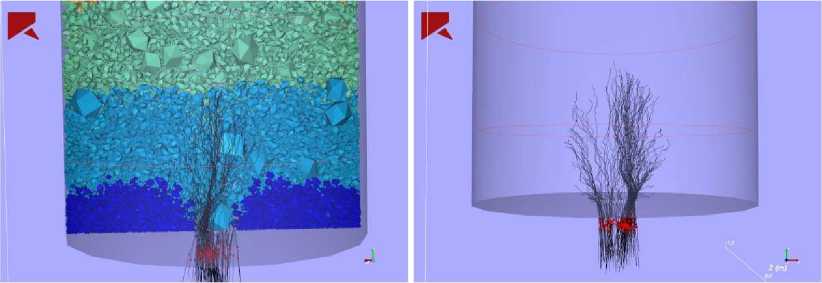
Также для получения корректных результатов исследования создаваемая численная модель выпуска руды должна быть максимально приближена к реальным условиям, в которых гранулометрический состав сыпучей среды значительно неоднородный [8]. Влияние указанной характеристики на результаты выпуска весьма существенно, однако в литературных источниках оно описано лишь с качественной стороны. Для проверки влияния неоднородности гранулометрического состава на процесс истечения был смоделирован выпуск сыпучей среды из цилиндрического бункера диаметром 2,4 м через круглое выпускное отверстие размером 0,5 м (рис. 7, а). Кусковой материал состоял из частиц размером от 0,02 до 0,45 м.

б

а

Рис. 7. Моделирование выпуска дисперсного гранулометрического состава Fig. 7. Grading drawing simulation

Схема истечения была аналогична предыдущим экспериментам, однако значительное различие в размерах кусков вносило свои коррективы – мелкие куски стремились заполнять пространство между крупными, опережая их. Крупные куски наоборот, даже попав в зону центрального потока, не ускорялись, вынуждая более мелкие куски обтекать себя и менять геометрию зоны потока (рис. 7, а, б). Такие явления согласуются с результатами, полученными другими авторами, что также может качественно подтверждать адекватность используемой модели.

Заключение

По результатам моделирования сделан вывод об адекватности численной модели и возможности ее использования для изучения процесса выпуска раздробленной горной массы в различных технологических схемах. Показано, что на результаты выпуска существенное влияние оказывают геометрические параметры конструктивных элементов очистного пространства, форма, гранулометрический состав горной массы и ее физико-механические характеристики.

Анализ перемещения кусков руды показал, что траектория их движения к выпускному отверстию с более высоким коэффициентом достоверности описывается не параболической, а кубической функцией. По параболической траектории куски лишь достигают центральной зоны потока. В дальнейшем данное свойство требует дополнительных исследований для уточнения существующих положений теории о выпуске руды.

В дальнейшем необходимо исследовать влияние неоднородности гранулометрического состава сыпучей среды на процесс ее истечения при выпуске. Как показали предварительные исследования, это влияние имеет весьма существенный характер. Аналогичное мнение высказывается в [10], где подчеркивается, что появление вблизи выпускного отверстия крупных негабаритных кусков приводит к изменению характера истечения раздробленной горной массы и появлению в выпускном отверстии пустых пород гораздо раньше планируемого срока. Таким образом, выполненные исследования показали высокий потенциал численного моделирования на основе МДЭ для изучения механизма поведения раздробленной горной массы и решения на этой основе задач оптимизации процесса выпуска применительно к различным технологическим схемам.