Численное моделирование поведения кинематически нестабильных склонов при динамических воздействиях

Введение . В 70-х годах прошлого века началось широкое использование метода конечных элементов (МКЭ) при анализе статической устойчивости склонов и откосов [1–3]. Как показала практика геотехнических расчетов МКЭ в отличие от упрощенных методик позволил учесть такие важные факторы как реальную геометрию и послойную структуру исследуемых объектов, а также наличие противооползневых сооружений и физическую нелинейность материала с заранее неизвестной областью пластичности [4]. В настоящее время многие исследователи стали применять МКЭ для анализа динамической устойчивости склонов реального заложения, а также прогнозирования рисков обвалов горных пород в подземных выработках и со склонов, расположенных вдоль автомобильных и железнодорожных магистралей. Также одним из актуальных направлений горной динамики является конечно-элементное моделирование последствий землетрясений с учетом кинематической нестабильности конгломераций [5]. В настоящее время существуют следующие методы динамических расчетов в области геотехники:

• 1.    SRM (strength reduction method) — метод снижения прочности [6, 7]. Разработан для расчета запаса прочности горного массива в физически нелинейной постановке. В SRM фактические прочностные параметры грунта итерационно уменьшаются путем деления на некоторый коэффициент больше 1:

• 2.    LEM (limit equilibrium method) — метод предельной кинетики, базирующийся на принципе Даламбера [8, 9]. Ориентирован на анализ динамической устойчивости сочлененных массивов горных пород.

• 3.    TLEM (thin layer element method of FEM) — метод тонкослойных конечных элементов [10], в котором упругопластические элементы тонкого слоя используются для моделирования поведения кинематически нестабильных структур.

г л

. c                  tanф c =----; ф = arctan ----- , kSRM                ^ k SRM у где c, ф — фактические значения сцепления и угла внутреннего трения грунта соответственно; c', ф' — сцепление и угол внутреннего трения грунта соответственно после их уменьшения относительно фактических значений; kSRM — коэффициент снижения сдвиговой прочности. Величина kSRM , соответствующая предельному состоянию системы, определяет нижнюю границу прочностных параметров материала.

Анализ результатов, полученных с помощью методов SRM, LEM и TLEM, показал, что в настоящее время отсутствует единая концепция математического моделирования поведения структурно нестабильных геотехнических систем при нестационарном внешнем воздействии. Это обусловливает актуальность разработки методики динамического анализа систем типа «основание — ослабленный слой — блок» в конечно-элементной постановке с использованием нового подхода к моделированию плоскостей скольжения.

Механика

Материалы и методы . Уравнение движения механической системы в конечно-элементной формулировке представим в виде [11]:

• [ M]{W " (t )} + [ C]{W ' ( t )} + [ K]{W ( t )} = { F o} + { F ( t )} ,                            (1)

где [ M ], [ C ], [ K ] — матрицы масс, демпфирования и жесткости ансамбля конечных элементов соответственно;

( W "( t )}, { W ‘ ( t )}, { W ( t )} — векторы-столбцы соответственно узловых ускорений, скоростей, перемещений; { F ₀} , { F ( t )} — векторы-столбцы заданных статических и динамических нагрузок соответственно в момент времени t . В дальнейшем полагаем, что матрицы [ M ] и [ K ] согласованные.

Для численного интегрирования уравнения (1) используем метод Ньюмарка [12]. При этом шаг интегрирования по временной оси A t назначаем так, чтобы с достаточной точностью учитывались вклады физически значимых собственных пар. В дальнейшем рассмотрим кинематические способы возбуждения колебаний, заданные с помощью либо модельной сейсмограммы { W ( t )}, либо с помощью модельной акселелограммы { W " ( t )}. При таком способе задания динамического воздействия второе слагаемое правой части уравнения (1) будет равно нулю: { F ( t )} = 0.

Рассмотрим способ возбуждения механических колебаний посредством модельной сейсмограммы. Функцию W ( t ) представим в виде [13]:

W ( t ) = Ate ^{- x t} sin( 0 t ),                                               (2)

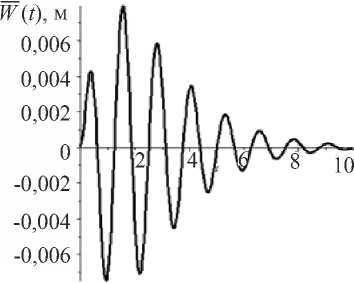
где A — начальная амплитуда; х — коэффициент затухания; 0 — угловая частота внешнего воздействия. На рис. 1. приведен график функции W ( t ) для значений: A = 0,01553 м; х = 0,7143; 0 = 5 с^- 1 .

t ,c

Рис. 1. График модельной сейсмограммы

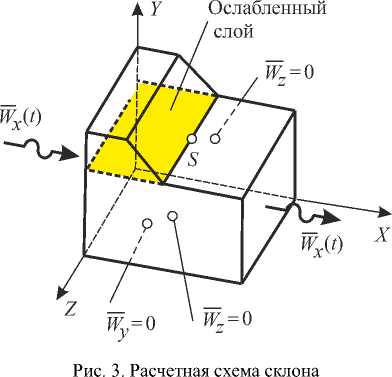
Результаты исследования. В качестве первого модельного примера рассмотрим задачу о вынужденных колебаниях склона, расположенного на основании (рис. 2). Граничные условия задачи показаны на рис. 3, где

буквой А обозначена исследуемая точка.

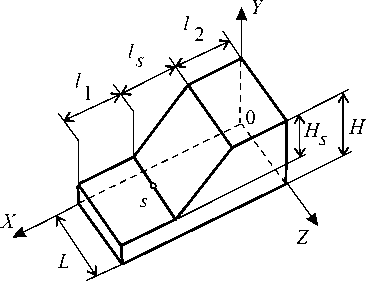
Рис. 2. Геометрия склона

Соотношения геометрических параметров склона и основания (рис. 2) представлены в таблице 1.

Соотношения геометрических параметров

Таблица 1

H	1 1	l s	1 2	L
3,5 H s	H s	(1,0 - 2,0) H s	H s	5 H s

Механические характеристики материала склона и основания: модуль деформации Е = 21 МПа; коэффициент Пуассона v = 0,3; удельный вес у = 1702 кг/м ³ ; сцепление с = 45 кПа; угол внутреннего трения ф = 15°.

Для моделирования склона и основания используем объемные конечные элементы SOLID45 программного комплекса ANSYS Mechanical. Конечно-элементная модель для варианта с параметрами: l _s = 2 H_s , H _s = 10 м, отнесенная к глобальной декартовой системе координат, приведена на рис. 4.

Конечно-элементная сетка построена таким образом, что на поверхности контакта смежные узлы основания и склона имеют одинаковые координаты, но разные номера. Это принято для того, чтобы разместить в этом месте ослабленный слой. Кинематическое воздействие в форме модельной сейсмограммы (2) задаем на каждом шаге интегрирования ti в виде узловых перемещений Wx(ti) на торцовых поверхностях модели с параметрами: X = 0 и X = l1 + IS +l2.

Моделирование ослабленного слоя (рис. 4) выполняем с помощью упруго-вязких комбинированных конечных элементов COMBIN14 [14]. Двухузловой элемент COMBIN14, состоящий из пружины жесткостью k и демпфера жидкостного трения с коэффициентом демпфирования сv , приведен на рис. 5. В рассматриваемом случае этот элемент работает только на растяжение-сжатие.

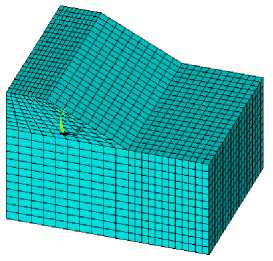
Рис. 4. Конечно-элементная модель системы «основание — склон»

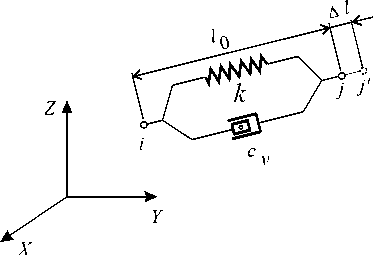
Рис. 5. Комбинированный конечный элемент COMBIN14

В каждом узле контактной поверхности (рис. 4) вдоль глобальных осей X , Y , Z вводим элементы COMBIN14. Параметры комбинированных элементов:

k = 30 кН/м; k = k = 9,44∙10 ⁷ кН/м; с = 0,5. x yz v

В этом примере и далее вводим допущение о естественном недеформированном состоянии системы «основание — ослабленный слой — склон». Для вычислений используем нелинейный решатель комплекса ANSYS Mechanical.

Результаты конечно-элементного моделирования в виде визуализации деформированного состояния системы «основание — склон» с учетом максимального горизонтального смещения и распределения амплитудных горизонтальных перемещений Wx (t) показаны на рис. 6 и 7. Шаг интегрирования уравнения (1) A t = 0,01 с. Как видно, введение 3D упруго-вязких элементов позволяет смоделировать эффект кинематической нестабильности механической системы «основание — ослабленный слой — склон» при кинематическом способе возбуждения колебаний.

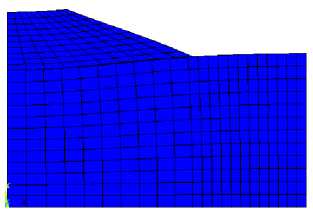
Рис. 6. Визуализация смещения склона относительно основания

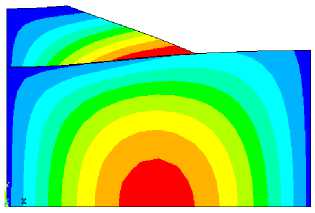
W x ( t ) , м

.002535 .004178 .005822 .007465 .009109 .010752 .012395 .014039 .015682 .017326

Механика

Рис. 7. Распределение перемещений W_x ( t )

Амплитудное значение перемещения в точке 5 составило W x_s max = 1,7 см. Для варианта склона l _s = H _s (рис. 2) W x_{s max} = 1,1 см. Графики колебаний основания и склона в исследуемой точке 5 (рис. 3) в направлении оси X приведены на рис. 8.

Wx +( t ), Wx- ( t ), м

0,02

0,01

-0,01

-0,02

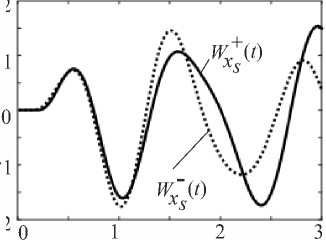
t , c

Рис. 8. Графики колебаний в точке 5 основания W x + ( t ) и склона W x - ( t ) при кинематическом возбуждении с помощью модельной сейсмограммы

На основании приведенных графиков видно, что начиная с момента времени t > 1,5 с наблюдается рассогласование колебаний основания и склона.

Рассмотрим поведение системы «основание — ослабленный слой — склон» (рис. 3) при возбуждении колебаний с помощью модельной акселерограммы W" ( t ). С этой целью дважды продифференцируем выражение (2). В результате получим:

W "( t ) = Ae" ^{x t} [ х ² sin( 9 t ) t - 2 x cos( 9 t ) 9 t - sin( 9 t ) 9²1 -

- 2 x sin( 9 t ) + 2cos( 9 t ) 9 ].

График функции (3) для параметров: A = 0,01553 м; х = 0,7143; 9 = 5 с ^{- 1} показан на рис. 9.

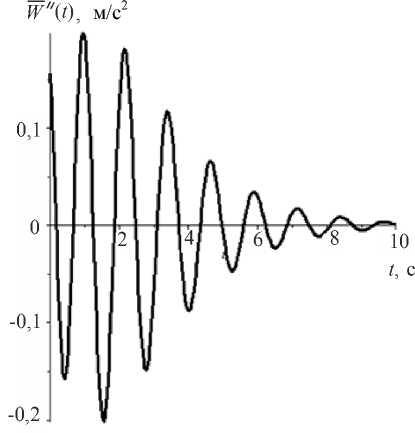
Рис. 9 . График модельной акселелограммы

Кинематическое воздействие в форме модельной акселерограммы (3) по аналогии с сейсмограммой (2) задаем на каждом шаге интегрирования t , в виде узловых ускорений W ‘ ' ( t , ) на торцовых поверхностях модели с параметрами: X = 0 и X = l 1 + l_s + l ₂ . На рис. 10 представлены графики колебаний в исследуемой точке 5 (рис. 3) при кинематическом воздействии в форме модельной акселерограммы. Сравнивая графики колебаний, приведенные на рис. 8 и 10, устанавливаем, что они практически совпадают. Это свидетельствует о корректности

разработанной конечно-элементной модели, позволяющей описывать поведение системы «основание ослабленный слой — склон» при различных способах нестационарного кинематического воздействия.

—

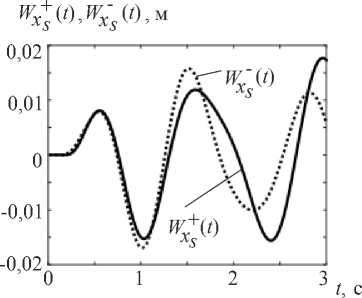
Рис. 10. Графики колебаний в точке 5 основания W x + ( t ) и склона W x _$ ( t )

при кинематическом возбуждении колебаний с помощью модельной акселелограммы

В качестве второго модельного примера рассмотрим задачу о вынужденных колебаниях склона с кинематически нестабильным клиновидным включением (рис. 11). В связи с симметрией конфигурации, в расчетной схеме учитываем только 1/2 часть склона и включения. Граничные условия для принятой расчетной схемы показаны на рис. 12. Здесь буквой S обозначена исследуемая точка, принадлежащая одновременно

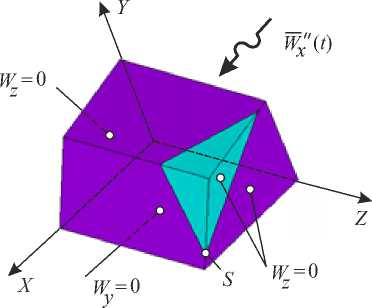
Рис. 12. Расчетная схема для задачи «склон — клиновидное включение»

основанию склона и клиновидному включению.

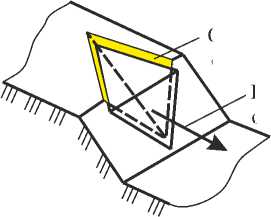
Направление скольжения

Ослабленный слой

Рис. 11. Схема склона с клиновидным включением

Конечно-элементная модель склона и клиновидного включения показана на рис. 13. Как и в предыдущем примере, в данном случае используем элементы SOLID45 и COMBIN14 с теми же характеристиками материала.

• а )                                               б )                                              в )

Рис. 13. Конечно - элементная модель : а — склон ; б — клиновидное включение ; в — склон с клиновидным включением

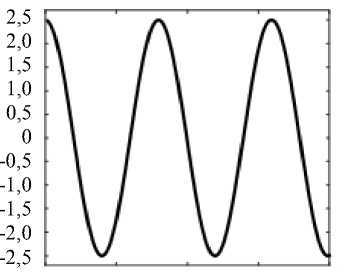
Функция, описывающая модельную акселелограмму, имеет вид: W(t) = A• cos0t, где A — амплитуда ускорения; 0 — частота внешнего воздействия. На рис. 14 приведен график Wx (t) при A = 2,5 м/с2, 0 = 2 Гц. Значения ускорения Wx (Ц) на i-том шаге интегрирования уравнения движения (1) прикладываем к узлам поверхности модели с координатой X = 0 (рис. 12).

Механика

Wx( t ), м/с ²

0   0,05      0,1     0,15     0,2

Рис. 14. График модельной акселелограммы W x ( t )

t, c

Результат моделирования в виде распределения амплитудных значений перемещений Wx (t) показан на рис. 15. Шаг интегрирования At = 0,01 с. Графики колебаний основания склона и клиновидного включения в исследуемой точке А (рис. 12) в направлении оси Xприведены на рис. 16.

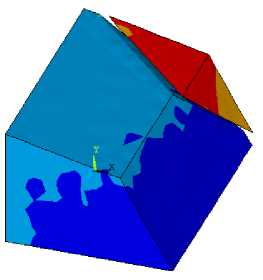
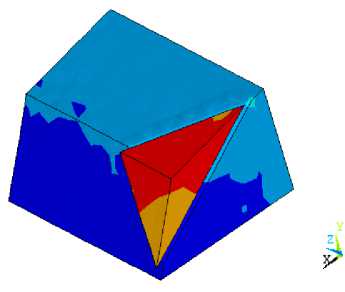
Как видно из рис. 15 при заданном кинематическом воздействии происходит разрыв сплошности массива склона по ослабленному слою и клиновидное включение смещается относительно основания склона вдоль оси X .

W x ( t ) , м

Рис. 15. Распределения W x ( t ) в 1 / 2 части склона с клиновидным включением

-.022525

-.019874

-.017224

-.014573

-.011923

-.009273

-.006622

-.003972

-.001321 .001329

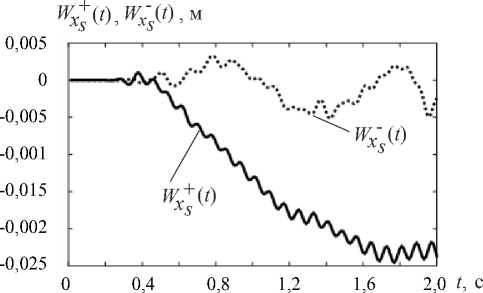
Рис. 16. Графики колебаний в точке А основания склона Wx + (t) и клиновидного включения Wx$ (t) при кинематическом возбуждении колебаний с помощью модельной акселелограммы

«Дрейф» W_x + ( t ) на рис. 16 обусловлен тем, что данная конечно-элементная модель не имеет связей, препятствующих смещениям вдоль оси X. Как показано в [11], решить проблему «дрейфа» можно путем вычитания из значений перемещений W_x + ( t ) и W_x - ( t ) перемещения основания склона, которое представляет собой смещение «как жесткое целое». Отметим, что полученные амплитудные значения перемещений W_x + ( t ) и W_x - ( t ) позволяют оценить динамические параметры системы «склон — ослабленный слой — клиновидное включение».

Заключение. Разработана и верифицирована конечно-элементная модель для исследования динамического поведения кинематически нестабильных склонов в трехмерной постановке с учетом физической нелинейности материала.