Численное моделирование процесса электронно-лучевой сварки с продольной осцилляцией луча на основе экспериментально определенной формы канала проплавления
Автор: Пермяков Г.Л., Трушников Д.Н., Беленький В.Я., Ольшанская Т.В.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 4 т.16, 2015 года.
Бесплатный доступ
Исследование посвящено изучению процесса электронно-лучевой сварки с глубоким проплавлением с применением осцилляции пучка при различной фокусировке на примере стали 15Х5М. Рассматривается влияние продольной осцилляции пучка и её параметров на форму канала проплавления, характер протекания процессов тепломассопереноса и параметры сварных швов для разработки методических рекомендаций по электронно-лучевой сварке с осцилляцией пучка. Представлена численная трёхмерная математическая модель электронно-лучевой сварки, основанная на совместном решении уравнений теплопроводности и Навье-Стокса в подвижной системе координат, с учётом фазовых переходов на границе раздела твёрдой и жидкой фазы. Граничные условия на свободной поверхности сварочной ванны и стенках канала представлены термокапиллярной конвекцией (эффект Марангони). В качестве входных параметров использовалась форма канала проплавления и распределение энергии пучка по стенкам канала, определённые на основе экспериментальных данных по параметрам вторичного сигнала в плазме над зоной сварки с помощью метода синхронного накопления. Форма канала аппроксимирована усечённым конусом со сферической вершиной. Такой подход избавляет от необходимости учета всех сложных факторов, оказывающих воздействие на формирование канала проплавления. Расчёты тепловых и гидродинамических процессов производились на кластере с использованием пакета моделирования COMSOL Multiphysics. Сравнение расчётных и экспериментальных поперечных сечений сварных швов показали хорошее соответствие. С помощью предложенной методики в ходе исследований были выявлены характерные особенности распределения мощности пучка при различных режимах фокусировки. Проведен анализ значимости различных факторов на формирование геометрии проплавления.
Электронно-лучевая сварка, осцилляция пучка, математическая модель, метод синхронного накопления
Короткий адрес: https://sciup.org/148177500
IDR: 148177500 | УДК: 621.791.722
Текст научной статьи Численное моделирование процесса электронно-лучевой сварки с продольной осцилляцией луча на основе экспериментально определенной формы канала проплавления
Введение. В настоящее время широко известны успехи, достигнутые в области численного моделирования электронно-лучевой и лазерной сварки [1-3]. Однако все результаты связаны с моделированием сварки статическим пучком. Законченные динамические модели сварки с осцилляциями пучка отсутствуют до сих пор. Комплексный характер, высокая скорость протекания процессов, высокие значения градиентов температур и многофакторность процессов делают непосредственное численное моделирование в условии периодических воздействий крайне затруднительным даже с использованием современных вычислительных ресурсов [1]. Основная трудность при моделировании - определение формы канала проплавления.
Для решения этой проблемы ранее была предложена методика экспериментального определения формы канала проплавления при электронно-лучевой сварке с осцилляцией пучка по параметрам вторичного сигнала [4]. Кроме формы канала проплавления указанная методика дает дополнительную информацию о процессах в канале проплавления. В частности, данная методика позволяет определить распределение энергии пучка по стенкам канала проплавления [5]. Такой подход избавляет от необходимости учета всех сложных факторов, оказывающих воздействие на формирование канала проплавления.
Целью данного исследования является использование данных параметров в качестве входных для проведения математических расчётов, определение влияния различных осцилляций пучка и их параметров на форму канала проплавления, протекание процессов тепломассопереноса и параметры швов для разработки методических рекомендаций.
Расчёты тепловых и гидродинамических процессов производились на кластере с использованием пакета моделирования COMSOL Multiphysics. В ре- зультате расчётов была получена геометрия сварного шва, поля температур и скоростей течения расплава.
Математическая модель. На рис. 1 показана схема модели. Параметры процесса и физические параметры стали 15Х5М представлены в табл. 1 и 2 соответственно. Следующие упрощения были сделаны при моделировании процесса сварки:
-
- ламинарное течение расплава;
-
- нормальное распределение энергии в пучке;
-
- линейный, вдоль оси X , источник тепла;
-
- моделирование фазового перехода с помощью скачка вязкости и введения скрытой теплоты фазового перехода;
-
- форма и размер канала проплавления были определены из экспериментальных данных; канал аппроксимировали усечённым конусом со сферической вершиной.
Реконструкция формы канала. Реконструкция формы канала проплавления и получение данных о распределении энергии в нем осуществлялись посредством регистрации вторичных излучений из зоны сварки методом синхронного накопления [6; 7]. На рис. 2 представлены результаты реконструкции формы канала при электронно-лучевой сварке с осцилляцией вдоль стыка на трех режимах фокусировки [3; 4]. Для наглядности масштаб вдоль вертикальной и горизонтальной осей выбран неодинаковым. Видно, что при изменении режима фокусировки изменяется характер взаимодействия пучка со стенками канала проплавления. При сварке на недофокусированном режиме электронный пучок взаимодействует в основном с передней стенкой канала проплавления, на перефокусированном - с передней и задней стенками практически одинаково. Полученная форма канала проплавления и распределение энергии пучка в нем использовались при моделировании в качестве входных параметров.
Гапи*г**г
Лдц дГм I ш границе
_ А.(нлГм1Ила цикяне
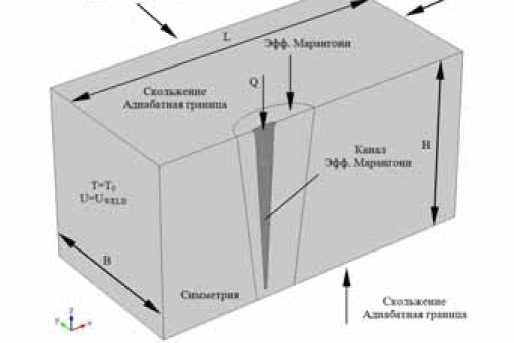
Рис. 1. Геометрия модели, начальные и граничные условия
Параметры процесса
Таблица 1
|
Тип осцилляции |
Параметры пучка |
Параметры осцилляции |
Скорость сварки У св, мм/с |
||
|
Мощность Q , кВт |
Min радиус, мм |
Амплитуда, мм |
Частота, Гц |
||
|
Продольная |
3 |
0,25 |
0,75 |
645 |
5 |
Таблица 2
Физические характеристики стали 15Х5М
|
Характеристика |
Обозначение |
Величина |
|
Начальная температура |
T 0 [K] |
293,15 |
|
Ликвидус |
T l [K] |
1730 |
|
Солидус |
T s [K] |
1700 |
|
Скрытая теплота плавления |
L f [Дж^кг-1] |
700 |
|
Динамическая вязкость |
p [Пат] |
0,007 |
|
Плотность |
р [кг^м-3] |
7750 |
|
Удельная теплоёмкость |
c [Дж^кг-1/К-1] |
483 |
|
Теплопроводность |
X |В|-м1< ' | |
37 |
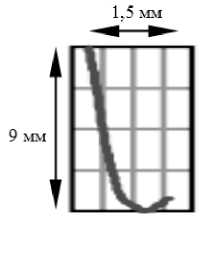
а
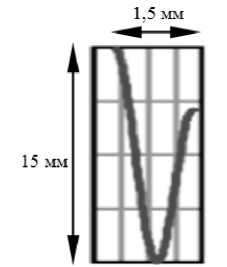
б
Рис. 2. Результаты реконструкции канала проплавления (продольная проекция) по параметрам вторичного сигнала при электронно-лучевой сварке с осцилляцией вдоль стыка для различных режимов фокусировки: а - перефокусированный; б - острый фокус; в - недофокусированный
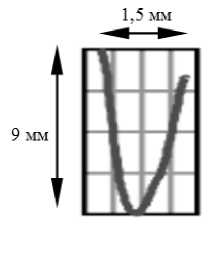
в
Основные уравнения. Модель основана на совместном решении тепловой и гидродинамической задачи обтекания жидким металлом канала проплавления в трехмерной постановке. Рассмотрим основные уравнения для расчетов [1; 8].
Течение жидкого металла описывается уравнениями непрерывности и движения для несжимаемой жидкости в подвижной системе координат:
V й = 0, (1)
р - ^ + р ( й -V ) й = p -V 2 й -V P + F , (2) где р - плотность; й - вектор скорости течения расплава; ц - динамическая вязкость; P - давление; F -слагаемое, представленное в виде
Г ^ и
F = рgа(T-Tref)-C -f й + рУй —, (3) I f3 + В J -x где g - ускорение свободного падения; а - коэффициент термического расширения; T - абсолютная температура; Tref - исходная температура, принятая как температура солидуса (TS); Усв - скорость сварки.
Первый член уравнения представляет термогравитационную конвекцию, второй член уравнения представляет диссипацию энергии в двухфазной зоне в соответствии с уравнением Кармана-Козени [9; 10], где В - небольшая вычислительная постоянная - введена для избегания деления на ноль; C - константа учёта морфологии двухфазной зоны (в данных исследованиях использовалась величина, равная 1,6-104 [10]); fL - жидкая составляющая [11]:
[ 1 T > T L ,
•(T - Ts)/(Tl - Ts) Ts < T < Tl ,
0 T < T .,
где TL и TS - температура ликвидуса и солидуса соответственно.
Последний член уравнения (3) описывает движение заготовки относительно электронного пучка.
Распределение тепловой энергии источника в заготовке может быть описано с помощью дифференциального уравнения переноса энергии:
a t
a2t a2t a2t ) at q --— H —+ + u—— H , ax2 ay2 az2 J ax cp
где T - абсолютная температура; a = X/ C f • p -коэффициент температуропроводности; u - скорость течения расплава; c - теплоёмкость; p - плотность; Q - подводимая тепловая мощность.
Скрытая теплота плавления и кристаллизации учитывалась введением эффективной теплоемкости
N f = N 0 +
exp[ - (( T - Tmelt)I(TL - Ts )) 2 ] V^ ( T l - Ts )
H f ,
где С о - теплоемкость в зависимости от температуры; H f - скрытая теплота плавления; Tmelt - температура плавления, которая принята средней в интервале от температуры солидуса до ликвидуса.
На верхней поверхности сварочной ванны и на стенках канала проплавления действует эффект Марангони. Для этих поверхностей в проекциях на оси X , Y и Z можно записать [12-15]:
au _ d у a t av _ d у a t
ц— = f--; ц— = fi;
LL az dT ax azdT aw r d у a t ц— = fl, az L dT az
где u , v , w - компоненты скорости вдоль осей X , Y и Z соответственно; ц - динамическая вязкость; fL - жидкая составляющая; d у/ dT - температурный коэффициент поверхностного натяжения; T - абсолютная температура.
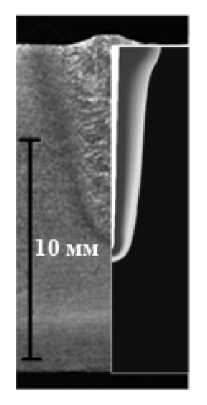
Результаты. На рис. 3 представлены экспериментальные и расчётные сечения сварных швов при сварке с продольной осцилляцией для различных режимов фокусировки.
Экспериментальные и расчётные данные для острого фокуса и перефокусированного режима хорошо согласуются. Различия между расчётами и экспери
ментом для перефокусированного режима вызваны ошибками при определении глубины канала проплавления.
Проведен анализ значимости влияния различных факторов на формирование геометрии проплавления и на вероятность формирования дефектов при электронно-лучевой сварке с осцилляцией электронного пучка. Одной из причин специфической формы проплавления с уширением в верхней части являются конвективные явления в жидкой фазе (характерные значения чисел Марангони и Рэлея составили 5-103 и 2-103). Интенсивность этих явлений зависит от распределения вводимой энергии в канале проплавления и, как следствие, от режима фокусировки. Установлено, что интенсивность конвективных течений, обусловленных эффектом Марангони, повышается при переходе от недофокусированного режима к перефокусированному. Интенсивность термогравитационной конвекции при этом несколько снижается.
Выводы. Математическая модель позволяет проанализировать влияние параметров осцилляций на геометрию швов через изучение влияния геометрии канала на тепломассоперенос в жидкой ванне.
Методика, описанная в статьях [4; 5], может быть использована для определения геометрии канала проплавления.
Acknowledgments. This work was supported by a grant from the Russian Foundation for Basic Research RFBR 13-08-00397, 14-08-96008 and with financial support from the Russian Ministry of Education and Science at the base part of the state task (Project No 01201460538).
а

Рис. 3. Экспериментальные и рассчитанные поперечные сечения сварных швов для различных режимов фокусировки:
а - перефокусированный; 6 - острый фокус; в - недофокусированный
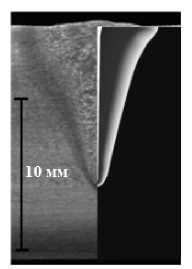
в
Список литературы Численное моделирование процесса электронно-лучевой сварки с продольной осцилляцией луча на основе экспериментально определенной формы канала проплавления
- Rai R., Palmer T. A., Elmer J. W., Debroy T. Heat transfer and fluid flow during electron beam welding of 304L stainless steel alloy, Welding Journal, March 2009, Vol. 88, No. 3, P. 54-61.
- Sudniky W., Radajz D. and Erofeew W. Computerized simulation of laser beam welding, modelling and verification, Journal of Physics D: Applied Physics, 1996, Vol. 29, No. 11, P. 2811-2817. Doi: DOI: 10.1088/0022-3727/29/11/013
- Cho W.-I., Na S.-J., Thomy C., Vollertsen F. Numerical simulation of molten pool dynamics in high power disk laser welding, Journal of Materials Processing Technology, 2012, Vol. 212, Iss. 1, p. 262-275. Doi: DOI: 10.1016/j.jmatprotec.2011.09.011
- Trushnikov D., Belenkiy V., Schavlev V., Piskunov A., Abdulin A., Mladenov G. Plasma charge current for control and monitoring at electron beam welding with the beam oscillation, Sensors, 2012, Vol. 12(12), P. 17433-17445. Doi: DOI: 10.3390/s121217433
- Trushnikov D. N., Belen’kii V. Ya. Investigation of the formation of the secondary current signal in plasma in electron beam welding with oscillations of the electron beam, Welding International, 2013, Vol. 27, Iss. 11,
- P. 877-880. Doi: DOI: 10.1080/09507116.2013.796645
- Max J. Méthodes et techniques de traitement du signal et applications aux mesures physiques, 3rd ed.; Jean-Louis Lacoume, Paris, France, 1981, Vol. I,
- P. 10-50.
- Orfanidis S. J. Optimum Signal Processing. An Introduction, 2nd ed.; Prentice-Hall: Englewood Cliffs, NY, USA, 1996, P. 5-30.
- Bachmann M., Avilov V., Gumenyuk A., Rethmeier M. Experimental and numerical investigation of an electromagnetic weld pool support system for high power laser beam welding of austenitic stainless steel, Journal of Materials Processing Technology, 2014,
- Vol. 214, Iss. 3, P. 578-591. Doi: 2013.11.013 DOI: 10.1016/j.jmatprotec
- Voller V. R., Prakash C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems, International Journal of Heat and Mass Transfer, 1987, Vol. 30, Iss. 8, P. 1709-1720. Doi: DOI: 10.1016/0017-9310(87)90317-6
- Brent A. D., Voller V. R., Reid K. J. Enthalpy-porosity technique for modeling convection-diffusion phase change: Application to the melting of a pure metal, Numerical Heat Transfer, 1988, Vol. 13, Iss. 3, P. 297-318. Doi: DOI: 10.1080/10407788808913615
- Zhang W., Kim C. H., DebRoy T. Heat and fluid flow in complex joints during gas-metal arc welding, Part I: Numerical model of fillet welding, Journal of Applied Physics, 2004, Vol. 95, Iss. 9, P. 5210-5219. Doi: DOI: 10.1063/1.1699485
- Kou S., Sun D. K. Fluid flow and weld penetration in stationary arc welds, Metalurgical Transactions A, 1985, Vol. 16, Iss. 2, P. 203-213. Doi: 10.1007/BF02815302.
- Kim C. H., Zhang W., DebRoy T. Modeling of temperature field and solidified surface profile during gas metal arc fillet welding, Journal of Physics, 2003, Vol. 94, Iss. 4, P. 2667-2679. Doi: DOI: 10.1063/1.1592012
- De A., DebRoy T. Probing unknown welding parameters from convective heat transfer calculation and multivariable optimization, Journal of Physics D: Applied Physics, 2004, Vol. 37, No. 1, P. 140-150. Doi: 10.1088/0022-3727/37/1/023.
- De A., DebRoy T. A smart model to estimate effective thermal conductivity and viscosity in weld pool, Journal of Applied Physics, 2004, Vol. 95, Iss. 9,
- P. 5230-5240. Doi: DOI: 10.1063/1.1695593


