Численное моделирование процесса течения полимера в кабельной головке и анализ зависимости параметров процесса от некоторых теплофизических свойств материала

Пермский государственный технический университет

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА ТЕЧЕНИЯ ПОЛИМЕРА В КАБЕЛЬНОЙ ГОЛОВКЕ И АНАЛИЗ ЗАВИСИМОСТИ

ПАРАМЕТРОВ ПРОЦЕССА ОТ НЕКОТОРЫХ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ МАТЕРИАЛА

В статье приведено численное решение задачи экструзии полимера и оценено влияние начальной вязкости, плотности материала и коэффициента аномалии на температурные поля.

В проводниковой продукции с полимерной изоляцией, как правило, используется не один, а несколько слоев изолирующего материала или полупроводящих экранов, необходимых для выравнивания электрического поля внутри кабеля. Формирование на токопроводящей жиле всех слоев одновременно позволяет сократить накладные расходы при производстве, а также повысить качество проводниковой продукции вследствие уменьшения количества примесей и неоднородностей между слоями изоляции.

В данной статье приведено численное решение задачи тепломассообмена в кабельной головке улучшенной конструкции, конфигурация которой позволяет реализовать безвихревое течение расплава полиэтилена, улучшающего свойства готового изделия [1, 2].

Для ряда изоляционных материалов необходимым условием качества получаемой продукции является сохранение температуры расплава полимера в диапазоне 170–180 градусов Цельсия. При превышении температуры 180 градусов происходит деструкция материала.

y

♦x

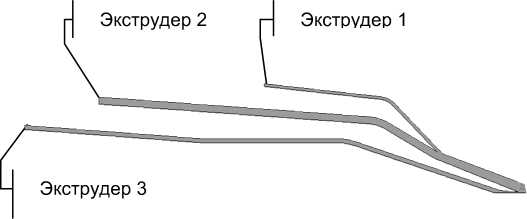
Рис. 1. Геометрия канала истечения

Для того чтобы оценить применимость геометрии канала истечения для материалов с различными реологическими и теплофизическими характеристиками, были проведены исследования зависимостей средней температуры на выходе от начальной вязкости материала (р ₀ ), плотности материала (р), показателя аномалии ( n ) и температурного коэффициента вязкости (в).

В работе были приняты следующие допущения: процесс стационарный, массовые силы пренебрежимо малы, на границах канала, образованных формующим инструментом, задаются условия прилипания и непроникновения, расплав полимера несжимаем, теплофизические характеристики постоянны. Задача рассматривалась в двумерной постановке.

Общий вид каналов истечения представлен на рис. 1.

Математическая модель основана на законах сохранения массы, количества движения и энергии [3] и представляет собой систему уравнений неразрывности (1), движения (2), энергии (3) и реологических уравнений состояния (4), дополненных граничными условиями.

dVx..'V = о, ∂x   ∂y

р (у ^dV_ ₊ у V

Р ( V дx Vy dy J

( d V_v     d V_v )

yy

P (Vх dx V dy J

dp + (dTx + dTyx' dx ( dx dy ,

dp_ + ( dTxL +dTyy' dy ( dx dy J

cρ

V_x — + V — ^x d x ^y d y J

= XA T + qv,

∂V                ∂Vy т„ = 2з —x = зг r, tw = 2з —— = зг, „, т„ = т xx 3— xx yy D-.        yy   xy     yx

= з (+ <^) = зг I dy   dx J

xy

з

₌ e -β T

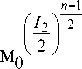
где n - эффективная вязкость, зависящая как от скорости сдвига (степенной закон), так и от температуры (уравнение Рейнольдса) (5), V_x , V_y - x и y компоненты вектора скорости, т ц ( i , j = x , y ) - компоненты тензора напряжений, y i,j ( i , j = x , y ) -компоненты тензора скоростей деформации, р - плотность полимера, T - температура, p - давление, ц ₀ - начальная вязкость, 1 ₂ - второй инвариант тензора скоростей деформации, n - показатель аномалии, в - температурный коэффициент вязкости.

В соответствии со сделанными допущениями задавались следующие граничные условия: на твердых неподвижных стенках, образованных дорном и матрицей, согласно условию прилипания и непроникновения скорости равны нулю (Vx = Vy = 0); на границе контакта с подвижной жилой скорость Vx равна линейной скорости движения жилы (Vy = 0). Скорость расплава полимера на входе каналов была рассчитана исходя из производительности каждого из трех экструдеров и задавалась в виде прямоугольной эпюры. Температура на корпусе Tк = 443 К, температура в зоне контакта с жилой определялась температурой предварительного прогрева жилы (Tж = 383 К), на входе в канал – температурой полимера на выходе из экструдеров (Tэ = 423 К). На выходе кабельной головки задавалось условие свободного истечения (давление равно атмосферному – P = 100 кПа) и граничные условия второго рода по температуре и скорости. На границах раздела потоков задавались условия равенства скорости соприкасающихся частиц и равенство векторов напряжений, действующих со стороны соприкасающихся потоков.

Реологические и теплофизические характеристики материала, использовавшиеся при расчете, представлены в таблице.

Свойства материала

Плотность, кг / м 3	550–900
Вязкость, Па / c	7000–13000
Коэффициент аномалии	0,1–0,7
Теплоемкость, Дж / кг·К	2500
Теплопроводность Вт / м·К	0,182
Температурный коэффициент вязкости β, 1 / K	0,007

Задача течения и теплообмена расплава материала решалась численно при помощи метода конечных элементов с использованием среды инженерных расчетов ANSYS с библиотекой FLOTRAN CFD и h -метода решения [4]. Для разбиения модели на конечные элементы был использован элемент FLUID141, позволяющий рассчитывать поля скоростей, температур и давления в заданной области и оперирующий такими свойствами материала, как плотность, вязкость, теплоемкость и теплопроводность. Всего было порядка 20 тысяч узлов и 18 тысяч элементов. Часть сетки разбиения модели представлена на рис. 2.

В результате решения поставленной задачи были получены поля температур, скоростей, вязкости и давления.

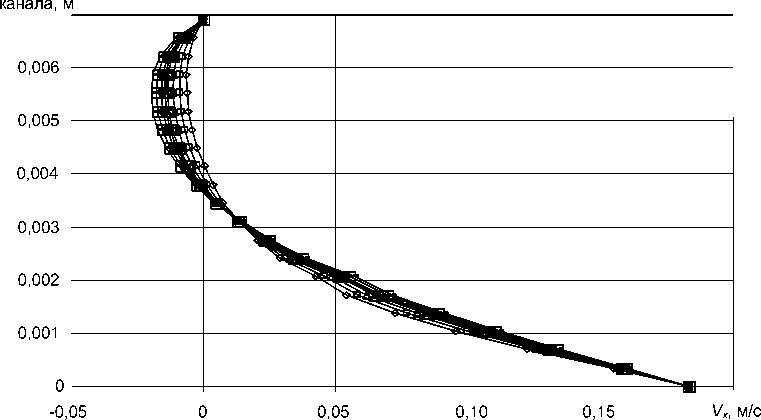
На рис. 3 приведена зависимость продольной компоненты скорости V x от коэффициента аномалии вязкости n . При увеличении n в семь раз (от 0,1 до 0,7) увеличивался противоток расплава полимера, что приводило к незначительному уменьшению расхода.

Высота

|-«--0,1                -и- - 0,4                1- - 0,6

-^-0,2            ^—0,44            __-0,7

-*— 0,3              -^ 0,5

Рис. 3. Распределения V x , на выходе для различных n

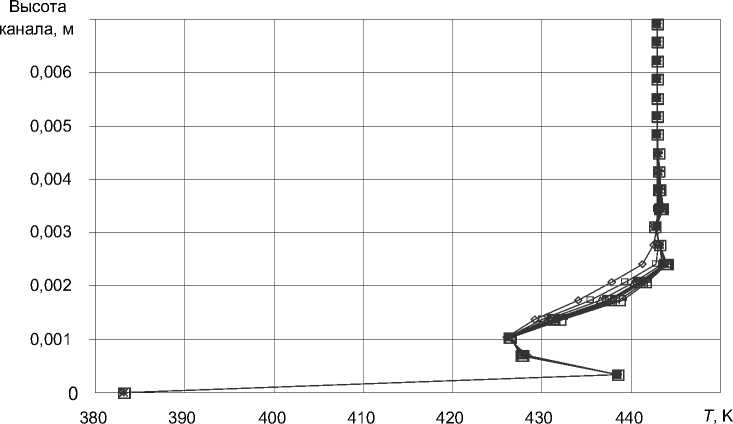
Изменение температуры в нижней части потока экструдера 2 при изменении коэффициента аномалии вязкости не превышало 4˚С (рис. 4).

|-«--0,1                -и- - 0,4                1- - 0,6

-^-0,2            ^—0,44            __-0,7

-*— 0,3              -^ 0,5

Рис. 4. Распределения температуры T на выходе для различных n

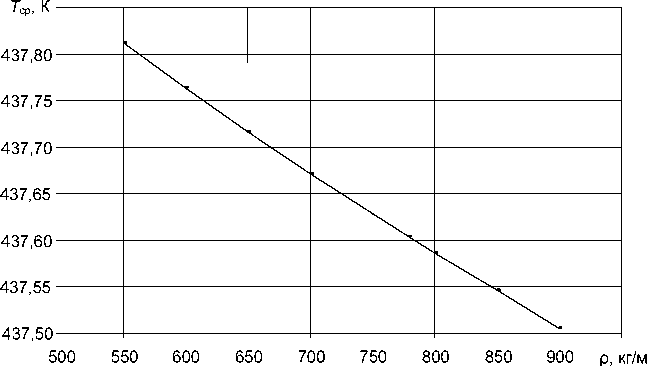
Рис. 5. Зависимость средней температуры на выходе Т ср от плотности материала ρ

На рис. 5 показана зависимость средней температуры на выходе из канала от плотности материала (ρ). Увеличение плотности от 550 до 900 кг/м ³ приводило к уменьшению средней температуры на выходе расчетной области. Максимальная разница средней температуры при этом составила порядка 0,3 градуса.

Увеличение начальной вязкости (µ 0 ) в диапазоне от 7000 до 9000 Па/с приводило к увеличению средней температуры на выходе, а при дальнейшем увеличении вязкости от 9000 до 13000 Па/с средняя температура не меняется (рис. 6). Однако, учитывая диапазон изменения средней температуры (0,05 градуса), зависимостью средней температуры от начальной вязкости можно пренебречь.

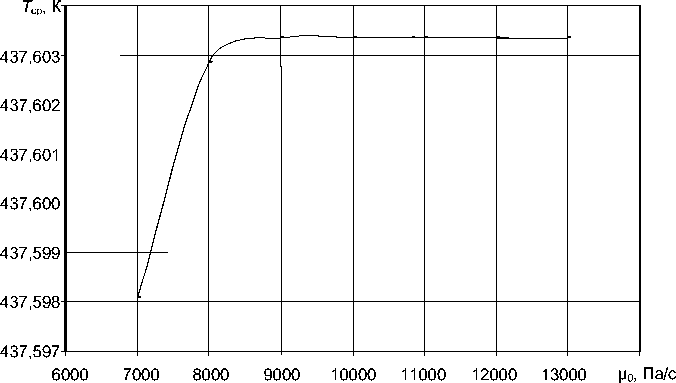
Рис. 6. Зависимость средней температуры на выходе Т ср от вязкости µ 0

На рис. 7 представлена зависимость средней температуры на выходе от коэффициента аномалии ( n ). При увеличении n в семь раз (от 0,1 до 0,7) средняя температура на выходе возросла на 0,8 градуса.

Изменение температурного коэффициента вязкости β от 0,001 до 0,013 выявило увеличение средней температуры на выходе (рис.8) на 0,35 градуса.

Таким образом, исследование показало, что наиболее существенное влияние на процесс тепломассообмена оказывает величина коэффициента аномалии вязкости n .

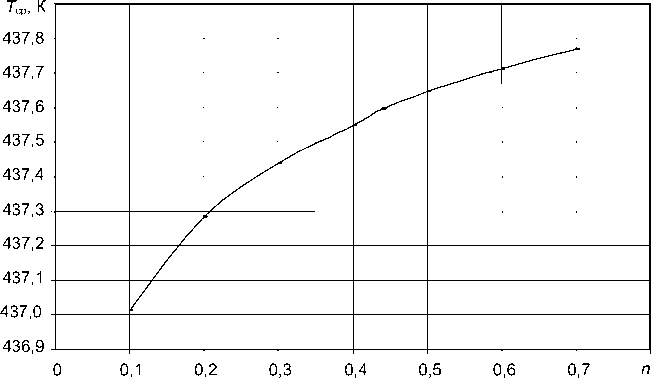
Рис. 7. Зависимость средней температуры на выходе Тср от показателя аномалии n

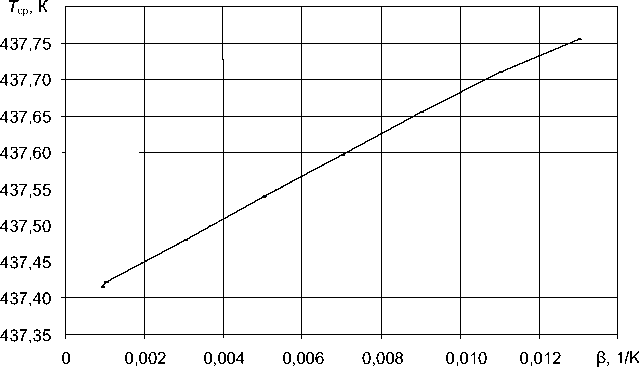
Рис. 8. Зависимость средней температуры на выходе Тср от температурного коэффициента вязкости β

Поскольку во всех случаях средняя температура на выходе менялась незначительно (максимальный перепад не превышает один градус), можно сделать вывод о целесообразности использования предложенной ранее геометрии не только для исследуемого материала (сшиваемый полиэтилен низкой плотности), но и для материалов с характеристиками, отличающимися от заданных.