Численное моделирование процесса теплопередачи в радиационно-конвективном размораживающем устройстве

ющегося перегрузкой угля. Технологическая схема разгрузки топлива состоит из следующих операций:

• a)    приход топлива в полувагонах на территорию терминала;

• b)    маневровые работы для постановки полувагонов на разогрев;

• c)    разогрев топлива в вагоноразмораживающих устройствах (далее тепляках);

• d)    маневровые работы для постановки полувагонов в вагоноопрокидыватель;

• e)    разгрузка вагонов в вагоноопрокидывателе;

• f)    маневровые работы по уходу вагонов с территории терминала.

Пункты b и c выполняются только в холодный период времени года (ориентировочно с октября по март).

Проблемы с разгрузкой появляются в зимний период, так как большую часть в технологической цепочке разгрузки начинает играть разогрев угля. В зимнее время продолжительность разогрева угля в размораживающих устройствах составляет до 50 % от всех операций. Совершенствование конструкции размораживающего устройства становится актуальным, так как позволяет существенно уменьшить общее время разгрузки угля в зимний период.

Одним из основных условий при работе размораживающих устройств, помимо разогрева груза, является поддержание таких условий, в которых бы не возникала опасность повреждения элементов вагонов от воздействия температуры. Сотрудниками кафедры теплоэнергетики и теплотехники ДВФУ совместно с персоналом ОАО «Восточный порт» проведены тепловые испытания размораживающих устройств № 1÷4 [1, 2]. Одной из задач при проведении испытаний было определение безопасных режимов работы размораживающего устройства, в которых отсутствует перегрев элементов вагонов выше допустимой температуры.

В результате проведенных тепловых испытаний получены скорости нагрева угля и отдельных элементов вагона. При сопоставлении полученных скоростей нагрева с предельной температурой, при которой допускается нормальная эксплуатация этих элементов, установ-ленно «безопасное» время разогрева угля, при котором не происходит перегрева отдельных элементов (рис. 1).

При расчете выбиралась максимальная скорость нагрева и начальная температура вагона минус 20 °C. Полученное наименьшее «безопасное» время разогрева для металлической

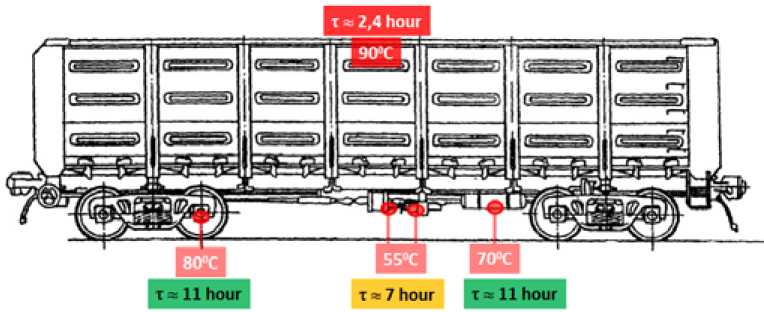
Рис. 1. Безопасное время при разогреве угля в размораживающем устройстве стенки вагона в несколько раз меньше, чем для остальных элементов вагона (тормозное оборудование, подшипники и т.д.). Можно сделать вывод, что ограничивающим фактором при разогреве вагонов с углем будет являться температурное состояние стенки вагона в верхней части. Результаты экспериментальных исследований позволяют оценить скорость нагрева угля и элементов вагона. Сопоставление различных режимов работы размораживающего устройства представляет определенные сложности в связи с большим количеством параметров, не поддающихся контролю в эксплуатационных условиях, таких как температура наружного воздуха, начальная температура груза, свойства угля. Для решения вышеперечисленных проблем необходимо выполнить численное моделирование процесса теплообмена при разогреве угля в размораживающем устройстве.

Моделирование теплообмена в размораживающем устройстве

Расчетная схема приведена на рис. 2. Задача решалась в двухмерной постановке. В области Ω1, характеризующей массив угля, решается уравнение теплопроводности [3]. В области Ω2 (воздух в размораживающем устройстве) решается система уравнений для естественной тепловой конвекции в приближении Буссинеска [4]. Область Ω3 характеризует металлическую стенку вагона, в этой области решается уравнение теплопроводности. Область Ω4 и Ω5 характеризует металлическое колесо вагона и его наполнение смазочным материалом (полое колесо), в этих областях решается уравнение теплопроводности.

На границах 1, 2, 3 задаются граничные условия 1-го рода, характеризующие температуру нагревательных элементов – паровых регистров tг, °C. На границе 4 задаются адиабатные условия, без теплообмена. На границе 5 задаются граничные условия 1-го рода, характеризующие

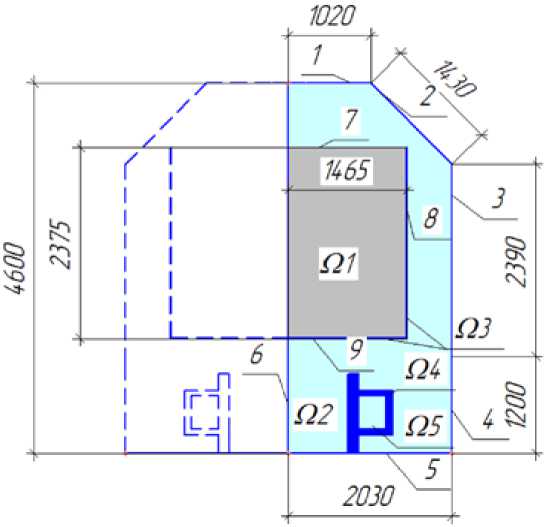
Рис. 2. Расчетная схема при моделировании процесса разогрева угля в вагоне температуру поверхности tпов, °C. На границе 6 задаются условия симметрии расчетной области, т.е. граница 6 является осью симметрии для указанной расчетной области. На границе 7, 8, 9 задаются граничные условия 4-го рода. На границе областей Ω2 и Ω4, Ω4 и Ω5 задаются граничные условия 4-го рода.

При расчете учитывалось тепловое излучение между поверхностями 1, 2, 3, 7, 8, 9 и внешними поверхностями области Ω4 [5]. Воздух принят как прозрачная среда, не поглощающая излучение. Степень черноты всех поверхностей, участвующих в теплообмене излучением, принята одинаковой и равной 0,8.

Параметры для воздуха (плотность, теплоемкость и вязкость) рассчитывали как для идеального газа и учитывали зависимость от температуры [6]. Металлическая стенка вагона и колесо (области Ω3, Ω4) имели следующие параметры: плотность 7850 кг/м3, теплоемкость 475 Дж/(кг*К), коэффициент теплопроводности 44,5 Вт/(м*К) [7]. Смазочный материал области Ω5 задавался следующими величинами: плотность 903 кг/м3, теплоемкость 1980 Дж/(кг*К), коэффициент теплопроводности 0,135 Вт/(м*К) [8]. Уголь рассчитывался как однородная изотропная среда с заданными теплофизическими свойствами [9]. Начальные условия для всех областей (Ω1, Ω2, Ω3, Ω4, Ω5) заданы одинаковыми и равными начальной температуре угля t 0 , °C.

Режим течения воздуха возле нагретых тел, вызванный естественной конвекцией, может быть как ламинарным, так и турбулентным. Для определения режима течения необходимо знать число Рэлея, для выбранных начальных условий получено значение числа Рэлея Ra ≈ 1,3 · 1011. По данным работы [10], развитое турбулентное течение наступает при числах Ra≥6 · 106.

В качестве замыкающей модели турбулентности использовалась стандартная k-ε модель [11] с константами замыкания: Cm=0,09; Sk=1,0; Se=1,3; С1=1,44; C2=1,92. В расчетной области была построена неравномерная сетка с использованием треугольных элементов с пятью тетраэдральными слоями в пристенной области для разрешения пограничного слоя. Решение производилось методом конечных элементов с использованием программного комплекса ANSYS.

Результаты численного моделирования

Для проверки представительности разработанной модели выполнено сопоставление расчетных данных с результатами эксперимента. В качестве критериев сопоставления выбраны следующие параметры. Первый параметр – это температура воздуха внутри тепляка на разных высотах с течением времени (рис. 3 а ). Точками на графике показаны данные эксперимента, линиями – результаты расчета. Данный параметр характеризует температурное поле по высоте размораживающего устройства; если расчетные данные имеют совпадение с экспериментом, это свидетельствует о хорошей сходимости численного решения модели переноса теплоты за счет конвекции. Второй параметр – температура угля, совпадение говорит об адекватном описании процесса распространения теплоты внутри массива угля за счет теплопроводности (рис. 3 b ). По результатам сопоставления можно сделать вывод о хорошей сходимости результатов численного моделирования. Разработанная модель может использоваться для исследования влияния режимных характеристик работы размораживающего устройства на процесс разогрева угля в вагонах.

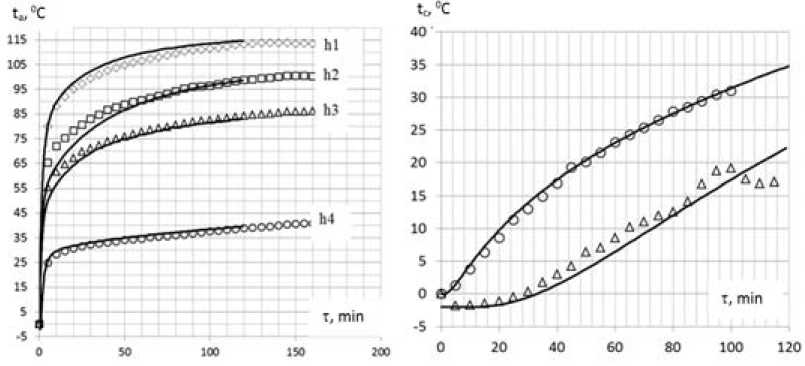
а) температура воздуха по высоте

b) температура угля

Рис. 3. Сопоставления расчетных и экспериментальных зависимостей

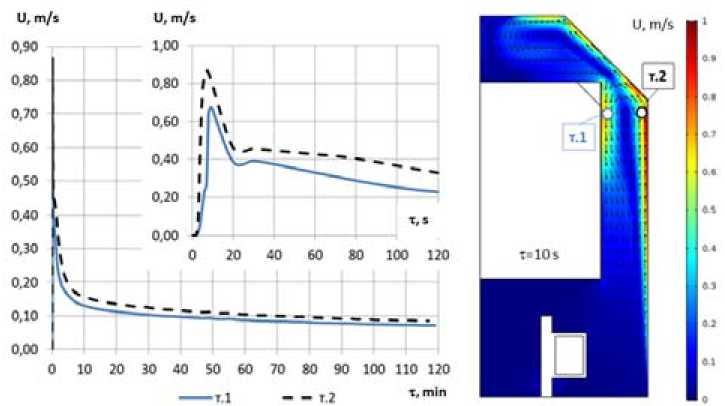
Рис. 4. Скорость движения воздуха в характерных точках

В результате моделирования получено поле скоростей (рис. 4) внутри размораживающего устройства. Интенсивное движение воздуха внутри размораживающего устройства, вызванное разностью плотностей за счет нагрева, имеет очень непродолжительный промежуток времени. Максимальные скорости достигаются для времени τ=10 с и составляют около 0,9 м/с. Потом скорости заметно снижаются. Области воздуха, в которых наблюдается максимальные скорости (до 0,9 м/с) составляют небольшую долю от общего объема воздуха. После τ=20 мин движение воздуха внутри размораживающего устройства практически останавливается. Это свидетельствует о том, что конвективный перенос теплоты имеется только на начальном этапе. В дальнейшем основной перенос теплоты осуществляется за счет теплопроводности и излучения.

Для снижения времени разогрева угля при сохранении безопасных условий для вагона предлагается проводить разогрев при переменной температуре нагревательных элементов. В начальный момент времени нагрев следует вести с максимально возможной температурой, а по мере нагрева стенки вагона до опасного значения – снижать температуру нагревательных элементов до безопасного значения. В результате теплота, полученная в начальный момент времени при больших градиентах температуры, позволит сократить общее время нагрева. Вариант с непрерывно изменяющейся температурой будет давать максимальное снижение времени, но такой вариант сложно реализуем на практике. Дискретное же изменение температуры реализуется легко. Вагон устанавливается в размораживающее устройство, давление пара в нагревательных элементах поднимается до максимально возможного. Через определенное время (это время вычисляется при моделировании) давление пара снижается до безопасного и вагон выдерживается в оставшееся время до полного разогрева угля. Для решения данной задачи необходимо задаться предельным давлением пара в нагревательных элементах. Эксплуатационное давление в размораживающих установках не превышает давления Рп=0,6 МПа. Технически на размораживающее устройство можно подать давление пара с величиной Рп=1,3 МПа, так как котлы, являющиеся источником пара, имеют номинальное давление пара в барабане Рб=1,4 МПа. Эти два давления (Рп=0,6 МПа и Рп=1,3 МПа) заложены при оптимизации режимов, как лимитирующие факторы по температуре нагревательных элементов. Сопоставление производилось с исходным режимом, при котором температура пара в нагревательных элементах не изменяется. Для такого режима безопасное давление пара в нагревательных элементах составило Рп=0,32 МПа, а время разогрева угля τ=108 мин. Режим 1 соответствует начальному давлению пара Рп=0,6 МПа, режим 2 – начальному давлению Рп=1,3 МПа. На рис. 5 приведены результаты расчета для исходного режима и двух режимов с переменной температурой нагревательных элементов.

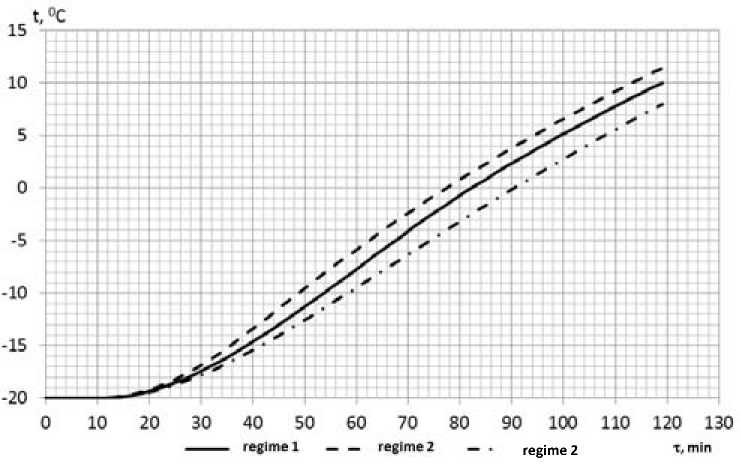
Рис. 5. Нагрев угля при режимах с переменной температурой

В режиме 1 при Рп=0,6 МПа и температуре пара в нагревательных элементах t нас =162,0 °C производился разогрев вагонов в течение 55 мин с дальнейшим понижением температуры пара в нагревательных элементах до t_нас=127,4 °C, что соответствует давлению Рп=0,25 МПа. В режиме 2 давление пара составило Рп=1,3 МПа, температура пара в нагревательных элементах t_нас=191,6 °C. Производился разогрев вагонов в течение 30 мин с дальнейшим понижением температуры пара в нагревательных элементах до t нас =133,5 °C, что соответствует давлению Рп=0,3 МПа. При заданных режимах нагрев угля происходил быстрее, чем стенка вагона перегревалась относительно заданной температуры (90 °C). Снижение времени разогрева угля по сравнению с исходным режимом с постоянной температурой нагревательных элементов составил: для режима 1 – 8,5 мин или 7,9 %, для режима 2 – 13,7 мин или 12,7 %.

Заключение

В результате исследования получены скорости нагрева угля и различных элементов вагона в процессе разогрева в размораживающих устройствах.

Воздействию наиболее высоких температур подвергаются стенки вагона в верхней части. Время пребывания вагонов в тепляке будет ограничивать именно эта деталь вагона.

В результате численного моделирования получена картина переноса теплоты при разогреве. Выявлено, что наиболее интенсивная свободная конвекция наблюдается в течение непродолжительного времени, около 20 мин. Дальнейший процесс переноса теплоты идет в основном за счет теплопроводности и излучения.

Применение режима работы размораживающего устройства с переменной температурой нагревательных элементов позволяет получить экономию времени при разогреве угля на величину от 87,9 до 12,7 %.