Численное моделирование процессов взаимовлияния волны возмущения в водороде и перегородки в модельном канале

ВЕСТНИК ПНИПУ. МЕХАНИКА № 6, 2023PNRPU MECHANICS BULLETIN

Одним из приоритетных направлений развития энергетики в Российской Федерации, согласно энергетической стратегии ЭС-2035, выступает транспортировка и хранение водорода и водородосодержащих газовых смесей как для внутреннего потребления, так и для экспорта [1–10].

На сегодняшний день основным способом транспортировки водорода и водородосодержащих смесей являются существующие трубопроводы природного газа, зачастую изготовленные из стали. Однако при эксплуатации таких трубопроводов имеют место существенные проблемы:

– потери объема водорода из системы превышают более чем в 3 раза, чем таковые природного газа;

– повышенный шум, возникающий при транспортировке водорода и водородосодержащих газовых смесей, на газораспределительных станциях (ГРС). Действующие нормы для помещений ГРС, установленные в 85 ДБ, предъявляются и к транспортировке водорода.

Проблема шума, или акустических процессов, становится наиболее актуальной с учетом прогнозов по развитию отрасли. Так, к 2040 г. прогнозируется система трубопроводов для транспортировки водорода протяженностью более 23 тыс. км, из которых 75 % будут составлять переоборудованные действующие магистрали для транспортировки природного газа [11; 12]. В связи с этим в работе затрагиваются вопросы, связанные с шумом, возникающим при транспортировке водорода. Так, рассматриваются процессы, связанные с возникновением, распространением акустической волны в трубопроводе в условиях транспортировки водорода.

Моделирование акустических процессов зачастую связано с источниками их возникновения и распространения в моделируемой рабочей среде. Необходимо определить акустические характеристики на установке «канал с потоком» [13–28]. При этом не учитывается возникновение возможных резонансных явлений и/или процессов ослабления акустических волн в динамической системе «газ – конструкция». Для возможности учета данных процессов необходимо рассматривать краевую задачу в полной постановке, как 2 FSI -связанную задачу взаимовлияния деформируемой конструкции и газодинамического потока (англ. 2-way FluidStructure Interaction), т.е. в аэроупругой постановке, как, например, было сделано в работах [29; 30]. Примеров исследований акустических процессов в 2 FSI -постановке недостаточно. На данный момент подобные исследования в связанной постановке задачи имеют отражения в работах таких авторов, как Р.В. Мормуль и А.С. Голдобин, В.Я. Модорский, А.О. Микрюков, А.Е. Кирюшкин, Л.Л. Миньков, И.К. Марчевский, В.В. Лукин, Ф.С. Кулешов и др. [31–35]

В данной работе моделируются акустические процессы в трубопроводе при транспортировке водорода с использованием 2FSI-подхода. Исследования направлены на выявление закономерностей по распростра- нению и гашению звуковой волны в модельном приближении трубопровода. В качестве модельного приближения рассматривается канал прямоугольного сечения, разделенный одной или несколькими перегородками, жестко защемленными по периметру.

В качестве материала перегородки рассматриваются несколько вариантов, существенно различающихся по физико-механическим характеристикам: сталь, титан, полиэтилен и стеклопластик. При интенсивном воздействии водорода на перегородке появляются деформации и возможно возникновение процессов поврежденности и/или разрушения, что может также сказаться на поведении акустического поля. Данные процессы также требуют дополнительного изучения.

В качестве рассматриваемых рабочих тел используются воздух или чистый водород.

Таким образом, исследования направлены на оценку влияния физико-механических характеристик конструкции перегородки на распространение и гашение акустических волн в воздухе/водороде внутри модельного канала прямоугольного сечения.

1.    Постановка задачи моделирования акустических процессов в модельном канале

В работе исследуются два варианта конструкции: с одной и двумя перегородками.

Вначале рассмотрен вариант геометрии канала прямоугольного сечения с одной установленной перегородкой. Расположение областей задания начальных и граничных условий, контрольных точек измерений представлено на рис. 1. Канал прямоугольного сечения составляет 50 × 100 × 800 мм. Перегородка толщиной 1 мм делит длину канала пополам.

Для оценки влияния материала перегородки на процессы распространения и гашения акустической волны в канале квадратного сечения выбраны контрольные точки:

• –    т. 1, 2 располагаются до перегородки (со стороны возникающих возмущений потока), т. 1 – вблизи генератора колебаний справа, т. 2 – посредине левой полости;

• –    т. 3 располагается в непосредственной близости от перегородки слева по рисунку;

• –    т. 4 располагается в непосредственной близости от перегородки справа по рисунку;

• –    т. 5, 6 располагаются после перегородки, т. 5 – посредине правой полости, т. 6 – вблизи заглушки слева;

• –    т. 7 располагается внутри перегородки, по центру, для возможности оценки ее перемещений.

Математическая модель связанной 2 FSI -постановки для обозначенной рабочей области базируется на методе расщепления по физическим областям: газодинамической и механической.

Для газодинамической области сформулирована следующая концептуальная постановка:

• 1.    Исследуемые процессы рассматриваются в трехмерной нестационарной постановке.

• 2.    Объектами исследования являются два рабочих тела: воздух или чистый водород. Рабочие тела обладают постоянством состава с заданными свойствами.

• 3.    В начальный момент времени рабочее тело не имеет возмущений физических параметров.

• 4.    Для исследуемых рабочих тел не рассматриваются возможные химические процессы.

• 5.    Рабочее тело рассматривается в приближении од-нофазности потока.

• 6.    Канал заполнен рабочим телом до и после перегородки.

• 7.    Стенки канала рассматриваются как недеформи-руемые, процессы теплопередачи не учитываются.

• 8.    Для исследуемых процессов не учитывается влияние гравитации.

• 9.    Источником возмущения является внешнее воздействие, описываемое одномодовым синусоидальным сигналом.

• 10.    Рабочее тело влияет на перегородку как процесс перераспределения газодинамических полей потока и в то же время является откликом на процесс деформирования перегородки; при этом генерируемая на входе волна распространяется по длине канала, достигает перегородки, сталкивается с ней, отражается, частично гасится и проникает через перегородку с последующей трансляцией возмущений в поток.

Для механической области (перегородка в канале прямоугольного сечения) сформулирована следующая концептуальная постановка:

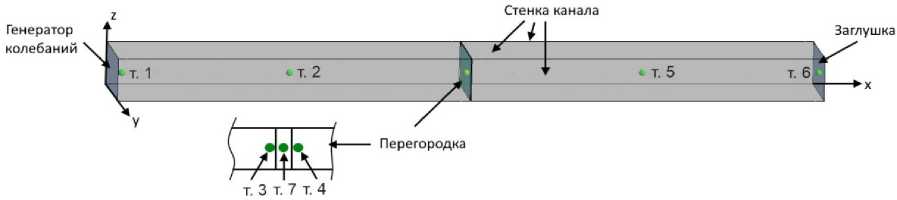
Рис. 1. Схема модельной геометрии канала с перегородкой и расположением областей для задания граничных условий

Fig. 1. Scheme of the model channel geometry with a barrier and the location of areas for specifying boundary conditions

• 1.    Процессы в перегородке описываются в линейном приближении теории упругости и рассматриваются в трехмерной нестационарной постановке.

• 2.    В начальный момент времени перегородка не деформирована.

• 3.    Перегородка размещается внутри канала и имеет защемление (жесткая заделка) по периметру.

• 4.    Под влиянием возмущений от газодинамического потока перегородка деформируется, при этом рассеивая волну, с последующим распространением остаточного возмущения в потоке по другую сторону перегородки.

• 5.    На поверхностях перегородки, взаимодействующих с газодинамическими областями, выполняются условия совместности воздействий.

Таким образом, разработанная математическая модель связанной 2 FSI -постановки для исследуемых акустических процессов в канале прямоугольного сечения с перегородкой базируется для газодинамической области на уравнениях Рейнольдса, замкнутых моделью турбулентности k -ω (англ. Shear-Stress Transform), позволяющей разрешать распространение акустической волны по потоку. Для механической области описывается дифференциальными уравнениями в перемещениях в приближении линейной изотропной теории упругости. Полная система уравнений математической модели исследуемых процессов представлена в работе коллектива авторов [36]. В работе [36] приведены результаты подобных исследований, полученных для рабочей среды – воздух. Данные результаты используются для последующего сравнительного анализа.

Для численной реализации в работе использовался программный комплекс инженерного анализа ANSYS , позволяющий моделировать исследуемые процессы в рамках разработанной 2 FSI -математической модели.

В качестве начальных условий для газодинамических областей задана величина давления, соответствующая 0,1 МПа.

Граничные условия расчетной области (см. рис. 1) определены на соответствующих областях следующим образом:

• –    поверхность «Генератор возмущений» соответствует подвижной стенке, движущейся по синусоидальному закону. В терминах перемещений это соответствует зависимости U = 10 sin(2π 50t), частота колебаний 50 Гц;

• –    на поверхности «Перегородка» определены условия типа деформируемая стенка, с возможностью восприятия воздействий от набегающий акустической волны;

• –    на поверхностях «Заглушка» и «Стенка канала» определены условия типа неподвижная стенка, без прилипания потока, отсутствует шероховатость.

2.    Моделирование акустических процессов для модели канала с одной перегородкой

Для расчетной схемы разработаны сеточные модели соответствующих областей в рамках топологии O-grid .

Были проведены вычислительные эксперименты для трех вариантов материала перегородки: из стали (модуль упругости Е = 2^10¹¹ Па), из титана ( Е = 1,12^10¹¹ Па) и полиэтилена ( Е = 1,1^10⁹ Па). Моделируемый отрезок времени соответствует 50 мс.

По результатам вычислительных экспериментов, проиллюстрированных на рис. 2, получены зависимости амплитуды перемещений перегородки от времени для исследуемых материалов в условиях воздуха и чистого водорода. Стоит отметить, что результаты, полученные для перегородки из полиэтилена, для воздуха и чистого водорода на диаграмме (см. рис. 2) построены по вспомогательной оси ординат, расположенной справа на рисунке.

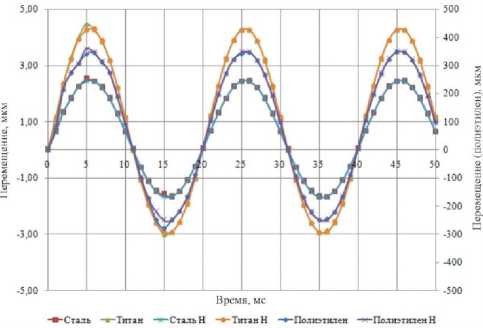
Рис. 2. Диаграммы зависимости перемещений точки 7 от времени при различных материалах перегородки при воздействии воздуха (сталь, титан, полиэтилен) и чистого водорода (сталь H, титан H, полиэтилен H)

Fig. 2. Diagrams of the dependence displacements (point 7) on time for various barrier materials when exposed to air (steel, titanium, polyethylene) and pure hydrogen (steel H, titanium H, polyethylene H)

При анализе результатов выявлено, что амплитуда колебаний перегородки обратно пропорциональна модулю упругости применяемого материала. Так, применение полиэтилена (модуль упругости Е = 1,1^10⁹ Па) вместо стали (модуль упругости Е = 2^10¹¹ Па) приводит к двукратному увеличению амплитуды колебаний. Эта зависимость прослеживается как в воздушной рабочей среде, так и в водороде.

С другой стороны, колебания перегородки имеют несимметричный характер как в пространстве, так и во времени. То есть перемещения перегородки в направлении распространения возмущения в потоке имеют большие значения, чем в противоположном направлении. Продолжительность полупериодов колебаний перегородки также неодинакова. При движении в направлении распространения возмущения в потоке полупериод больше, чем в противоположном направлении.

По результатам вычислительных (см. рис. 2) экспериментов на интервале от 0 до 7 мс наблюдается нелинейность как по перемещениям перегородки, так и по распределению параметров потока в водородной среде.

Анализ зависимости разности давлений в исследуемых рабочих средах в контрольной точке 3 (рис. 3) от времени показал, что максимум наблюдается в момент прохождения перегородкой положения равновесия в конце полупериода колебаний. Разность давлений Δ P определена как разность давления в водороде и воздухе (Δ P = P H 2 - P air ).

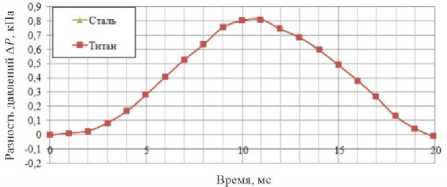
Рис. 3. Диаграммы зависимости разности давлений между воздухом и водородом от времени при различных материалах перегородки (сталь, титан) в контрольной точке 3

Fig. 3. Diagrams of the pressure difference between air and hydrogen versus time for different barrier materials (steel, titanium) at control point 3

В соответствии с результатами, проиллюстрированными на рис. 3, существенных различий в характере изменения параметров потока при использовании различных материалов перегородки не обнаружено. Разность давлений Δ P имеет гармонический характер изменения.

Проведен сравнительный анализ перемещений перегородок из стали, титана и полиэтилена при воздействии волны в воздухе и волны в водородной среде, проиллюстрированный на рис. 4. Результаты приведены (см. рис. 4) в виде разности перемещений Δ U x ,

ΔUx = UH2 – Uair, где UH2 – перемещение в перегородке в направлении оси X при воздействии водорода; Uair – перемещение в перегородке в направлении оси X при воздействии воздуха.

На рис. 4 на вспомогательной, правой, оси ординат приведены результаты для полиэтилена.

Выявлена корреляция между рабочей средой и поведением перегородки при заданном законе возмущения рабочего тела. Так, при воздействии волны водорода на перегородку из полиэтилена наблюдаются бо́ льшие значения перемещений, чем на воздухе, с учетом знака перемещений.

Минимальные амплитуды зависимости Δ U x обнаружены для стальной перегородки, максимальные – для полиэтилена. Зависимости напоминают гармонические и соответствуют движению контрольной точки 7. При этом Δ U x меняет знак при смене направления перемещения перегородки со смещением узловой точки вправо по временной оси. Полупериод перемещений по потоку больше полупериода перемещений против потока в 1,22 раза и слабо зависит от рассматриваемого материала.

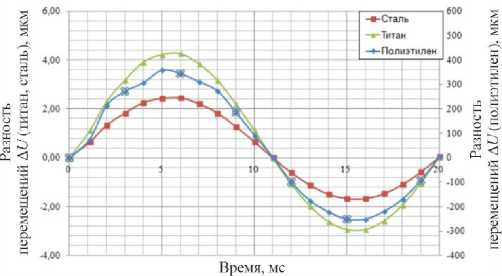
Рис. 4. Диаграммы зависимости разности перемещений перегородки при взаимодействии с воздухом или водородом от времени при различных материалах перегородки (сталь, титан, полиэтилен) в точке 7

Fig. 4. Diagrams of the difference in displacement of the barrier when interacting air or hydrogen versus time for different barrier materials (steel, titanium, polyethylene) at point 7

На рис. 5 приводятся одновременно изменения перемещений во времени для перегородки из полиэтилена в точке 7 (правая ось ординат на рис. 5) и изменения давления во времени в точке 3, расположенной слева вблизи точки 7 в газодинамической полости (левая ось ординат на рис. 5).

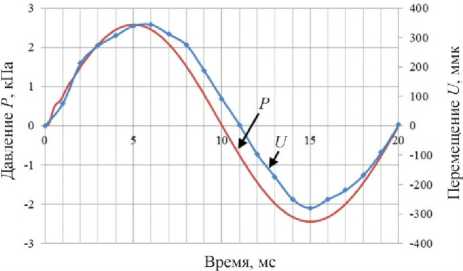
Рис. 5. Диаграммы зависимости давления и перемещений перегородки из полиэтилена в рабочей среде (воздух) от времени

Fig. 5. Diagrams of pressure and displacement of a polyethylene barrier in the air versus time

По результатам наблюдаются запаздывание перемещений перегородки примерно на π/20 относительно колебаний давления в воздухе. Особенно этот эффект выражен при прохождении перегородки положения равновесия.

На рис. 6 и 7 показаны зависимости изменения давления и перемещений перегородки из титана и стали в тех же контрольных точках, что и на рис. 5. Рабочее тело – воздух. Отставание перегородки примерно на π/20, что и для перегородки из полиэтилена.

Для титановой и стальной перегородок график изменения давления во времени имеет близкие (по модулю) амплитуды как при движении перегородки вправо, так и влево. Графики перемещений имеют существенные отличия от гармонических зависимостей. Амплитуда перемещений перегородки вправо значительно больше (в направлении распространения волны в рабочей среде), а против движения волны – меньше. На титане и стали это отличие достигает 1,5 раза. На полиэтилене отличие составляет 1,25 раза.

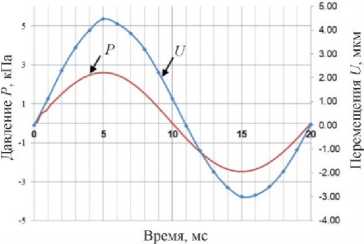
Рис. 6. Диаграммы зависимости давления и перемещений перегородки из титана в рабочей среде (воздух) от времени

Fig. 6. Diagrams of pressure and displacement of a titanium barrier in the air versus time

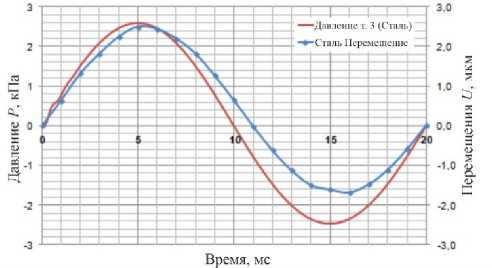
Рис. 7. Диаграмма зависимости давления (т. 3) и перемещений (т. 7) для перегородки из стали в рабочей среде (воздух) от времени

Fig. 7. Diagrams dependence of pressure and displacement of a steel barrier at the air versus time

3.    Моделирование акустических процессов для модели канала с двумя перегородками

Представляет интерес анализ влияния второй перегородки, изготовленной из того же материала и установленной в канал на некотором расстоянии за первой.

На рис. 8 показана модельная труба с дополнительной перегородкой. Расстояние между перегородками составляет 20 мм. Газодинамические полости заполнены воздухом или водородом.

Концептуальная и математическая постановка доопределены условиями взаимовлияния между перегородкой 2 и газом аналогично модели с одной перегородкой. Начальные и граничные условия для исследуемого варианта конструкции соответствуют варианту с одной установленной перегородкой.

В качестве исследуемого материала перегородок рассматривался стеклопластик с модулем упругости Е = 22 ГПа. По результатам вычислительного эксперимента с двумя перегородками получены зависимости изменения давления рабочего тела от времени в контрольных точках и зависимости перемещения геометрических центров перегородок от времени.

Были проведены вычислительные эксперименты для рассматриваемой конфигурации прямоугольного канала. Моделируемый отрезок времени соответствует 50 мс.

По результатам вычислительных экспериментов, проиллюстрированных на рис. 9, получены зависимости амплитуды перемещений перегородок из стеклопластика от времени в условиях водорода. Стоит отметить, что перемещения, полученные для второй перегородки, на диаграмме (см. рис. 9) обозначены U 2 и построены на правой вспомогательной оси ординат. Перемещения, полученные для первой перегородки, на диаграмме (см. рис. 9) обозначены U 1 и построены на левой основной оси ординат.

Из анализа результатов, приведенных на рис. 9, следует, что характер колебаний перегородки 2 по средним значениям совпадает с формой колебаний перегородки 1. Но при движении перегородки 2 в направлении волны возмущения в газе происходит модулирование колебаний с частотой, соответствующей собственной частоте перегородок. Этого не наблюдается на перегородке 1. При движении перегородки 2, как и перегородки 1, в направлении волны возмущения в газе колебания модулируются частотой, соответствующей собственной частоте больших газодинамических полостей. Затем эти процессы затухают. Колебания перегородки 2 на два порядка ниже, чем для перегородки 1.

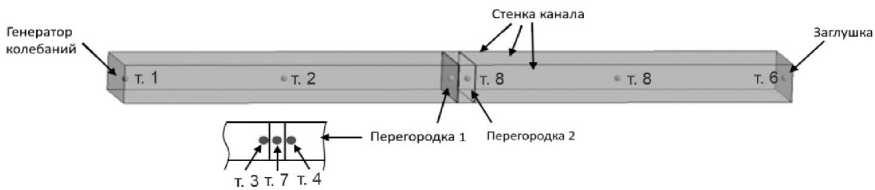
Рис. 8. Схема модельной геометрии канала с перегородками и расположением областей для задания граничных условий

Fig. 8. Scheme of the model channel geometry with two barriers and the location of areas for specifying boundary conditions

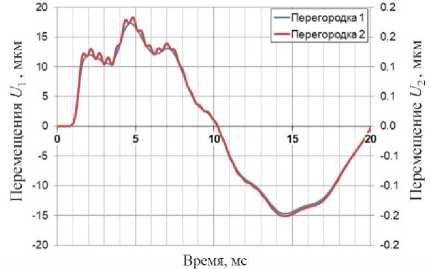
Рис. 9. Диаграмма зависимости перемещений первой и второй перегородки от времени на водороде

Fig. 9. Diagram of the displacements of the first and second barrier versus time on hydrogen

На рис. 10 проиллюстрированы результаты по изменению величины давления и перемещений первой перегородки в рассматриваемой конфигурации от времени.

Введение второй перегородки меняет характер колебаний как по перемещениям перегородки 1, так и по изменению давления вблизи нее, по сравнению с конструкцией, имеющей только одну перегородку в прямоугольном канале (см. рис. 5–7). В этом случае наблюдаются не только колебания на несущей частоте 50 Гц, но и их модуляция на собственной частоте газодинамической полости ( L = 400 мм).

Асимметрия колебаний наблюдается как в газе, так и в конструкции. Если на одной перегородке снижение давления P на втором полупериоде не наблюдалось, то при наличии второй перегородки давление во втором полупериоде уменьшается.

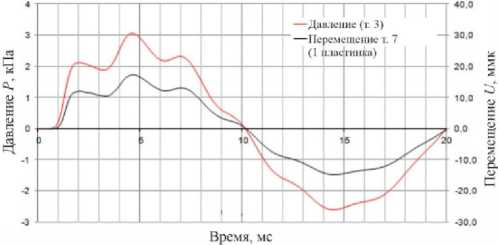
Рис. 10. Диаграмма зависимости изменения давления в водороде (точки 3) и перемещений первой перегородки (стеклопластик) от времени

Fig. 10. Diagram of the change in pressure in hydrogen (point 3) and the displacement of the first barrier (fiberglass) versus time

Заключение

Обнаружен сдвиг по фазе колебаний перегородки и возмущающего давления. Колебания перегородки отстают от колебаний давления на π/20.

Сдвиг по фазе означает наличие потерь и возможность их моделирования в упругой постановке.

Отставание колебаний перегородки от колебаний возмущающего давления означает возможность моделирования автоколебательных процессов в рассмотренной системе и поиск условий их возникновения.

Наблюдается зависимость поведения механической системы от вида рабочего тела.

Предложенная модель может быть использована для уточнения акустических расчетов.