Численное моделирование собственных колебаний частично заполненных жидкостью коаксиальных оболочек с учётом эффектов на свободной поверхности
Автор: Бочкарв С.А., Лекомцев С.В., Сенин А.Н.
Статья в выпуске: 1, 2022 года.
Бесплатный доступ
Работа посвящена численному анализу вертикально ориентированных упругих коаксиальных цилиндрических оболочек, внутренние полости которых полностью или частично заполнены неподвижной сжимаемой жидкостью. На её свободной поверхности принимаются во внимание эффекты плескания. Решение задачи осуществляется в осесимметричной постановке с использованием полуаналитического варианта метода конечных элементов. Поведение жидкой среды описывается волновым уравнением, которое совместно с условиями на границах приводится к слабой форме методом Бубнова - Галёркина. Математическая постановка задачи динамики тонкостенных тел формулируется с помощью вариационного принципа возможных перемещений и линейной теории тонких оболочек, основанной на гипотезах Кирхгофа - Лява. Давление жидкости на стенки конструкции вычисляется согласно уравнению Бернулли. Плескательные моды колебаний, обусловленные гравитационными эффектами на свободной поверхности жидкой среды, исключаются из разрешающей системы уравнений с помощью метода итерационной динамической конденсации. Верификация численной модели осуществлена путём сравнения с известными данными для случая одиночной оболочки, частично заполненной жидкостью. Проведена оценка влияния уровней заполнения полостей на низшие собственные частоты колебаний системы при различных вариантах кинематических граничных условий для оболочек (жёсткая заделка на обоих краях, консольное закрепление) и различной величине кольцевого зазора между ними. Установлено, что для рассмотренных конфигураций высота жидкости в кольцевом канале сильнее влияет на частотный спектр по сравнению с её уровнем в полости внутренней оболочки благодаря изменению частот колебаний в более широком диапазоне.
Метод конечных элементов, коаксиальные оболочки, потенциальная сжимаемая жидкость, свободная поверхность, плескание, линейная теория тонких оболочек, собственные частоты, динамическая конденсация
Короткий адрес: https://sciup.org/146282435
IDR: 146282435 | УДК: 539.3
Текст научной статьи Численное моделирование собственных колебаний частично заполненных жидкостью коаксиальных оболочек с учётом эффектов на свободной поверхности
ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2022PNRPU MECHANICS BULLETIN
Элементы машиностроительных конструкций в виде коаксиальных оболочек, кольцевой зазор между которыми и реже – внутренний объём заполнены текучей жидкостью, уже значительное время являются объектами разнообразных теоретических и экспериментальных исследований в связи с их широким распространением в различных областях техники [1]. Подробные библиографические обзоры, отражающие различные аспекты взаимодействия вложенных одна в другую соосных и имеющих эксцентриситет оболочек с неподвижной или текущей жидкостью, приведены в недавних статьях авторов [2–6]. Во введении данной работы будут процитированы только те немногочисленные публикации, в которых неподвижная жидкость располагается в обеих полостях, а упругая конструкция, как правило, имеет вертикальное расположение.
В статье [7] с использованием метода Бубнова – Галёркина получены простые расчётные формулы для определения частот колебаний коаксиальных оболочек с разными радиусами и разной высотой жидкости. В численном примере оценивается влияние жёсткости оболочек на спектр колебаний конструкции, полностью заполненной жидкостью. Совокупность вложенных одна в другую оболочек, полностью заполненных несжимаемой жидкостью, анализируется в [8]. Отсутствие жидкости во внутренней полости рассматривается как частный случай. При задании условия плескания на верхней границе столба жидкости делается предположение, приводящее практически к тем же результатам, что и при его отсутствии. Бесконечно длинные оболочки исследуются в статьях [9; 10]. В первой из них предложен простой и точный метод вычисления собственных частот колебаний полностью заполненных коаксиальных оболочек. В работе [10] также для случая полного заполнения обеих полостей установлено существование синфазных (направление и количество меридиональных полуволн совпадает для обеих оболочек) и противофазных (направления противоположны) форм колебаний. Численный анализ линейных колебаний оболочек, частично заполненных тяжёлой жидкостью, выполнен в работе [11] с применением метода конечных разностей. Приведены результаты для низших частот колебаний, полученных для разных отношений радиусов оболочек, полностью заполненных жидкостью. В публикациях [12; 13] приводятся постановка и решение задачи, учитывающие наличие жидкости в обеих полостях, но численные примеры сведены к частному случаю, когда жидкость полностью или частично заполняет только кольцевой канал. В аналитическом исследовании [14] рассматривается несоосное расположение оболочек, полностью заполненных жидкостью. Решение волнового уравнения, описывающего поведение жидкости в обеих полостях, осуществляется с помощью функций Бесселя. С этой целью в рассмотрение вводятся смещённые координаты, преобразование к которым выполняется посредством теоремы Бельтрами. Оценено влияние эксцентриситета на частоты колебаний при наличии подвижной среды в обеих полостях или только в кольцевом зазоре. Конечно-элементное решение, основанное на использовании изопараметрических эле- ментов, представлено в исследовании [15]. При фиксированной величине кольцевого зазора продемонстрировано влияние различия уровней жидкости внутри полостей на частоты колебаний слоистых оболочек при различных углах армирования. Влияние свойств вязкой несжимаемой жидкости, заполняющей коаксиальные оболочки, на амплитуды и скорости волн продольной деформации изучено в работе [16] с использованием физически нелинейных соотношений.
В перечисленных публикациях фактически отсутствуют работы, где в полной мере исследовано влияние как различного уровня жидкостей в обеих полостях, так и их размеров на частотный спектр конструкции. Наличие такого анализа будет способствовать более качественной оценке восприимчивости проектируемых объектов к внешним нагрузкам различной природы.
При частичном заполнении резервуаров воздействие гравитационного поля приводит к эффектам волнообразования (плескания) на свободных поверхностях жидкости [17]. В ряде вышеупомянутых работ [7; 8; 11; 15] соответствующее граничное условие учитывается в исходной постановке проблемы. Однако в данных публикациях не уточняется, что при этом решение модальной задачи осложняется появлением значительного количества плескательных собственных частот, величина которых или существенно уступает, или сопоставима с низшими связанными частотами колебаний конструкции. Данный факт значительно усложняет анализ полученных результатов [18]. Влияние гравитационных эффектов на динамические характеристики упругих конструкций, как свободно колеблющихся, так и подверженных внешним нагрузкам, более тщательно изучено для одиночных оболочек, частично заполненных жидкостью [19–36]. В некоторых работах предложены конструктивные решения (упругие или жёсткие мембраны) с целью предотвращения этого явления, представляющего опасность при определённых условиях эксплуатации. В работе [23] продемонстрировано, что при неблагоприятной комбинации геометрических и физико-механических параметров плескательные моды становятся сопоставимыми по величине со связанными модами гидроупругих колебаний и, следовательно, их учёт становится обязательным при моделировании. На основании вышесказанного целесообразным является разработка такого численного алгоритма, в котором учитывается плескание свободной поверхности, но соответствующие моды колебаний исключаются (редуцируются) из общего спектра частот с целью повышения вычислительной эффективности и удобства обработки получаемых результатов.
Использование техники понижения (редукции) исходной размерности разрешающей системы уравнений в рамках дискретных численных методов имеет длительную историю [37; 38]. За прошедшее время разработано значительное количество методов редуцирования, которые классифицируются по подходам, применяемым к построению координатной трансформации.
Помимо этих устоявшихся и широко используемых алгоритмов существуют различные варианты редукции. Некоторые из них учитывают, например, нестандартные методы решения (комбинация методов конечных и граничных элементов и т.п.) или специфические особенности поставленной краевой задачи и используются при изучении гидроупругих колебаний с учётом плескания жидкости [39–46].
Проведённые численные эксперименты показали, что наиболее простые и экономичные методы, связанные с редукцией физических координат (статическая конденсация Гайана, IRS-метод, метод динамической конденсации), не позволяют добиться или полного исключения плескательных мод, или приемлемой точности вычислений. Искомая цель достигается при использовании более затратного в вычислительном плане метода итерационной динамической конденсации [37] или терминологически корректнее – итерационной схемы решения для метода динамической конденсации. С его помощью в данной работе выполнено исследование фундаментальных частот колебаний коаксиальных оболочек, внутренние полости которых полностью или частично заполнены неподвижной сжимаемой жидкостью.
1. Математическая постановка задачи и основные соотношения
Рассматривается система (рис. 1), состоящая из вертикально ориентированных коаксиальных цилиндрических оболочек длиной L , радиусами R (1) , R (2) и толщинами h (1) , h (2) . Кольцевой зазор между оболочками и пространство внутренней частично заполнены идеальной сжимаемой жидкостью на высоты H (2) и H (1) соответственно. Здесь и далее верхний индекс «(1)» обозначает принадлежность к внутренней оболочке и заполняющей её полость жидкости, а «(2)» – к внешней оболочке и жидкости в кольцевом канале. Необходимо исследовать влияние уровней заполнения H ( i ) полостей соосных оболочек на низшие собственные частоты колебаний системы при различных значениях кольцевого зазора ( R (2) - R (1) ) и разных вариантах кинематических граничных условий для упругих тел.
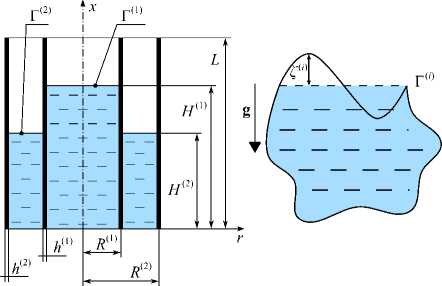
Рис. 1. Расчётная схема
Fig. 1. Computational scheme
Поведение идеальной сжимаемой среды описывается волновым уравнением относительной потенциала скорости φ ( i ) , которое в цилиндрических координатах ( x , θ , r ) принимает вид [47]
-
(i) ∂φ (i) 1 ∂ 2 φ (i)
Γ : =-
∂ ng ∂ t 2
∇ 2 φ ( i ) =
1 ∂ 2 φ ( i )
( c ( fi ) ) 2 ∂ t 2
С помощью метода Бубнова – Галёркина уравнение (1) с учётом граничных условий (2), (3) и (8) преобразуется к слабой форме [48]
где ∇ – оператор Лапласа, ∂ ( ⋅ ) ∂ ( ⋅ ) – частная производная, t – время, c ( f i ) – скорость звука в жидкой среде. Здесь и далее нижние и верхние индексы « f » и «( i )» ( i = 1,2 ) определяют жидкости, заполняющие полости оболочек, а индексы « s » и «( j )» ( j = 1,2 ) – упругие тела.
На смоченных поверхностях оболочек Σ ( ij ) задаётся условие непроницаемости
J V F - ^ф (1М V + J F»1
Vf (1)
J F" "
Σ (11) ∂ t
Vf (1)
1 ∂ 2 φ (1) ( c ( f 1) ) 2 ∂ t 2 d V
n d S + J V F n12 •Vф (2) d V +
Vf (2)
-
(2) 1 ∂ 2 φ (2) (2) ∂ u ˆ (1)
v kF - ( c(, ?)- d t - d V \V- d t S +
^ (ij ) = s ( i ) n s (j) . дф ( i ) = d u ( j )
fs ∂ n ∂ t
F n (1) 1 ∂ 2 φ 21) d S + F n (2) 1 ∂ 2 φ 22) d S
Γ (1) g ∂ t 2 Γ (2) g ∂ t 2
J F^ n d S = 0,
Σ (22) t
-
где S ( f i) и Ss (j) – поверхности, ограничивающие объёмы жидкости Vf (i) и оболочек Vs (j) ; u (j) , n – вектора перемещений оболочек и единичной нормали к их поверхностям.
На жёстком днище оболочек для потенциалов скоростей принимается граничное условие:
x = 0: ∂φ (i) = 0. (3)
∂ x
где φ ˆ ( i ) и u ˆ ( j ) – пробные решения для потенциалов скорости и векторов перемещений оболочек, Fn ( i ) и m ( f i ) – базисные функции и их количество.
Гидродинамическое давление, действующее со стороны жидкости на оболочки, вычисляется с использованием уравнения Бернулли
p ( ij ) = ( - 1) i + j - 1 ρ ( f i ) ∂φ ( i ) . (10)
∂ t
Волны на свободной поверхности жидкости Γ (i) описываются согласно допущению, что её фактическое положение находится на некоторой высоте ζ (i) относительно средней поверхности
Γ (i) (x = H (i) ): ∂ζ (i) =∂φ (i) ∂ t ∂ n.
Для получения уравнения плескания на свободной поверхности воспользуемся обобщённым уравнение Бернулли
p (i) +ρ (fi) ∂ ∂ φ t (i) +ρ (fi) g ζ (i) = 0, (5)
где p (i) – давление, g – ускорение свободного падения, ρ ( f i) – плотность жидкостей. Уравнение (5) с учётом условия на свободной поверхности
Γ (i) : p (i) = 0 (6)
принимает вид:
Γ (i) : ζ (i) =- 1 ∂φ (i) g ∂ t
Дифференцируя обе части равенства (1) по времени и подставляя результат в (4) окончательно получим
Компоненты вектора деформации определяются в цилиндрической системе координат ( x , θ , r ) с помощью классической линейной теории тонких оболочек, основанной на гипотезах Кирхгофа – Лява [49]
( j ) ( j ) ( j ) ( j ) ( j ) ( j ) ( j )T
ε = { ε xx , εθθ , γ x θ , χ xx , χθθ , χ x θ } =
[ du(j) 1 fdv(j) (a^ 1 du(j)
= i------,-l------+ wj) I,--+,
[ dx r ( d0 J r д0d d2w(j) 1 f dv^j^ d2w(j) | 2 f dv(j) d2wU) | dx2 r2 ^ dO dO2 Jr ^ dx dx d0 J где u(j), v(j)и w(j) – меридиональная, окружная и радиальная компоненты вектора перемещений, u = {u, v, w}T.
В матричном виде соотношения, устанавливающие связь между вектором усилий и моментов T ( j ) и вектором деформаций ε ( j ) , записываются как
T ( j ) = D ( j ) ε ( j )
Компоненты матрицы D ( j ) для изотропного материала известным образом определяется через модуль Юнга Es ( j ) и коэффициент Пуассона ν ( s j ) .
Математическая постановка задачи динамики тонкостенных упругих тел выполнена с использованием вариационного принципа возможных перемещений, который с учётом (2), (10) и работы сил инерции может быть представлен в следующем виде
J ( 5 e (1) ) T D (1) e (1) d S + J p S WV u (1) dV -
Ss (1) Vs (1)
J ( 5 u (1) ) T P (11) d S - J ( 5 u (1) ) T P (12) d S + ^ (11) ^ (12)
J ( 5 e (2) ) T D (1) e (2) d S + J p S 2’( 5 u (2) ) T U (2) dV -
Ss (2) Vs (1)
J ( 5 u (2) ) T P (22) d S = 0, a"1
где P ( j ’ = { 0,0, p (ij ’ } - векторы поверхностных нагрузок оболочек; p Sj ’ - плотность материалов оболочек.
2. Численная реализация
Здесь F ( i ) , N ( j ) и N ( j ) – функции формы для потенциала скорости жидкости, вектора перемещений оболочек и его нормальной составляющей; m f ’ , m 'j ’ , m £ j ) и m Г i ’ - количество конечных элементов, на которые разбиты объёмы жидкостей, оболочек, а также смоченные и свободные поверхности соответственно; B ( j ) – матрица градиентов, определяющая связь деформаций с узловыми перемещениями.
Решение системы (14) ищется в виде
{ ф (1) , u (1) , ф (2) , u (2) } = { ф (1) , u (1) , ф (2) , u (2) } exp( Z t ), (16)
где ф (1) , u (1) , ф (2) , u (2) - некоторые векторные функции координат, X = 5 + i to - характеристический показатель, 5 - величина, отвечающая за демпфирование системы, to - собственная частота колебаний, i - мнимая единица.
С учётом (16) система уравнений (14) преобразуется к виду
Численное решение задачи осуществляется с использованием полуаналитического варианта метода конечных элементов (МКЭ), при котором искомые переменные раскладываются в ряды Фурье по окружной координате 6 [50]. В результате чего исходная задача сводится к совокупности двумерных задач для каждой окружной гармоники j . Стандартные процедуры МКЭ позволяют получить из соотношений (9) и (10) следующую связанную систему уравнений, описывающую взаимодействие соосных оболочек с жидкостями в обеих полостях
( X 2 M + X C + K ) x = 0. (17)
Для нахождения X квадратичная проблема на собственные значения (17) сводится к обобщённой для несимметричных матриц удвоенной размерности
CK
- I
M
|
diag ! M.v + M |
(1) , M (1’ , M (,2’ + g , s , f |
M® , M ( 2’ } { ф (1) , u (1’ |
ф (2’ , u (2’ } T + |
|
" 0 |
- C (11’ |
0 0 " |
[ ф(” ' |
|
p f ’(C (11) ) T |
0 |
C (21) 0 |
l u (1’ L (14) |
|
0 |
-p f 2)( C (21’)T |
0 - C (22’ |
| ф (2’ |
|
0 |
0 |
p(2)( C (22’ ) T 0 |
[ u (2’ |
|
diag ’k.X K |
K K (2’ }{ ф |
1’ , u (1) , ф (2’ , u (2’ } T = 0 |
где типовые матрицы масс M , демпфирования C и жёсткости K для отдельных конечных элементов формируются следующим образом:
где I – единичная матрица.
При численной реализации для оболочек используется конечный элемент в виде усечённого конуса с аппроксимацией меридиональной и окружной компонент вектора перемещений линейным полиномом, а нормальной компоненты – кубическим. Дискретизация объёма жидкости проводится с помощью прямоугольного конечного элемента с линейной аппроксимацией потенциала скорости. В случае заполнения обеих полостей приемлемая точность вычислений достигается при размерности нередуцированной системы, равной 3198 степеням свободы. Численный алгоритм реализован в среде MATLAB с использованием возможностей пакета ANSYS для создания конечно-элементной сетки.
K (f ’ = Z J ( V F ( i ) ) T V F ( i ) d V , m ( f i ) Vf ( i )
M f ’ = ZJ; . ' ■ ( F (" ) T F ( i )d V • m f ’ V f i ’ ( c f )
3. Редуцирование системы уравнений
M g ) = Z J - ( V F ( i ) ) T V F ( i ) d S , m r i ’ S ( i 1 g
C ( j ) = Z J ( F ( i ) ) T N ( j ) d S , m l j ’ S £ ij ’
K Sj ) = Z J ( B ( , ) ) T D ( i ) B ( i ) d S , ms ( i ) Ss ( i )
M <j ) = Z J p j ( N ( j ) ) T N ( j ) d V . ms ( j ) Vs ( j )
Исключение плескательных мод колебаний, связанных с гравитационными эффектами на свободной поверхности жидкости, осуществляется методом итерационной динамической конденсации [37]. С этой целью перепишем уравнение (17), выделив главные (удерживаемые) x m и ведомые (редуцируемые) x s степени свободы, обозначив их нижними индексами «m» и «s» соответственно
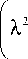
M mm
M sm
K mm
K sm
M ms
M ss
+ X
CC mm ms
С с
sm ss
K ms
K ss
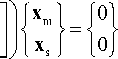
+
Степени свободы, относящиеся к перемещениям упругих тел и потенциалу скорости жидкости, за исключением расположенных на свободной поверхности, обозначим за главные. В качестве ведомых примем те, которые относятся только к свободной поверхности жидкости.
Представляя систему (19) в виде
LX r ) k ( k r ) k
IL -i о k Гх)k о
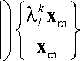
= 0.
5. Итерационная процедура завершается при выполнении условия
X2Mmm Xm +^Mms xs + XCmmXm + +XCms xs + Kmm xm + Kms xs = 0, kk
X l X l - 1
x k
X Xm xm + X2MssXs + XCsm xm + +XCss Xs + KsmXm + KssXs = 0, и выражая одни переменные через другие
X s =- (m +^ C ss + K ss )- 1 (^ M " x C + K sm ) X m = R m , (22)
получим редуцированную систему уравнений
X ' M + M ms R ) + X ( C + C ms R ) + I K + K ms R ) ) X m =
= ( X 2 M r + X C r + K r ) X m = 0.
Матрица преобразования R является частотно зависимой, поэтому для решения редуцированной системы (23) требуется использование описанной ниже итерационной процедуры.
Для каждого подлежащего определению k-го собственного значения Xk, вычисляемого с относительной погрешностью е, выполняются следующие шаги:
1. Задаётся начальное приближение Xk.
2. На каждой l-й итерации согласно (22) вычисляется матрица преобразования Rk (Xk-1)
3. В соответствии с (23) формируются матрицы редуцированной системы
4. Из редуцированной системы уравнений, приведённой к обобщённой проблеме на собственные значения для несимметричных матриц удвоенной размерности, определяется собственное значение Xk
4. Верификация модели / численного алгоритма
R k =- ( ( X k - 1 ) 2 M ss + X k - 1 C ss + K ss ) " *
( ( X k - 1 ) 2 M sm +X k - 1 C sm + K sm ) •
( M r ) k = M mm + M ms R k ,
( C r ) k = C mm + C ms R k , ( K r ) k = K mm + K ms R k •
где X k и X k - 1 - приближения, вычисленные на текущей и предыдущей итерациях. В противном случае последовательность действий повторяется, начиная с шага 2.
В связи с отсутствием подходящих для сравнения данных, полученных для коаксиальных оболочек, верификация численного алгоритма осуществляется на вертикальной цилиндрической оболочке, частично заполненной жидкостью ( L = 30 м, R = 25 м, h = 0,03 м, H = 21,6 м, E s = 2,06 Х 10 11 Па, v s = 0,3, р s = 7850 кг/м3, р f = 1000 кг/м3, C f = 1500 м/с) и свободно опёртой с двух торцов (SS, x = 0, L : v = w = 0). Аналитическое решение, полученное методом Рэлея – Ритца для указанной конфигурации, представлено в работе [24]. В таблице приведено сравнение собственных частот колебаний to , вычисленных для полной и редуцированной постановок, с результатами статьи [24]. Здесь через m обозначено количество полуволн в меридиональном направлении.
Данные таблицы демонстрируют хорошее соответствие результатов, определяемых в рамках описанного алгоритма, с известными сведениями. Применение метода итерационной динамической конденсации позволяет полностью исключить плескательные моды колебаний, а различие в связанных частотах, вычисляемых в полной и редуцированной постановках, не превышает 5 - 10 - 6 %.
5. Результаты
Представление полученных результатов расчётов осуществляется с помощью следующих безразмерных переменных: уровень заполнения жидкостью n ( i ) = H( i )/ L ;
Сравнение собственных частот колебаний ю (рад/с) свободно опёртой цилиндрической оболочки, частично заполненной жидкостью
Comparison of natural vibration frequencies to (rad/s) of a simply supported cylindrical shell partially filled with fluid
|
Моды |
Плескательные частоты |
Связанные частоты |
|||||
|
j |
m |
[24] |
Полная система |
Редуцированная система |
[24] |
Полная система |
Редуцированная система |
|
4 |
1 |
1.4425 |
1.4431 |
– |
13.658 |
14.061 |
14.061 |
|
2 |
1.9081 |
1.9111 |
– |
34.441 |
34.614 |
34.614 |
|
|
3 |
2.2305 |
2.2382 |
– |
49.692 |
49.532 |
49.532 |
|
|
4 |
2.5027 |
2.5176 |
– |
61.877 |
61.641 |
61.641 |
|
|
5 |
2.7444 |
2.7695 |
– |
71.804 |
71.793 |
71.793 |
|
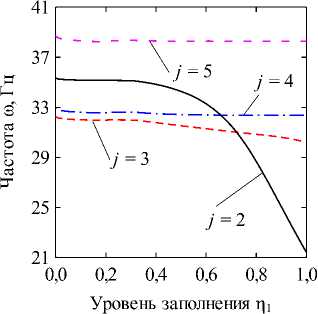
а
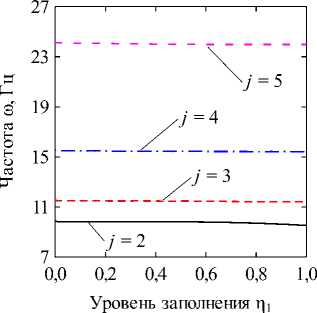
б
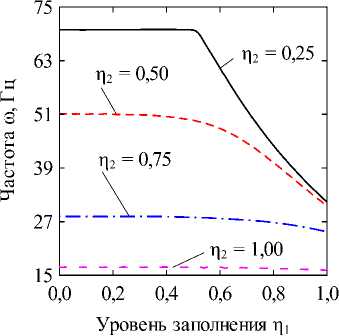
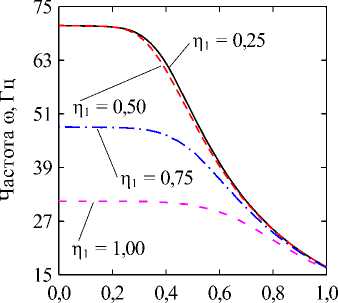
Рис. 2. Зависимости собственных частот колебаний to (Гц) от безразмерного уровня заполнения внутренней оболочки П 1 при различных уровнях заполнения кольцевого канала П 2 = 0,25 ( а ) и П 2 = 0,50 ( б ), полученные для различных значений окружной гармоники j : k = 1/100; CF
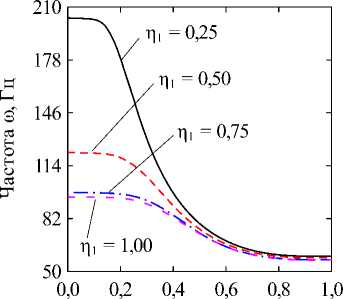
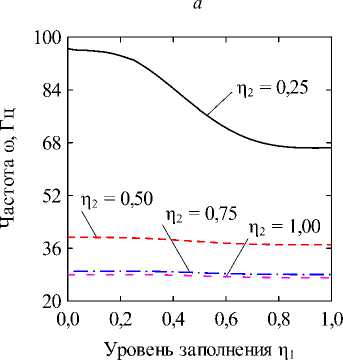
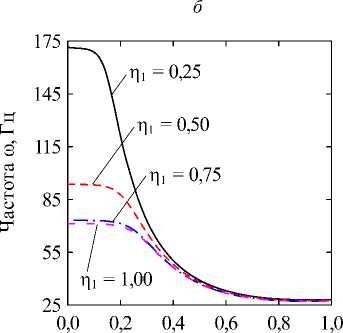
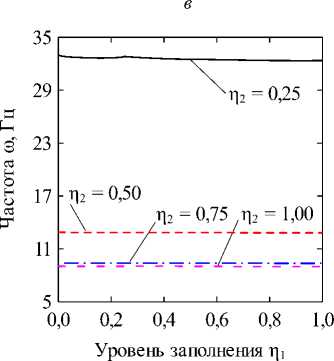
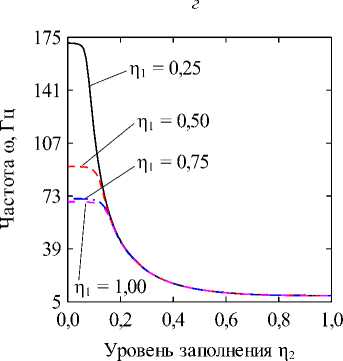
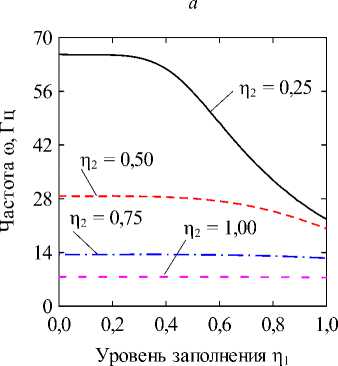
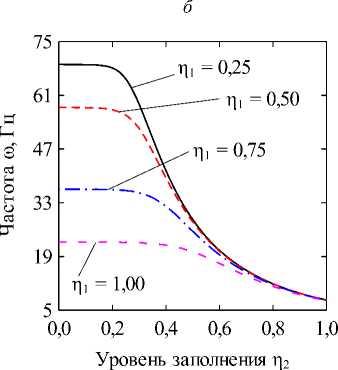
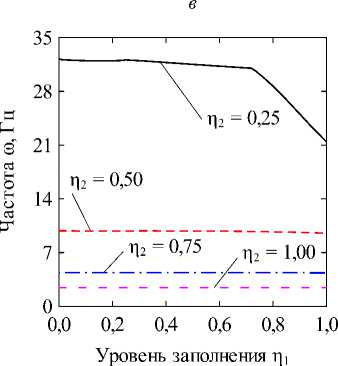
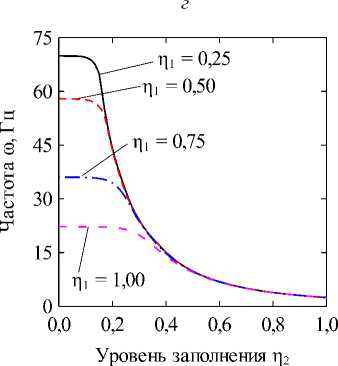
Fig. 2. The dependencies of natural frequencies to (Hz) on the dimensionless fluid level in the inner shell П1 at different levels of filling of the annular channel П2 = 0,25 (a) and П2 = 0,50 (б), obtained for different values of the circular harmonic j: k = 1/100; CF величина кольцевого канала k = (R(2) - R(1))/R(1). В численных примерах рассматривается система жёстко (CC, x = 0, L : u(j) = v(j) = w На рис. 2 отображены зависимости частот колебаний to (Гц) для нескольких окружных гармоник j от уровня заполнения внутренней оболочки П1 при различных уровнях заполнения кольцевого канала П2- На рисунках приводятся гармоники, соответствующие частоты колебаний которых близки к минимальному значению для каждой из рассмотренных конфигураций. Полученные графики позволяют наглядно оценить степень эволюции частот для каждого варианта заполнения. Для каких-то конфигураций различная чувствительность окружных гармоник к присоединенной массе жидкости в кольцевом канале обеспечивает смену форм с низшей частотой колебаний, тогда как для других этот фактор не имеет решающего значения. На рис. 3, 4 приведены зависимости низшей собственной частоты to (Гц) от уровня заполнения одного из каналов при фиксированной высоте жидкости в другом. Проанализированы оболочки с разными вариантами граничных условий при величине кольцевого зазора между оболочками, равной следующим значениям: k = 1/2; k = 1/10; k = 1/100. Из представленных результатов следует, что увеличение уровня заполнения в любой из полостей приводит к снижению значений минимальных частот колебаний системы вследствие возрастания присоединённой массы жидкости. Характерные изломы на графиках, в основном наблюдаемые при П2 = 0,25, информируют об изменении гармоники в окружном направлении j с минимальной частотой колебаний, как это продемонстрировано на рис. 2, а (кривые j = 2 и j = 3). Для рассмотренных конфигураций уровень заполнения кольцевого канала оказывает большее влияние на низшие частоты, поскольку в этом случае их значения изменяются в более широком диапазоне. При узком кольцевом зазоре колебательные характеристики системы могут определяться практически только уровнем жидкости в нём, как это имеет место для жёстко закреплённых оболочек (рис. 3, д). Представленные на рисунке зависимости позволяют сделать вывод, что уровень жидкости в полостях коаксиальных оболочек можно использовать для подбора частотного спектра конструкции, соответствующего требуемым условиям эксплуатации. Возможность управления значением низшей частоты колебаний посредством изменения уровня заполнения в одной из полостей снижается с повышением уровня жидкости в другой для всех рассмотренных комбинаций граничных условий и кольцевого зазора. Особенно сильно такое поведение проявляется при варьировании уровня заполнения полости внутренней оболочки при фиксированном уровне жидкости в кольцевом канале, когда последний достигает некоторого порогового значения. Представленные на рисунках данные демонстрируют также известную закономерность [1], проявляющуюся в снижении частот при повышении размеров внутренней оболочки. Заключение В работе представлены математическая постановка задачи и алгоритм её численной реализации, предназна- ченные для изучения колебательных характеристик сис- темы коаксиальных оболочек, внутренние полости Уровень заполнения р2 Уровень заполнения i]2 д е Рис. 3. Зависимости низших собственных частот колебаний ω (Гц) от безразмерных уровней заполнения внутренней оболочки η1 (а, в, д) и кольцевого зазора η2 (б, г, е), CC: (а, б) – k = 1/2; (в, г) – k = 1/10; (д, е) – k = 1/100 Fig. 3. Dependencies of the lowest natural vibration frequencies ω (Hz) on the dimensionless filling level of the inner shell η1 (а, в, д) and the annular gap η2 (б, г, е), CC: (а, б) – k = 1/2; (в, г) – k = 1/10; (д, е) – k = 1/100 которых полностью или частично заполнены идеальной сжимаемой жидкостью. На свободной поверхности жидкости принимаются во внимание эффекты плескания, обусловленные гравитационными силами. С целью повышения вычислительной эффективности плеска-тельные моды колебаний исключаются путём редуци- рования системы уравнений с помощью метода итерационной динамической конденсации. Использование такого подхода позволяет полностью исключить связанные с плесканием частоты и не вносит погрешность в спектр связанных частот. С использованием разработанного алгоритма проанализировано влияние уровней заполнения внутренних полостей соосных оболочек на фундаментальные частоты колебаний системы при разных размерах внутренней оболочки и граничных условиях. Установлено, что наибольшее изменение в спектре частот достигается путём варьирования высоты жидкости в кольцевом канале между оболочками. При этом ни комбинации кинематических граничных условий, задаваемых на краях конструкции, ни размеры кольцевого зазора, не оказывают качественного влияния на выявленные закономерности. Уровень заполнения г]2 д е Рис. 4. Зависимости низших собственных частот колебаний ω (Гц) от безразмерных уровней заполнения внутренней оболочки η1 (а, в, д) и кольцевого зазора η2 (б, г, е), CF: (а, б) – k = 1/2; (в, г) – k = 1/10; (д, е) – k = 1/100 Fig. 4. Dependencies of the lowest natural vibration frequencies ω (Hz) on the dimensionless filling level of the inner shell η1 (а, в, д) and the annular gap η2 (б, г, е), CF: (а, б) – k = 1/2; (в, г) – k = 1/10; (д, е) – k = 1/100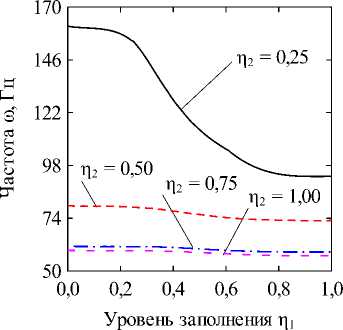
Список литературы Численное моделирование собственных колебаний частично заполненных жидкостью коаксиальных оболочек с учётом эффектов на свободной поверхности
- Païdoussis M.P. Fluid-Structure Interactions. Slender Structures and Axial Flow. – London: Academic Press, 2016. – Vol. 2. – 942 p. DOI: 10.1016/s1874-5652 (04) x8001-7
- Бочкарёв С.А., Лекомцев С.В., Сенин А.Н. Анализ пространственных колебаний коаксиальных цилиндрических оболочек, частично заполненных жидкостью // Вычислительная механика сплошных сред. – 2018. – Т. 11, № 4. – С. 448–462. DOI: 10.7242/1999-6691/2018.11.4.35
- Bochkarev S.A., Lekomtsev S.V., Senin A.N. Analysis of spatial vibrations of piezoceramic eccentric cylindrical shells interacting with an annular fluid layer // Frat. ed Integrità Strutt. – 2019. – Vol. 49. – P. 814–830. DOI: 10.3221/IGF-ESIS.49.15
- Бочкарев С.А., Лекомцев С.В. Гидроупругая устойчивость коаксиальных цилиндрических оболочек, выполненных из пьезо-электрического материала // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2019. – № 2. – С. 35–48. DOI: 10.15593/perm.mech/2019.2.04
- Hydroelastic stability of partially filled coaxial cylindrical shells / S.A. Bochkarev, S.V. Lekomtsev, V.P. Matveenko, A.N. Senin // Acta Mech. – 2019. – Vol. 230, No. 11. – P. 3845–3860. DOI: 10.1007/s00707-019-02453-4
- Бочкарёв С.А., Лекомцев С.В., Сенин А.Н. Анализ гидроупругой устойчивости несоосных цилиндрических оболочек, частично заполненных жидкостью // Вестник Самарского государственного технического университета. Серия: Физико-математические науки. – 2020. – Т. 24, № 1. – С. 95–115. DOI: 10.14498/vsgtu1746
- Балакирев Ю.Г. К исследованию осесимметричных колебаний соосных цилиндрических систем оболочек с жидким заполнителем // Инженерный журнал. МТТ. – 1968. – № 3. – С. 133–140.
- Пшеничнов Г.И. Собственные колебания коаксиальных ортотропных цилиндрических оболочек заполненных жидкостью // Труды 8-й Всесоюзной конференции «Теория оболочек и пластин», Ростов-На-Дону, 1971. – М.: Наука, 1973. –С. 546–549.
- Krajcinovic D. Vibrations of two coaxial cylindrical shells containing fluid // Nucl. Eng. Des. – 1974. – Vol. 30, № 2. – P. 242–248. DOI: 10.1016/0029-5493 (74) 90169-1
- Chen S.S., Rosenberg G.S. Dynamics of a coupled shell-fluid system // Nucl. Eng. Des. – 1975. – Vol. 32, № 3. – P. 302–310. DOI: 10.1016/0029-5493(75)90101-6
- Антонов В.Н. Колебания соосных цилиндрических оболочек, частично заполненных сжимаемой жидкостью // Известия АН СССР. МТТ. – 1977. – № 3. – С. 118–124.
- Швец Р.Н., Марчук Р.А. Осесимметричные колебания заполненных жидкостью соосных ортотропных цилиндрических оболочек // Прикладная механика. – 1985. – Т. 21, № 8. – С. 46–51.
- Fujita K. Vibration analysis of fluid-coupled two coaxial axisymmetric shells containing liquid // Bulletin of JSME. – 1986. – Vol. 29, № 248. – P. 516–524. DOI: 10.1299/jsme1958.29.516
- Jeong K.-H., Lee G.-M., Chang M.-H. Free vibration analysis of a cylindrical shell eccentrically coupled with a fluidfilled vessel // Comput. Struct. – 2001. – Vol. 79, № 16. – P. 1517–1524. DOI: 10.1016/S0045-7949(01)00031-1
- Okazaki K., Tani J., Sugano M. Free vibrations of a laminated composite coaxial circular cylindrical shell partially filled with liquid // Trans. Jpn. Soc. Mech. Eng. Part C. – 2002. – Vol. 68. – P. 1942–1949. DOI: 10.1299/kikaic.68.1942
- Mogilevich L., Ivanov S. Longitudinal waves in two coaxial elastic shells with hard cubic nonlinearity and filled with a viscous incompressible fluid // Recent Research in Control Engineering and Decision Making. ICIT 2020. Studies in Systems, Decision and Control / Dolinina O. et al. (eds). – Springer, Cham. – 2021. – Vol. 337. – P. 14–26. DOI: 10.1007/978-3-030-65283-8_2
- Ibrahim R.A. Liquid Sloshing Dynamics: Theory and Applications. – Cambridge: Cambridge University Press, 2005. – 970 p.
- Bochkarev S.A., Lekomtsev S.V., Senin A.N. Natural vibrations and stability of loaded cylindrical shells partially filled with fluid, taking into account gravitational effects // Thin Wall. Struct. – 2021. – Vol. 164. – 107867. DOI: 10.1016/j.tws.2021.107867
- Кулешов В.Б., Швейко Ю.Ю. Неосесимметричные колебания цилиндрических оболочек, частично заполненных жидкостью // Изв. АН СССР. МТТ. – 1971. – № 3. – С. 126–136.
- Free vibration analysis of cylindrical liquid storage tanks / T. Balendra, K.K. Ang, P. Paramasivam, S.L. Lee // Int. J. Mech. Sci. – 1982. – Vol. 24, № 1. – P. 47–59. DOI: 10.1016/0020-7403 (82)90020-0
- Chiba M., Yamaki N., Tani J. Free vibration of a clamped-free circular cylindrical shell partially filled liquid – Part I: Theoretical analysis // Thin Wall. Struct. – 1984. – Vol. 2. – P. 265–284. DOI: 10.1016/0263-8231(84)90022-3
- Chiba M., Yamaki N., Tani J. Free vibration of a clamped-free circular cylindrical shell partially filled with liquid – Part II: Numerical results // Thin Wall. Struct. – 1984. – Vol. 3. – P. 307–324. DOI: 10.1016/0263-8231 (84) 90002-8
- Lakis A.A., Neagu S. Free surface effects on the dynamics of cylindrical shells partially filled with liquid // J. Sound Vib. – 1997. – Vol. 207, № 2. – P. 175–205. DOI: 10.1006/jsvi.1997.1074
- Amabili M., Païdoussis M.P., Lakis A.A. Vibrations of partially filled cylindrical tanks with ring-stiffeners and flexible bottom // J. Sound Vib. – 1998. – Vol. 213, № 2. – P. 259–299. DOI: 10.1006/jsvi.1997.1481
- Jeong K.-H., Lee S.-C. Hydroelastic vibration of a liquidfilled circular cylindrical shell // Comput. Struct. – 1998. – Vol. 66, № 2–3. – P. 173–185. DOI: 10.1016/S0045-7949(97)00086-2
- Amabili M. Eigenvalue problems for vibrating structures coupled with quiescent fluids with free surface // J. Sound Vib. – 2000. – Vol. 231, № 1. – P. 79–97. DOI: 10.1006/jsvi.1999.2678
- Biswal K.C., Bhattacharyya S.K., Sinha P.K. Dynamic response analysis of a liquid-filled cylindrical tank with annular baffle // J. Sound Vib. – 2004. – Vol. 274, № 1–2. – P. 13–37. DOI: 10.1016/S0022-460X (03) 00568-6
- Kim Y.-W., Lee Y.-S., Ko S.-H. Coupled vibration of partially fluid-filled cylindrical shells with ring stiffeners // J. Sound Vib. – 2004. – Vol. 276, № 3–5. – P. 869–897. DOI: 10.1016/j.jsv.2003.08.008
- Lakis A.A., Bursuc G., Toorani M.H. Sloshing effect on the dynamic behavior of horizontal cylindrical shells // Nucl. Eng. Des. – 2009. – Vol. 239, № 7. – P. 1193–1206. DOI: 10.1016/j.nucengdes.2009.03.015
- Biswal K.C., Bhattacharyya S.K. Dynamic response of structure coupled with liquid sloshing in a laminated composite cylindrical tank with baffle // Finite Elem. Anal. Des. – 2010. – Vol. 46, № 11. – P. 966–981. DOI: 10.1016/j.finel.2010.07.001
- Оболочки вращения, частично заполненные жидкостью, при сейсмических и импульсных нагрузках / В.И. Гнитько [и др.] // Проблемы вычислительной механики и прочности конструкций. – 2012. – № 19. – С. 65–72.
- Бочкарёв С.А., Лекомцев С.В. Собственные колебания частично заполненных жидкостью некруговых цилиндрических оболочек с учётом плескания свободной поверхности // Вычислительная механика сплошных сред. – 2014. – Т. 7, № 4. – С. 471–480. DOI: 10.7242/1999-6691/2014.7.4.45
- Колебания жидкости в упругих оболочках с разным уровнем их заполнения / Д.В. Клименко [и др.] // Космическая техника. Ракетное вооружение. – 2015. – Вып. 3. – С. 24–29.
- Kashani B.K., Sani A.A. Free vibration analysis of horizontal cylindrical shells including sloshing effect utilizing polar finite elements // Eur. J. Mech. A/Solids. – 2016. – Vol. 58. – P. 187–201. DOI: 10.1016/j.euromechsol.2016.02.002
- Bochkarev S.A., Lekomtsev S.V, Matveenko V.P. Dynamic analysis of partially filled non-circular cylindrical shells withliquid sloshing // Int. J. Appl. Mech. – 2016. – Vol. 8, № 3. – 1650027. DOI: 10.1142/S1758825116500277
- Zarifian P., Ovesy H.R., Firouz-Abadi R.D. Sloshing effects on supersonic flutter characteristics of a circular cylindrical shell partially filled with liquid // Int. J. Numer. Methods Eng. – 2019. – Vol. 117, № 8. – P. 901–925. DOI: 10.1002/nme.5984
- Qu Z.-Q. Model order reduction techniques with applications in finite element analysis. – London: Springer, 2004. – 369 p.
- Игнатьев В.А., Ромашкин В.Н. Алгебраическая проблема собственных векторов и собственных значений высокого порядка в задачах динамики и устойчивости конструкций (обзор) [Электронный ресурс] // Интернет-вестник ВолгГАСУ. – 2015. – Вып. 2 (38). – URL: http://vestnik.vgasu.ru/?source=4&articleno=1946) (дата обращения: 10.10.2021).
- Felippa C.A., Ohayon R. Mixed variational formulation of finite element analysis of acoustoelastic/slosh fluid–structure interaction // J. Fluids Struct. – 1990. – Vol. 4. – P. 35–57. DOI: 10.1016/0889-9746(90)90036-5
- Andrianarison O., Ohayon R. Reduced models for modal analysis of fluid–structure systems taking into account compressibility and gravity effects // Comput. Methods Appl. Mech. Eng. – 2006. – Vol. 195, № 41–43. – P. 5656–5672. DOI: 10.1016/j.cma.2005.11.013
- Noorian M.A., Firouz-Abadi R.D., Haddadpour H. A reduced order model for liquid sloshing in tanks with flexible baffles using boundary element method // Int. J. Numer. Methods. Eng. – 2012. – Vol. 89. – P. 1652–1664. DOI: 10.1002/nme.3304
- Schotté J.-S., Ohayon R. Linearized formulation for fluid–structure interaction: Application to the linear dynamic response of a pressurized elastic structure containing a fluid with a free surface // J. Sound Vib. – 2013. – Vol. 332, № 10. – P. 2396–2414. DOI: 10.1016/j.jsv.2012.07.036
- Григорьев В.Г., Григорьева Е.В. Редукция поверхностных волн в конечно-элементном анализе колебаний упругих тел, содержащих жидкость // Проблемы машиностроения и надежности машин. – 2014. – № 6. – С. 11–16.
- Ohayon R., Soize C. Vibration of structures containing compressible liquids with surface tension and sloshing effects. Reduced-order model // Comput. Mech. – 2015. – Vol. 55, № 6. – P. 1071–1078. DOI: 10.1007/s00466-014-1091-4
- Ghalandari M., Bornassi S., Shamshirband S., Mosavi A., Chau K.W. Investigation of submerged structures’ flexibility on sloshing frequency using a boundary element method and finite element analysis // Eng. Appl. Comput. Fluid Mech. – 2019. – Vol. 13, № 1. – P. 519–528. DOI: 10.1080/19942060.2019.1619197
- Sotoudehni E., Shahabian F., Aftabi Sani A. A dynamic order reduction method for fluid-structure systems // Appl. Math. Model. – 2021. – Vol. 89, part 1. – P. 136–153. DOI: 10.1016/j.apm.2020.06.071
- Вольмир А.С. Оболочки в потоке жидкости и газа. Задачи гидроупругости. – М.: Наука, 1979. – 320 с.
- Бочкарев С.А., Матвеенко В.П. Численное исследование влияния граничных условий на динамику поведения цилиндрической оболочки с протекающей жидкостью // Известия РАН. МТТ. – 2008. – № 3. – С. 189–199.
- Бидерман В.Л. Механика тонкостенных конструкций. Статика. –М.: Машиностроение, 1977. – 488 с.
- Зенкевич О. Метод конечных элементов в технике. – М.: Мир, 1975. – 544 с.


