Численное моделирование сверхзвукового потока газов в коническом сопле с локальным подогревом плазмой и результаты экспериментов
Автор: Воронин С. Т.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Авиационная и ракетно-космическая техника
Статья в выпуске: 2 т.24, 2023 года.
Бесплатный доступ
Приводятся результаты основных теоретических расчётов и некоторых экспериментов по локальному подогреву низкотемпературной плазмой сверхзвукового потока газов внешним индуктором при ионизации газов в керамическом коническом сопле, осуществляемой посредством мощного высокочастотного электромагнитного поля. В основе численных расчётов лежат положения электромагнитной теории поля на основе уравнений Максвелла, Навье - Стокса для газодинамики, Саха - Эггерта для ионов и электронов, которые дают возможность рассчитать основные параметры индуктора и необходимую удельную мощность для подогрева низкотемпературной плазмой сверхзвуковых многокомпонентных газовых потоков. Использована модель безвихревого (ламинарного) сверхзвукового стационарного потока газов и проведено математическое моделирование его движения в коническом сопле с целью возможного использования эффекта дополнительного подогрева газового потока низкотемпературной плазмой для увеличения эффективности работы жидкостного ракетного двигателя. Установлено, что, для осуществления эффективного подогрева газового потока низкотемпературной плазмой в расчётном диаметре, требуется проводимость газов не менее σs ≥ 200 1/Ω·м для исходной температуры Та = 2528 - 2674 оК и частоты f = 27,12 МГц, что неосуществимо даже при наличии высокой концентрации примесей на основе щелочных металлов. Поэтому был разработан специальный прибор - ионизатор для камеры сгорания. Использование ионизатора позволяет достигнуть указанной проводимости для давления в камере сгорания 15 МПа. Расчёты показывают на возможность эффективного подогрева низкотемпературной плазмой сверхзвукового потока газов в начальном объёме конического сопла, который прилегает к критическому сечению жидкостного ракетного двигателя. Это позволит в дальнейшем значительно увеличить его удельный импульс и тягу на старте у поверхности Земли вследствие увеличения скорости потока газов в расчётном сечении. Также определено, что пристеночная область конического сопла обладает значительным градиентом температуры в радиальном направлении, тогда как вдоль оси симметрии конического сопла рост температуры имеет линейную зависимость. Результаты численного моделирования качественно согласуются с проведёнными экспериментами в кварцевом реакторе, охлаждаемом водой, что позволяло использовать разнообразные газовые и газо-жидкостные смеси для выбора топлива с оптимальным составом компонентов. Приводятся предварительные данные, полученные на рабочем стенде с тепловой мощностью кварцевого реактора, не превышавшей 4 кВт.
Низкотемпературная плазма, скин-слой, удельная высокочастотная мощность, давление магнитного поля, кварцевый реактор, окислитель нового типа
Короткий адрес: https://sciup.org/148326827
IDR: 148326827 | УДК: 533.9.03 | DOI: 10.31772/2712-8970-2023-24-2-309-324
Текст научной статьи Численное моделирование сверхзвукового потока газов в коническом сопле с локальным подогревом плазмой и результаты экспериментов
Подогрев газа низкотемпературной плазмой (НТП) в сверхзвуковом, коническом сопле, посредством внешнего электромагнитного высокочастотного (ВЧ) поля индуктора интересен для возможного локального подогрева потока газов, образующихся при сгорании топлива в камере сгорания (КС) жидкостного ракетного двигателя (ЖРД) с целью увеличения его тяги. Подогрев газов может происходить даже на относительно небольшом участке по сравнению со всей длиной сопла. Тем не менее в результате этого скорость атомов (ионов) может существенно увеличиться за счёт локального подогрева в поле индуктора при увеличении температуры движущегося потока газов при уменьшении его плотности, соответственно. В данной работе рассмотрены результаты численного моделирования процессов ионизации в коническом сопле для реальных, многоатомных газов, образующихся при сгорании топлива в КС для ЖРД. Данная задача усложняется многокомпонентностью газовой смеси, что увеличивает количество решаемых уравнений и требует расчёта значительного числа коэффициентов переноса и стандартных па- раметров. Нам неизвестны работы по моделированию подогрева плазмой сверхзвуковых потоков газовых смесей соответствующей плотности и с параметрами выхлопных газов от ЖРД, хотя сверхзвуковые потоки плазмы аргона и азота исследовались экспериментально [1]. Считается, что мощное, электромагнитное ВЧ-поле разогревает электроны до температуры значительно превышающей температуру окружающих нейтральных молекул, атомов, ионов, что соответствует двухтемпературной модели. В основу для расчётов положена изменённая теория для плазмотронов, работающих на смеси газов – азота, углекислого газа и воды. Удельная мощность электромагнитного ВЧ-поля принята соответствующей реальным возможностям генераторов ВЧ-энергии на мощных полупроводниковых приборах. В работе [2] рассматривалась задача такого дополнительного подогрева газового потока внешним источником, однако конечный отрицательный результат, в том числе для практического использования, выведен для прямой цилиндрической трубы, как у плазматронов, а не расширяющегося конического сопла. В этом случае локальный подогрев приводит к уменьшению плотности газов, но при движении по трубе газы втекают в пространство, занятое более плотным газом, и скорость их резко уменьшается. Это явление называется «тепловой кризис», и его основной причиной является снижение температуры (энтропии) вдоль цилиндрической трубы. В сверхзвуковом коническом сопле локальное повышение температуры уменьшает плотность газов в данной области, увеличивая их местную среднюю тепловую скорость Vа = (8kБТа/πmа)1/2, где kБ – постоянная Больцмана; Та – температура атомов (ионов); mа – масса атома (иона). Энтальпия hi в области подогрева и скорость газов Vа связаны с их давлением, но не по адиабате или политропически, а по более сложной нелинейной зависимости, характерной для плазмы, поэтому давление локальных «горячих» газов будет всегда превышать давление в области не подвергнувшейся подогреву, а локальная плотность газов значительно снизится. Это следует из первого закона термодинамики: тепло dQ, подводимое газу извне, например, посредством его локального индукционного нагрева, может расходоваться только на повышение внутренней энергии газов dU и работу по его расширению (деформации) pdV, причём dU = ˂ cp ˃ ∙dT, где ˂ ср ˃ – средняя теплоёмкость локального объёма газов; dT – изменение температуры вследствие дополнительного подогрева; р – давление газов в локальном объёме; dV – изменение объёма, обратно пропорциональное изменению плотности газов ρ. В наших расчётах также учитывалось изменение ˂ ср ˃ от локальной температуры и определялось изменение dT и dV~1/dρ, что однозначно приводило к увеличению температуры, объёма и скорости потока газов.
Теоретически может возникнуть ситуация, когда давление газов, расширяющихся из-за локального подогрева, сравнится или превысит статическое давление, обусловленное расширением сопла, которое будет недостаточным по сравнению с энергией локального подогрева газов. Такое может произойти при малых степенях расширения длинного конического сопла или при достаточно высоких удельных мощностях подогрева (температурах), но так как потери на излучение увеличиваются пропорционально четвёртой степени температуры, то эффективность подогрева газового потока плазмой тогда резко снижается. Следовательно, выбор степени расширения сверхзвукового конического сопла и величины энтальпии h i внешнего подогрева плазмой потока газов взаимосвязаны и должны иметь некоторую оптимальную величину. Для оценки возможного увеличения скорости потока газов в ЖРД проводилось численное моделирование процессов, происходящих в сверхзвуковом коническом сопле на основе газодинамических функций из работы [3]. В зоне плазменного подогрева, ограниченного объёмом строго под витками индуктора, для упрощённой модели при расчётах использовался метод контрольного объёма с локальной аппроксимацией газодинамических функций, подробно описанного в работах [4; 5], где также приведены программы расчётов плазмы для редактора MathCAD2001 Professional.
1. Постановка задачи
Образование и движение плазменного потока в сверхзвуковом коническом сопле сопровождается рядом существенных отличий от расширения газов без внешнего подогрева: a) происходит частичная диссоциация молекул из-за роста температуры газа Та вдоль оси индуктора, иначе изменение их молекулярного веса; б) давление в плазме перестаёт изменяться по известным термодинамическим функциям при уменьшении плотности газов вследствие зависимости удельных теплоёмкостей ср, теплопроводности χa и вязкости µa плазмы от температуры ионов и атомов Та; в) внутри зоны разогрева газов плазмой образуются круговые электронные токи, текущие поперёк продольных газовых потоков, полностью заполняя объём под витками индуктора, а проводимость газов σs значительно изменяется по длине подогреваемого объёма; г) появившийся электронный газ лоренцевского типа, в котором электроны передают свою кинетическую энергию молекулам, атомам и ионам в процессе множества столкновений; д) в образующейся плазме газового потока температура электронов Те ˃˃ Та, и можно считать, что ионы и атомы малоподвижны по сравнению с электронами; е) скорости ионов и атомов подчиняются статистике Максвелла – Больцмана, а образование ионов и электронов можно описать системой известных уравнений Саха – Эггерта; ж) плазма в подогреваемом объёме в целом квазинейт-ральна, а степень ионизации ion˂˂1; з) дрейфовая скорость ионов и электронов в электрическом поле индуктора меньше их тепловой скорости.
2. Исходные данные и начальные условия
Сверхзвуковые потоки газов считаются ламинарными и безвихревыми, т. е. rot(W) = 0, где W – локальная скорость газового потока. Перенос тепла излучением для НТП не учитывается вследствие низких расчётных температур для электронов Те ˂ 3750 оК, а для молекул, атомов, ионов Та ˂ 3200 оК. Область, занятая плазмой, отделена от витков индукторов охлаждаемым коническим керамическим соплом с температурой поверхности То = 1000 оК. Рабочая частота f = 27,12 МГц соответствует тому, чтобы воздействие электромагнитного ВЧ поля, определяемое величиной скин-слоя ∆p в нашей конструкции конического сопла, происходило наиболее эффективно. Параметры образующейся плазмы на входе индуктора сильно зависят от проводимости втекающего газа, который обычно имеет небольшую проводимость σo ˂ 20 1/Ω·м для типичных температур газов в начале сопла Tа = 2528 – 2674 оK, что соответствует давлениям в камере сгорания ЖРД ~1 – 15 МПа. Этой величины σ0 недостаточно для оптимального поглощения электромагнитного ВЧ поля и эффективного подогрева потока газов в индукторе даже при наличии щелочных металлов. Если же некоторым способом повысить степень ионизации газов, то величина их проводимости достигнет оптимальной величины σs ~ 200 1/Ω·м на входе в сопло. В этом случае подогреваемый и достаточно проводящий газ будет нагрузкой и частью магнитной системы индуктора. Тогда «горячие» электроны образуют короткозамкнутый виток виртуального трансформатора с большой плотностью тока, направленного навстречу первичному току обмотки индуктора. Если электромагнитная ВЧ энергия проникает на глубину скин-слоя ∆p, соизмеримого с входным радиусом Rin индуктора, то на этой глубине поглощается около 87 % энергии, подогревающей сверхзвуковой газовый поток. В противном случае эффективность передачи ВЧ энергии будет незначительной. Геометрические размеры для конического сопла и индукторов подбирались на основе предварительного моделирования с целью наиболее эффективного подогрева газов индуктором и согласования индуктора с генератором ВЧ-энер-гии. На основе известных из литературы зависимостей теплоёмкости плазмы газов cp от температуры [4–7] был произведён численный расчёт полной энтальпии Σhi для интервала температур ΔТ = 2500 – 3750 ºК с учётом доли энергии 10–18 %, затраченной на частичную диссоциацию Н2О и СО2 по работе [8] для давлений ~ 0,1 – 0,25 МПа. Молекулы азота N2 считались не диссоциироваными. В результате были получены следующие значения: для водорода – hi(H2) = 158,1 МДж/кг; кислорода – hi(O2) = 8,1 МДж/кг; углекислого газа – hi(CO2) = 6,9 МДж/кг и азота – hi(N2) = 2,8 МДж/кг. Состав газов при входе в зону нагрева плазмой был выбран для стехиометрического соотношения керосина к азотной кислоте равного 5,5 [3]. Тогда молекулярная доля газов составляет N2 ~ 18,5 %, H2O ~ 32 %, CO2 ~ 43 %, прочие окислы ~ 6,5 %. С учётом доли ki каждого вида молекул, суммарная энтальпия плазмы на участке подогрева, равна Σhi= hi(H2) ∙ 0,0364 + hi(CO2) ∙ 0,4373 + hi(O2) ∙ 0,2916 + hi(N2) ∙ 0,1854 = 11,7 МДж/кг для интервала ΔТ = 2500 – 3750 ºК. Все расчёты проводились для одной конкретной геометрии конического сопла с внутренним входным диаметром Dcr = 10 мм для критического сечения, выход- ным диаметром Dout = 60 мм и длиной сопла Lс = 150 мм. Толщина диэлектрических охлаждаемых стенок сопла 8 мм. Тепловая мощность КС составляла 26 кВт при её объёме 0,5 ∙ 10–3 м–3 (радиус 3,8 см и длина ~11 см). Удельная тепловая мощность для КС равнялась 52 Вт/см3 для расчётной топливной пары керосин – азотная кислота при рабочем давлении в камере сгорания 1 МПа и скорости потока газов в критическом сечении Wcr = 997 м/с для расхода топлива G = 0,052 кг/с [3]. Расчётная удельная ВЧ-мощность электромагнитного поля составляла ~1200 Вт/см3 и значительно превышала удельную тепловую мощность для КС. Энергия электронов kБTe ∙ 3/2, передаваемая посредством столкновений атомам (ионам), принята постоянной во всём объёме и соответствует их температуре Те = 3750 оК за исключением небольшой области у поверхности сопла, где температура электронов близка к температуре атомов (ионов).
3. Расчёт локального подогрева потока газов плазмой
В литературе довольно много работ по моделированию плазменных потоков в сложных газовых смесях, однако большинство из них исследует дозвуковые плазменные потоки с высокой энтальпией при малых расходах газа [6; 9]. Поэтому представляет особый интерес моделирование и исследование процесса подогрева плазмой сверхзвуковых газовых потоков достаточно высокой плотности. Уравнение для энергии атомов, ионов и электронов для каждой доли k i локального объёма можно представить в следующем виде:
( n a + n i ) ∙ k Б ∙ Т а ∙ 5/2 + n e ∙ k Б ∙ Т е ∙ 3/2 = k i ∙ Σ h i ∙ ρ i , (1)
где n a , n i , n e , м–3 – локальные концентрации атомов, ионов и электронов; ρ i , кг/м–3 – локальная плотность газов. Для описания скорости потоков расширяющихся газов, можно использовать дифференциальные уравнения Навье – Стокса для потоков газа с учётом сил внутреннего трения и сил Лоренца в магнитном поле индуктора по работе [2]:
—
-
( Р ) = р- J - grad ( P ) + V 2 ( ^ • W ) + - grad ( ^ • divW ) — = - div ( р- W — ) , (2)
dt 3 ∂t где W – вектор потока газа; J – вектор силы Лоренца для ионов в магнитном поле индуктора; Р – давление газа. Для упрощения системы дифференциальных уравнений (2), можно оценить его составляющие и рассмотреть стационарный случай. Максимальное значение силы Лоренца для иона в магнитном поле индуктора будет равно FL = q ∙ Wr ∙ µv ∙ I ∙ Ni / (2 ∙ Rc) ≈ 3,4 ∙ 10–18 Н, где q – заряд электрона; Wr ~ 2000 м/с – радиальная составляющая скорости потока; I = 71 А, средний ток индуктора; Ni = 4 – количество витков индуктора; Rc = 6,7 мм – средний радиус конического сопла; µv – магнитная постоянная вакуума. Сила статического давления газов вдоль продольной оси, приведённая к одному атому (иону), равна Fz = Pс ∙ π ∙(Rc)2/nс ~ 1,8 ∙ 10–14 Н, где Pс ~ 0,2 МПа – среднее давление в сопле; nс ~ 2 ∙ 1015 м-3 – количество атомов (ионов) в среднем сечении сопла. Поэтому отношение Fz / Fл ˃ 103 и силой Лоренца для ионов по сравнению с силой статического давления для атомов можно пренебречь, а это и означает, что rot(W) = 0, как мы и предположили во втором разделе. Тогда уравнения (2) для вектора скорости потока газов вдоль сопла приводятся к следующему расчётному уравнению:
∂ 2 W 3 ∂ P =⋅
∂ z 2 4 ⋅ µ a ∂ z .
Также необходимо использовать исходное уравнение баланса энергии для газов, имеющее следующий вид в дифференциальной форме по работе [4]:
d T —
ρ⋅сp( a +W ⋅grad(Ta))=σs⋅Eθ2 + div(χa ⋅ grad(Ta)), ∂t где Еθ – электрическое поле внутри индуктора. В уравнении (4) источником внутреннего тепла является Джоулев нагрев, а потоки тепла появляются из-за теплопроводности электронов, ионов, атомов и молекул. С учётом сделанных выше упрощений, можно преобразовать уравнение (4) в расчётное безразмерное уравнение для стационарного случая
∇ 2Ť а - А 1 ∇ Ť а = - А 2 , (5)
где А 1 = G ∙ с p / ( S i ∙ χ а ); S i – расчётное сечение сопла i = 1..10; А 2 = σ s ∙ ( Е θ )2 / χ а ; Ť a = T а / Т о – безразмерная температура. В этой работе использовались табличные данные коэффициентов вязкости и теплопроводности, линейно зависящих от температуры, взятые из работы [8], так как расчётная температура ионов и атомов фактически не превышала Т а ˂ 3087 оК. Расчёт проводимости плазмы σ s (T) проводился на основе известной системы уравнений Саха – Эггерта для каждой компоненты НТП, которые определяют их вклад в общую проводимость по закону Дальтона. Данные уравнения для расчёта концентраций ионов и электронов для доли каждого вида атомов k i имеют следующий вид:
n ( T ) = Σ n i ( T ), n i ( T ) = k i ∙( g + / g a )1/2·(A· N cs )1/2·( T )3/4·exp[- q (Δε i - Δ I ) / 2 k Б Т ], (6)
где A = 2(2π · m e · k Б / h 2 )3/2; g a , g + – безразмерные нормировочные множители для одноатомных, двухатомных и многоатомных молекул газов и их ионов; N cs , м–3 – концентрация атомов и молекул на входе в расчётное сопло; Δε i , э-В – энергия ионизации атомов; Δ I , э-В – энергия экранирования ионов электронами, зависящая от их концентрации и температуры по формуле Эккера – Вейцеля [7]; h – постоянная Планка; m e – масса электрона; k i – доля атомов (ионов): азота, кислорода, водорода, углерода. Всего рассчитывалось 14 компонент атомов и ионов с учётом данных по диссоциации газов из работы [8]. Проводимость плазмы, определяемая температурной ионизацией атомов и молекул, σ о = (π · ε · q 2· n ( T )/8 m e )1/2, где ε – диэлектрическая постоянная вакуума. Глубина среднего проникновения Δ р электромагнитного ВЧ-поля (скин-слой) определяется известным соотношением Δ p = [2/(μ v · σ s ( T ) · 2π f )]1/2. Суммарная проводимость плазмы σs( T ), определяемая концентрацией атомов и молекул по формуле (6), а также дрейфом электронов в сильном электромагнитном ВЧ-поле, выражается следующими формулами:
σs(T) = q ∙ n(T) ∙ [μo(T) + μdr(T)],(7)
μo(T) = (q/me) · (RД/Vet(T)) = [π · ε/men(T)]1/2,(8а)
μdr(T) = (q/me) · (Lea/Vet(T)) = [(q/me) · (1/Vet(T))] · (1/QeaNa),(8б)
где R Д = [ε · k Б T / q 2 n ( T )]1/2 – длина Дебая; V et = (8 k Б Т e/π m е)1/2 – средняя тепловая скорость электронов; μ о ( Т ), м2/В∙с – подвижность электронов при отсутствии электрического поля; μ dr ( T ), м2/В ∙ с – подвижность электронов в электрическом поле; L ea , м – средняя длина свободного пробега электронов в электрическом поле до взаимодействия с атомами; N a , м–3 – средняя концентрация атомов в каждом расчётном объёме; Q ea ≈ 16 ∙ 10–20, м2 – среднее сечение взаимодействия электронов с атомами кислорода, азота и углерода по Рамзауэру [6]. Различие в величине подвижностей μ o ( T ) и μ dr ( T ) объясняется различным временем взаимодействия электронов с атомами: для малой длины Дебая R д при тепловом движении вблизи атомов и большой дрейфовой длиной пробега L ea при движении между атомами и молекулами в электрическом ВЧ-поле. Такой подход к вычислению подвижностей электронов и проводимости σ s ( T ) позволяет улучшить сходимость вычислений, особенно в граничных областях на входе и выходе из зоны плазменного подогрева конуса. Расчёт степени ионизации ion ( T ) для диапазона температур Т а = 2586 – 3750 оК для давлений 0,1–0,2 МПа даёт величину, лежащую в интервале 3,2 ∙ 10–4 –7 ∙ 10–3. На рис. 1 приведён расчёт суммарной проводимости газов σ s (T) для локального давления 0,25 МПа.
Иной подход для расчётов предложен в работе [9], в которой рассматривались поток электронного газа и поток колебательной энергии атомов с учётом бародиффузии в двухтемпера- турной модели (электронов и ионов) с вычислением коэффициентов вязкости и теплопроводности по приближённым формулам Уилке – Васильевой [10], причём проводимость плазмы определялась из соотношения Стефана – Максвелла. Данный подход объясняется тем, что градиент радиальных потоков достигал ΔTa ~ 5000 оК. Скорости для имевшихся вихревых потоков обладали высокими градиентами при небольших расходах газов G ~ 2,4–4,8 г/с. Температура плазмы достигала 2 · 104 оК, для неоднородного, вихревого потока газов по вышеуказанной работе, когда основные потери энергии – это излучение света, характерное для ВЧ плазматронов.
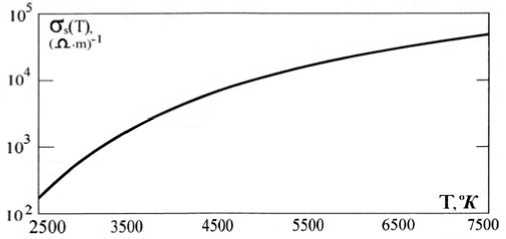
Рис. 1. Зависимость суммарной локальной проводимости газов σs(T) от их температуры при давлении 0,25 МПа
Fig. 1. Dependence of the total local conductivity of gases σs( T ) on their temperature at a pressure of 0.25 MPa
4. Определение составляющих высокочастотного поля
Распределение электрического и магнитного полей в коническом сопле требует обязательного расчёта напряжённости электромагнитного ВЧ поля Ė θ в комплексной форме по уравнениям Максвелла. Их можно свести к одному уравнению для тангенциальной компоненты комплексного Ė θ при магнитной проницаемости плазмы равной 1, если рассматривать поля в рамках осевой симметрии и пренебречь токами смещения, согласно работе [6]:
•
∂ 2 E ∂ 1 ∂• •
θ + [( rE θ ) =- j ωµ v σ sE θ ,
∂z2 ∂rr∂r где j – мнимая единица; ω – угловая частота. Также нужно использовать уравнения для связи векторного потенциала магнитного поля Ḣm и напряжённости электрического поля Ėθ в комплексной форме по работе [11] для индукционного нагрева:
•
∂ • E θ •
( E θ ) + =- j ωµ v H m
∂ rr
•
∂ Hm =- σ s E • θ 1 ⋅ ∂ ( rE • θ ) = j ωµ v H • m →〈 r = R c 〉 . (10) ∂ r r ∂ r
Начальные условия для уравнений (9), (10) были аналогичны работе [12]: при r = 0, Е θ = 0; при r = R с , Н mе (z) = const – есть амплитуда магнитного поля на внутренней поверхности диэлектрического конуса вдоль конического сопла, ограниченного витками индуктора. Решение уравнений (9) и (10) получено в работе [11] в цилиндрических функциях Бесселя для относительной безразмерной координаты m = ( R /∆ p ) ∙ √2, где R , – переменный радиус конического сопла, м. Соответствующие решения для модулей H m, и Е θ, а также для комплексной амплитуды плотности тока электронов и его модуля δ m получены для функций Бесселя ber( m ) и bei( m ) в следующем виде [11]:
⋅ ber ( m ) + j ⋅ bei ( m ) H = H ber 2( m ) + bei 2( m )
ber(m2)+j⋅bei(m2), mmeber2(m2)+ bei2(m2), где Hme = Wo ∙ Ii ∙ √2 / Li, (А ∙ виток)∕м; Wo – число витков; Ii, А – ток индуктора; Lи, м – длина ин- дуктора; m2= (Rin / ∆p)√2; Rin, м – входной радиус расчётного объёма сопла,
5 m = 5 me
ber ' ( m ) + j • bei ' ( m ) ber ( m 2 ) + j • bei ' (m 2 ) ,
5 = 5
mme
[ ber ' ( m )] 2 + [ bei ' ( m )] 2 ber 2 ( m 2 ) + bei 2 ( m 2 ) ,
где δ me = H me · √2/∆ p , А/м2 – плотность тока электронов у сопла; функции berʹ( m ) и beiʹ( m ) – это производные по “ R ” от соответствующих функций. На рис. 2 приведены результаты расчёта по формуле (11) для безразмерных функций Ψ Нme1 ( m ) = H m / H me1 , Ψ Нme2 ( m ) = H m / H me2 , описывающих изменение магнитного поля и равных отношению амплитуд от безразмерной координаты m для параметров m 2 = 1,6202 и 0,8101. Связь величины модуля для электрического поля E m и модуля плотности тока δm определяется по закону Ома: δm = σs ∙ E m и равна нулю при m = 0 ( R = 0) для соответствующего значения по оси конусного сопла. Электрическое поле E m ( m ) изменяется от координаты m по зависимости близкой к линейной для параметров m 2 ˂ 3,2 и значений m < 4.
Плотность тока на оси сопла равна нулю вследствие равенства нулю электрического поля и максимальна у поверхности конического сопла, что указывает на поток тепловой энергии ВЧ-поля, идущий от поверхности к оси конического сопла.
Результаты расчёта по формуле (12) для безразмерных функций Ψ δme1 ( m ) = δ m / δ me1 , Ψ δme2 ( m ) = = δ m / δ me2 приведены на рис. 3 и описывают распределение плотности тока для параметров m 2 = 1,6202 и 0,8101, соответственно.
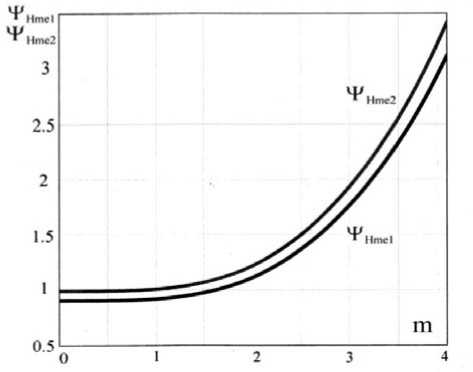
Рис. 2. Зависимости безразмерных функций ΨНme1 иΨНme2 от безразмерной координаты m
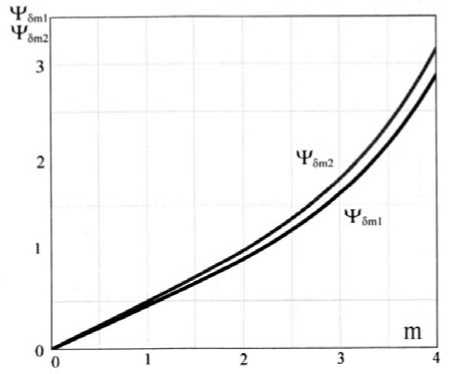
Рис. 3. Зависимость безразмерных функций
Ψ δme1 = δ m / δ me1
, Ψδme2 = δm/ δme2
-
Fig. 2. Dependencies of dimensionless functions ΨHme1 and ΨHme2 on the dimensionless coordinate m
от безразмерной координаты m
-
Fig. 3. Dependence of dimensionless functions
Ψ δme1 = δ m / δ me1, Ψ δme2 = δ m /
δme2
on the dimensionless coordinate m
Ранее отмечалось, что при оптимальной удельной проводимости σ s , величина скин-слоя ∆ p должна примерно соответствовать входному радиусу в расчётном конусе R in . Тогда основная часть электромагнитной ВЧ-энергии будет поглощаться наиболее эффективно по всему сечению для конусного объёма, а весь поток будет прогрет до заданной температуры. В этом случае, оптимальное расчётное значение m 2 находится в интервале от 1,6 до 3,2 и связано с частотой электромагнитного ВЧ-поля и величиной изменяющейся средней проводимости плазмы σ si в каждом расчётном объёме.
Электромагнитная ВЧ-волна движется по нормали от поверхности индуктора. Энергия волны Ṡp пропорциональна векторному произведению комплексно сопряжённых электрического Ėm и магнитного Ḣm полей. Известно, что магнитное поле, определяющее реактивную энергию индуктора, переходит в активную энергию электрического поля с частотой колебаний электро- магнитной ВЧ-волны, при этом происходит осцилляция плотности электронов, изменение их дрейфовой скорости и рост температуры носителей заряда, соответственно. Опуская выкладки, приведём окончательное выражение для Ṡp:
Ṡ p = – {( H me )2 m 2 / (2√2∙ σ s ∙∆ p )}[Ψа + j∙Ψр],
где Ψа, Ψр есть функции от m 2 , которые определяют активную и реактивную мощность, соответственно. Здесь
T a = — • m2
ber ' ( m 2 ) • ber ( m 2 ) + bei ' ( m 2 ) • bei ( m 2 ) ber 2 ( m 2 ) + bei 2 ( m 2 )
2 bei ' ( m 2 ) • ber ( m 2 ) - ber ' ( m 2 ) • bei ( m 2 ) ---::---------------------------------т-------------------------------------------- m 2 ber 2 ( m 2) + bei 2 ( m 2)
На рис. 4 приведены графики безразмерных, вспомогательных функций для активной Ψа и реактивной Ψр компоненты электромагнитного ВЧ-поля, рассчитанных по формуле (14), которые полностью определяют параметры электромагнитной волны ВЧ-поля с вектором Ṡ p , а также соотношения η( m ) = Ψа/Ψр, пропорционального локальной эффективности подогрева газов плазмой. Видно, что расчётная эффективность в оптимальном диапазоне m менее ˂ 70 %. Вектор Ṡ p можно представить состоящим из двух ортогональных составляющих – аксиального и радиального векторов. Аксиальный вектор совпадает с потоком газов и является дополнительным источником, ускоряющим поток газов, хотя и незначительным, и равным произведению модуля Ṡ p ·sin(9032ʹ) в нашем случае.
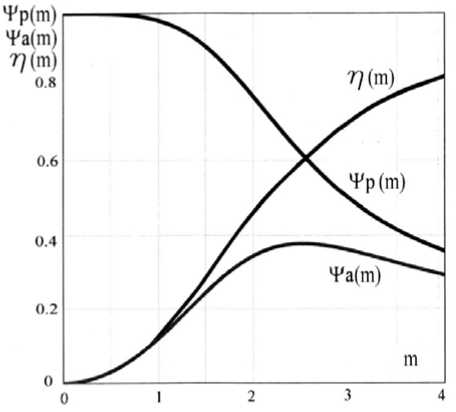
Рис. 4. Графики безразмерных функций для активной Ψа и реактивной Ψр компоненты электромагнитного ВЧ поля, а также их соотношения η( m ) = Ψа / Ψр от безразмерной координаты m
Fig. 4. Graphs of dimensionless functions for the active Ψa and reactive Ψp components of the electromagnetic RF field, as well as their ratios η( m ) = Ψa / Ψp from the dimensionless coordinate m
Радиальный вектор отклоняет поток ионов от стенок к центру. Он равен произведению модуля Ṡп·cos(9032ʹ), соответственно. Расчёт для модуля Ṡp даёт незначительное продольное давление Pм ≈ 30 Па для тока индуктора Ii = 71 А. Давление Pм увеличивается с ростом произведения тока на число витков в квадратичной зависимости и может достигать значительной величины. Этот эффект увеличения тяги ЖРД можно использовать в глубоком вакууме при значительном токе индуктора и воздействии аксиальной компоненты электромагнитного ВЧ-поля на поток газов. Для керамического конуса прилегающая к плазме поверхность будет заряжена положительно в соответствии с законом Пуассона по формуле Ψe = (kБ · Те / 2q)ln(Mi / 2πme), где Ψe, В – потенциал; Mi, кг – средняя масса иона. Расчёт даёт величину Ψe ≈ 2 В для Te ≈ 3750 оК и средней массе ионов Mi ~ 5 ∙ 10-26 кг. Следовательно, небольшой объёмный заряд около поверхности конуса будет влиять на распределение зарядов у поверхности конусного сопла, что может служить некоторым “защитным слоем” от перегрева поверхности. Удельная мощность электромагнитного ВЧ поля в единице объёма ΨРi, с учётом формулы (11), определяется следующим образом:
Ψ P = ( δ m )2 = 2( H me )2
i σ s σ s ⋅ ( ∆ P )2
[ ber ′ ( m )]2 + [ bei ′ ( m )]2 ber 2( m 2) + bei 2( m 2)
(Вт/м3).
На рис. 5 приведена зависимость удельной объёмной мощности ΨР i , вычисленной по формуле (15) в зависимости от безразмерной поперечной координаты m для средней проводимости σ s = 230 1/Ω·м и напряжённости магнитного поля H me = 9563 А/м на границе конуса, что соответствует току индуктора 71 А, длине конуса индуктора 42 мм и количеству витков N = 4 для индуктора. Глубина скин-слоя равна Δ p ≈ 10 мм для параметра m 2 = 2,9.
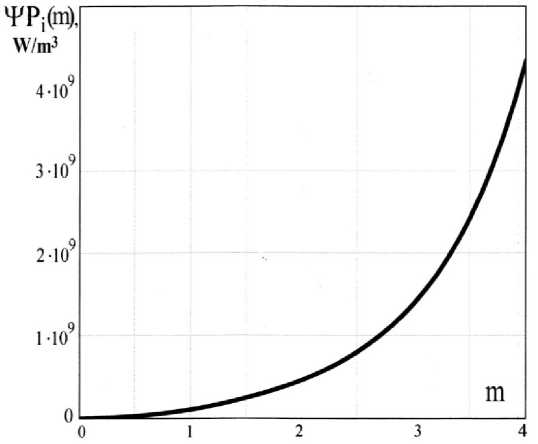
Рис. 5. Расчётная удельная мощность ΨРi(W / m3)в зависимости от безразмерной координаты m для проводимости σs= 230 1/Ω·м
Fig. 5. Estimated specific power ΨPi(W/m3) depending on the dimensionless coordinate m for conductivity σs=230 1/Ω^m
Для эффективного разогрева газов плазмой важным параметром является зависимость от температуры времени их рекомбинации ˂τ ion ˃. Это время определяется физическими свойствами: массой, температурой и средней концентрацией ионов в единице объёма и должно быть не меньше, чем время их пролёта через зону подогрева плазмой τ f ~ 8 мкс. Данное требование соответствует полученным экспериментальным данным для азота, причём ˂τ ion ˃ имеет тенденцию увеличения с ростом температуры с ~1 мкс при Т а = 300 оК до ~ 10 мкс при Т а = 3000 оК для равной концентраций ионов и электронов, около n i ~ 1018 м-3 и давлении ~ 0,1 МПa [13]. Следовательно, время разогрева ионов в азотосодержащей плазме значительно меньше времени их пролёта τ f , а время её «остывания» значительно больше τ f и достигает величины ~ 100 мкс по оптическим измерениям температуры потоков плазмы по выходу из плазматрона [12]. Это важное экспериментальное наблюдение для плазмы чистого азота, но для сложного состава газов, соответствующего нашей работе, экспериментальных данных для ˂τ ion ˃пока не получено.
5. Результаты численного моделирования
Для проведения моделирования необходимо определить основные газодинамические соотношения для расширяющихся газовых потоков в конусном сопле без внешнего подогрева и затем ввести некоторый участок сопла с подогревом газов ВЧ плазмой. Самым важным участком для всего конусного сопла является, естественно, начальный участок, прилегающий к критическому сечению и располагающийся до расчётного сечения, определяющего всю тягу ЖРД. Это обосновано тем, что занимаемый здесь объём под индуктором является наименьшим и поэтому требуется относительно небольшая удельная мощность ВЧ поля для существенного подогрева газов плазмой. В работе [2] приведены основные формулы для расчётов распределения относительной скорости λ = W ( z ) / W cr , распределения давления Р (λ), температуры Т (λ) и плотности газов ρ(λ) вдоль сопла. Здесь W ( z ) – скорость потока газа вдоль оси сопла, W cr – значение скорости в критическом сечении. Приведём эти формулы по данной работе [2]:
f c (λ) = S / S cr = (1/λ)·{(2/(k + 1)) / (1 - λ2·[(k - 1) / (k + 1)]}1/k-1, (16)
где S , S cr – площадь сечения сопла вдоль конуса и в критическом сечении; k = 1,125 – показатель политропического расширения газов в конусном сопле при расчётном давлении P КС = 1 МПа и температуре Т КС = 2949 оК в КС;
Т (λ) = Т cr ∙{1 – [( k - 1) / ( k + 1)]·λ2}, P (λ) = P cr ∙[ T (λ)]k/k-1, ρ(λ) = ρ cr ∙( P / P cr )1/k, (17) где P cr = 0,581 МПa – давление, Т cr = 2816 оК температура, ρ cr = 0,658 кг/м3 – плотность газа в критическом сечении, соответственно. Результаты расчётов газодинамических функций по формулам (16) и (17) и с параметрами раздела 3 приведены в табл. 1. Расчёты удовлетворительно согласуются с данными, приведёнными в работе [3], для смеси керосина с азотной кислотой, которые получены с учётом неполного сгорания топлива в КС.
Параметры расчётных газодинамических функций по длине конического сопла без подогрева плазмой
|
1 R cr |
|||||||||||
|
L, мм |
0 |
5 |
10 |
15 |
20 |
40 |
60 |
80 |
100 |
120 |
150 |
|
R, мм |
5,0 |
5,8 |
6,7 |
7,5 |
8,3 |
11,7 |
15 |
18,3 |
21,7 |
25 |
30 |
|
2 S, мм |
78 |
107 |
140 |
177 |
218 |
428 |
707 |
1056 |
1475 |
1963 |
2827 |
|
F = S/S cr |
1,00 |
1,36 |
1,78 |
2,25 |
2,78 |
5,44 |
9,00 |
13,4 |
18,78 |
25,0 |
36,0 |
|
λ |
1,00 |
1,56 |
1,76 |
1,92 |
2,02 |
2,29 |
2,45 |
2,57 |
2,65 |
2,72 |
2,79 |
|
P, кПа |
581 |
250 |
162 |
115 |
86 |
36 |
20 |
12 |
8 |
6 |
4 |
|
P cr /P |
1,0 |
2,3 |
3,6 |
5,1 |
6,8 |
16,1 |
29,1 |
47,6 |
70,0 |
96,8 |
145,3 |
|
T, оК |
2816 |
2528 |
2409 |
2319 |
2245 |
2038 |
1904 |
1807 |
1732 |
1670 |
1597 |
|
V, м/с |
997 |
1553 |
1758 |
1909 |
2008 |
2284 |
2446 |
2557 |
2640 |
2706 |
2782 |
|
ρ кг/м3 |
0,66 |
0,31 |
0,21 |
0,16 |
0,12 |
0,06 |
0,03 |
0,02 |
0,015 |
0,011 |
0,008 |
Дальнейшие вычисления проводились с применением метода контрольного объёма по работе [5]. Для этого область под индуктором от L1 = 5 мм до области L2 = 15 мм была разбита на 10 неравных объёмов с шагом 1 мм, а все вычисления программы AutoCAD2001 Professional по формулам (1), (3), (5) – (10), (15) – (18) проводились до тех пор, пока величина давления не превышала предыдущее значение не более, чем на 1 кПа. Значения λ вычислялись с точностью не менее 10–6 после запятой, тогда погрешность функций fс(λ), P(λ), Т(λ), ρ(λ) составляла менее 10–4. Удельная поглощённая ВЧ мощность для всего объёма с плазмой Pi = 1,2 ∙ 109 Вт/м3, была выбрана с многократным превышением над удельной тепловой мощностью в камере сгорания с целью нивелировать рассчитанные потери от диссоциации газов (~14,2 Вт/см3), внутреннего трения (~1,3 Вт/см3) и теплопроводности плазмы стенками (~16,5 Вт/см3). Доля поглощённой электромагнитной ВЧ мощности для каждого контрольного объёма определялась с учётом её доли ξi от всего объёма и доли от энтальпии ϑi c учётом зависимостей μа, χа и ср от температуры, причём функции μа~μа(Та) и χа~χа(Та) принимались увеличивавшимися линейно. Решение для всех уравнений находилось при условии, что температура электронов в объёме под витками индуктора составляет постоянную величину Te = const = 3750 ºК, за исключением граничного участка у поверхности сопла. Температура атомов (ионов) Тi(z) определялась в итерационном процессе вычислений. Формулы для расчёта участка плазменного подогрева следующие:
λ с = [1 + λ2+ (λ ni )2]1/2, (λ ni )2= [2 ∙ (Σh i ∙ ξ i ) / (< W cr >)2] · (ϑ i / ∑ϑ i ),
ϑ i = (1/10) · [(Т i - T н ) / T н + (Т i - T i–1 ) / 2 T н )], (18) где (λ ni )2 – составляющая скорости, обусловленная подогревом плазмой, согласно формулам (15)–(17); Σ h i = 11,7 МДж/кг, рассчитанное выше значение для энтальпии плазмы газов; ξ i – доля расчётного объёма от всего объёма плазмы в интервале 5–15 мм, шаг 1 мм (i = 1..10); ϑ i – доля от полной энтальпии для расчётного объёма с температурами на границах объёма T i , T i–1 ; T н = 2528 оК. Начальные условия для расчётов приведены в табл. 1 для значения длины сопла L = 5 мм, а также взяты из работ [3; 5]. В соответствии с методом контрольного объёма [4], определялась плотность газов для каждого контрольного объёма: ρ i = G / (υ i ∙ S i ). Затем вычислялось давление при программном подборе температуры T i : P i = k Б ∙ T i ∙ (ρ i / ˂ M a ˃), где ˂ М а ˃ = 5,3 ∙ 10–26 кг средний вес атомов газов. В табл. 2 приведены результаты расчётов в десяти расчётных объёмах, а также после участка плазменного подогрева. Расчётные значения параметров: мощность, подводимая к индуктору 1,68 кВт; частота ВЧ поля 27,12 МГц. Расчёт для объёмов после участка плазменного подогрева проводился по формулам (16) – (17) с учётом того, что значение длины сопла L = 16 мм, прилегающее к конусу плазменного подогрева считалось новым критическим сечением с R cr2 = 7,6 мм. Фактически получилось, что сечение для R cr2 совпало с расчётным сечением S a = 185 мм2, для которого давление близко атмосферному давлению ~ 0,1 МПa , причём скорость потока газов υ а = 2094 м/с, поэтому можно было вычислить расчётную тягу на уровне моря ~ 108 Н , что больше расчётной тяги без подогрева в 1,064 раза. Предельная полная тяга ~ 185,3 Н, соответствует высоте около 16 км и равна произведению скорости потока в конце конического сопла ( L с = 150 мм) на расход газов G = 0,052 кг/с плюс произведение площади сопла на выходе на выходное давление. Это значение больше тяги без плазменного подогрева на 19 %. Из табл. 1 и 2 следует, что достаточно мощный локальный подогрев газов в коническом сопле приводит к подъёму локальной температуры в 1,22 раза при незначительном изменении давления. Плотность газов становится значительно меньше, чем плотность без локального подогрева, причём температура остаётся достаточно высокой до самого конца конического сопла ~1788 оК при длине сопла L с = 150 мм. На рис. 6 приведены результаты расчётов для скорости и температуры потока газов без подогрева плазмой ( υ c , Т с ) и с подогревом плазмой ( υ р , Т р ) при удельной мощности подогрева плазмой Р i = 1,2 ∙ 109 (Вт/м3) и давлении в камере сгорания 1 МПa .
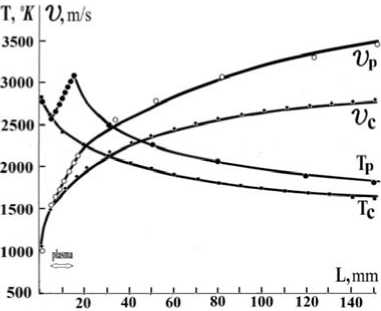
Рис. 6. Зависимости температуры Т с и средней скорости газов υ c вдоль оси сопла без подогрева плазмой и температуры Т р и скорости υ р при подогреве плазмой на длине 5–15 мм
Fig. 6. The dependence of the temperature Tc and the average velocity of gases υc along the nozzle axis without plasma heating and the temperature Tp and the speed υp when heated by plasma at a length of 5–15 mm
Видно, что с ростом температуры увеличивается и скорость потока газов в объёме, подвергнутому подогреву плазмой. Величина такого увеличения определяется энтальпией для газов, которая зависит от подводимой мощности к индуктору и эффективности передачи энергии от индуктора к току электронов, а от электронов потоку газов.
На рис. 7 приведены результаты численных расчётов для температуры газов Т а и электронов Т e на участке подогрева газов плазмой с учётом её изменения в азимутальном и радиальном направлении.
Вдоль стенок сопла температура имеет некоторый экстремум Т max , который плавно смещается к оси сопла вдоль продольной оси z . Наличие данного экстремума объясняется тем, что вектор Умова – Пойтинга для потока энергии электромагнитного ВЧ-поля направлен по нормали от поверхности диэлектрического сопла. Поэтому максимальная плотность энергии будет лежать у данной поверхности, где локальный градиент температур Т а и Т e максимален, что согласуется с расчётами по формуле (14) для удельной мощности ΨР i , показанной на рис. 5.
Предельная температура НТП Т ~ 6000 ºК будет ограничиваться не столько теплостойкостью охлаждаемых стенок из высокотемпературной керамики конического сопла, сколько общим падением эффективности передачи энергии электрического ВЧ-поля в кинетическую энергию потока газов, вследствие резкого возрастания потерь на излучение, что установлено теоретически [7] и экспериментально [14]. Следовательно, при дальнейшем увеличении температуры газового потока, при подводе дополнительной мощности электромагнитного ВЧ-поля, добиться значительного прироста его скорости будет, вероятно, затруднительно.
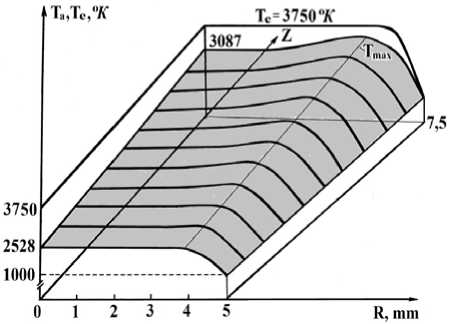
Рис. 7. График 3-D типа для участков от критического сечения R cr = 5 мм и подогрева плазмой с радиусом от 5 до 7,5 мм для температуры газов Т а и электронов Т e
Fig. 7. 3-D type graph for sections from the critical cross-section Rcr=5 mm and plasma heating with a radius of 5 to 7.5 mm for the temperature of gases Ta and electrons Te
6. Основные экспериментальные результаты
Для проведения экспериментов с газовыми смесями, был изготовлен охлаждаемый водой кварцевый реактор, с размерами близкими к разделу 2 и плазмо-газопламенный стенд (рис. 8 и 9). Измерение энтальпии газовых потоков производилось массивной термопарой вольфрам / рений ТВР-251 с молибденовым кожухом. Проводились эксперименты с газовыми, жидкими и комбинированными горючими смесями с массовым расходом до 0,01 кгс/с.
На основании численных расчётов и ряда предварительных физических опытов и экспериментов, был сделан вывод о необходимости модификации топлива на основе керосина со свойством самовоспламенения, а также изготовления специального окислителя нового типа. Этот окислитель с оптимальным составом был изготовлен и испытан в кварцевом реакторе, показав достаточную стабильность физических свойств в течение одного года. Измерительный стенд с генератором мощностью 1,5 кВт на основе двух генераторных ламп ГУ-81М, работавших на частоте 13,56 МГц, позволял проводить измерение средней проводимости сверхзвукового газового потока на выходе из сопла. На данном стенде проводились все необходимые физические эксперименты, которые, собственно, и позволили создать модифицированное топливо со свойствами самовоспламенения при контакте с окислителем нового типа. Эксперименты происходили при максимальной температуре в камере сгорания ~ 2500 оК и давлениях ≤ 0,2 МПa.

Рис. 8. Реактор кварцевый

Рис. 9. Стенд плазмо-газопламенный
Fig. 8. Quartz reactor
Fig. 9. Plasma/gas flame stand
При локальном подогреве НТП сверхзвукового газового потока в коническом, кварцевом сопле, посредством ВЧ индуктора, установлено: температура на выходе из сопла увеличивается до ~ 90 оК, значительно возрастает средняя проводимость газового потока, происходит заметный рост энтальпии всего газового потока. Эффективность подогрева плазмой, по нашей оценке, составляет 8–10 %. Тепловая мощность КС для кварцевого реактора кратковременно достигала 4 кВт и ограничивалась его механической прочностью.
Заключение
Проведённые расчёты показывают, что, для сверхзвукового потока газов в коническом сопле около критического сечения при Т = 2528 – 2752 ºК, проводимость газов является недостаточной для осуществления значительного плазменного подогрева даже при использовании примесей щелочных металлов. Поэтому появляется необходимость использования дополнительной, внешней ионизации газов до расчётной величины дополнительным устройством – ионизатором [15], чтобы скин-слой был соизмерим с радиусом каждого расчётного конического сопла, особенно прилегающего к критическому сечению. Тогда нагрев газов будет носить объёмный характер, а энергия ВЧ поля будет поглощаться достаточно эффективно (~ 70 %). Расчётная температура в области подогрева увеличится с 2319 до 3087 ºК. Произойдёт рост скорости потока газов с 1909 до 2049 м/с. Значит, если удельная мощность при нагреве газов электромагнитным ВЧ-полем значительно превышает удельную (тепловую) мощность для КС, то происходит общий рост скорости газов вдоль сопла, обусловленный локальным подогревом плазмой в ВЧ-индукторе. По настоящему расчёту, для одного короткого индуктора увеличение расчётной тяги на уровне моря, без учёта влияния давления электромагнитного поля, составляло 6,4 % при максимальной энтальпии плазмы ~ 11,7 МДж/кг. Рост полной расчётной тяги на высоте 16 км достигал 19 %, а при увеличении длины сопла может возрасти ещё значительнее. Давление от электромагнитного ВЧ-поля при смоделированных потоках электронов (ионов) незначительно ~ 30 Па, но способно увеличить тягу ЖРД на больших высотах полёта при увеличении тока индуктора.
Таким образом, расчёты и эксперименты показывают возможность подогрева плазмой сверхзвукового потока газов для конического сопла малогабаритного ЖРД. Это позволит в дальнейшем значительно увеличить его удельный импульс вследствие увеличения скорости потока газов в расчётном сечении, а также полную тягу на больших высотах полёта КА, если производить подогрев плазмой газовый поток по всей длине сопла.
Благодарности. Автор благодарит ООО «Аника М» (г. Новосибирск, за всестороннюю помощь и финансовую поддержку при выполнении данной работы.
Acknowledgements. The author is especially grateful to “Anika M” LLC (Novosibirsk, for financial assistance in performing this work.
Список литературы Численное моделирование сверхзвукового потока газов в коническом сопле с локальным подогревом плазмой и результаты экспериментов
- Коротеев А. С., Миронов В. М., Свирчук Ю. С. Плазматроны. М.: Машиностроение, 1993. 296 с.
- Абрамович Г. Н. Прикладная газовая динамика. Т. 1. М.: Наука, 1991. 597 с.
- Термодинамические и теплофизические свойства продуктов сгорания: справочник в 10 т. Т. 5 / под ред. ак. В. П. Глушко. М.: ВИНИТИ АН СССР, 1971.
- Дресвин С. В., Иванов Д. В. Основы математического моделирования плазмотронов. Ч. 2. СПб.: СПб политехн. ун-т, 2006. 292 с.
- Дресвин С. В., Иванов Д. В., Нгуен К. Ши. Основы математического моделирования плазмотронов. Ч. 3. СПб.: СПб политехн. ун-т, 2006. 138 с.
- Васильевский С .А., Колесников А. Ф. Численное моделирование течений равновесной индукционной плазмы в цилиндрическом канале плазмотрона // Известия РАН. Механика жидкости и газа. 2000. № 5. С. 164–173.
- Рожанский В. А. Теория плазмы. СПб., М., Краснодар: Лань, 2012. 320 с.
- Варгафтик Н. Б. Справочник по теплофизическим свойствам газов и жидкостей. М.: Наука, 1972. 720 с.
- Сахаров В. И. Численное моделирование термически и химически неравновесных течений и теплообмена в недорасширенных струях индукционного плазматрона // Известия РАН. Механика жидкости и газа. 2007. № 6. С. 157–168.
- Reid R. C., Prausnitz J. M., Sherwood T. K. The Properties of Gases and Liquids. N.Y.: McGraw-Hill, 1977. 688 p.
- Слухоцкий А. Е., Рыскин С. Е. Индукторы для индукционного нагрева. Л.: Энергия, 1974. 264 с.
- Kolesnikov A. F., Vasil`evskii S. A. Some problems of numerical simulation of discharge electrodynamics in induction plasmatron // Proc. 15th IMACS World Cong.: Berlin, 1997. Vol. 3. Computation Physics. / Ed. by A. Sydow. Wissenschaft & Technic Verlag. P. 175–180.
- Шибкова Л. В. Физические процессы в движущейся плазме многокомпонентных инертных и химически активных смесей: автореф. дис. … д-ра физ.-мат. наук. М.: МГУ им. М. В. Ломоносова, 2007. 43 с.
- Voronin S. T. Numerical simulation of supersonic gas flow in a conical nozzle with local plasma heating // Technical Physics Letters. 2022. Vol. 48, No. 5, P. 62–66.
- Воронин С. Т. Ионизатор горячих газовых потоков высокой плотности рентгеновским, характеристическим излучением при фотолюминесценции комбинированного анода трансмиссионного типа // Физические основы приборостроения. 2022. Т. 11, № 3(45). С. 14–21. DOI: 10.25210/jfop-2203-014021.


