Численное моделирование температурных полей тел сложной формы на принципе диакоптики

Рассматривается подход к решению нелинейных многомерных задач теплопроводности конструкций промышленных объектов на принципе диакоптики - решение сложных задач по частям. Конструкция сложной формы представляется комбинацией фигур-примитивов, для которых разработаны простые программные модули. Сопряжение модулей происходит через граничные тепловые сопротивления фигур на основе полученных обобщенных зависимостей. Приводится алгоритм решения задачи.

Решение задач теплопроводности для тел, имеющих сложную пространственную форму и переменные краевые условия теплообмена, требует значительных затрат труда и времени. Одним из действенных способов сокращения трудозатрат является использование принципа диакоптики, когда решение одной сложной задачи заменяется решением более простых задач [1]. Рассмотрим один из вариантов такого подхода.

Большинство конструктивных элементов и узлов энергетических установок и различных теплотехнических устройств являются замкнутыми пространственными телами, которые могут быть образованы путем «объединения» простых фигур-примитивов: параллелепипедов, призм, цилиндрических и сфероидальных элементов, тетраэдров, октаэдров и т.д. Число разновидностей таких фигур невелико, часто не превосходит десятка. Составить программы расчета для них значительно проще, чем для всей конструкции. Единожды созданные и отлаженные программы-модули таких фигур могут в дальнейшем многократно использоваться при расчете теплового состояния тел различного конструктивного исполнения.

Решение задачи начинается с построение структурной модели исследуемой конструкции. Она условно расчленяется на фигуры-примитивы (пространственная декомпозиция). Принцип расчленения показан на рис. 1. Изображенная конструкция может быть представлена комбинацией четырех типов фигур: А, В, С и D. Каждой фигуре присваивается ее порядковый номер и признак класса, определяющий его тип (форму). Эти данные в совокупности с размерами фигур являются входными параметрами структурной модели изучаемой конструкции.

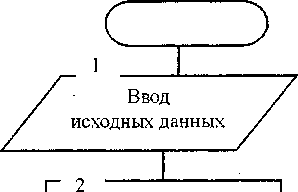
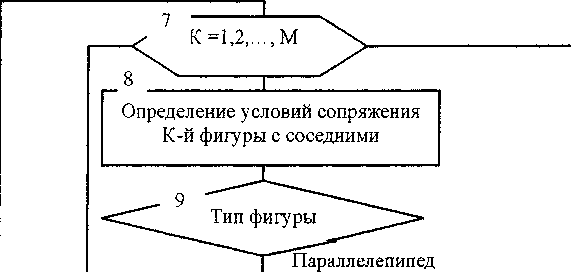
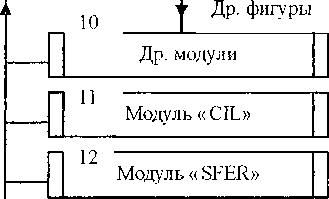
На следующем этапе решаются задачи теплопроводности каждой фигуры с последующей операцией синтеза их тепловых полей. Алгоритм численного расчета нестационарного температурного поля конструкции произвольной формы представлен на рис. 2. Входные данные включают геометрические и топологические параметры фигур, их теплофизические характеристики, граничные ус ловия теплообмена и числовой массив управляющих признаков. Блок 4 открывает временной цикл расчетной схемы, начинающийся временным счетчиком т = т + Дт. Здесь Дт - временной шаг, который может изменяться во времени или оставаться постоянным. Основная часть алгоритма включает блоки 7-15. Блок 7 организует цикл расчёта теплового состояния по каждой из М фигур. В блоке 8 определяются условия сопряжения К-й фигуры и формируются граничные массивы температур. В зависимости от типа фигуры (блок 9) вызывается соответствующий тип модуля: PAR (расчет параллелепипеда), PRJZ (расчет призмы), SFER (расчёт сфероидального элемента), CIL (расчёт цилиндра). В архив модулей могут входить другие подпрограммы (блок 10). Блок 15 проверяет условие сходимости итерационного процесса для каждой фигуры. Вывод расчетной информации регламентируется блоком 16, где Дтв-.очередной момент вывода расчетных данных. После работы блока 17 проверяется условие окончания счета по конечному времени процесса 7К. Если условие не выполняется, то значение 7В увеличивается на временной шаг вывода Дтв.

Ключевым местом в реализации рассматриваемого подхода является вопрос о сопряжении отдельных фигур между собой. Важную роль в решении этого вопроса играет выбор метода расчета теплового состояния фигур. Расчетная схема метода должна быть достаточно универсальной и учитывать различия формы переноса энергии как на границе, так и внутри фигур, а также отвечать характеру сопряжения фигур. При использовании традиционных методов конечных разностей или конечных элементов сопряжение возможно осуществить лишь через общие граничные расчетные точки сеток разбиения стыкующихся фигур. Это обстоятельство вызывает необходимость привязки сеток, что существенно ограничивает возможности методов.

Перечисленным выше требованиям в наибольшей степени соответствует одна из модификаций метода элементарных тепловых балансов

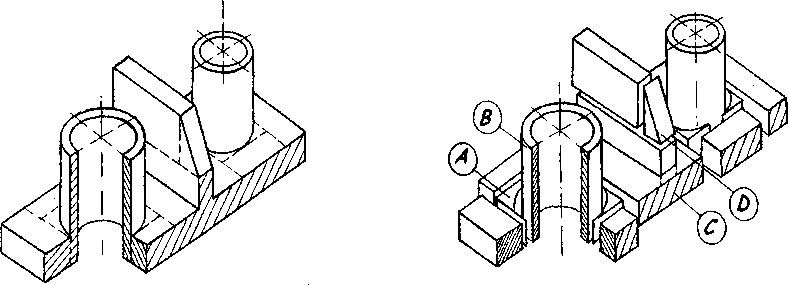
Рис. 1. Пространственная декомпозиция узла

[2]. Единый подход к анализу сложных тепловых явлений с общих принципов закона сохранения и превращения энергии делает его универсальным и в то же время простым и доступным широкому кругу специалистов. Численная модель метода основывается на приближенном интегрировании уравнения баланса энергии jqnUW+jqvdy=[pCp^dy, (1) F V V записанного для произвольного тела объемом У. Первое слагаемое определяет тепловой поток, проходящий через поверхность тела. Здесь q„ (А)-проекция вектора плотности теплового потока на нормаль и в точке A (A С F). Вторым слагаемым учитывается действие внутренних источников тепла мощностью q,. Интеграл в правой части уравнения (1) определяет изменение энтальпии тела во времени т.

Для расчета теплового состояния тело условно разбивается на достаточно малые объемы так, чтобы можно было считать температуру и мощность внутренних тепловыделений в них одинаковыми и постоянными в течение некоторого промежутка времени Ат. Температура определяется в узловых точках, лежащих внутри объемов разбиения. Таким образом, сопряжение фигур происходит не через узловые точки, а посредством контакта границ ячеек пространственной сетки. Модель теплообмена между фигурами получается адекватной модели передачи тепла между ячейками сетки. Задача сопряжения практически сводится к расчету тепловых сопротивлений между поверхностными ячейками разбиения стыкующихся фигур.

Методика определения тепловых сопротивлений сетки разбиения основывается на следующих допущениях. Примем в качестве структурной модели передачи тепла между двумя сопряженными ячейками двухслойную стенку.

Слоями являются части ячеек (объемов) от границы их сопряжения до эквидистантных ей изотермических поверхностей, проходящих через узловые точки с температурами 7) и Г2 на расстояниях А] и Иг соответственно. Тогда тепловое сопротивление между узловыми точками будет эквивалентно тепловому сопротивлению стенки и определится из уравнения Фурье

Q = -X(T)dT/dn F(n).

После разделения переменных

QIF^-dn = -ЦТ) dT и интегрирования в границах г-го слоя

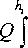
dn

тк

= -]X,(T)dT т.

получаем

% dn

' F, (и)

С другой стороны, тот же тепловой поток равен

Q = (T,-Tk)fR1.

Из двух последних соотношений определяется величина теплового сопротивления z-ro слоя r, =(т, -та—-----

VatW тк или

Аналогичным образом можно получить зависимость теплового сопротивленияу-го слоя:

h;

г dn

о ^FjW

/ 'Rj ср •

Горбенко В.И.

Численное моделирование температурных полей тел сложной формы на принципе диакоптики

Блок защиты данных

Призма

Задание начальных условий

Сфера

Счетчик времени процесса Т

Г 5  -----------

Расчет временных граничных условий конструкции

Цилиндр

Модуль «PRIZ»

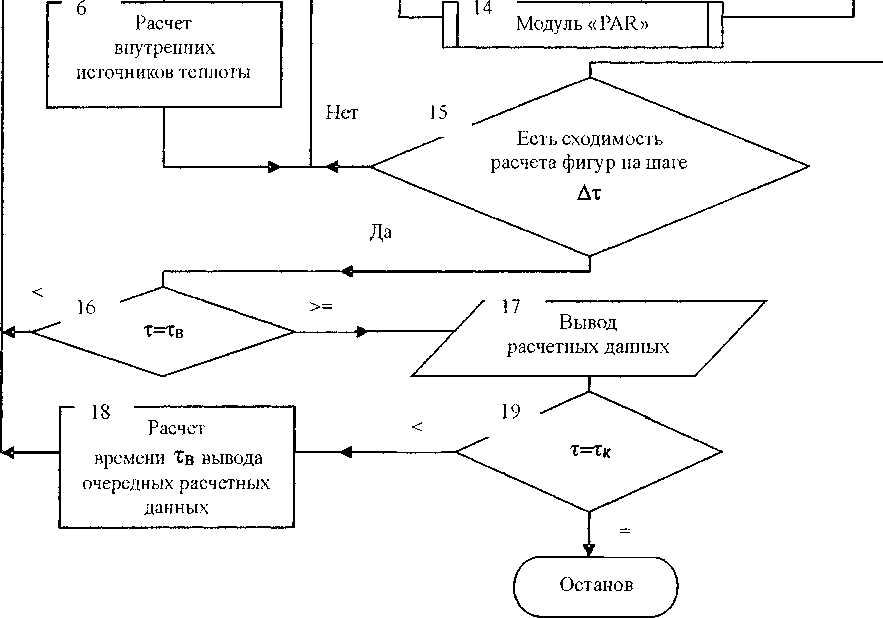
Рис. 2. Алгоритм решения задач нестационарной теплопроводности по принципу диакоптики

Полное внутреннее тепловое сопротивление между двумя соседними ячейками сетки в n-м направлении и величина теплового потока составит где

R,j - Ri + Rj-

• 1    % dn 1 r dn Кр^П^ ^jcpVj^V

Xlcp= ^T)dTl(T,-TK)> В ......

Tk

Xjcp= \Х^Т/(ТК-Т}).

На основе изложенного подхода разработан алгоритм и вариант программы расчета нестационарных температурных полей конструкции в граничных условиях 1-го и 3-го рода. Использование принципа диакоптики в решении задач теплопроводности конструкций сложной геометрической формы существенно сокращает объем работ по моделированию на ЭВМ их теплового состояния.