Численное моделирование термо-напряженного состояния стержня в виде усеченного конуса

Существующие методы исследования установившегося термомеханического состояния стержней ограниченной длины не позволяют учесть зависимость между коэффициентом теплового расширения и полем распределения температуры, условия эксплуатации и закрепления. К текущему моменту не разработана математическая модель установившегося термомеханического состояния стержней при вышеотмеченных условиях работы конструктивного элемента. Определяющие соотношения термоупругости слабо сжимаемых материалов рассмотрены в [1]. Для записи кинематических соотношений использовано разложение градиента места на силовую и температурную составляющие. Сжимаемость (или не сжимаемость) материала определяется обобщенным модулем упругости, по величине которого можно судить о степени сжимаемости материала. В [2] рассматривается проблема прочностного расчета самокомпенсирующихся трубопроводов, уложенных в грунт, при нагреве. Полагается, что компенсация температурных удлинений происходит за счет изгибных деформаций трубопровода в упругой среде с соответствующим коэффициентом жесткости. Обзор результатов (полученных в последнее время) о точной и приближенной управляемости и стабилизации в системах с распределенными параметрами, описывающими процессы управляемости и стабилизации в теориях упругости, теплопроводности и термоупругости, рассмотрен в [3].

В [4] описываются выдвигаемые тонкостенные стержни, используемые на космических аппаратах в качестве удлинителей для различных грузов и приборов, а также штанг гравитационной стабилизации. Рассмотрена связанная нелинейная задача сильного термоупругого изгиба и теплопроводности тонкостенного круглого стержня с учетом внешнего и внутреннего теплоизлучения и получено ее численное решение. Задача об определении температурных напряжений в трехслойной системе рассмотрена в [5]. Алгоритм расчета температурных напряжений и деформаций в круглых упругих элементах в виде трехслойных пластин, состоящих из жестких слоев, выполненных из разнородных материалов и соединенных между собой промежуточным слоем, работающим на сдвиг, исследован в [6].

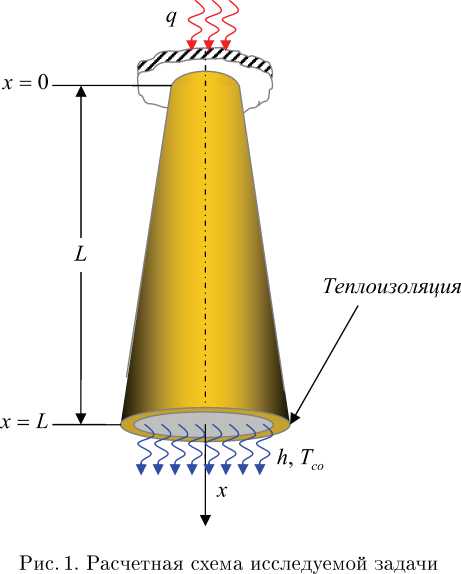
Предположим, дан вертикальный стержень переменного сечения и ограниченной длины L (см). Верхний конец его жестко защемлен. Ось O x совпадает с осью исследуемого стержня, направим ее сверху вниз. Боковая поверхность стержня теплоизолирована. Радиус стержня r (см) по направлению оси меняется линейно, т. е. r = ax + b, где а и b — постоянные числа. Если радиус стержня на верхнем конце (при x = 0) обозначить через r₀, ана нижнем конце (x = L) через r_L, то имеем, что

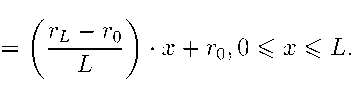
Тогда значение площади поперечного сечения стержня зависит от координаты x нелинейно

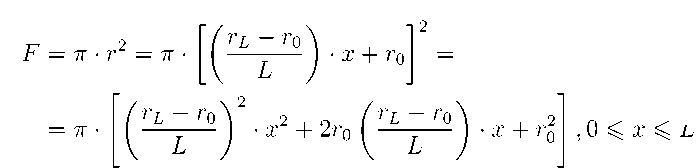
F = п • r2 = п x + r2 , 0 6 x 6 L.

Пусть на площадь поперечного сечения верхнего защемленного конца (x = 0) стержня S0 = п • r2 подведен тепловой поток q (В т/с м2). Через площадь поперечного сечения нижнего (x = L) конца стержня S L = п • r L происходит теплообмен с окружающей ее средой. При этом коэффициент теплообмена — h (В т/(с м2 • ° С)), а температура окружающей среды — Tco (°C>) (рис. 1).

Требуется определить поле распределения температуры по длине стержня переменного сечения, а также величину удлинения за счет температурного распределения.

Эту задачу решим, пользуясь законами сохранения энергии. При этом сначала ее решим приближенно-аналитическим методом. Для этого поле распределения температуры по длине рассматриваемого стержня переменного сечения аппроксимируем полным полиномом второго порядка

T = T (x) = ax² + bx + c = ^i(x)Ti + y j ( x ) T j + ^ k ( x ) T k , 0 6 x 6 L

где

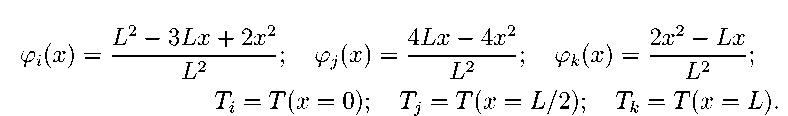
L2 — 3Lx + 2x2      , , 4Lx — 4x2

2x2 - Lx

Ak(x) =

T i = T (x = 0);   T j = T (x = L/2);   T k = T (x = L)

Теперь напишем выражение функционала, которое характеризует полную тепловую энергию исследуемого переменного сечения стержня ограниченной длины [7, 8]

I = / ^ ( dT Т dV + / qTdS + / h ( T - T co )2 dS, v ² \ dx          So           S l 2

где V — объем стержня переменного сечения; S_o — площадь поперечного сечения верхнего защемленного конца (x = 0) стержня, куда подведен тепловой поток q; S_L- площадь поперечного сечения нижнего конца (x = L) стержня, через которую происходит теплообмен.

Как известно, объем усеченного конуса определится следующим образом

V = 3 (r⁰ + Го r L + rL) • nL.                               (5)

Градиент температуры определяется из (2)

dT = ^ilx) + djx) + Э^ к ^(x) = ⁴x - 3L T + 4L - 8x T + 4x ^- L ,T       ₍6)

Пользуясь соотношениями (4) и (6), из (4) получим интегрированный вид функционала (4):

+

h

L 2^

-

T co ) 2 dS

SKL x (^

- 16Ti T j + 2 T i T k - 16Tj T k + 16 T j 2 + 7T_k²)+

+ qSoT i + hSL ( T k - T co )2,

где S = 3(r2 + ro t l + rL); So = n • r0 ; S l = n • rL-

Далее, минимизируя функционал I по узловым значениям температуры, получим следующую систему разрешающих уравнений:

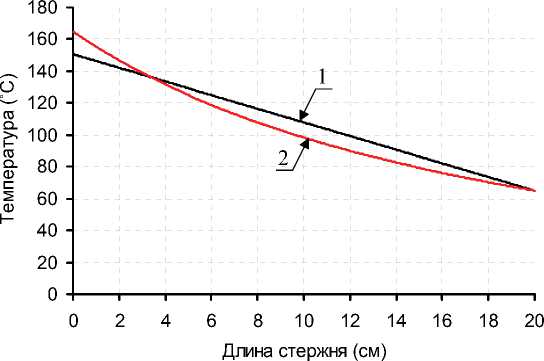
Рис. 2. Поле распределения температуры по длине стержня переменного сечения: 1 — приближенно-аналитическое решение; 2 — численное решение с погрешностью

• 1)    II = 0; ^ S-Kxx (14Ti - 16T + 2Tk) + q • So = 0; OT i

• 2)    II = 0; ^ S-Kxx(-16T - 16Tk + 32T) = 0;>

  
  

dT j

• 3)    = 0; ^ S-Kxx (2Ti - 16T + 14Tk) + h^S L (2T_k - 2TJ = 0.

dTk           6L                             2>

Здесь следует отметить, что во всех скобках сумма коэффициентов перед узловыми значениями всегда будет равно нулю.

(14 - 16 + 2) =0;

(-16 - 16 + 32) = 0;

(2 - 16+ 14) +(2 - 2) = 0.

Решая систему (8), определим узловые значения температуры

T. = T	qS0	qLS0
		;
T j = Tco -	hS L - qS0	xx qLSo ,
	hS L	2SKxx ;
	qS0
T k = T oc -
	hS L .

Подставляя (9) в (2), определим закон распределения температуры по длине исследуемого стержня переменного сечения:

q`S0    qS0      qS0

^T = T^(x) = I To ^- -—    -у- I ⁺      • x, ^{0 6} x ⁶ L.

S K _xx  hS L    SK _xx

Отсюда видно, что в этом случае закон распределения температуры по длине стержня переменного сечения имеет линейный характер. Тогда градиент температуры будет постоянной величиной, т. е.

∂T ∂x

qS0 SKxx

,0 6 x 6 L.

Примем следующие исходные данные: L = 20 см; r₀ = 1 см; r _L = 2 см; K xx = 100 B/(cм^ °C v): q = -1000 B/c м2: h = 10 B/(c м2 • °C v): T co = 40 °C: E = 2 • 106 к Г/см². Коэффициент теплового расширения материала стержня а = 125 • 10-7 1/°С.

При этих исходных данных имеем

T = 150,714 °C ^; T j = 107,857 °C ^; T k = 65 °C С

Тогда закон распределения температуры по длине исследуемого стержня переменного сечения имеет следующий вид

T (x) = 150,714 —7 • x, 0 6 x 6 L = 20 см.

Тогда площадь ограниченной координатными осями От и Ох, а также прямой T(x) =

150,714 — 7 • x оудет равна

St

T1

= Z T (x)dx

= 2157,14 °Cх см.

Величина удлинения исследуемого стержня будет

∆`T1

=     а • T (x)dx

= 2157,14 • 125 • 10-7 = 0,02696 см.

Здесь следует отметить, что полученное аналитическое решение T = T (x) является относительно приближенным. В целях исследования погрешности полученного аналитического решения теперь данную задачу решим численно. Для этого исследуемый стержень дискретизируем 2, 4, 8, 10, 100, 200, 300 квадратичными элементами, каждый раз полученные численные решения сравниваем с приближенно-аналитическим решением. Эти сравнения приводятся в сравнительной таблице. В этой таблице видно, что полученное приближенно-аналитическое решение будет завышено всего на 3,919 % от численного решения с погрешностью 0 %.

На рис. 2 приводится разница между приближенно-аналитическим решением и численно-точным.

Таким образом, выяснили, что во многих инженерных расчетах можно пользоваться удобным приближенно-аналитическим решением.

Теперь в этом примере предположим, что оба конца рассматриваемого стержня переменного сечения жестко защемлены. В связи с этим в нем возникают сжимающее усилие и напряжение (рис. 3).

Для того чтобы найти величину сжимающего усилия R, сначала вычислим осреднен-ную величину площади поперечного сечения. Площадь поперечного сечения левого конца стержня будет F0 = п • r0 = п, а правого конца F L = п • rL = 4п. Тогда вычисляем арифметическое среднее значение площади поперечного сечения. Каждое значение площади поперечного сечения определяется по формуле (1).

Тогда предполагая, что один конец стержня свободен и на нем приложено сжимающее усилие R, по закону Гука определим величину укорачивания исследуемого стержня из-за сжимающего усилия R:

Сравнительная таблица.

Таблица

№ варианта	Число дискретных элементов	Площадь S t (оС х см)	Величина удлинения стержня ААт (см)	Разница, в %
1	1	2157,1428	0,026964	100,00
2	2	2102,2759	0,026278	97,45
3	4	2080,9040	0,026011	96,46
4	8	2074,7349	0,025934	96,18
5	10	2073,9677	0,025924	96,14
6	100	2072,6026	0,025907	96,08
7	200	2072,5921	0,025907	96,08
8	300	2072,5902	0,025907	96,08

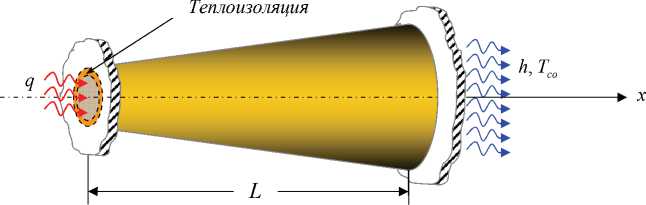
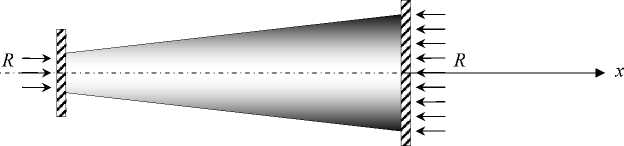
Рис. 3. Расчетная схема, защемленного двумя концами стержня переменного сечения

A' r =

RL

ef

где F cp — арифметическое среднее значение площади поперечного сечения.

Но из-за условия совместности деформации для защемленного двумя концами стержня переменного сечения должно быть

A ' r + Л'т = 0.

Подставляя (10) в (11), получим ERL + Л'_т = 0, отсюда имеем ср

Л'т • E • F_cp —

В нашем примере при принятых исходных данных получим

-7000 J

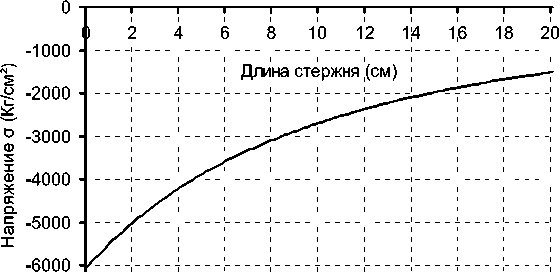
Рис. 4. Поле распределения напряжений по длине стержня переменного сечения

R = — 0 , 025907 • (2 210 6 ) • 7330376 = — 379816 , 118 = -^ _

Следует отметить, что если площадь поперечного сечения исследуемого стержня была, бы постоянной и F = п • г² = п, то величина сжимающего усилия была бы

R = -    9           =         .

20                        ,

Значения термоупругого напряжения в любом сечении рассматриваемого стержня переменного сечения определяются в соответствие с законом Гука:

R ff(x) = F(x)'

где F (x) определяется формулой (1). В частности,

a(x = 0) = ———- =     = -6044,959 к Г/см2;

^{v 7}    F (x = 0) п • r0            ^{, z} ’

a ( x = L/2) = a ( x = 10) = ——   = —Д = - 2686,648 к Г/см²;

F ( x = 10) п • r2

a(x = L) = _a ( x = 20) = ——--- = —Д = -1511,239 к Г/см².

F (x = 20)    п • r L

Теперь, пользуясь соотношениями (17) и (1), можем построить поле распределения термоупругого напряжения по длине исследуемого стержня переменного сечения (рис. 4).