Численное моделирование упругопластического поведения меди в плоской волне сжатия

In the present work, the evolution of the elastic-plastic wave profile is investigated. A mathematical model is constructed to describe the main features of elastic-plastic wave propagation in copper taking into account the non-linear behavior of the ensemble of interacting microshears.

Многочисленными экспериментальными исследованиями показано, что важными дефектами структуры, определяющими релаксационные свойства и кинетику разрушения реальных материалов, являются микросдвиги, микротрещины – типичные дефекты мезоуровня. [1-6]. Так, многочисленные структурные исследования процессов нагружения с различными скоростями указывают на определяющую роль в явлениях пластического деформирования согласованного поведения ансамбля этих микродефектов. В данном исследовании построена математическая модель, описывающая основные черты пластического деформирования при высокоскоростном нагружении с учетом нелинейного поведения ансамбля взаимодействующих микросдвигов.

Значительное внимание вопросам природы пластической деформации уделено в работах научного направления, возглавляемого академиком В.Е.Паниным [7–9], в которых развивается представление о деформируемом твердом теле как о многоуровневой системе, в которой пластическое течение развивается как последовательная эволюция потери сдвиговой устойчивости на различных масштабных уровнях: микро, мезо и макро.

В данной работе используется ранее разработанная теория [10–12], в которой методами статистической физики и термодинамики необратимых процессов изучается влияние микросдвигов на упругие и релаксационные свойства твердых тел. Определяющие уравнения сред с микросдвигами имеют следующий вид:

σ _ik = L ₁ e _i ^p _k - L ₂ p & _ik , Π _ik = L ₂ e_i^p_k - L ₃ p & _ik ,                            (1)

Здесь pik – тензор, характеризующий интенсивность и преимущественную ориентацию микросдвигов;

Π

=∂F ik       ∂pik

–- термодинамическая сила, действующая на систему,

когда p_ik отличается от равновесного ( F – свободная энергия среды с микросдвигами);

σik, eipk – тензоры напряжений и скоростей пластических деформаций; Li – кинетические коэффициенты, зависящие от pik . Определяющие уравнения материала (1) включают соотношения релаксационного типа для тензора напряжений и уравнения движения для параметра pik . В этих уравнениях учтены "перекрестные" эффекты: влияние микросдвигов на релаксационные процессы и пластичности на кинетику роста pik . В дальнейшем рассматривается случай, когда пластическая деформация подчиняется условию e^ = 0 (пластическая несжимаемость материала), а среднее 1

напряжение о = 3 о ii определяется через упругие составляющие тензора деформаций.

В рамках данной теории были определены характерные реакции материалов на образование дефектов.

Рассмотрим пластину меди, у которой два размера по x и по y гораздо больше размера по z . Поэтому, используя гипотезу о плоском деформированном состоянии

8 =8 = 0

xx yy и вводя изменение объема

8=8 +8 +8 , xx yy zz ,

получаем 8 = 8 _zz . Принимая, деформации малы, имеем

что в волнах напряжений умеренной интенсивности

58 zz = 5 vz где vz – скорость по z .

Записывая уравнение неразрывности

58 = 5 v z

5t уравнение движения для случая плоской деформации

5 v. до77 р _z = zz, д t5

используя закон Гука оzz = X8 + 2G8ezZ , о = X8 + 2G8e, xxxx

О yy = X8 + 2 G 8 eyy , где X - первая постоянная Ляме, G - модуль сдвига, 8 - объемная деформация, о = K 8, где о - среднее напряжение, K - модуль объемного сжатия,

. 2 _

K = X + gG ,

^О Zz

= о zz - о ,

где оZz - компонента девиатора тензора напряжений, получаем о' = о — о=X8 + 2G8ez -K8 = X8 + 2G8ez-I X + -G Is=X8-X8 + 2GI 8" — 8 I, zz zz                     zz                        zz           3                                zz 3

о'_г= 2 G I 8 e_z - ¹ 8 I .                                  (9)

zz           zz ₃

Используя представление о малости деформаций, для упругопластической среды имеем ep 8 zz 8 zz + 8 zz , где 8zz, 8ezz, 8Pz - суммарная, упругая, пластическая деформации.

Отсюда

g’,, = 2 G I 8__ --8-8 p | . zz            zz            zz

Используя уравнение (9), справедливое для любого напряженного состояния для плоской волны, с учетом (3), (4) запишем

^ = 2 G [ 2 'v z -8 p_z ) .

5 t        ( 3 5 z     ^zz )

Вводим удельный объем

V = Р о / P ,                                 (12)

где p o - начальное значение плотности, p - текущее значение плотности Уравнение неразрывности приобретает вид

£ d V _ d v _z

V 9 t ~dz '

Используя уравнения (5), (7), (11), (12), запишем

Po dvz = 8gzz v a t    az ’

8g'_zz       1 2 a v .p)

zz- = 2 G - 8 p , a t ( 3 a z     ^zz )

dG=K d vz at      az

Уравнения ,описывающие пластические свойства среды, имеют вид

GB = 48pzz -12 'pzz,(17)

zz 1 zz 2

a t

П= = 128P -l3 %.(18)

a t

Динамическое воздействие на пластину описывается граничным условием gzz (0, t) = f (t),(19)

где f ( t ) – функция, описывающая импульс нагрузки формы, близкой к прямоугольной. Тыльная сторона пластины свободна от нагрузки,

Gzz (h, t) = o.(20)

Система должна удовлетворять начальным условиям

Vz (z,0) = Gzz (z,0) = Pzz (z,0) = 0,(21)

z e [0,1], t e [0,го), здесь p - плотность материала; t - время; z - пространственная координата; vz - компонента вектора скорости; gzz, Gzz, 8zz, 8pzz, pzz - компоненты тензоров напряжений, девиатора напряжений, скоростей деформаций, скоростей пластических деформаций, параметра плотности микросдвигов; g - среднее напряжение; K - модуль объемного

,                                        , , ,                                   1                      ,        8F сжатия, h - толщина пластины,. 11,12,13 - кинетические коэффициенты, Пzz =----, где дPzz

F – свободная энергия.

Обезразмерим систему (13) – (21). Введем безразмерные параметры а = G zz G ’ t = —, где At = L / G,

A t             1

z z = h ’ где h – толщина пластины,

V =

v _zz l ₁ hG ^,

П zz

U'

G

Получаем систему уравнений в безразмерном виде
5 v       Sczz — = a V—zz- , 5 1        d z	(22)
1 d V д V	(23)
V 5 1    d z ,
6g'zz  V 4 5 V - ) zz ^ , д t     ( 3 5 z     p J	(24)
1 2 5 p„ £„ =G'+ — -^z-p zz    1 1   5 1	(25)
= l 2 IE -n‘ , 5 1    1 3 p	(26)
5g = K 5 V	(27)
5 1    G 51 ’
g zz =g'zz + g ,	(28)
l 2                               l где a = —1—y , П = A t - П = — П = 1x П . 2                     zz           zz 1 zz p 0 Gh              G
Функция П' аппроксимировалась выражением

^П' = ^- A "^ zz • ^exP^{( -} P a / P zz ) + B ⁽ P zz ^- P b ),                         ⁽²⁹⁾

.

где A , B , p _a , p _b – параметры аппроксимации.

Численное исследование системы (22)–(29) проводилось методом конечных разностей. Использовались следующие значения констант для меди:

p = 8,6 - 10 3 кг/м³, E = 1,12 - 10 11 Па, G = 0,408 - 10 11 Па,

1₁ = 1,0 • 10 5 н^с, 1 ₂ = 0,45 - 10 5 н-с, 1 ₁ = 1,0 - 10 5 н^с,

А = 57,0, B = 0,25 - 10 ^{- 2} - A , p a = - 1,5 - 10 ^{- 3}, p b = - 1,5 - 10 ^{- 4} .

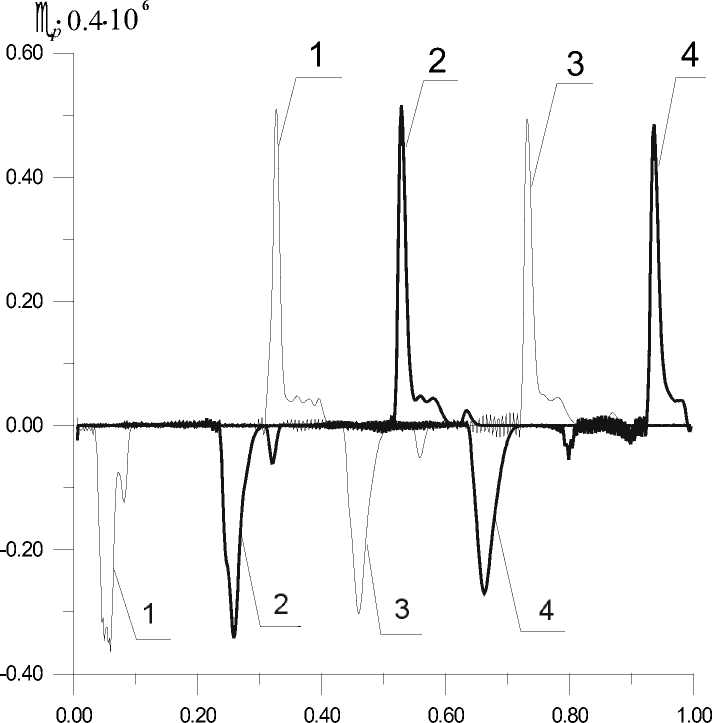
На рис.1,2 приведены результаты численного моделирования распространения волн напряжений при амплитуде нагружения σ ₀ = 3,0 ⋅ 10⁹ Па, длительности импульса Δ t ₀ = 3,675 ⋅ 10 ^{- 7} с, толщине медной пластины h = 5,0 ⋅ 10 ^{- 3}м.