Численное моделирование влияния пары наночастиц на электромагнитное поле в ближней зоне методом векторных конечных элементов

Нанокомпозиты с частицами восстановленных металлов находят широкое применение в качестве оптоэлектронных элементов, оптических сенсоров, приборов для регистрации оптических сигналов, оптических наноантенн и пр. [1]. Данные материалы представляют собой сложные структуры, содержащие огромное число диэлектрических и металлических наночастиц [2–4]. Исследование их оптических свойств представляет собой сложную и трудоёмкую задачу, решение которой целесообразно осуществлять посредством математического моделирования на основе метода декомпозиции. Такой подход позволяет рассматривать процессы взаимодействия электромагнитного излучения оптического диапазона как с отдельными наночастицами диэлектриков и восстановленных металлов, так и с их ограниченными ансамблями, а затем обобщить результаты на весь материал в целом.

В настоящее время всё большее распространение получают композиционные SiO 2 -материалы, структурированные ионами металлов или наночастицами восстановленных металлов [2]. Благодаря присутствию пространственного наномасштаба вещества в этих материалах может происходить локализация и усиление оптических полей. Кроме того, по своей природе металлические наночастицы обладают собственными колебаниями с частотами в оптической области от ультрафиолетового до инфракрасного диапазонов [3, 5].

Значительную часть времени при разработке и синтезе подобных материалов занимает производство и изучение их прототипов. Натурные эксперименты

позволяют провести физические измерения оптических свойств [6, 7].

Основным объектом исследования является электромагнитное поле, по распределению которого можно судить об оптических и других важных физических свойствах конкретного тела. Использование на этой стадии компьютерного моделирования в перспективе позволит перейти к созданию новых материалов с заданными свойствами в виртуальном пространстве до проведения натурных экспериментов, что значительно снизит затраты и ускорит процесс их получения [8].

Моделирование распределения электромагнитного поля сводится к решению уравнений Максвелла (J.C. Maxwell) [3, 5]. В настоящее время для решения данной задачи существует ряд численных и аналитических методов [3– 16], базирующихся на двух основных подходах. Первый основан на решении уравнений в их дифференциальной форме. Данная группа методов позволяет хорошо учитывать сложную, гетерогенную структуру композитного материала, однако при моделировании в бесконечных или частично ограниченных пространствах применение этих методов приводит к значительным вычислительным затратам. Второй подход основан на решении уравнений Максвелла в интегральной форме.

Достаточно часто используются модифицированные методы расширения теории Ми (рассеяние на единичной сфере) для множественного рассеяния на сферах [17 – 20].

Основными численными методами, применяемыми для решения уравнений Максвелла, являются: метод приближения дискретных диполей (DDA) [14, 21], ме- тод нулевого поля (NFM) [10, 21], метод T-матрицы [13, 22], метод граничных элементов (BEM) [23], метод конечных элементов (FEM) [9, 15, 16, 24], метод конечных разностей во временной области (FDTD) [8, 12]. Существует множество работ, посвящённых сравнительному анализу данных методов [8– 11, 20].

В настоящее время практически все методы реализованы в виде программного продукта, причём на каждый метод имеется множество реализаций [9, 10, 25]. Например, метод DDA реализован в пакете DDSCAT [10], метод NFM – в пакете NFM-DS [10,21], метод Т-матриц – в пакете MSTM [22], метод FDTD реализован в пакете Meep [26] и т.д.

Наибольшую популярность и распространение получил метод FDTD. Однако при исследовании распределения электромагнитных полей в композитных материалах на основе высококремнеземных стекол, синтезированных золь-гель методом, и сферических наночастиц восстановленных металлов (на примере Ag, Cu) имеется ряд сложностей, связанных с особенностями метода конечных разностей. Во-первых, размеры шага дискреционной сетки должны быть значительно меньше длины волны, а расчётная область зачастую выходит из наномасштаба, что, в конечном итоге, приводит к необходимости где-то хранить, а затем и решать систему линейных алгебраических уравнений большой размерности (порядка 107). Процесс решения одной подобной системы на вычислительном кластере занимает несколько суток [8]. Это фактически делает невозможным одновременное исследование полей как в «ближней» зоне, так и на значительном расстоянии от источника. Во-вторых, восстановленные металлические частицы имеют сферическую форму, а также содержат выщербины, «пещеры», пустоты [2], что практически невозможно учесть, используя FDTD.

Метод конечных элементов позволяет частично преодолеть указанные недостатки за счёт использования конечных элементов различного размера. Для ближней зоны и самих частиц – более мелкие (размером гораздо меньше длины падающей волны), а для дальней зоны – большего размера. Это позволяет в целом получать систему линейных алгебраических уравнений значительно меньших размерностей для тех же самых задач, чем в методе FDTD. И, в конечном итоге, значительно ускорять время нахождения решения. При использовании разнородных конечных элементов является актуальной задача обеспечения непрерывности напряжённости электрического поля на границах между элементами. Поэтому необходимо найти такие функции формы, которые обеспечивали бы непрерывность напряжённости электрического поля как в «ближней» зоне наночастицы, так и в «дальней».

1. Постановка задачи

Рассмотрим золь-гель стекло, содержащее наночастицы восстановленных металлов [2]. На материал падает плоская монохроматическая волна. Воспользуемся методом декомпозиции и будем определять распределение электромагнитного поля, возникающе- го в ближней зоне пары наночастиц. Начало координат поместим на равном удалении от центра двух частиц. В расчётной области выделим принципиально отличающиеся элементы: частицы, «ближнюю» и «дальнюю» зоны для частиц, полностью поглощающий слой (рис. 1). В качестве граничных условий воспользуемся условиями поглощения (ABC – absorbing boundary condition), реализованными в виде условия излучения Зоммерфельда (A. Sommerfeld)

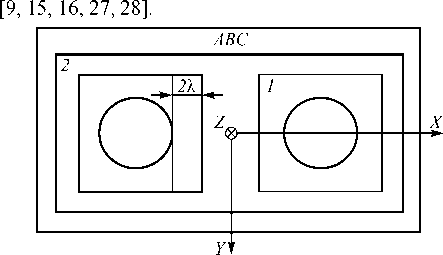
Рис. 1. Схема расчетной области (сечение расчётной 3D-области в координатной плоскости XY)

«Ближняя» зона частицы (область 1, рис. 1) представляет собой параллелепипед, описывающий сферу радиуса R +2λ, где R – радиус наночастицы, λ – длина падающей волны. Размеры «дальней» зоны (область 2, рис. 1) определяются исходя из реализации граничных условий поглощения и представляют собой также параллелепипед с длиной ребра 7 R.

Напряжённость электрического поля, создаваемого электрическим током с амплитудой J imp в области Ω, которая характеризуется электрической ε и магнитной μ постоянными, может быть описана с помощью уравнений Максвелла [3, 5, 16]:

Vx E = -iюцН ;(1)

Vx H = i tosE + Jmp;(2)

• V.(SE ) = - - VJmp;(3)

i to

V■(цH ) = 0,(4)

где E – напряженность электрического поля; H – напряженность магнитного поля; ω – частота источника; i - мнимая единица; V - Гамильтонов (W.R. Hamilton) оператор.

Исследуемая область может быть как двух-, так и трёхмерной. Для определения напряжённости электрического поля E необходимо решить уравнения Максвелла (1)–(4) с учётом граничных условий.

Типовые граничные условия для электрических полей включают однородные условия Дирихле (P.G.L. Dirichlet) на идеально проводящей поверхности, а также смешанные условия на границе поверхности, обладающей волновым сопротивлением. Формулировку этих граничных условий можно записать в виде [15, 16]

n x E = P ; (5)

n x|— Vx E 1 + — n x ( n x E ) = R N , (6)

Ur J П r где n – единичный вектор нормали к границам областей и подобластей; P – установленные значения для компонент поля на ΓD ; ηr – нормальный импеданс поверхности на ΓN ; RN – известные функции, описанные на границе источника.

За счёт исключения напряжённости магнитного поля H в (1) и преобразования (2) можно получить волновое уравнение, называемое уравнением Гельмгольца (H. Helmholtz) [15, 16]:

I 1                   1

Vxl —Vx E I- k 2 s E = - ik₀Z₀ J_m наQ, U r     )                  p

где цT = ц /ц0 и eT = e /e0 - соответственно относитель- ные магнитная и электрическая постоянные;

k 0 = ю^ц ₀ £ ₀ и Z ₀ = ^ц ₀ / s ₀ - волновое число и вол-

Е = ( E x , E y , E z ) = E x i + E y j + E z k .

Будем аппроксимировать на конечном элементе компоненты напряжённости электрического поля следующими вектор-функциями:

^E x ^{( r )} = ^a 0 ^{+ а} 1 r x ^{+ a} 2 ^T y ^{+ a} 3 ^T z ^{+ a} 4 r x r y ^{+ a} 5 r x r z ;

E y ^{( r )} = ^a 6 ^{+ a} 7 r x ^{+ a} 8 r y ^{+ a} 9 r z + a_w T x T y + an r y r ; ⁽⁹⁾

Ez (Г) = ai2 + ai3Tx + ai4Ty + ai5Tz + ai6rxrz + ai7ryr , где r = (rx, ry, rz).

Выражения (9) можно переписать в матричной форме:

Е = [ A ] a ,                                      (i0)

где новое сопротивление (импеданс вакуума).

Используя уравнение (7) и граничные условия (5), (6), можно получить вариационную форму волнового уравнения [15, 16]:

[ A] =

1 r x

0 -

xy

xz

0 -    0

1 rr xy

rrrrr rz rxrz rxrz

J J_ ( v x W ) - ( Vx E ) - k 2 s W ■ E d Q = ^Ц                       J

a ^T = { a ₀ a _i ^   a _i7 } .

Так как (10) справедливо для всего тетраэдра, то

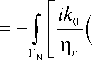
n x

W j ) ( Vx E ) + W j - R N

d r +

для его рёбер будем иметь:

Е e = [ B ] a ,

+ J — ( n x W j ) ( V x E ) d r - ik 0 Z 0 J W j ■ J imp d Q , r D ^Ц r                                 Q

где W j – весовая функция.

2. Рёберный конечный элемент в форме тетраэдра

В силу того, что рассматриваемая область состоит из подобластей (частицы, подложка) с различными значениями ε и μ, на их внутренних границах необходимо выполнение условия непрерывности тангенциальной составляющей полей.

При использовании скалярных узловых конечных элементов [16, 24] выполнить это условие весьма проблематично. Поэтому для решения задачи предлагается использовать рёберные (векторные) конечные элементы (рис. 2) [15].

где E ^e – напряжённость электрического поля на рёбрах конечного элемента, [ B ] – квадратная матрица размерностью 18 на 18, получаемая из матрицы [ A ] последовательной подстановкой координат рёбер (из-за громоздкости здесь не приводится).

Найдём из (11) вектор коэффициентов α :

a = [ B ]^{- 1} E e .

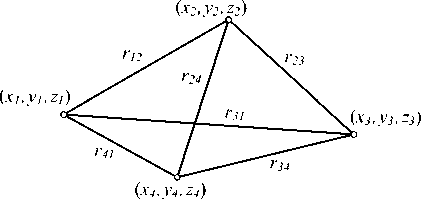
Рис. 2. Векторный конечный элемент в форме тетраэдра

В локальных координатах, специально введённых для конечного элемента, матрица [ B ]^–1 может быть вычислена аналитически. Однако чтобы избежать операции преобразования координат при ассемблировании глобальной матрицы жёсткости, матрица [ B ]^–1 может быть легко вычислена в глобальной системе координат с достаточной для практического применения точностью.

Подставим (12) в (10):

E = [ N e J E e ,                                    (i3)

где

[ N • ]= [ A ][ B ] - ¹,

Вершины конечного элемента имеют координаты ( x i , y i , z i ), где i = 1,4, а рёбра обозначены векторами r lm , где l – номер вершины, из которой выходит ребро, а m – номер вершины, в которое входит ребро.

Представим напряжённость электрического поля в виде:

[ N ^e ] – матрица размерностью 3 на 18, содержащая функции формы в глобальной системе координат конкретного конечного элемента в форме тетраэдра.

Электрическое поле E в области Ω может быть найдено по формуле [15]

N edge             N D

Е = ^ N i E i + £ N D E D , l = i                   l = i

где N edge – число уникальных рёбер в дискретизованной области, исключая те рёбра, которые расположе-

ны на Γ D ; E l – значение электрического поля на l -м ребре; N _l – вектор-функция формы, состоящая из трёх элементов, для l -го ребра; N D – количество рёбер на Γ _D ; N _l ^D и E _l ^D – соответственно векторная базисная функция и значение поля на Γ D .

В качестве весовых функций W j в (8) примем N j :

Wj= N, j = йй..(16)

Подставив (15) и (16) в (8), получим

N edge

Z K mlEl = b m , j = 1, Nedge ,(17)

l = 0

где

^K ml

= J — (VxNm)-(VxNI)-k^rNm • NI dQ + nL^ r_

+ J '(nxNm)(VxNI) dr, Гы L nr_

Г

r

N

N D

Ь m =- Z E ^ - ( VX N m ) ( VX N D ) - k^ r N m • N D ] d- l = 1      - Ц r

- ik 0 Z 0 J N m ■ J imp d n- J N m ■ R „ d F .

После нахождения функций формы по формуле (14) соотношения (17) представляют собой систему линейных алгебраических уравнений, в общем случае сингулярную.

Для избавления от сингулярности требуется произвести учёт граничных условий (5)–(6).

• 3.    Учёт граничных условий

Для учёта граничных условий воспользуемся излучением Зоммерфельда [3, 9, 15, 27]. Предположим, что ограничивающий слой ABC (рис. 1) располагается достаточно далеко от рассеивателя (сфер или других объектов, размещённых внутри ограниченной области), тогда рассеянное поле удовлетворяет соотношению:

n xl ZVx E ^IC L i-k ⁰- n x ( n X E sc ) « 0 ,          (1 8 )

(^r        J П r V где Esc – рассеянное поле, которое является разницей между полным и падающим полями:

E sc = E _— E inc

Тогда (6) примет вид:

n x| ZVx E ^D | + ik ⁰- n x ( n x E ^D ) = U ^inc ,        (19)

(цr J П r где

U ^inc = n xl ZVx E ^inc 1 + ik⁰- n x ( n x E ^inc ) .        (20)

(Ц r          J П r ^v

Теперь, исходя из параметров источника излучения, последовательно вычисляем J imp и E ^inc и подставляем в (20).

Решая задачу (19), находим E ^D .

Полагая R N = U ^inc и используя найденные значения E ^D и условия Дирихле (5), исключаем из (17) известные значения вектора напряжённости E , тем самым в итоге получая систему линейных алгебраических уравнений (17) меньшей размерности и уже с несингулярной матрицей.

Для решения системы уравнений (17) использовался метод сопряжённых градиентов с предобуслав-ливанием Холецкого [29].

• 4.    Верификация предложенной математической модели

Для верификации воспользуемся решением Ми [5] для электрического поля в ближней зоне сферической частицы и решением, полученным с помощью узловых конечных элементов [24].

Рассматривались наночастицы радиусом 40 нм, находящиеся в воздухе (ɛ = 1), их центры совпадают с центром декартовой системы координат. В качестве металлической наночастицы рассматривалась серебряная (Ag) со значением диэлектрической проницаемости материала ɛ_NP = –3,5191 + 0,5798 i .

Для сравнения результатов введём безразмерную величину:

E ^*

E ²

_{E 0} 2 ^,

где E 0 – векторная амплитуда падающей на наночастицу волны.

Для диэлектрической наночастицы выбрано значение ɛ NP = 3,5191 + 0,5798 i .

Для расчёта параметров частиц использовалась модель Друде – Лоренца.

Расчетная область дискретизировалась тетраэдрами для каждой из зон (рис. 1). Граничные условия определялись из решения задачи (19). Результаты расчётов представлены на рис. 3, 4.

Расхождение численного решения согласно предложенной математической модели и решения Ми не превышало 10 %, между интенсивностью элетромаг-нитного поля, найденного с применением скалярных конечных элементов [24], – 15 % (рис. 3, 4).

Таким образом, проведённая верификация показала возможность применения разработанной математической модели для исследования распределения электромагнитного поля в ближней зоне сферических наночастиц.

• 5.    Исследование влияния пары наночастиц на интенсивность электромагнитного поля

Рассматривалась задача определения влияния двух серебрянных наночастиц в золь-гель стекле [2] на электромагнитное поле в ближней зоне.

Возбуждение осуществлялось плоской линейно поляризованной вдоль оси X с длиной волны 405 нм.

Изначально расчётная область была выбрана в форме куба с длиной ребра 5 мкм. В результате она была дискретизирована на 162 миллиона тетраэдров, что привело к матрице системы в (17) размерностью 81812703

неизвестных, решение которой осуществлялось в вычислительном кластере [8] распределенным методом Гаусса с циклическим размещением по строкам.

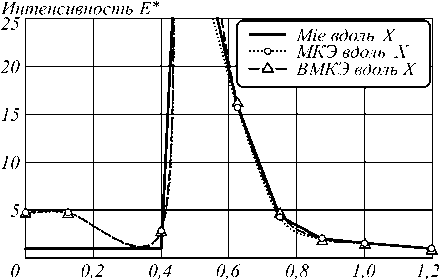
Рис. 3. Зависимость интенсивности электромагнитного поля в ближней зоне от расстояния от центра металлической наночастицы вдоль оси X (10-7м)

В ходе проводимых вычислительных экспериментов размер расчётной области уменьшался до тех пор, пока получаемые результаты не отличались от первоначальных не более, чем на 10%.

В конечном итоге было получено, что расчётная область может быть выбрана в форме параллелепипеда размерами 2500×1250×1250 нм. Дискретизация проводилась конечными элементами различных размеров в зависимости от зоны (рис. 1). Количество уз- лов в этом случае составило 508032. После учёта граничных условий размерность матрицы системы (17) в проводимом исследовании не превышала одного миллиона неизвестных. Для решения использовался метод сопряжённых градиентов с предобуславлива-нием Холецкого [29].

Результаты моделирования представлены на рис. 5. Для сравнения на графиках приведены значения интенсивности E ^*, полученные для одной наночастицы согласно теории Ми.

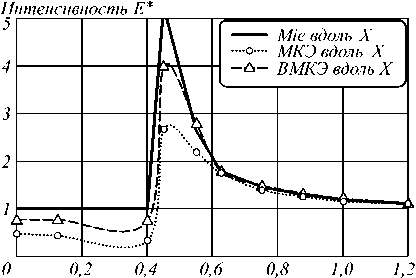
Рис. 4. Зависимость интенсивности электромагнитного поля в ближней зоне от расстояния от центра диэлектрической наночастицы вдоль оси X (10 –7м)

Интенсивность Е*

г) -1,85    -1,11     -0,37     0,37     1,11     1,85

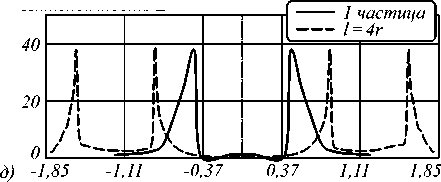
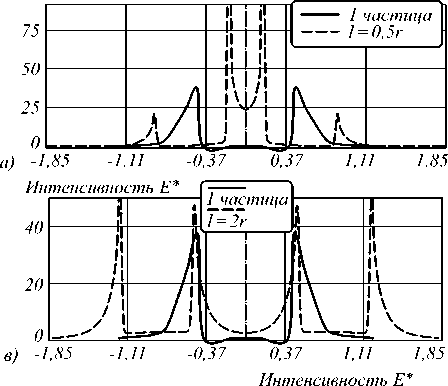
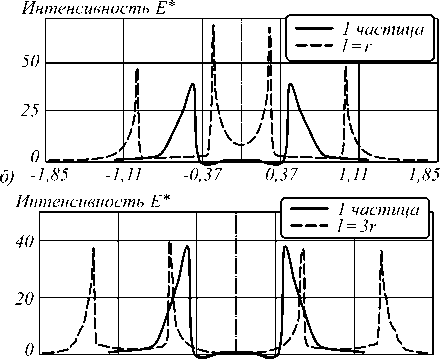
Рис. 5. Зависимость интенсивности электромагнитного поля в ближней зоне двух наночастиц в зависимости от расстояния между ними вдоль оси X (10 –7м): расстояние равно половине радиуса частицы (а); радиусу (б); двум радиусам (в); трём (г); четырём (д)

Заключение

Предложенные функции формы и алгоритм построения системы (17) позволяют найти распределение электромагнитного поля, обеспечивая непрерывность его тангенциальной компоненты при переходе между границами конечных элементов. Это позволяет вычислять распределение полей в ближней зоне наночастиц, где интенсивность E* принимает значительные значения, приводящие к переполнению вещественных типов данных при использовании других методов. Кроме того, становится возможным использовать нерегулярный шаг сетки, увеличивая размер конечных элементов в «дальней» зоне, что приводит к снижению размерности задачи и уменьшению времени нахождения решения. При этом можно моделировать не только наночастицы сферической формы, но и любой произвольной, дискретизируя их совокупностью разноразмерных тетраэдров. Таким образом, появляется возможность учёта наличия выщербин, «пещер» и полостей у наночастиц.

В ходе вычислительного эксперимента был определён размер расчётной области, обеспечивающий минимальное число узлов конечно-элементной сетки. Выделены «ближняя» и «дальняя» зона частицы (рис. 1), представляющие собой кубы с длиной ребра соответственно R +2λ и 8 R +2λ. При этом при дискретизации «дальней» зоны возможно использовать конечные элементы в 2 раза большего размера, чем при дискретизации «ближней». Это позволит значительно снизить размерность получаемой системы алгебраических уравнений (17).

При исследовании влияния расположения пары наночастиц на интенсивность электромагнитного поля расстояние между частицами варьировалось от 0,5 радиуса частицы (20 нм) до 10. Численные результаты показали, что при расстоянии между частицами свыше 4 радиусов влияние на электромагнитное поле практически отсутствует, а значение интенсивности сопоставимо с интенсивностью электромагнитного поля одной частицы.