Численное моделирование волны пластичности при высоких скоростях нагружения как результата множественных неравновесных структурно-кинетических переходов
Автор: Соковиков М.А.
Рубрика: Применение общей термодинамической теории к решению проблем механики
Статья в выпуске: 13, 2005 года.
Бесплатный доступ
Изучалась волновая природа пластического деформирования при ударном нагружении. Волна пластичности обусловлена последовательным распространением неравновесного структурно-кинетического перехода в системе микросдвигов от сечения к сечению образца и движется со своей собственной скоростью, отличной от скорости волн напряжений. Показано, что волны пластичности обладают солитоноподобными свойствами: скорость их распространения существенно зависит от амплитуды.
Короткий адрес: https://sciup.org/146211268
IDR: 146211268 | УДК: 539.42
Текст научной статьи Численное моделирование волны пластичности при высоких скоростях нагружения как результата множественных неравновесных структурно-кинетических переходов
Исследования, приведенные в [1–6], указывают на волновую природу пластической деформации.
Многочисленными экспериментальными исследованиями показано, что важными дефектами структуры, определяющими релаксационные свойства и кинетику разрушения реальных материалов, являются микросдвиги, микротрещины – типичные дефекты мезоуровня [7–12]. Так, многочисленные структурные исследования процессов нагружения с различными скоростями указывают на определяющую роль в явлениях пластического деформирования согласованного поведения ансамбля этих микродефектов. В данном исследовании построена математическая модель, описывающая волновой характер пластического деформирования при высокоскоростном нагружении с учетом нелинейного поведения ансамбля взаимодействующих микросдвигов.
Значительное внимание вопросам природы пластической деформации уделено в работах [13–15], где развивается представление о деформируемом твердом теле как о многоуровневой системе, в которой пластическое течение развивается как последовательная эволюция потери сдвиговой устойчивости на различных масштабных уровнях: микро, мезо и макро.
Обсуждаемый класс явлений в последние годы исследуется нелинейной физикой [16, 17], рассматривающей данные эффекты с позиций неравновесных структурнокинетических переходов.
В данной работе используется ранее разработанная теория [16], в которой методами статистической физики и термодинамики необратимых процессов изучается влияние микросдвигов на упругие и релаксационные свойства твердых тел. Определяющие уравнения сред с микросдвигами имеют следующий вид:
σ ik = L 1 e i p k - L 2 p & ik , Π ik = L 2 e i p k - L 3 p & ik , (1)
где pik – тензор, характеризующий интенсивность и преимущественную ориентацию микросдвигов; Π ik =∂ F – термодинамическая сила, действующая на систему, когда
∂ pik
Применение общей термодинамической теории к решению проблем механики pik отличается от равновесного (F – свободная энергия среды с микросдвигами); cik, epk - тензоры напряжений и скоростей пластических деформаций; Li -кинетические коэффициенты, зависящие от pik . Определяющие уравнения материала (1) включают соотношения релаксационного типа для тензора напряжений и уравнения движения для параметра pik . В этих уравнениях учтены «перекрестные» эффекты:
влияние микросдвигов на релаксационные процессы и пластичности на кинетику роста pik . В дальнейшем рассматривается случай, когда пластическая деформация подчиняется условию е^ = 0 (пластическая несжимаемость материала), а среднее напряжение c = 3 cii определяется через упругие составляющие тензора деформации.
В рамках данной теории были определены характерные реакции материалов на образование дефектов.
Рассматривается цилиндрический образец армко-железа, нагружаемый налетанием длинного ударника, в ходе которого реализуется одномерное напряженное состояние, су ^ 0, су = су = 0. zz , xx yy .
Используя представление о малости деформаций и скоростей деформаций, для упругопластической среды имеем
где & zz , s Zz , & p zz - скорости суммарной, упругой, пластической деформации.
Для одномерного напряженного состояния получаем следующую формулировку закона Гука в переменных полной и пластической деформации:
zz zz zz , или в типичном для динамических постановок представлении
( da p
dt где vz – скорость по z .
Запишем уравнение движения для случая одномерного напряженного состояния, d vzdc p —z_ _ —zz, dt
вводим удельный объем
V = Po/P, где p0 - начальное значение плотности, p - текущее значение плотности, Используя уравнения (4), (5), (7), запишем
P 0 d v z = dc zz
V 61 dz ’
S2 zL _ E v z _ & p 1
dt (dz zz)
Применение общей термодинамической теории к решению проблем механики
Для пластической составляющей тензора скоростей деформации существенна девиаторная компонента тензора напряжений g' - Gz,(10)
zz 3 zz с учетом которой релаксационные уравнения, описывающие упруго–пластические свойства среды с дефектами имеют вид g' = l £P7 - L ,(11)
zz 1zz 2, d t nzz= 12£pz -13 — ,(1-)
zz 2 zz 3
8 t
Динамическое воздействие на стержень описывается граничным условием
Gzz (0, t) = Go - f (t),(13)
где f ( t ) функция, описывающая импульс нагрузки формы, близкой к прямоугольной, длина которого существенно превышает диаметр образца.
Тыльная сторона стержня свободна от нагрузки
Gzz (l, t) = 0.(14)
Система должна удовлетворять начальным условиям
Vz (z ,0) = G zz (z ,0) = Pzz (z ,0) = 0,(15)
V p (0, t ) = 0 ; V p ( 1 , t ) = 0 , z G [0,1], t G [0, to ) .
Здесь p - плотность материала; t - время; z - пространственная координата; v z
- компонента вектора скорости; gzz, g'zz , £p:, pzz - компоненты тензоров напряжений, девиатора напряжений, скоростей пластических деформаций, параметра плотности микросдвигов; E – модуль Юнга, l– длина стержня,. l1,l2,l3 – кинетические коэффициенты, Пzz =---, где F - свободная энергия.
dPzz g — t zz , t = —
G A t
Обезразмерим систему (8)- (15). Введем безразмерные параметры gzz z V 1
где Д t = 1 1 / G , z = —, где l - длина стержня, v = ""zj^G; ’ П zz = .
Получаем систему уравнений в безразмерном виде
dv dGzz— = a V—zz dt 5z
8g zz E (8v - )
zz
,
8 1 G\8z p )
-
• —f
£ p = Gzz +
-
l - 8 p z^
11 81
dP zz = 4 £ d T 1 3 p
-П',
G zz = G zz + G ,
l 2 l
где a = —1—z-, П = At - П = — П = \П .
zz zz 1 zz p0 Gh G
Применение общей термодинамической теории к решению проблем механики
В аппроксимацию функции Π′ , отвечающей за генерацию микросдвигов, введен член, описывающий нелокальность, который учитывает распространение волн пластической деформации в пространстве.
Π′=- A 2 ⋅σ′ zz ⋅ exp( - p a / p zz ) + B 1 ( p zz - p b ) - D 1 ∂ p 2 zz , (21)
∂z где A,B,pa,pb – параметры аппроксимации, A2= A1(p/p*)4 ; p∗ – некоторая константа; D1 – коэффициент нелокальности.
При этом метастабильная ветвь реакции материала на образование микросдвигов реализуется при достижении определенного уровня дефектности материала. Функция A 2 = A 1( p / p *)4 учитывает качественное изменение реакции твердого тела на образование микросдвигов в зависимости от дефектности структуры.
Численное исследование системы (16) – (21) проводилось методом конечных разностей.
Использовались следующие значения констант для армко-железа ρ= 7.8 ⋅ 103кг/м3, E = 20.6 ⋅ 1011Па, G = 0.8 ⋅ 1011Па, l 1 = 1.0 ⋅ 105н с, l 2 = 0.45 ⋅ 105н с, l 3 = 1.0 ⋅ 105н с,
A = 57.0, B = 0.25 ⋅ 10 - 2 ⋅ A , p a =- 1.5 ⋅ 10 - 3, p b =- 1.5 ⋅ 10 - 4.
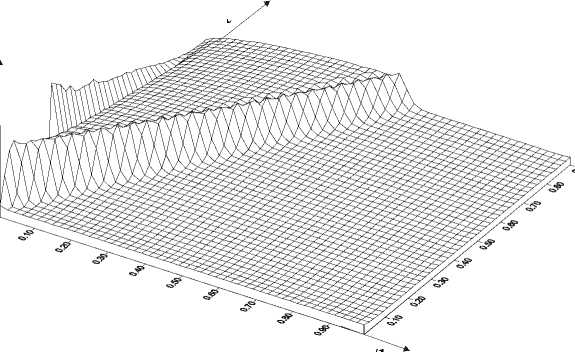
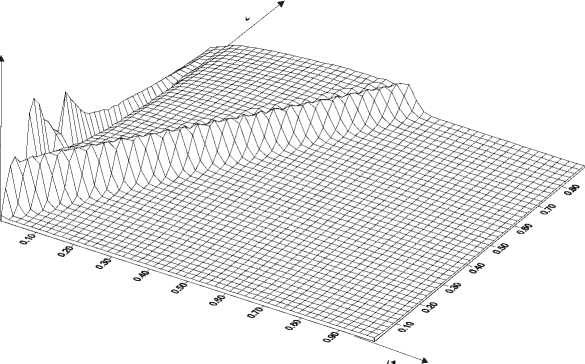
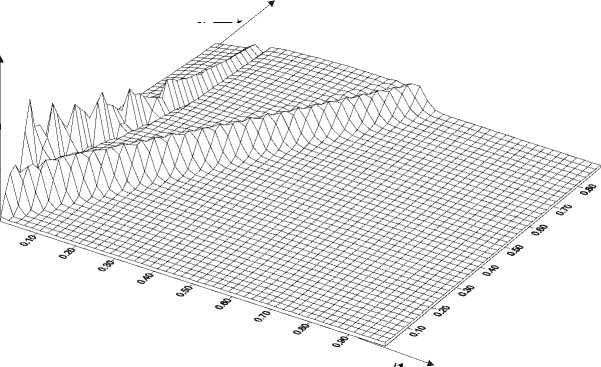
В результате численного моделирования получено, что структурнокинетический переход по параметру плотности микросдвигов распространяется от сечения к сечению стержня с некоторой скоростью и, как следствие, распространяется скачок скоростей пластических деформаций. Релаксация напряжений происходит последовательно в каждом сечении образца. При этом, распространение пластической деформации вдоль по длине образца можно рассматривать как своеобразную пластическую волну, имеющую свойства уединенной волны, в частности, имеет место сильная зависимость скорости пластической волны от амплитуды. Результаты численного моделирования представлены на рис.1 – 3. Наблюдается увеличение скорости пластической волны с ростом величины импульса напряжений. При небольших амплитудах нагружающего импульса волна пластичности затухает, пройдя небольшое расстояние. С ростом амплитуды глубина проникновения волны пластичности по длине образца увеличивается. Учет нелокальности позволяет описать формирование специфической волны пластических деформаций, природа которой обусловлена неоднородностью пластического течения, постепенным распространением пластических деформаций от мест с большей концентрацией микронапряжений по объему образца [1]. В данном случае имеет место формирование и распространение со своей специфической скоростью волн пластической деформации. Волны пластичности, обнаруженные экспериментально при квазистатическом нагружении, описаны в [1–3]. Многочисленные исследования [18,19] указывают на общность релаксационных механизмов при статическом и динамическом нагружении. Поэтому существование специфических волн пластичности при высокоскоростном динамическом нагружении представляется весьма вероятным.
Высокие скорости деформаций могут привести к усилению неравновесности в системе дефектов и, как следствие, к новым нелинейным закономерностям деформационного поведения материалов, связанным с немонотонным характером изменения релаксационных свойств в процессе высокоскоростного нагружения.
Исследования, приведенные в [3], указывают на волновую природу пластической деформации. Волны пластичности могут быть описаны уравнениями,
Применение общей термодинамической теории к решению проблем механики имеющими существенно нелинейный характер, позволяющий описать свойства уединенной волны, проявляющиеся при распространении пластической деформации.
t/At
■
I
V#
z/l
■
■
I
a t/At
^
z/l
б
t/ A t
/
/
z/l
в
Рис.1. Распространение волны пластичности по длине стержня при амплитуде импулься: a) 6 0 = 0.033 ; б) 6 0 = 0.045 ; в) 6 0 = 0.058 A t -характерное время, l – длина стержня, G – модуль сдвига
■
Применение общей термодинамической теории к решению проблем механики t/At
■
z/l
t/At
z/l
б
t/At
■
Ip
z/l
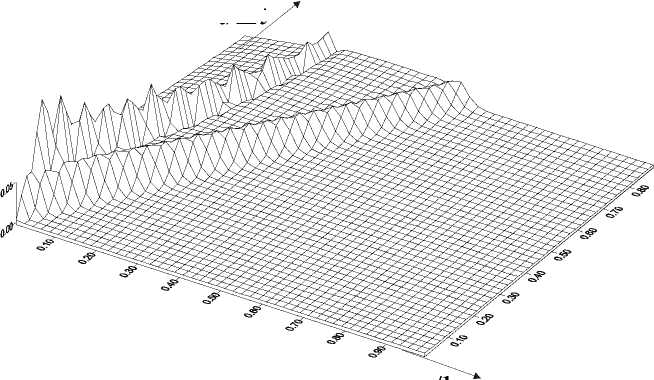
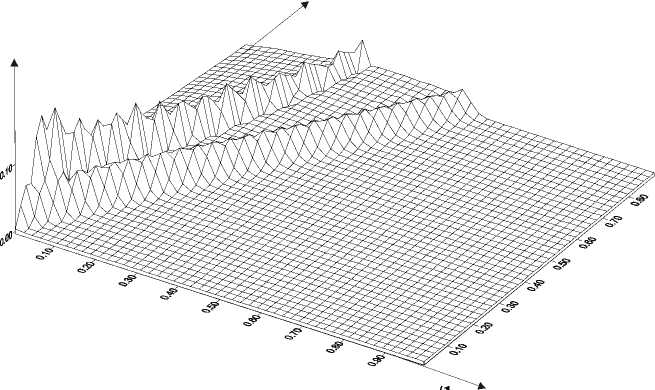
Рис.2. Распространение амплитуде импулься: a)
в волны пластичности по длине стержня при
50 = 0.070; б) 50 = 0.083; в) 50 = 0.095 At - характерное время, l – длина стержня, G – модуль сдвига
'
O ZZ / G
Применение общей термодинамической теории к решению проблем механики t/At
/
z/l
a
t/At e.»1'
p zz
z/l
б
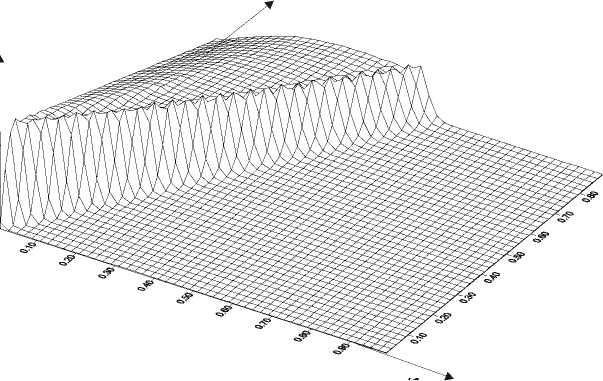
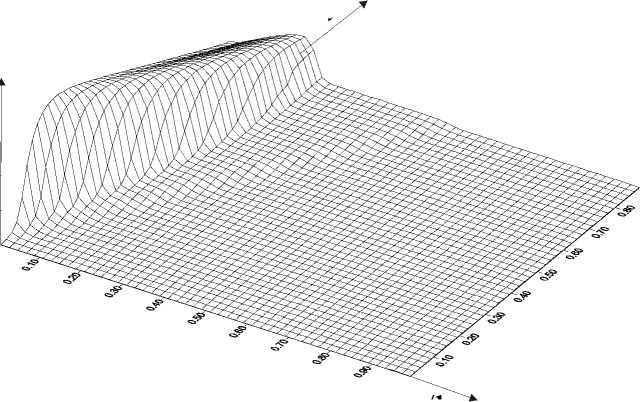
Рис.3. Распространение волны пластичности по длине стержня при амплитуде импулься O 0 = 0.070: a) девиаторная компонента O'zz , б) p zz -компонента тензора плотности микросдвигов; A t - характерное время, l -длина стержня, G – модуль сдвига
Существенная нелинейность уравнений является отражением глубинных свойств процессов, происходящих в структуре деформируемого материала, и естественно связана с существенно нелинейной кинетикой развития ансамблей микродефектов. В процессе распространения волн пластичности происходят множественные неравновесные кинетические переходы по параметру плотности микросдвигов, сопровождающиеся скачкообразным уменьшением времен релаксации и соответственно резким ростом скоростей пластических деформаций.
Исследования проводились при частичной поддержке грантов РФФИ № 02-0100736, № 04-01-96042.
Применение общей термодинамической теории к решению проблем механики


