Численное моделирование заполнения микропор методом функции распределения

В настоящее время задачи моделирования поведения частиц вблизи ограничивающих поверхностей в физике наноматериалов и наноструктур приобрели дополнительную актуальность. Многие современные методы исследования материалов были разработаны еще до появления наноструктур. Их применение к интерпретации экспериментальных результатов вызывает сложности, в частности при определении удельной поверхности в микропористых и супермикропористых наноструктурах. Также не всегда оказывается возможным непосредственно учесть ряд факторов, что делает восстановление некоторых микроскопических характеристик вещества неоднозначной обратной задачей. Подобные проблемы можно устранить посредством прямого моделирования структуры газа или жидкости в ограниченном объеме, с учетом геометрии ограничивающих поверхностей и вида межмолекулярного взаимодействия молекул адсорбента со стенкой или стенками.

Для этой задачи необходимо рассчитать напрямую потенциал адсорбционного взаимодействия на основе суммирования парных потенциалов. В конечном итоге это путь сочетания обычного физикохимического эксперимента с численным экспериментом, который проводится на ЭВМ. Подобный подход позволяет выявить особенности поведения адсорбирующегося газа (жидкости) для конкретной системы микропор довольно точно, при этом явно выделить эффект размеров системы и характера межмолекулярного потенциала взаимодействия. Это позволяет повысить надежность обработки экспериментальных результатов, работать с отдельными массивами данных, конструируя их из поведения отдельных микропор. На результаты физических экспериментов практически всегда влияют дополнительные неучтенные параметры, погрешности приборов, неоднородность используемых образцов и т.д. В численном эксперименте все эти дополнительные помехи отсутствуют. Правда, вместо них возникают чисто вычислительные проблемы сходимости, множественности решений и поиска глобального минимума многоэкстремальных функций и т.д., но все эти проблемы решаются методами вычислительной математики, которые быстро совершенствуются.

В рамках реализации данного подхода была написана программа расчета одночастичной функции распределения, зная которую, можно рассчитать макроскопические характеристики молекулярной системы. Исходная система уравнений Орнштейна-Цернике, выбор замыкания для задачи моделирования свойств газов (жидкостей средней плотности) в ограниченных объемах описаны в публикациях [1-4]. Данная программа написана на языке Питон и предназначена для работы в первую очередь под операционной системой Линукс, хотя и может использоваться под операционной системой семейства Windows. Для установки программы необходимо иметь компьютер, работающий под операционной системой Линукс, после чего требуется проверить наличие следующих библиотек и модулей:

• •    Интерпретатор языка Питон;

• •    Библиотека языка СИ fftw3;

• •    Библиотека языка Питон numpy;

• •    Библиотека языка Питон scipy;

• •    Библиотека pyQt4.

В частности, при использовании дистрибутива Debian Linux Leny можно применить популярную утилиту apt-get. Библиотека языка СИ fftw3 используется для вызова быстрого преобразования Фурье. Библиотека языка Питон numpy – для эффективной работы с массивами. Библиотека языка Питон scipy – для интерполяции функций, чтобы избежать проблем с областью применимости функций. Библиотека pyQt4 – для организации графического интерфейса работы с программой. Все остальные функции программы, реализованы штатными средствами языков Питон и СИ. Данный подход позволил сделать программу достаточно простой и удобной для дальнейшей модификации. Важно, что программа использует только свободное программное обеспечение и поэтому является «лицензионно чистой». Это позволит использовать ее в процессе обучения студентов и аспирантов, изучающих спецкурсы, связанные с физикой жидкостей и нанотехнологиями.

Программа разбита на два модуля, каждый из которых организован в виде отдельного каталога. Первый каталог называется 0.003, второй называется 0.012. Подобная организация каталогов вызвана логической необходимостью разделить задачу на две части для нахождения сферически-симметричного решения, двухчастичной функции распределения и вычисления одночастичной функции распределения вблизи ограничивающих поверхностей в синглетном приближении.

Результат вычисления первой программы используется при работе второй, хотя сами вычислительные процедуры организованны независимо. Результат работы первой программы передается в виде файла w12.txt, который формируется в каталоге 0.003 после запуска программы вычисления объемного решения двухчастичной функции распределения.

Обе программы предусматривают работу как в консольном режиме, так и с использованием графического интерфейса. Перейдем к описанию работы с программой вычисления двухчастичной функции распределения. При работе в консольном режиме необходимо вызвать терминал и перейти в рабочий каталог. После чего запускается файл fftw3-proba, этот файл считывает данные из файла w12.cfg, который содержит все параметры необходимые для расчета.

При работе с использованием графического интерфейса, необходимо из рабочей директории запустить файл 1-002.py; в результате мы увидим окно программы, представленное на рис. 1. Это графический интерфейс для расчета двухчастичной функции распределения. На рис. 1 мы видим графический интерфейс программы расчета одночастичной функции распределения, в данном случае показан пример расчета вблизи ограничивающей поверхности. Интерфейс состоит из трех областей, в левом верхнем углу находится окно параметров, которые можно изменять, под ним находятся кнопки: «принять», «сохранить», «запустить». При нажатии кнопки «сохранить» программа записывает параметры, отображаемые в окне, в конфигурационный файл, при нажатии кнопки «запустить» она сохраняет параметры в файл и после этого вызывает программу, которая читает данные из этого файла.

Справа вверху находится окно, отображающее график получаемой функции, справа внизу под ним – визуализация расчета точности получаемого решения (рис. 2). Это достигается выводом в виде графика значения погрешности расчета для каждой точки. Данная опция позволяет контролировать сходимость решения и является весьма важной.

В строке 1 отображается «число параметров», эта строка предусмотрена для дальнейшего возможного расширения функциональности программы в будущем. В строке «файл конфигурации» указывается имя файла, в котором хранятся все параметры и который можно использовать при запуске в консольном режиме. В строке «потенциал 1-LJ, 2-HS, 3-user» отображается возможность задать числом тип используемого при расчете потенциала межмолекулярного взаимодействия. Задав «тип 1», мы будем вести расчет с потенциалом Леннарда-Джонса, задав «тип 2», мы будем работать с потенциалом твердых сфер.

В строке «максимальный радиус» речь идет об учете эффективного радиуса учитываемых корреляций. Строка «количество интервалов разбиения» задает масштабную сетку для работы алгоритма; по сути, речь идет о количестве узлов, которые используются при вычислении интегралов. Строка «обратная температура» характеризуют глубину «ямы» в потенциале Леннарда-Джонса и не исполь- зуется при вычислениях с потенциалом твердых сфер; в этом случае данный параметр просто игнорируется программой.

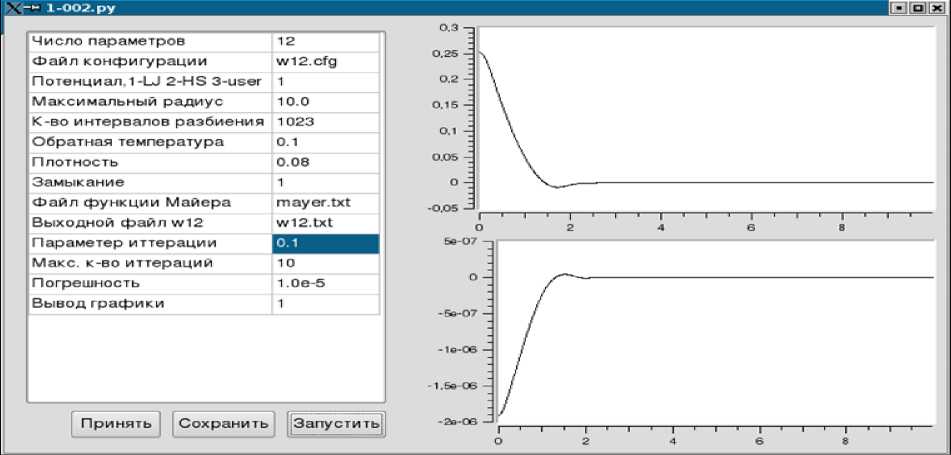
Рис. 1. Графический интерфейс программы расчета двухчастичной функции распределения

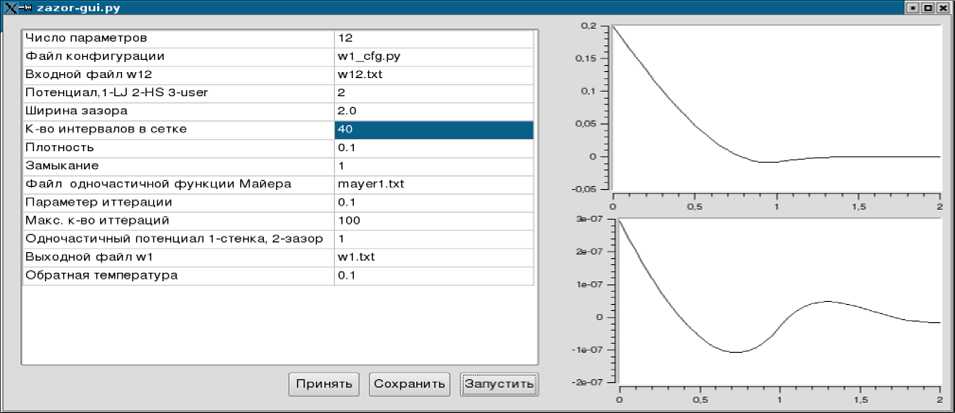
Рис. 2. Графический интерфейс программы расчета одночастичной функции распределения вблизи твердой стенки

Строка «плотность» задает безразмерную приведенную концентрацию газа. Строка «замыкание» позволяет выбирать тип замыкания; по умолчанию стоит единица и в этом случае программа работает с гиперцепным замыканием. Строка «Файл функции Майера» – это название файла, в котором лежит файл отвечающей майеровской функции внешнего поля. В случае расчета сферически-симметричного двухчастичного решения этот файл состоит из нулей, что соответствует внешнему однородному полю. Строка «Выходной файл» отвечает названию файла, который будет содержать результирующий массив значений функции при заданных условиях. Строка «Параметр итерации» представляет собой числовое значение, которое является внутренней переменной программы, отвечающей за критерий точности при сходимости решения. Чем выше плотности, тем меньше должен быть этот параметр. Соответственно чем больше этот параметр, тем выше быстродействие программы, но меньше точность. Обычно его значения можно задавать в интервале от 0,005 до 0,1 и этого будет достаточно. Строка «Максимальное количество итераций» также отвечает внутренней переменной и нужна для контроля точности и сходимости решения. Строка «погрешность» дает критерий погрешности, при достижении которого программа останавливает расчет. Строка «вывод графики»

позволяет включить и отключить прорисовку графиков. При значении ключа 1 графики строятся; при значении ключа 0 графики не строятся.

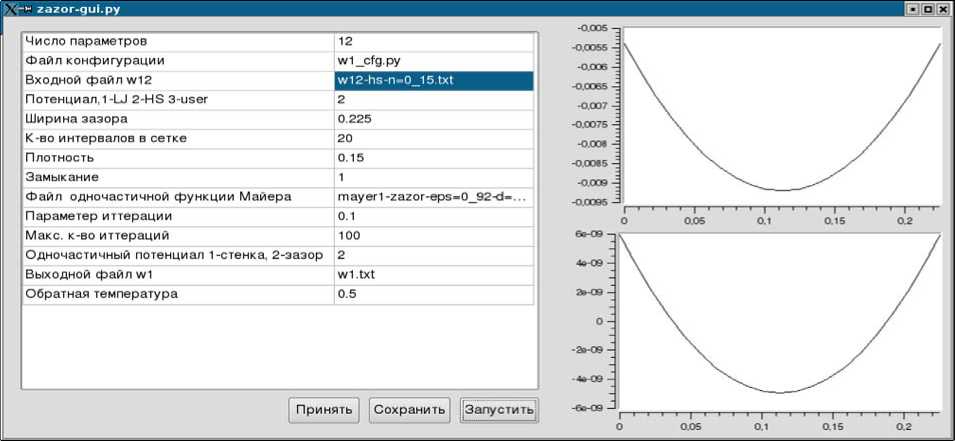
Рис. 3. Графический интерфейс программы расчета одночастичной функции распределения в плоском зазоре

В правом верхнем окне выводится график, который отображает результат расчета функции с заданными условиями. В правом нижнем окне выводится график, показывающий погрешность расчета. После копирования файла w12.txt в каталог 0.012 можно переходить к расчету одночастичной функции распределения. Для устойчивой работы программы рекомендуется учитывать следующие факторы. Вначале всегда необходимо рассчитать двухчастичную функцию распределения, а затем рассчитывать все требуемые одночастичные функции распределения с такими же потенциалом взаимодействия, приведенной плотностью и обратной температурой.

Выбор замыкания для решения при малых плотностях не является существенным вопросом, так как все корректные замыкания при малых плотностях дают одинаковую точность. При более высоких плотностях, начиная с приведенной концентрации 0,6, расхождение между различными замыканиями становится существенным. В этом случае наиболее последовательные результаты дает гиперцепное замыкание, которое используется в программе по умолчанию. Однако есть возможность использовать другие замыкания, чтобы решать задачу о сходимости уравнений с различными замыканиями.

При работе с потенциалом твердых сфер необходимо задав приведенную плотность, проверить строки «максимальный радиус», «Параметр итерации», «Максимальное количество итераций». Строка «максимальный радиус» для однородной жидкости должна задаваться не менее 10, по сути, эта строка отображает расстояние, на котором еще учитываются корреляции между частицами; расстояние выражено в диаметрах частицы. Если задать это значение меньше 10, то программа может начать существенно, медленнее сходиться к правильному решению. Параметры итерации также следует подбирать в зависимости от плотности. При повышении плотности, с которой начинается расчет, нужно уменьшать значение в строке «параметр итераций». Правильность задания параметров можно контролировать по нижнему графику. На нем откладывается разница между двумя последними итерациями каждой точки при расчете. Чтобы получить оценку погрешности расчета сверху, необходимо поделить на параметр итераций и умножить на десять. Строка «максимальное количество итераций» необходима для того, чтобы подробно контролировать сходимость решения. При увеличении «максимального количества итераций» возможен более подробный визуальный контроль за сходимостью решения (рис. 3).

При работе с потенциалом Ленарда-Джонса, если наблюдается расходимость, то необходимо сначала повышать температуру, чтобы попасть в область эффективного отталкивания при высоких температурах, и потом делать небольшие итерации по температуре в обратном направлении. В результате можно получить сходимость даже при достаточно высоких плотностях.

При расчете одночастичной функции распределения надо учитывать, что потенциал взаимодействия со стенкой (стенками) всегда задается так, что его крайние значения – это предельные значения потенциала. Таким образом, не возникает вопрос о расходимости решения. Кроме того, следует помнить, что потенциал необходимо перевести в вид, соответствующий функции Майера, и записать в виде файла, который указывается в программе как параметр. Программа позволяет решать ряд задач статистической физики жидкости (расчет локальной плотности, структуры ближнего порядка), так и для разработки рекомендаций по совершенствованию методов обработки термодесорбционного эксперимента, в частности, по измерению удельной поверхности, линейной термопрограммируемой десорбции. Программа может быть использована при изучении студентами курса статистической физики жидкостей, физики конденсированного состояния и в качестве лабораторной работы по численному эксперименту. Наглядная оболочка позволяет решать все вышеперечисленные задачи, а хорошо верифицированный алгоритм счета является надежной основой для дальнейшей работы [5-8].

Моделирование принципиально не ограничено числом взаимодействующих частиц, как в методах молекулярной динамики [9] (учитывается естественным ходом убывания парных функций распределения с расстоянием), размерами и формой пор, гетерогенным составом поверхности, особенностями межмолекулярного взаимодействия, числом адсорбирующихся компонентов и т.д. Любые усложнения модели ограничены лишь мощностью используемых компьютеров, которые непрерывно совершенствуются. Дальнейшее развитие программного комплекса мы видим в написании модуля, обрабатывающего темодесорбционные измерения и в более тесной интеграции модулей, отвечающих за расчет адсорбционных величин из первых принципов и обработку эксперимента. Одновременно данный программный комплекс может быть применен с учетом необходимой для этого термодинамики к расчетам транспорта разнообразных молекул через различные пористые среды, поведения смесей флюидов, исследования фазовых переходов в ходе адсорбции на наноструктурированных поверхностях. Очевидно, что за такими подходами – огромное будущее и они рано или поздно заменят традиционные подходы.